Треугольник АВС равнобедренный , стороны равны 5 5 и 4
треугольник DEF ортотреугольник, то есть образован пересечениями всех трех высот , тогда найдем длин каждой стороны!
Найдем с начало длину АЕ , высоту проведенной к боковой стороне, так как площадь треугольника равна S=ah/2 ; то найдем площадь треугольника зная основание и потом высоту, и выразим через другую сторону высоту
BF = √5^2-2^2 = √21
тогда с одной стороны S=2√21 , с другой
S=5*AE/2
AE= .
так как наш треугольник равнобедренный то высоты проведенные к боковым сторонам равны AE=CD
Найдем теперь стороны нашего ортотреугольника
для это найдем угол ABC
по теореме косинусов
BE=BC-EC
EC=√AC^2-AE^2 =
BE=5-1.6=3.4
по теореме косинусов
DE=
DF=
значит EF=2
и того P=2+2+2.72= 6.72
Презентация на тему: Ортотреугольник и его свойства
Муниципальное общеобразовательное учреждение«Лицей № 230» Ортотреугольники его свойства Работу выполнилаученица 9 «А» класса МОУ «Лицей» № 230Волкова Екатерина Евгеньевна.Руководитель:Редкина Елена Ивановна г.Заречный, Пензенская область2008 г.
Италия, начало XVIII века Инженер и математик Фаньяно Дей Тоски (1682—1766) Задача: вписать в данный остроугольный треугольник ABC треугольник наименьшего периметра так, чтобы на каждой стороне треугольника ABC лежала одна вершина треугольника. Существует единственный вписанный треугольник наименьшего периметра – ортотреугольник.
Цель данной работы:описание дополнительных геометрических свойств треугольника. Задачи:1) выяснить, что такое ортотреугольник;2) изучить его свойства;3) рассмотреть возможное применение этих свойств к решению задач.
Свойства ортотреугольника Ортотреугольник отсекает треугольники, подобные данному.Две смежные стороны ортотреугольника образуют равные углы с соответствующей стороной исходного треугольника.3. Высоты треугольника являются биссектрисами ортотреугольника. 4. Ортотреугольник – это треугольник с наименьшим периметром, который можно вписать в этот треугольник .5. Периметр ортотреугольника равен удвоенному произведению высоты треугольника на синус угла, из которого она исходит.
2.1 Теорема о подобии треугольников Ортотреугольник отсекает треугольники, подобные данному.
2.2 Теорема о свойстве биссектрис ортотреугольника
2.3 Теорема Фаньяно Среди всех треугольников, вписанных в данный остроугольный треугольник, наименьший периметр имеет ортотреугольник.
2.4 Физический смысл и механическая модель задачи Фаньяно
2.5 Периметр ортотреугольника
Задача 1. Пусть и – высоты треугольника АВС. Докажите, что треугольник подобен треугольнику АВС. Чему равен коэффициент подобия?
Задача 3. В остроугольном треугольнике АВС проведены высоты АD, ВЕ и СF.Докажите, что pR=Pr, где p-периметр треугольника EDF, Р – периметр треугольника АВС.
Задача 5. В равнобедренном треугольнике ABC с основанием AC = 4 и боковой стороной AB = 8 проведены высоты . Найти периметр треугольника и длину высоты .
Периметр ортотреугольника равнобедренного треугольника
Предметом нашего исследования являются ортоцентрические треугольники и их свойства.
Цель – изучение свойств ортоцентрических треугольников и исследование путей их использования для решения задач.
1) выяснить, что такое ортотреугольник;
2) изучить и проанализировать свойства ортотреугольников;
3) рассмотреть возможное применение
этих свойств для решения задач.
4) подвести итоги.
Во время выполнения поставленных задач нами был использован описательный метод исследования, изучение и обобщение.
Практическая значимость: результаты проведенного исследования могут стать опорой для решения олимпиадных задач, задач ЕГЭ и ОГЭ с использованием свойств отроцентрических треугольников.
Глава 1. Исторические сведения и свойства
§ 1. Что такое ортоцентрический треугольник?
Ортотреуго́льник (ортоцентрический треугольник) — это треугольник ΔA1B1C1, вершины которого являются основаниями высот треугольника ∆ABC. Для ортотреуго́льника (для ортоцентрического треугольника) ΔA1B1C1 сам треугольник ∆ABC является треугольником трёх внешних биссектрис. То есть отрезки AB, BC и CA являются тремя внешними биссектрисами треугольника ΔA1B1C1.
§ 2. Исторические сведения
В начале 18 века итальянский инженер и математик Фаньяно дей Тоски поставил перед собой такую задачу: вписать в остроугольный треугольник АВС треугольник наименьшего периметра так, чтобы на каждой из сторон данного треугольника лежала одна вершина вписанного. Аналитическое решение этой задачи было опубликовано в 1755 году. Было доказано, что существует единственный треугольник наименьшего периметра KMN, его вершина K – основание высоты CK. Искомым треугольником всегда будет ортотреугольник KMN.
§ 3.Свойства ортотреугольников
1.Теорема о подобии треугольников. Ортотреугольник отсекает треугольники, подобные данному.
В остроугольном треугольнике проведены высоты , . Найдем углы треугольника , если , а .
Прямоугольные треугольники и имеют общий угол при вершине С, они подобны, поэтому .
Из этого равенства следует, что в треугольниках и стороны, прилежащие к общему углу при вершине С, пропорциональны. Следовательно, по второму признаку подобия треугольников подобен . В подобных треугольниках против соответственных сторон лежат равные углы, поэтому угол , .
Аналогично можно доказать подобие треугольников и ; и , если провести высоту CC1. При этом , и .
Как следствие данной теоремы, верно следующее утверждение:
Две смежные стороны ортотреугольника образуют равные углы с соответствующей стороной исходного треугольника.
Среди всех треугольников, вписанных в данный треугольник, только ортотреугольник обладает указанным свойством.
І. Ортоцентрический треугольник H1H2H3 В остроугольном треугольнике ABC соединим отрезками основания высот H1,H2,H3 (рис. 1). Получим
треугольник H1H2H3. Рассмотрим некоторые свойства этого треугольника, которые используют при решении задач.
Свойство 1. Стороны ортоцентрического треугольника H1H2H3 антипараллельны сторонам треугольника ABC.
Доказательство. Обозначим точку H — точку пересечения высот треугольника ABC (ортоцентр). Опишем окружность около четырёхугольника AH2HH3. Тогда ∠AH2H3 = ∠AHH3 = ∠ABC, значит, сторона H2H3 антипараллельна стороне BC. Аналогично доказывается антипараллельность двух других сторон треугольника
Свойство 2. Высоты треугольника ABC являются биссектрисами внутренних углов треугольника H1H2H3.
Свойство 3. Отрезок OA перпендикулярен отрезку H2H3.
Доказательство. Действительно, если описать окружность около треугольника H1H2H3, дуги, на которые опираются углы ∠H2H1A и ∠AH1H3, равны, а значит, OA⊥H2H3 (рис. 2).
Свойство 4. Вершины треугольника ABC являются центрами вневписанных окружностей ортоцентрического треугольника H1H2H3 (рис. 3).
Доказательство. Поскольку отрезок AH2 перпендикулярен биссектрисе H2B, а AH3⊥CH3, то пересечение отрезков AH2 и AH3, – точка A есть центр вневписанной окружности, касающейся стороны H2H3.
Свойство 5. Имеет место формула pH = hasinA, где pH — полупериметр треугольника H1H2H3, ha — высота AH1.
Доказательство. Из точки A опустим перпендикуляр AF на прямую H1H3 (рис.3). Поскольку∠H1AF = ∠H3H1B (углы с взаимно перпендикулярными сторонами), то ∠HAF = ∠A и H1F = hasinA (из треугольника H A1 F), или pH = hasinA.
Свойство 6. Имеет место формула S = RpH, где S — площадь треугольника ABC, R — радиус окружности, описанной около треугольника ABC.
Доказательство. Действительно, поскольку pH = hasinA, то
pH= sinA, и S = RpH(a — длина стороны BC).
Свойство 7. Окружность Леонарда Эйлера.
Доказательство. Опишем окружность около треугольника H1H2H3. Докажем, что окружности (обозначим её γe), кроме точек H1, H2, H3, принадлежат середины отрезков AH, BH, CH (их называют точками Эйлера и обозначают E1, E2, E3), ещё три точки M1, M2, M3 — середины сторон BC, AC, AB. Начнём с точек Эйлера. Заметим, что доказательство нестандартно (рис. 4).
Поскольку прямая H H1 (рис. 4) принадлежит биссектрисе угла ∠H2H1H3, то точка её пересечения с окружностью γe, описанной
около треугольника H1H2H3, будет серединой дуги H2H3, то есть точкой W1 треугольника H1H2H3, а точка A — центром вневписанной
окружности (свойство 4).
По теореме Мансиона ( IW1 = W1Ia = W1B = W1C): AE1 = E1H. Значит, точка совпадает с серединой отрезка IW1 для треугольника H1H2H3 с точкой E1. Поскольку точки B и C также центры вневписанных окружностей, то утверждение относительно середин отрезков AH, BH и CH доказано. Докажем, что середины AC, BC и AB (точки M1, M2, M3) принадлежат окружности γe.
Воспользуемся свойством вневписанных окружностей с центрами Ib и Ic. Пусть W1 A — точка, диаметрально противоположная точке W1. Тогда W1 A — середина отрезка IbIc. Пусть окружность γe пересекает сторону BC в точке X (рис. 4). Поскольку ∠E1H1X1 = 90°, то точки X и E1 диаметрально противоположны, а поскольку точка E1 есть точкой W1 окружности, то точка X совпадает с серединой отрезка BC (точки B и C — центры вневписанных окружностей). Теорема об окружности Эйлера для треугольника ABC доказана новым способом.
ІІ. Ортоудвоенный треугольник
Высоты AH1, BH2, CH3 продолжим до пересечения с описанной окружностью (рис. 5).
Получим треугольник N1N2N3, который назовём ортоудвоенным. Поскольку HH1 = H1N1, HH2 = H2N2, HH3 = H3N3, то этот треугольник гомотетичен треугольнику H1H2H3 с центром гомотетии — серединой отрезка OE ( E — центр окружности Эйлера) и коэффициентом гомотетии k =
Свойство 1. Вершины треугольника ABC делят дуги N2N3, N3N1, N1N2 пополам.
Доказательство. Действительно, ∠ N2N1A = ∠ N3N1A.
Свойство 2. Высоты треугольника ABC принадлежат биссектрисам внутренних углов треугольника N1N2N3.
Доказательство. Действительно, это следует из свойства 1.
Свойство 3. Радиус OA перпендикулярен отрезкам N2N3 и H2H3.
Доказательство. Действительно, это следует из свойства 1.
Свойство 4. Точка, симметричная ортоцентру H относительно середины M1 отрезка BC принадлежит окружности, описанной около треугольника
Доказательство. Проведём диаметр AA1 (рис.6) и найдём точку X, гомотетичную точке A1. Поскольку A1X = XH, то отрезок OX — средняя линия треугольника
AA1H. Значит, он параллелен AH и равен
AH, то есть OX = OM1 и точка X совпадает с точкой M1 — серединой отрезка BC.
Свойство 5. Прямая Эйлера. Центроид M треугольника ABC принадлежит отрезку OH.
Доказательство. Проведём отрезок AM1 (рис. 6). Он пересечёт OH в точке Y. Поскольку то M1M : AM = 1 : 2, а значит, точка Y совпадает с точкой M1.
Окружность девяти точек
Около треугольника H1H2H3 опишем окружность γe. Её центр делит пополам отрезок OH (точка E). Середины отрезков AH, BH, CH (точки E1, E2, E3) гомотетичны точкам A, B и C и принадлежат окружности γe.
Докажем, что точки M1, M2, M3 принадлежат окружности γe.
Доказательство. Действительно, точки A1 и H симметричны относительно точки B. Кроме того, точки A1 и M1 гомотетичны, а значит, точка M1 принадлежит окружности γe.
ІІІ. Ортоцентрический треугольник Q1Q2Q3
Опишем окружность около треугольника ABC и построим точки W1,W2, W3 (середины дуг BC, AC, AB) (рис. 7).
Точку пересечения хорд W2W3 и AW1 обозначим Q1. Аналогично получим точки Q1 и Q3. По теореме «листа трилистника» имеем: IW1 = W1C. Поскольку ∪ AW2 = ∪ W2C, то
а значит, треугольник Q1Q2Q3 — ортоцентрический треугольник треугольника W1W2W3. В равнобедренном треугольнике IW1C IQ3 = Q3C. Аналогично, IQ1 = Q1A, следовательно, стороны треугольника Q1Q2Q3 вдвое меньше соответственных сторон треугольника ABC. Поэтому (применяем формулу S = RpH ) площадь треугольника W1W2W3 . (1°)
Поскольку окружность, описанная около треугольника Q1Q2Q3, есть окружность Эйлера треугольника W1W2W3, то девять точек принадлежат одной окружности: середины отрезков W1W3, W2W3, W1W2, IW1, IW2, IW3, IA, IB, IC.
ІV. Ортоцентрический треугольник ABC Рассмотрим треугольник, вершины которого — центры вневписанных окружностей Ia, Ib, Ic (рис.8).
Ортоцентрическим треугольником этого
треугольника будет треугольник ABC, так как
каждая из его вершин есть пересечение внутренней и внешней биссектрис. Поскольку радиус окружности, описанной около треугольника ABC будет R, то радиус окружности, описанной около треугольника IaIbIc будет 2R, а площадь SIaIbIc=2R⋅p.
Поскольку окружность, описанная около треугольника ABC, является окружностью Эйлера треугольника IaIbIc, то девять точек принадлежат одной окружности: вершины треугольника ABC, точки W1, W2, W3, середины
V. Треугольник, подобный ортоцентрическому треугольнику H1H2H3
Через вершины A, B и C проведём касательные к окружности, описанной около треугольника ABC. Получим треугольник T1T2T3 (рис. 9).
тангенциальным) вычисляют по формуле:
ST=R⋅pT, где R — радиус окружности, вписанной в треугольник T1T2T3.
Глава 2. Применение.
§ 1 Применение свойств ортотреугольника для решения задач
Задача 1.
Пусть и – высоты треугольника АВС. Докажите, что треугольник подобен треугольнику АВС. Чему равен коэффициент подобия?
подобен треугольнику АВС по теореме 1. Коэффициент подобия . В прямоугольных треугольниках и , . Значит, .
Следствием данной задачи будет следующее утверждение: каждая сторона ортотреугольника равна произведению противолежащей стороны на косинус противолежащего угла исходного треугольника.
Задача 2.
Треугольник АВС остроугольный, и угол ВАС равен α. На стороне ВС как на диаметре построена полуокружность, пересекающая стороны АВ и АС в точках Р и Q соответственно. Найдите отношение площадей треугольников АВС и APQ.
Поскольку и – высоты треугольника , треугольник подобен с коэффициентом подобия , поэтому
Задача 3
В остроугольном треугольнике АВС проведены высоты АD, ВЕ и СF. Докажите, что pR=Pr, где p-периметр треугольника EDF, Р – периметр треугольника АВС.
Решение(без применения свойств):
1. Т.к. и согласно задаче 1 , то . ,
Пусть О – центр описанной окружности , R – ее радиус. Тогда Т.к. по т. синусов , то после подстановки, получаем .
Аналогично и , т.е. . Поскольку и , то , что и требовалось доказать.
Решение(без применения свойств):
По свойству 6 . , тогда , что и требовалось доказать.
Задача 4
Треугольник АВС остроугольный, и . Определите углы высотного треугольника.
1. Строим высоты , , .
Задача 5.
Т.к. – равнобедренный, то – высота, медиана, биссектриса ;.
4. Т.к. подобен , то; .
5. ||, а это значит, что подобен .
7. По т. Пифагора .
Задача 6
В равнобедренном треугольнике ABC(AB = BC)проведены высоты AA1,
Т.к. подобен , то и (1)
по гипотенузе и острому углу, т.к рассматриваемые треугольники прямоугольные, .
Т.к. и , отсекая пропорциональные отрезки, то ||.
Известно, что , , поэтому, подставив данные в (1), получим ,
Глава 3. Анкетирование учащихся
Всем ученикам 10 и 11 классов я задала по 4 вопроса:
Знаете ли вы об ортоцентрических треугольниках?
Применяли ли вы свойства ортоцентрических треугольников при решении задач?
Как вы считаете, можно ли облегчить решение задач, используя эти свойства?
Хотели бы вы научиться решать задачи на применение свойств ортоцентрических треугольников?
Подсчитав ответы «да», я получила следующие результаты:
Периметр равнобедренного треугольника

Средняя оценка: 4.5
Всего получено оценок: 122.
Средняя оценка: 4.5
Всего получено оценок: 122.
Периметр – это сумма длин всех сторон фигуры. Эта характеристика, наравне с площадью, одинаково востребована для всех фигур. Формула периметра равнобедренного треугольника логично вытекает из его свойств, но формула не столь сложна, как получение и закрепление практических навыков.
Формула вычисления периметра
Боковые стороны равнобедренного треугольника равны между собой. Это вытекает из определения и хорошо видно даже из названия фигуры. Именно из этого свойства и вытекает формула периметра:
P=2a+b, где b – это основание треугольника, a – значение боковой стороны.
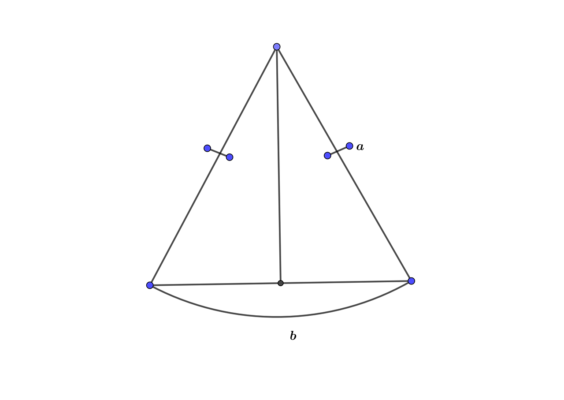
Из формулы видно, что для нахождения периметра достаточно знать величину основания и одной из боковых сторон. Рассмотрим несколько задач на нахождение периметра равнобедренного треугольника. Задачи будем решать по мере возрастания сложности, это позволит лучше понять способ размышления, которому нужно следовать для нахождения периметра.
Задача 1
- В равнобедренном треугольнике основание равно 6, а высота, проведенная к этому основанию, равна 4. Необходимо найти периметр фигуры.
Высота равнобедренного треугольника, проведенная к основанию, является также медианой и биссектрисой. Это свойство очень часто используется при решении задач, связанных с равнобедренными треугольниками.
Треугольник АВС высотой ВM делится на два прямоугольных треугольника: АВM и ВСM. В треугольнике АВM катет ВM известен, катет АM равен половине основания треугольника АВС, так как ВM является медианой, биссектрисой и высотой. По теореме Пифагора найдем значение гипотенузы АВ.
Найдем периметр: P=AC+AB*2=6+5*2=16
Задача 2
- В равнобедренном треугольнике высота, проведенная к основанию, равна 10, а острый угол при основании 30 градусам. нужно найти периметр треугольника.
Эта задача осложнена отсутствием сведений о сторонах треугольника, но, зная значение высоты и угла, в прямоугольном треугольнике ABH можно найти катет AH, а после решение пойдет по тому же сценарию, что и в задаче 1.
Найдем AH через значение синуса:
$$sin (ABH)==<1over2>$$ – синус 30 градусов является табличным значением.
Выразим нужную сторону:
Через котангенс найдем значение AH:
$$AH=>=10*sqrt<3>=17,32$$ – получившееся значение округлим до сотых.
Теперь, когда все требуемые значения найдены, определим периметр:
Задача 3
- В равнобедренном треугольнике ABC известна площадь, которая равна $$16oversqrt<3>$$ и острый угол при основании 30 градусов. Найти периметр треугольника.
Значения в условии часто приводятся в виде произведения корня на число. Это делается, чтобы максимально оградить последующее решение от погрешностей. Округлять результат лучше в конце вычислений
При такой постановке задачи может показаться, что решений нет, ведь сложно выразить одну из сторон или высоту из имеющихся данных. Попробуем решить по-другому.
Обозначим высоту и половину основания латинскими буквами: BH=h и AH=a
Тогда основание будет равно: AC=AH+HC=AH*2=2a
С другой стороны, значение h можно выразить из треугольника ABH через тангенс острого угла. Почему именно тангенс? Потому что в треугольнике ABH мы уже обозначили два катета a и h. Нужно выразить одно через другое. Два катета вместе связывают тангенс и котангенс. Традиционно к котангенсу и косинусу обращаются, только если не подходит тангенс или синус. Это не правило, можно решать так, как удобно, просто так принято.
Подставим полученное значение в формулу площади.
Подставим значение a в формулу площади и определим значение высоты:
Через теорему Пифагора найдем боковую сторону треугольника:
Подставим значения в формулу периметра:
Что мы узнали?
Мы разобрались подробно во всех тонкостях нахождения периметра равнобедренного треугольника. Решили три задачи разного уровня сложности, показав на примере, как решаются типовые задачи на решение равнобедренного треугольника.
[spoiler title=”источники:”]
http://school-science.ru/3/7/32641
http://obrazovaka.ru/matematika/perimetr-ravnobedrennogo-treugolnika-formula.html
[/spoiler]
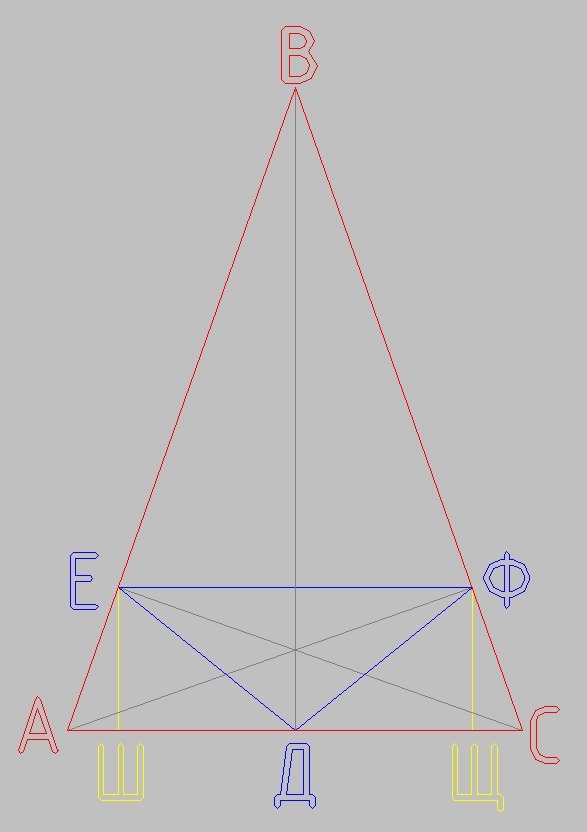
Ортотреугольник – это треугольник, вписанный в исходный, вершинами которого являются основания высот исходного.
— 1 —
Площадь исходного треугольника через основание и высоту к нему
S = 1/2*АС*ВД = 1/2*2*ВД = ВД
ВД по т. Пифагора из ΔАВД
ВД² = АВ² – АД² = 3² – 1² = 9 – 1 = 8
ВД = √8 = 2√2
S = 2√2
— 2 —
Площадь через высоту к боковой стороне
S = 1/2*АВ*ЕС = 1/2*3*ЕС = 2√2
ЕС = 4√2/3
— 3 —
в прямоугольном ΔАЕС
Д – середина гипотенузы, значит
АД = ДС = ЕД = 1 (радиус описанной окружности)
— 4 —
в ΔАЕС катет АЕ по т. Пифагора
АЕ² = АС² – ЕС² = 2² – (4√2/3)² = 4 – 16*2/9 = 4 – 32/9 = 36/9 – 32/9 = 4/9
АЕ = 2/3
— 5 —
ΔАЕШ ~ ΔАЕС, поскольку угол А общий, второй угол прямой, из подобия
АШ/АЕ = АЕ/АС
АШ = АЕ²/АС = 4/9/2 = 2/9
— 6 —
ЕФ = АС – АШ – ЩС = АС – 2*АШ = 2 – 2*2/9 = 2 – 4/9 = 18/9 – 4/9 = 14/9
— 7 —
Периметр отртотреугольника
P = ЕД + ДФ + ЕФ = 1 + 1 + 14/9 = 18/9 + 14/9 = 32/9