Правильная четырехугольная призма
Определение.
Правильная четырехугольная призма – это шестигранник, основаниями которого являются два равных квадрата, а боковые грани представляют собой равные прямоугольники
Боковое ребро – это общая сторона двух смежных боковых граней
Высота призмы – это отрезок, перпендикулярный основаниям призмы
Диагональ призмы – отрезок, соединяющий две вершины оснований, которые не принадлежат к одной грани
Диагональная плоскость – плоскость, которая проходит через диагональ призмы и ее боковые ребра
Диагональное сечение – границы пересечения призмы и диагональной плоскости. Диагональное сечение правильной четырехугольной призмы представляет собой прямоугольник
Перпендикулярное сечение (ортогональное сечение) – это пересечение призмы и плоскости, проведенной перпендикулярно ее боковым ребрам
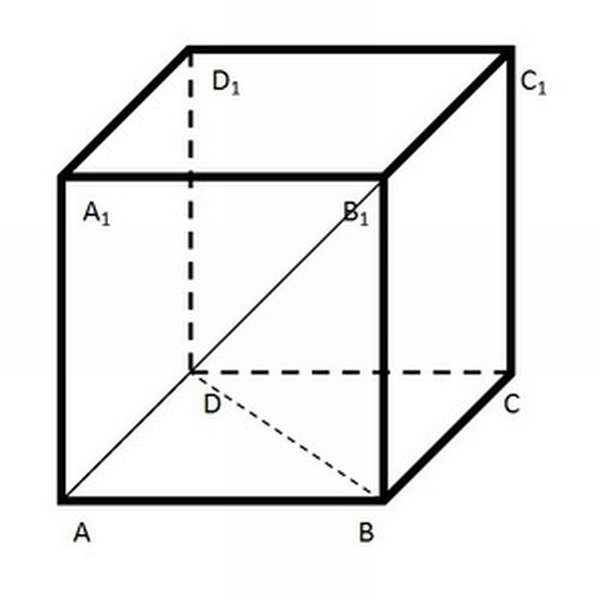
Элементы правильной четырехугольной призмы
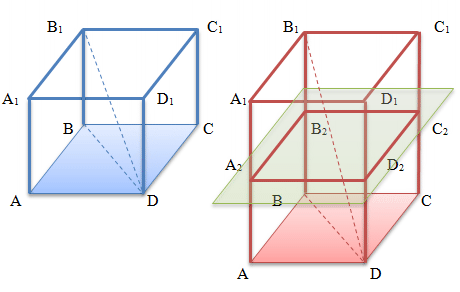
На рисунке изображены две правильные четырехугольные призмы, у которых обозначены соответствующими буквами:
- Основания ABCD и A1B1C1D1 равны и параллельны друг другу
- Боковые грани AA1D1D, AA1B1B, BB1C1C и CC1D1D, каждая из которых является прямоугольником
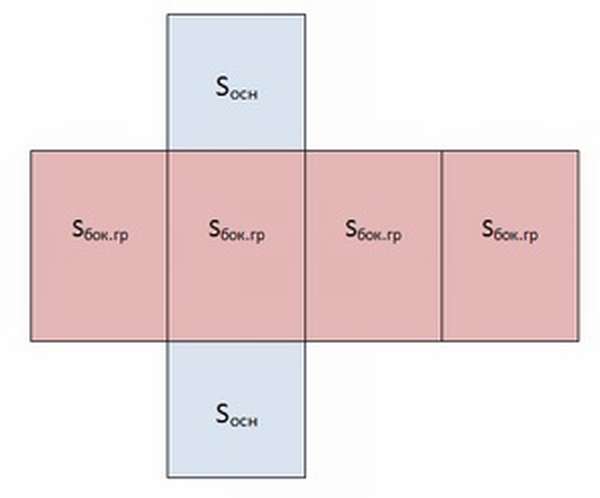
- Боковая поверхность – сумма площадей всех боковых граней призмы
- Полная поверхность – сумма площадей всех оснований и боковых граней (сумма площади боковой поверхности и оснований)
- Боковые ребра AA1, BB1, CC1 и DD1.
- Диагональ B1D
- Диагональ основания BD
- Диагональное сечение BB1D1D
- Перпендикулярное сечение A2B2C2D2 .
Свойства правильной четырехугольной призмы
- Основаниями являются два равных квадрата
- Основания параллельны друг другу
- Боковыми гранями являются прямоугольники
- Боковые грани равны между собой
- Боковые грани перпендикулярны основаниям
- Боковые ребра параллельны между собой и равны
- Перпендикулярное сечение перпендикулярно всем боковым ребрам и параллельно основаниям
- Углы перпендикулярного сечения – прямые
- Диагональное сечение правильной четырехугольной призмы представляет собой прямоугольник
- Перпендикулярное (ортогональное сечение) параллельно основаниям
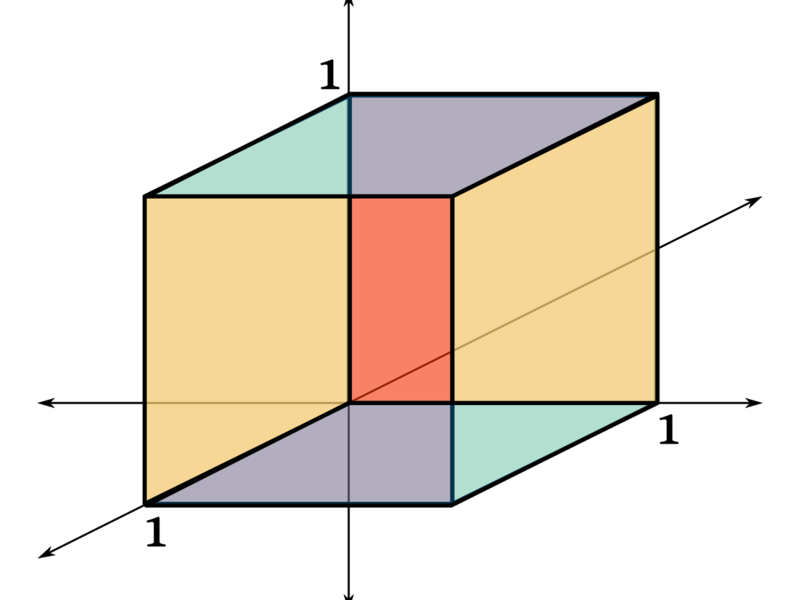
Формулы для правильной четырехугольной призмы
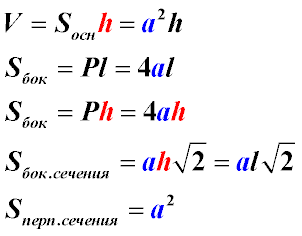
Указания к решению задач
При решении задач на тему “правильная четырехугольная призма” подразумевается, что:
Правильная призма — призма в основании которой лежит правильный многоугольник, а боковые ребра перпендикулярны плоскостям основания. То есть правильная четырехугольная призма содержит в своем основании квадрат. (см. выше свойства правильной четырехугольной призмы)
Примечание. Это часть урока с задачами по геометрии (раздел стереометрия – призма). Здесь размещены задачи, которые вызывают трудности при решении. Если Вам необходимо решить задачу по геометрии, которой здесь нет – пишите об этом в форуме. Для обозначения действия извлечения квадратного корня в решениях задач используется символ √ .
Задача.
В правильной четырёхугольной призме площадь основания 144 см2, а высота 14 см. Найти диагональ призмы и площадь полной поверхности.
Решение.
Правильный четырехугольник – это квадрат.
Соответственно, сторона основания будет равна
√144 = 12 см.
Откуда диагональ основания правильной прямоугольной призмы будет равна
√( 122 + 122 ) = √288 = 12√2
Диагональ правильной призмы образует с диагональю основания и высотой призмы прямоугольный треугольник. Соответственно, по теореме Пифагора диагональ заданной правильной четырехугольной призмы будет равна:
√( ( 12√2 )2 + 142 ) = 22 см
Ответ: 22 см
Задача
Определите полную поверхность правильной четырехугольной призмы, если ее диагональ равна 5 см, а диагональ боковой грани равна 4 см.
Решение.
Поскольку в основании правильной четырехугольной призмы лежит квадрат, то сторону основания (обозначим как a) найдем по теореме Пифагора:
a2 + a2 = 52
2a2 = 25
a = √12,5
Высота боковой грани (обозначим как h) тогда будет равна:
h2 + 12,5 = 42
h2 + 12,5 = 16
h2 = 3,5
h = √3,5
Площадь полной поверхности будет равна сумме площади боковой поверхности и удвоенной площади основания
S = 2a2 + 4ah
S = 25 + 4√12,5 * √3,5
S = 25 + 4√43,75
S = 25 + 4√(175/4)
S = 25 + 4√(7*25/4)
S = 25 + 10√7 ≈ 51,46 см2 .
Ответ: 25 + 10√7 ≈ 51,46 см2 .
15306.1214
Прямая призма |
Описание курса
| Куб
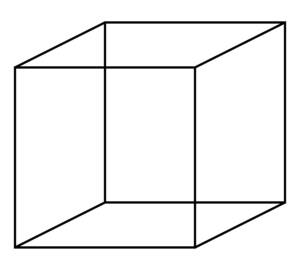
Как выглядит призма
Правильной четырёхугольной призмой называется шестигранник, в основаниях которого находятся 2 квадрата, а боковые грани представлены прямоугольниками. Иное название для этой геометрической фигуры — прямой параллелепипед.
Рисунок, на котором изображена четырёхугольная призма, показан ниже.
На картинке также можно увидеть важнейшие элементы, из которых состоит геометрическое тело. К ним принято относить:
Основы призмы — квадраты LMNO и L₁M₁N₁O₁.
- Боковые грани — прямоугольники MM₁L₁L, LL₁O₁O, NN₁O₁O и MM₁N₁N, расположенные под прямым углом к основаниям.
- Боковые рёбра — отрезки, расположенные на стыке между двумя боковыми гранями: M₁M, N₁N, O₁O и L₁L. Также выполняют роль высоты (поскольку лежат в параллельной основаниям плоскости). В призме боковые рёбра всегда равны между собой — это одно из важнейших свойств этого геометрического тела.
- Диагонали, которые, в свою очередь, подразделяются ещё на 3 категории. К ним относится 4 диагонали основания (MO, N₁L₁), 8 диагоналей боковых граней (ML₁, O₁L) и 4 диагонали призмы, начала и концы которых являются вершинами 2 разных оснований и боковых сторон (MO₁, N₁L).
Иногда в задачах по геометрии можно встретить понятие сечения. Определение будет звучать так: сечение — это все точки объёмного тела, принадлежащие секущей плоскости. Сечение бывает перпендикулярным (пересекает рёбра фигуры под углом 90 градусов). Для прямоугольной призмы также рассматривается диагональное сечение (максимальное количество сечений, которых можно построить — 2), проходящее через 2 ребра и диагонали основания.
Если же сечение нарисовано так, что секущая плоскость не параллельна ни основам, ни боковым граням, в результате получается усечённая призма.
Для нахождения приведённых призматических элементов используются различные отношения и формулы. Часть из них известна из курса планиметрии (например, для нахождения площади основания призмы достаточно вспомнить формулу площади квадрата).
Площадь поверхности и объём
Чтобы определить объём призмы по формуле, необходимо знать площадь её основания и высоту:
V = Sосн·h
Так как основанием правильной четырёхгранной призмы является квадрат со стороной a, можно записать формулу в более подробном виде:
V = a²·h
Если речь идёт о кубе — правильной призме с равной длиной, шириной и высотой, объём вычисляется так:
V = a³
Чтобы понять, как найти площадь боковой поверхности призмы, необходимо представить себе её развёртку.
Из чертежа видно, что боковая поверхность составлена из 4 равных прямоугольников. Её площадь вычисляется как произведение периметра основания на высоту фигуры:
Sбок = Pосн·h
С учётом того, что периметр квадрата равен P = 4a, формула принимает вид:
Sбок = 4a·h
Для куба:
Sбок = 4a²
Для вычисления площади полной поверхности призмы нужно к боковой площади прибавить 2 площади оснований:
Sполн = Sбок + 2Sосн
Применительно к четырёхугольной правильной призме формула имеет вид:
Sполн = 4a·h + 2a²
Для площади поверхности куба:
Sполн = 6a²
Зная объём или площадь поверхности, можно вычислить отдельные элементы геометрического тела.
Нахождение элементов призмы
Часто встречаются задачи, в которых дан объём или известна величина боковой площади поверхности, где необходимо определить длину стороны основания или высоту. В таких случаях формулы можно вывести:
- длина стороны основания: a = Sбок / 4h = √(V / h),
- длина высоты или бокового ребра: h = Sбок / 4a = V / a²,
- площадь основания: Sосн = V / h,
- площадь боковой грани: Sбок. гр = Sбок / 4.
Sдиаг = ah√2
Для вычисления диагонали призмы используется формула:
dприз = √(2a² + h²)
Чтобы понять, как применять приведённые соотношения, можно попрактиковаться и решить несколько несложных заданий.
Примеры задач с решениями
Вот несколько заданий, встречающихся в государственных итоговых экзаменах по математике.
Задание 1.
В коробку, имеющую форму правильной четырёхугольной призмы, насыпан песок. Высота его уровня составляет 10 см. Каким станет уровень песка, если переместить его в ёмкость такой же формы, но с длиной основания в 2 раза больше?
Решение.
Следует рассуждать следующим образом. Количество песка в первой и второй ёмкости не изменялось, т. е. его объём в них совпадает. Можно обозначить длину основания за a. В таком случае для первой коробки объём вещества составит:
V₁ = ha² = 10a²
Для второй коробки длина основания составляет 2a, но неизвестна высота уровня песка:
V₂ = h (2a)² = 4ha²
Поскольку V₁ = V₂, можно приравнять выражения:
10a² = 4ha²
После сокращения обеих частей уравнения на a² получается:
10 = 4h
В результате новый уровень песка составит h = 10 / 4 = 2,5 см.
Задание 2.
ABCDA₁B₁C₁D₁ правильная призма. Известно, что BD = AB₁ = 6√2. Найти площадь полной поверхности тела.
Решение.
Чтобы было проще понять, какие именно элементы известны, можно изобразить фигуру.
Поскольку речь идёт о правильной призме, можно сделать вывод, что в основании находится квадрат с диагональю 6√2. Диагональ боковой грани имеет такую же величину, следовательно, боковая грань тоже имеет форму квадрата, равного основанию. Получается, что все три измерения — длина, ширина и высота — равны. Можно сделать вывод, что ABCDA₁B₁C₁D₁ является кубом.
Длина любого ребра определяется через известную диагональ:
a = d / √2 = 6√2 / √2 = 6
Площадь полной поверхности находится по формуле для куба:
Sполн = 6a² = 6·6² = 216
Задание 3.
В комнате производится ремонт. Известно, что её пол имеет форму квадрата с площадью 9 м². Высота помещения составляет 2,5 м. Какова наименьшая стоимость оклейки комнаты обоями, если 1 м² стоит 50 рублей?
Решение.
Поскольку пол и потолок являются квадратами, т. е. правильными четырёхугольниками, и стены её перпендикулярны горизонтальным поверхностям, можно сделать вывод, что она является правильной призмой. Необходимо определить площадь её боковой поверхности.
Длина комнаты составляет a = √9 = 3 м.
Обоями будет оклеена площадь Sбок = 4·3·2,5 = 30 м².
Наименьшая стоимость обоев для этой комнаты составит 50·30 = 1500 рублей.
Таким образом, для решения задач на прямоугольную призму достаточно уметь вычислять площадь и периметр квадрата и прямоугольника, а также владеть формулами для нахождения объёма и площади поверхности.
Как найти площадь куба
Проститутки Ростов на Дону rostovchanotki.ru
Подскажите формулу периметра основания прямой призмы
Gosudar
Мастер
(1084),
на голосовании
7 лет назад
Голосование за лучший ответ
Grigno76
Мыслитель
(6479)
7 лет назад
Периметр это сумма длин сторон основания призмы. Т. е. тебе нужен периметр многоугольников:)
Похожие вопросы
You can see prisms in both math class and throughout your everyday life. A brick is a rectangular prism. A carton of orange juice is a type of prism. A tissue box is a rectangular prism. Barns are a type of pentagonal prism. The pentagon is a pentagonal prism. A fish tank is a rectangular prism. This list goes on and on.
Prisms by definition are solid objects with identical end shapes, identical cross sections and flat side faces (no curves). And while most math problems and real world examples regarding prism calculations have to do with a volume formula or a surface area formula, there’s one calculation that you need to understand first before you can do that: the perimeter of a prism.
What Is a Prism?
The general definition of a prism is a 3-dimensional solid shape that has the following characteristics:
- It is a polyhedron (meaning it is a solid figure).
- The cross section of the object is the exact same throughout the length of the object.
- It is a parallelogram (a 4-sided shape where the opposite sides are parallel to each other).
- The faces of the object are flat (no curved faces).
- The two end shapes are identical.
The name of the prism comes from the shape of the two ends, which are known as the bases. This can be any shape (besides curves or circles). For example, a prism with triangular bases is called a triangular prism. A prism with rectangular bases is called a rectangular prism. This list goes on.
Looking at the characteristics of prisms, this eliminates spheres, cylinders and cones as prisms because they have curved faces. This also eliminates pyramids because they don’t have identical base shapes or identical cross sections throughout.
Perimeter of Prism
When talking about the perimeter of the prism, you’re actually referring to the perimeter of the base shape. The perimeter of the base of a prism is the same as the perimeter along any cross section of the prism since all cross sections are the same along the length of the prism.
Perimeter measures the sum of the lengths of any polygon. So for each prism type, you’d find the sum of the lengths of whatever shape is the base, and that would be the perimeter of the prism.
The formula for finding the perimeter of a triangular prism, for example, would be the sum of the three lengths of the triangle that makes up the base, or:
text{Perimeter of triangle } = a + b + c
where a, b and c are the three lengths of the triangle.
This would be the perimeter of a rectangular prism formula:
text{ Perimeter of rectangle } = 2l + 2w
where l is the length of the rectangle and w is the width.
Apply standard perimeter calculations to the base shape of the prism, and that gives you the perimeter.
Why Would You Need to Calculate the Perimeter of a Prism?
Finding the perimeter of a prism doesn’t seem too complex once you understand what’s being asked. However, the perimeter is an important calculation that factors into surface area and volume formulas for some prisms.
For example, this is the formula for finding the surface area of a right prism (a right prism has identical bases and sides that are all rectangular):
text{Surface Area } = 2b + ph
where b is equal to area of the base, p is equal to the perimeter of the base and h is equal to the height of the prism. You can see that perimeter essential for finding the surface area.
Example Problem: Perimeter of a Rectangular Prism
Let’s say you’re given a problem with a right rectangular prism and you’re asked to find the perimeter. You’re given the following values:
Length = 75 cm
Width = 10 cm
Height = 5 cm
To find the perimeter, use the formula for finding the perimeter of a rectangular prism since the name tells you the base is a rectangle:
begin{aligned} text{Perimeter } &= 2l + 2w \ &= 2(75 text{ cm}) + 2(10 text{ cm} ) \ &= 150 text{ cm} + 20 text{ cm} \ &= 170 text{ cm} end{aligned}
You can then go on to find the surface area because you’re given the height, you have the perimeter of the base and it’s given that this prism is a right prism.
The area of the base is equal to length × width (as it always is for a rectangle), which is:
begin{aligned} text{ Area of base } &= 75 text{ cm} × 10 text{ cm} \ &= 750 text{ cm}^2 end{aligned}
Now you have all the values for a surface area calculation:
begin{aligned} text{ Surface Area } &= 2b + ph \ &= 2(750 text{ cm}^2) + 170 text{ cm}(5 text{ cm}) \ &= 1500 text{ cm}^2 + 850 text{ cm}^2 \ &= 2350 text{ cm}^2 end{aligned}
Как найти периметр призмы
Любая геометрическая фигура имеет несколько измерений. Одно из них – периметр. Найти его, как правило, проще всего. Нужно лишь знать размер всех сторон геометрической фигуры.
Вам понадобится
- Линейка, лист бумаги, ручка.
Инструкция
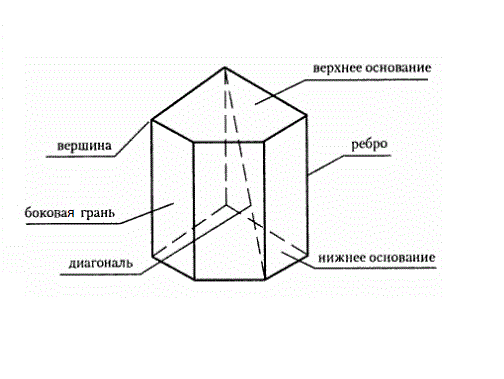
Разберитесь, что такое призма, и какой вид эта геометрическая фигура может иметь. Учтите, что слово «призма» переводится с латинского как «нечто отпиленное». Этот многогранник, всегда имеет два основания, которые расположены в параллельных плоскостях и являются равными многоугольниками. Они могут быть треугольными, четырехугольными, а также n-угольными.
Запомните, что количество остальных (боковых) граней зависит от вида основания. Если в основании треугольник, боковых граней соответственно окажется три, четырехугольник – четыре и так далее.
Имейте в виду, что ребра боковое ребро располагается под углом 90о к основанию, призма именуется прямой. В противном случае – наклонной. Если у прямой призмы в основании окажется правильный многоугольник, она превратится в правильную призму. Пример подобной геометрической фигуры – куб.
Чтобы вычислить периметр призмы, найдите периметры оснований и боковых граней призмы, и все размеры сложите друг с другом. Для этого измерьте при помощи линейки длины сторон (или ребра) каждой из граней. И посчитайте периметр каждого многоугольника.
Упростите свою задачу. Так как размер обоих оснований одинаков, померяйте длины ребер только у одного из них. Сложите размеры всех сторон и умножьте получившуюся сумму на два.
Если у оснований есть ребра равного размера, найдите количество одинаковых боковых граней. Измерьте длины сторон одной из этих граней, вычислите ее периметр. Умножьте получившееся значение на общее число одинаковых граней.
Отдельно посчитайте периметр каждой из тех боковых граней, которая ни разу не повторяется.
Сложите все посчитанные периметры – двух оснований, повторяющихся боковых граней, и тех боковых граней, которые не имеют аналога. Общая сумма будет равна периметру призмы.
Обратите внимание
Вычисление периметра не зависит от вида призмы. Он подсчитывается одинаково и для прямой, и для наклонной призмы.
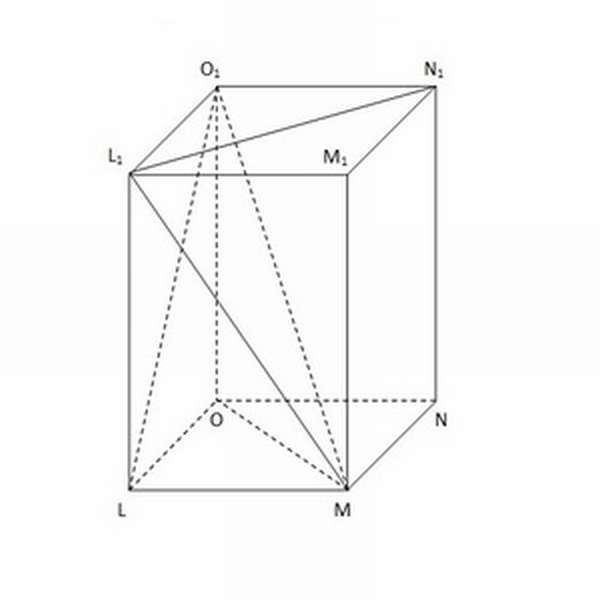 Основы призмы — квадраты LMNO и L₁M₁N₁O₁.
Основы призмы — квадраты LMNO и L₁M₁N₁O₁.