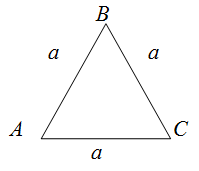
Как найти периметр основания равностороннего треугольника

Как найти периметр основания равностороннего треугольника

Чтобы найти периметр равностороннего треугольника(или найти периметр правильного треугольника), нужно знать его сторону.

В общем случае для нахождения периметра треугольника используют формулу

    [P = a + b + c]

perimetr ravnostoronnego treugolnika

Поскольку в равностороннем треугольнике все три стороны равны, формула упрощается:

    [P = a + a + a = 3 cdot a]

Таким образом, формула периметра равностороннего треугольника:

    [P = 3a]

(а — длина его стороны).

Примеры.

1) Найти периметр равностороннего треугольника, сторона которого равна 10 см.

Решение:

По формуле Р=3а имеем: Р=3∙10=30 (см).

2) Периметр равностороннего треугольника равен 21 см. Найти его сторону.

Решение:

Р=3а, значит, а=Р:3. Таким образом, длина стороны треугольника равна а=21:3= 7 (см).

perimetr pravilnogo treugolnika 3) Найти периметр правильного треугольника АВС, если АВ=25 см.

Решение:

По формуле P=3a, P=3∙АВ=3∙25=75 (см).

Источник

Содержание:

  • Формула
  • Примеры вычисления периметра равностороннего треугольника

Формула

Чтобы найти периметр равностороннего треугольника, надо длину его стороны умножить на три.

Периметр равностороннего треугольника – это сумма длин его сторон. У равностороннего треугольника
все стороны равны. Поэтому чтобы найти периметр равностороннего треугольника
$ABC$, со стороной
$a$ нужно воспользоваться формулой

$$P_{Delta A B C}=a+a+a=3 a$$

Примеры вычисления периметра равностороннего треугольника

Пример

Задание. Найти периметр треугольника
$ABC$ со стороной, равной 5 дм.

Решение. Воспользуемся формулой для нахождения периметра равностороннего треугольника:

$$P_{Delta A B C}=3a$$

Тогда искомый периметр равен:

$P_{Delta A B C}=3 cdot 5=15$ (дм)

Ответ. $P_{Delta A B C}=15$ (дм)

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Периметр равностороннего треугольника
$ABC$ равен
27 см. Найти длины его стороны.

Решение. Периметр равностороннего треугольника вычисляется по формуле:

$$P_{Delta A B C}=3 a$$

Подставим в нее заданное значение периметра и выразим из полученного уравнения искомую длину
$a$:

$27=3 a Rightarrow a=27: 3=9$ (см)

Ответ. $a=9$ (см)

Читать дальше: как найти периметр круга.

Источник

Периметр равностороннего треугольника


Периметр равностороннего треугольника

4.4

Средняя оценка: 4.4

Всего получено оценок: 325.

4.4

Средняя оценка: 4.4

Всего получено оценок: 325.

Равносторонний треугольник занимает особое место среди треугольников. Для того, чтобы найти значение периметра, площади, углов или радиусов окружностей вписанной и описанной у равнобедренного треугольника, достаточно знать величину стороны. С одной стороны, это значительно облегчает решение, с другой составители задач редко дают значение стороны и приходится искать обходные пути решения.

Формула нахождения периметра равностороннего треугольника

Формула периметра равностороннего треугольника вытекает из определений. Что такое периметр? Периметр это сумма всех сторон фигуры. Равносторонний треугольник – это треугольник, все стороны которого равны.

Рис. 1. Равносторонний треугольник

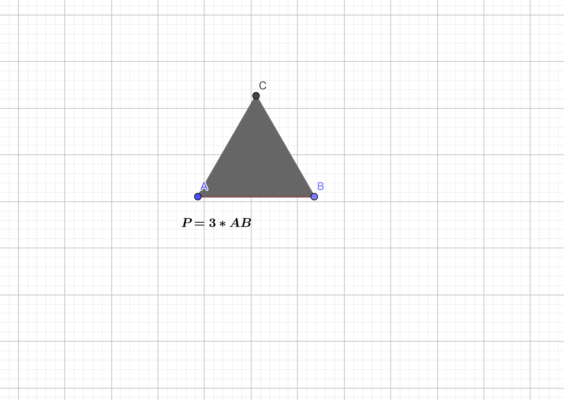
Значит,для того, чтобы найти значение периметра достаточно умножить величину стороны на количество сторон:

P=3*a

Решим несколько разных по сложности задач, чтобы разобраться, какие проблемы могут встречаться на пути нахождения периметра.

Задача 1

  • В равностороннем треугольнике сторона равна 6. Найти периметр треугольника.

Это самый простой вариант задачи. Достаточно подставить значение в формулу и получить результат. Такая задача не должна вызывать затруднений:

P=3*a=3*6=18

Задача 2

  • В равнобедренном треугольнике острый угол при основании равен 60 градусам, площадь треугольника равна $${64oversqrt{3}}$$.

Особое внимание нужно обращать на вид фигуры, который указан в условии задачи.

В данной задаче дан равнобедренный треугольник. Чтобы воспользоваться общей формулой, необходимо доказать, что этот равнобедренный треугольник является еще и равносторонним.

Обратим внимание на величину угла. Угол при основании равен 60. При этом углы у основания равнобедренного треугольника равны, а сумма углов любого треугольника равна 180 градусов. Значит у основания два угла по 60 градусов. Рассчитаем угол при вершине:

180-60-60=60 – угол при вершине так же равен 60 градусам.

Значит, данный треугольник будет равносторонним, так как все углы равны 60 градусам.

Углы по 60 градусов характерны только для равностороннего треугольника. Именно сочетание 3 равных сторон образует 3 равных угла. В любых других ситуациях, хотя бы один угол будет отличаться.

Для площади равностороннего треугольника имеется отдельная формула:

$$S=a^2*{sqrt{3}over 4}={64oversqrt{3}}$$ – где а значение стороны, которое нам и нужно выразить из этой формулы.

$$а^2={Sover{sqrt{3}over 4}}$$

$$a^2={4Soversqrt{3}}$$

$$a=sqrt{4Soversqrt{3}}$$

$$a={sqrt{4*{64oversqrt{3}^2}}oversqrt{3}}=sqrt{4*64}=16$$

Подставим полученное значение в формулу:

P=3*a=3*16=48

Задача 3

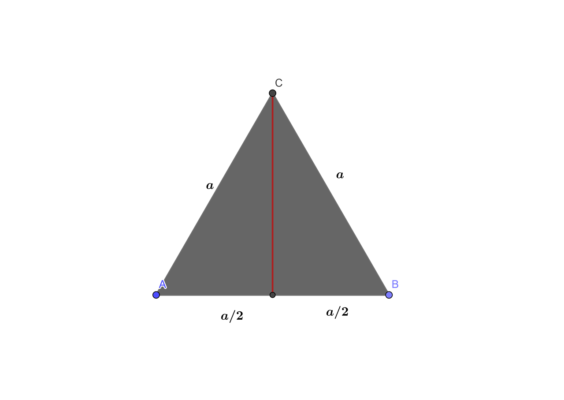
  • В равностороннем треугольнике высота равна $$3*sqrt{3}$$. Найти периметр треугольника.

Рис. 2. Рисунок к задаче 3

Для данной задачи нужно воспользоваться методом решения, который часто используется в задачах с равнобедренным треугольником. Из любой вершины опустим высоту, которая будет медианой и биссектрисой.

В одном из получившихся треугольников выразим значение высоты через сторону с помощью теоремы Пифагора:

$$h^2=a^2-({aover2})^2$$

$$h^2=a^2-{a^2over4}$$

Вычтем подобные слагаемые:

$$h^2={3over4}*a^2$$

Из получившейся формулы выразим значение стороны:

$$a^2={4over3}*h^2$$

$$a=sqrt{{4over3}*h^2}$$

$$a=sqrt{{4over3}*(3*sqrt{3})^2}$$

$$a=sqrt{{4over3}*(9*3)}$$

$$a=sqrt{4*9}$$

a=6

Рис. 3. Периметр равностороннего треугольника

Подставим получившееся значение в формулу периметра равностороннего треугольника.

P=3*a=3*6=18

Заключение

Что мы узнали?

Мы обсудили формулу для нахождения периметра равностороннего треугольника. Выделили проблемы, которые приходится решать при нахождении стороны равностороннего треугольника для дальнейшего решения задачи. Рассмотрели различные пути решения задач на нахождение периметра равностороннего треугольника.

Тест по теме

Доска почёта

Доска почёта

Чтобы попасть сюда – пройдите тест.

  • Марго Дудченко

    4/5

  • Татьяна Коробейникова

    5/5

  • Наташа Новак

    4/5

  • Марина Безобразова

    4/5

  • Даниил Толыпин

    5/5

  • Ибрагим Вафя-Сулим

    5/5

  • Наталия Левина

    4/5

  • Исмаил Тагиев

    5/5

Оценка статьи

4.4

Средняя оценка: 4.4

Всего получено оценок: 325.

А какая ваша оценка?

Источник

Периметр равностороннего треугольника

Чтобы найти периметр равностороннего треугольника(или найти периметр правильного треугольника), нужно знать его сторону.

В общем случае для нахождения периметра треугольника используют формулу

Поскольку в равностороннем треугольнике все три стороны равны, формула упрощается:

Таким образом, формула периметра равностороннего треугольника:

(а — длина его стороны).

1) Найти периметр равностороннего треугольника, сторона которого равна 10 см.

По формуле Р=3а имеем: Р=3∙10=30 (см).

2) Периметр равностороннего треугольника равен 21 см. Найти его сторону.

Р=3а, значит, а=Р:3. Таким образом, длина стороны треугольника равна а=21:3= 7 (см).

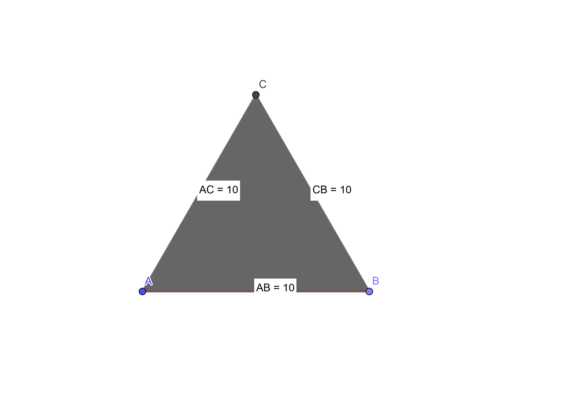
3) Найти периметр правильного треугольника АВС, если АВ=25 см.

Формула периметра равностороннего треугольника

Периметр равностороннего треугольника ABC , длины сторон которого соответственно равны AB = BC = CA = a равен тройной длинне стороны a

Периметр равностороннего треугольника вычисляется по формуле:

где a – стороны равностороннего треугольника.

Основные понятия, справедливые для треугольников

  • Сумма углов треугольника равна 180°.
  • Высота – это отрезок перпендикуляра, опущенного из вершины на противоположную сторону.
  • Центр описанной окружности лежит на пересечении медиатрис.
  • Медиатриса – это перпендикулярна прямая, проходящая через середину стороны.
  • Центр вписанной окружности лежит на пересечении биссектрис углов.
  • Биссектриса угла делит угол на две равные части.
  • Медиана – это отрезок, соединяющий вершину с серединой противоположной стороны.
  • Медианы пересекаются в центре тяжести, который делит каждую медиану в отношение 2:1.

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

О сайте

На нашем сайте вы найдете множество полезных калькуляторов, конвертеров, таблиц, а также справочных материалов по основным дисциплинам.

Самый простой способ сделать расчеты в сети — это использовать подходящие онлайн инструменты. Воспользуйтесь поиском, чтобы найти подходящий инструмент на нашем сайте.

calcsbox.com

На сайте используется технология LaTeX.
Поэтому для корректного отображения формул и выражений
пожалуйста дождитесь полной загрузки страницы.

© 2022 Все калькуляторы online

Копирование материалов запрещено

Периметр равностороннего треугольника — формула и примеры нахождения

В задачах по математике иногда приходится находить суммарное значение всех сторон равностороннего треугольника, формула периметра которого немного отличается от других фигур. Чтобы разбираться в материале, нужно ознакомиться с формулировками основных определений, а также доказать теорему практическим путем.

Общие сведения

Изучение любой фигуры, процесса или явления всегда начинается с определений. Треугольником называется геометрическое тело, состоящее из трех, не лежащих на одной прямой, вершин. Прямая — совокупность бесконечного количества точек, лежащих в одной плоскости и проходящих без искажений.

Вершина — точка, образованная сторонами треугольника. Периметр — суммарное значение всех сторон любой фигуры. Высота — отрезок, проведенный из любой вершины на сторону, которая является противоположной, под углом в 90 градусов.

Медиана — часть прямой, проведенной из вершины, но не под прямым углом, а соединяющая ее с серединой противолежащей стороны. Биссектриса — прямая, делящая угол на 2 равных величины.

Виды треугольников

Треугольники классифицируются по углам и сторонам. На основании первого критерия можно выделить несколько типов фигур:

  • Остроугольный.
  • Прямоугольный.
  • Тупоугольный.

    В первом случае у фигуры все углы острые, т. е. градусная мера каждого не должна превышать 90 градусов. Если хотя бы один из них эквивалентен 90, треугольник является прямоугольным. Однако когда градусная мера одного из них превышает 90, он принадлежит к третьему типу.

    Треугольники классифицируются еще и по сторонам. Распределение на группы происходит по такому принципу:

  • Величины всех сторон не равны между собой (произвольный или разносторонний).
  • Равны только значения двух боковых сторон (равнобедренный).
  • Все стороны эквивалентны одному числу (равносторонний или правильный).

    Равнобедренный треугольник можно считать прямоугольным и тупоугольным. Кроме того, равносторонняя фигура всегда является остроугольной. Далее необходимо перейти к доказательству теоремы о периметре.

    Теорема о периметре

    Каждому ученику известна формула периметра треугольника для 3 класса. Она является довольно примитивным соотношением, и применяется в абсолютно другом виде в старших классах и высших учебных заведениях. Математики предлагают рассмотреть доказательство теоремы о периметре правильного треугольника. Ее формулировка имеет следующий вид: периметр треугольника равен утроенному произведению одной из его сторон, когда фигура является правильной.

    Доказывается утверждение очень просто. Для этого необходимо использовать следующий алгоритм:

    Можно найти и другое доказательство теоремы, в которой используется прямоугольник. В фигуре нужно провести диагонали, а затем по формуле Пифагора выразить боковые стороны. Однако процесс доказательства утверждения является более сложным.

    У каждой теоремы есть какие-либо следствия. Они позволяют существенно оптимизировать вычисления при решении задач. Далее необходимо рассмотреть полезные формулы.

    Полезные формулы

    Для вычисления различных параметров треугольника применяются определенные формулы. Кроме того, вводится новая величина, которая называется полупериметром. Она обозначается литерой «р» и составляет половину от периметра, т. е. р=Р/2. Специалисты рекомендуют использовать следующие формулы (если известны исходные параметры):

  • Площадь (S) и высоту (l): Р=6S/l.
  • Cторона (t): Р=3t.
  • l: P=6l/(3)^(0.5).
  • Радиус описанного круга: Р=3R (3)^(½).
  • Величина радиуса вписанной окружности: Р=6r (3)^(½).
  • Через формулу Герона: Р=[(S 2 — (t-3)^2)]/[6t — 8].

    Последнее соотношение редко применяется при решении задач. Однако при известных величинах площади и одной из сторон правильного треугольника значения можно подставить сразу в формулу, а не тратить время на вычисление высоты.

    Пример решения задачи

    Для закрепления теоретического материала нужно решить задачу по геометрии. Ее условие имеет следующий вид:

  • Площадь равностороннего треугольника эквивалентна 12*(3)^(½) сантиметрам.
  • Если от значения площади S отнять сторону t (без учета единиц измерения), получится 8.
  • При делении S на t получается 3.

    В задаче нужно найти значение стороны. Чтобы выполнить эту операцию, необходимо составить 2 уравнения. Однако для начала требуется обозначить неизвестную величину переменной «t». В результате получается следующая система алгебраических выражений с неизвестными:

    Чтобы вычислить величину переменной, необходимо выразить ее в первом тождестве, т. е. t=S-8. После этого нужно подставить все известные значения: t=12*(3)^(½) — 8 = 4*(3)^(½). Для проверки правильности решения нужно воспользоваться вторым соотношением, которое позволит вычислять площадь: 4*(3)^(½) * 3 = 12*(3)^(½).

    Из последнего расчета можно сделать вывод, что сторона треугольника определена правильно и равна 4*(3)^(½). Значение периметра в этом случае будет равно 12*(3)^(½) сантиметров.

    Таким образом, для решения задач по геометрии необходимо знать теорему о периметре и формулы для расчетов различных параметров равностороннего треугольника.

    [spoiler title=”источники:”]

    http://calcsbox.com/post/formula-perimetra-ravnostoronnego-treugolnika.html

    http://sprint-olympic.ru/uroki/geometrija/131613-perimetr-ravnostoronnego-treygolnika-formyla-i-primery-nahojdeniia.html

    [/spoiler]

    • Источник

    Выбирайте формулу в зависимости от известных величин.

    1. Как найти периметр треугольника, зная три стороны

    Просто посчитайте сумму всех сторон.

    Иллюстрация: Лайфхакер
    • P — искомый периметр;
    • a, b, c — стороны треугольника.

    2. Как найти периметр треугольника, зная его площадь и радиус вписанной окружности

    Умножьте площадь треугольника на 2.

    Разделите результат на радиус вписанной окружности.

    Иллюстрация: Лайфхакер
    • P — искомый периметр;
    • S — площадь треугольника;
    • r — радиус вписанной окружности.

    3. Как вычислить периметр треугольника, зная две стороны и угол между ними

    Сначала найдите неизвестную сторону треугольника с помощью теоремы косинусов:

    • Умножьте одну сторону на вторую, на косинус угла между ними и на 2.
    • Посчитайте сумму квадратов известных сторон и отнимите от неё число, полученное в предыдущем действии.
    • Найдите корень из результата.

    Теперь прибавьте к найденной стороне две ранее известные стороны.

    Иллюстрация: Лайфхакер
    • P — искомый периметр;
    • b, c — известные стороны треугольника;
    • ɑ — угол между известными сторонами;
    • a — неизвестная сторона треугольника.

    4. Как найти периметр равностороннего треугольника, зная одну сторону

    Умножьте сторону на 3.

    Иллюстрация: Лайфхакер
    • P — искомый периметр;
    • a — любая сторона треугольника (напомним, в равностороннем треугольнике все стороны равны).

    5. Как вычислить периметр равнобедренного треугольника, зная боковую сторону и основание

    Умножьте боковую сторону на 2.

    Прибавьте к результату основание.

    Иллюстрация: Лайфхакер
    • P — искомый периметр;
    • a — боковая сторона треугольника (в равнобедренном треугольнике боковые стороны равны);
    • b — основание треугольника (это сторона, которая отличается длиной от остальных).

    6. Как найти периметр равнобедренного треугольника, зная боковую сторону и высоту

    Найдите квадраты боковой стороны и высоты.

    Отнимите от первого числа второе.

    Найдите корень из результата и умножьте его на 2.

    Прибавьте к полученному числу две боковые стороны.

    Иллюстрация: Лайфхакер
    • P — искомый периметр;
    • a — боковая сторона треугольника;
    • h — высота (перпендикуляр, опущенный на основание треугольника со стороны противоположной вершины; в равнобедренном треугольнике высота делит основание пополам).

    7. Как вычислить периметр прямоугольного треугольника, зная катеты

    Найдите квадраты катетов и посчитайте их сумму.

    Извлеките корень из полученного числа.

    Прибавьте к результату оба катета.

    Иллюстрация: Лайфхакер
    • P — искомый периметр;
    • a, b — катеты треугольника (стороны, которые образуют прямой угол).

    8. Как найти периметр прямоугольного треугольника, зная катет и гипотенузу

    Посчитайте квадраты гипотенузы и катета.

    Отнимите от первого числа второе.

    Найдите корень из результата.

    Прибавьте катет и гипотенузу.

    Иллюстрация: Лайфхакер
    • P — искомый периметр;
    • a — любой катет прямоугольника;
    • c — гипотенуза (сторона, которая лежит напротив прямого угла).
    Источник

    Добавить комментарий