Эльбрус
Ученик
(207)
7 лет назад
Параллелепипед есть призма, все стороны которой являются параллелограммами. (Прямоугольный параллелепипед это фигура, стороны которой – прямоугольники.)
Если стороны основания имеют длину a и b тогда периметр основания есть P = 2a + 2b. Каждый параллелепипед имеет два основания, поэтому периметр двух оснований равен (2a + 2b).2 = 4a + 4b. Как мы знаем, параметр это сумма всех сторон. Таким образом, мы должны сложить четыре раза c
P = 4a + 4b + 4c
Seo Web
Профи
(865)
5 лет назад
Для того что бы вычислить периметр параллелепипеда необходимо знать длину его ребер a,b и c сходящихся к одной точки. Если нам известны указанные величины, для нас не составит труда вычислить периметр.
Периметр параллелепипеда рассчитывается по следующей формуле:
P=4a+4b+4c
Где P – периметр, a,b и c – длина ребер параллелепипеда.
или можно воспользоваться бесплатным онлайн калькулятором https://tamali.net/calculator/3d/parallelepiped/perimeter/
Объем, площадь и периметр прямоугольного параллелепипеда – онлайн
Объем, площадь и периметр прямоугольного параллелепипеда.
Прямоугольный параллелепипед — многогранник с шестью гранями, каждая из которых является в общем случае прямоугольником.
Противолежащие грани параллелепипеда равны. Рёбра параллелепипеда, сходящиеся в одной вершине взаимно перпендикулярны.
Объём прямоугольного параллелепипеда можно найти по формуле:
V=abc;
Площадь поверхности прямоугольного параллелепипеда равна:
S=2(ab+bc+ac);
Периметр параллелепипеда рассчитывается по следующей формуле:
P = 4a + 4b + 4c;
Объем, площадь и периметр прямоугольного параллелепипеда – калькулятор онлайн
Сторона a:
Сторона b:
Сторона c:
Найти:
V – Объем
S – Площадь
P – Периметр
Итого :
Поделиться в соц сетях:
Популярные сообщения из этого блога
Найти тангенс фи , если известен косинус фи
Калькулятор коэффициент мощности cos fi в tg fi Как найти тангенс фи, если известен косинус фи формула: tg φ = (√(1-cos²φ))/cos φ Калькулятор онлайн – косинус в тангенс cos φ: tg φ: Поделиться в соц сетях: Найти синус φ, если известен тангенс φ Найти косинус φ, если известен тангенс φ
Индекс Руфье калькулятор
Проба Руфье калькулятор онлайн. Первые упоминания теста относиться к 1950 году. Именно в это время мы находим первое упоминание доктора Диксона о “Использование сердечного индекса Руфье в медико-спортивном контроле”. Проба Руфье – представляет собой нагрузочный комплекс, предназначенный для оценки работоспособности сердца при физической нагрузке. Индекс Руфье для школьников и студентов. У испытуемого, находящегося в положении лежа на спине в течение 5 мин, определяют число пульсаций за 15 сек (P1); После чего в течение 45 сек испытуемый выполняет 30 приседаний. После окончания нагрузки испытуемый ложится, и у него вновь подсчитывается число пульсаций за первые 15 с (Р2); И в завершении за последние 15 сек первой минуты периода восстановления (Р3); Оценку работоспособности сердца производят по формуле: Индекс Руфье = (4(P1+P2+P3)-200)/10; Индекс Руфье для спортсменов Измеряют пульс в положении сидя (Р1); Спортсмен выполняет 30 глубоких приседаний в
Найти косинус фи (cos φ), через тангенс фи (tg φ)
tg фи=… чему равен cos фи? Как перевести тангенс в косинус формула: cos(a)=(+-)1/sqrt(1+(tg(a))^2) Косинус через тангенс, перевести tg в cos, калькулятор – онлайн tg φ: cos φ: ± Поделиться в соц сетях:
На прошлых занятиях мы рассматривали плоские фигуры.
В реальности же каждый предмет, какой бы он формы не был, занимает некоторую часть пространства.
Даже у самого тонкого листа бумаги имеется толщина.
Если взять стопку таких листов, то объем стопки бумаги будет хорошо заметен.
Эта информация доступна зарегистрированным пользователям
Раздел геометрии, в котором изучаются фигуры и их свойства в пространстве, называется стереометрией.
Слово стереометрия происходит от древнегреческого «стериос»- объемный, пространственный и «метрио»- измерять.
Базовыми фигурами в пространстве, как и на плоскости, является точка, прямая и плоскость, из которых образуются объемные геометрические фигуры, тела, пространства.
Геометрическое тело, состоящее из плоских многоугольников, называют многогранником.
Существует огромное множество многогранников: выпуклые, невыпуклые, правильные и т.д.
На данном уроке познакомимся с выпуклым прямоугольным многоугольником, который называется параллелепипед.
Эта информация доступна зарегистрированным пользователям
Выясним, как прямоугольный параллелепипед выглядит и из каких элементов он состоит.
Рассмотрим его свойства.
Научимся изображать данный многоугольник на плоскости и вычислять площадь его поверхности.
Разберем несколько примеров решения задач.
Каждый может себе представить и знает, как выглядят детские кубики.
С кубиками и конструктором из брусочков прямоугольной формы многие знакомы с раннего детства: строили домики, башенки, дороги, затем все это радостно рушили.
Эта информация доступна зарегистрированным пользователям
Всем известно, как выглядит коробка конфет или долька шоколада. Многие получали подарки в красивой красочной коробке с ярким бантом, читали книги с увлекательными рассказами и сказками.
Эта информация доступна зарегистрированным пользователям
Все эти знакомые вам предметы – это объемные тела, которые в реальности можно посмотреть, потрогать со всех сторон.
Если обратим внимание на форму, то заметим, что все изображенные объекты имеют некоторое сходство, они представляют собой прямоугольный параллелепипед.
Слово «параллелепипед» происходит от двух греческих слов: «параллелос» – идущие рядом и «опипедон» – плоскость.
Прямоугольный параллелепипед-это объемная геометрическая фигура, многогранник, состоящий из шести прямоугольников.
Прямоугольный параллелепипед – это пространственная фигура.
Плоские фигуры, такие как квадрат, прямоугольник, треугольник изобразить на плоскости легко, они являются её частью.
Любую объемную фигуру изобразить на плоскости затруднительно.
Многогранник необходимо изобразить так, чтобы была заметна объемность фигуры.
Для этого все линии многогранника, невидимые глазу, принято изображать на рисунке пунктирными линиями, а видимые – сплошными линиями.
Пунктирная линия дает возможность понять наблюдателю, как расположен многогранник и определить, откуда необходимо смотреть на него.
Если мы изобразим параллелепипед только сплошной линией, то на рисунке будут изображены различные четырехугольники, соединенные между собой, а объемного представления многоугольника данный рисунок не даст.
Эта информация доступна зарегистрированным пользователям
Даже если нам известно, что изображен прямоугольный параллелепипед, то все равно непонятно какой стороной расположен многогранник к наблюдателю.
Если невидимые линии на рисунке изобразить пунктирными линиями, то у фигуры сразу будет заметен объем.
Прямоугольный параллелепипед изображают так:
Эта информация доступна зарегистрированным пользователям
Прямоугольники, из которых состоит прямоугольный параллелепипед, называют гранями, причем противоположные грани его попарно равны.
Эта информация доступна зарегистрированным пользователям
Верхняя грань равна нижней, правая равна левой, передняя грань равна задней.
Грань, на которой стоит прямоугольный параллелепипед, называют нижним основанием, противоположную грань называют верхним основанием параллелепипеда.
Остальные четыре грани называют боковыми гранями.
Стороны граней называют ребрами параллелепипеда.
Эта информация доступна зарегистрированным пользователям
Концы ребер, т.е. вершины граней, называют вершинами параллелепипеда.
На рисунке вершины изображены точками.
Эта информация доступна зарегистрированным пользователям
Прямоугольный параллелепипед имеет три линейные величины (три измерения): ширину, длину и высоту.
Величину прямоугольного параллелепипеда определяют длинами трех ребер, исходящих из одной вершины.
Эта информация доступна зарегистрированным пользователям
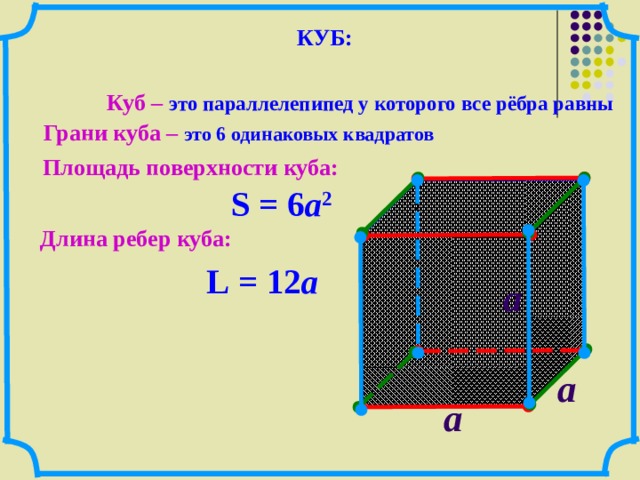
Если все три величины прямоугольного параллелепипеда равны, то такой параллелепипед называют кубом.
Другими словами, куб – это частный случай параллелепипеда.
Куб – это правильный многоугольник, состоящий из шести одинаковых квадратов.
Куб по-другому называют правильный гексаэдр (от греческого «hex»- шесть и «hedra»- грань).
Куб выглядит так:
Эта информация доступна зарегистрированным пользователям
Он имеет все те же элементы, что и прямоугольный параллелепипед.
Эта информация доступна зарегистрированным пользователям
Все шесть граней куба равны, следовательно, и все 12 ребер между собой равны.
Куб так же имеет 2 основания: нижнее, на котором он стоит, и противоположное ему – верхнее.
Остальные четыре его грани – это боковые грани.
Эта информация доступна зарегистрированным пользователям
Платоновские тела
|
Тетраэдр |
Гексаэдр |
Октаэдр |
Додекаэдр |
Икосаэдр |
|
|
Внешний вид |
 |
 |
 |
 |
 |
|
Число и вид граней |
4 правильных треугольника |
6 квадратов |
8 правильных треугольников |
12 правильных пятиугольников |
20 правильных треугольников |
|
Число ребер |
6 |
12 |
12 |
30 |
30 |
|
Число вершин |
4 |
8 |
6 |
20 |
12 |
|
Число ребер, сходящихся в вершине |
3 |
3 |
4 |
3 |
5 |
|
Символьное значение |
Огонь |
Земля |
Воздух |
Все сущее (все мироздание) |
Вода |
Эта информация доступна зарегистрированным пользователям
Если посмотреть вокруг, то мы можем заметить огромное множество объектов, имеющих форму прямоугольного параллелепипеда или напоминающих его форму.
Так, например, большинство зданий и помещений, шкаф (тумбочка), столешница, аквариум, коробка, кирпичи и многое другое представляют собой прямоугольный параллелепипед.
Эта информация доступна зарегистрированным пользователям
Такой многогранник имеет широкое применение в различных областях нашей жизни, и это неспроста:
1) прямоугольная форма параллелепипеда удобна для деления целого на части
2) объекты прямоугольной формы легко надстраивать и совмещать
3) прямоугольный параллелепипед является одним из самых устойчивых многогранников
Часто приходится определять площадь поверхности объекта, имеющего форму прямоугольного параллелепипеда.
Давайте разберемся, как и с помощью каких формул можно вычислить площадь его поверхности.
Допустим, у нас есть коробка, имеющая форму прямоугольного параллелепипеда.
Попробуем изобразить развертку данного геометрического тела.
Развертка параллелепипеда – это изображение его поверхности в виде плоской фигуры, составленной из двух равных оснований: прямоугольников и четырех боковых граней (прямоугольников, попарно равных друг другу).
Эта информация доступна зарегистрированным пользователям
Площадь этой развертки- это и есть площадь поверхности прямоугольного параллелепипеда.
Так как прямоугольный параллелепипед состоит из шести граней, имеющих форму прямоугольников, причем противоположные грани равны по величине, то площадь поверхности прямоугольного параллелепипеда будет равна сумме площадей всех его шести граней.
Пусть для нашего прямоугольного параллелепипеда три ребра, выходящие из одной вершины, имеют значения а, b, h.
Эта информация доступна зарегистрированным пользователям
а– ширина прямоугольного параллелепипеда
b– длина прямоугольного параллелепипеда
h– высота прямоугольного параллелепипеда
Найдем площадь всех граней.
Воспользуемся формулой для расчета площади прямоугольника: площадь прямоугольника равна произведению его ширины на длину.
Ребра, лежащие напротив ребер а, b, h, будут иметь такие же значения длины, так как противолежащие ребра прямоугольного параллелепипеда равны.
В таком случае получаем:
1) Площадь нижнего основания равна произведению (a ∙ b)
2) Площадь верхнего основания также равна произведению (a ∙ b)
3) Площадь левой боковой и правой боковой граней равны, как противолежащие, площадь каждой из них определяется произведением (b ∙ h)
4) Передняя и задняя боковые грани равны, а значение площади каждой из них будет определяться произведением (а ∙ h)
Сложим площади всех граней прямоугольного параллелепипеда, получим общую площадь его поверхности.
Эта информация доступна зарегистрированным пользователям
Упростим выражение, вынесем 2 за скобку.
Формула площади поверхности прямоугольного параллелепипеда будет выглядеть так:
Эта информация доступна зарегистрированным пользователям
Площадь двух оснований прямоугольного параллелепипеда (это два прямоугольника) найдем по формуле:
Sосн = 2 (a ∙ b).
Площадь боковой поверхности прямоугольного параллелепипеда можно найти по формуле:
Sбок = 2h ∙ (a + b).
В нашем случае а, b– это стороны основания, h– это высота прямоугольного параллелепипеда (боковое ребро).
Так как основанием прямоугольного параллелепипеда является прямоугольник, то периметр основания прямоугольного параллелепипеда определяется равенством
Роснов = 2 ∙ (a + b).
Подставим Роснов в формулу Sбок = 2h ∙ (a + b) вместо выражения 2 ∙ (a + b).
Тогда площадь боковой поверхности можно найти так:
Sбок = Роснов ∙ h.
Определим площадь поверхности куба.
Известно, что куб – это прямоугольный параллелепипед, поверхность которого состоит из шести одинаковых граней, имеющих форму квадрата.
Чтобы найти площадь поверхности куба, необходимо сложить площади всех его граней.
Площадь одной грани куба найдем по формуле площади квадрата:
S = a2
а– это сторона квадрата (ребро куба).
Так как все 6 граней куба представляют собой равные по площади квадраты, следовательно, чтобы найти площадь всей поверхности куба, необходимо площадь одной грани умножить на их количество.
Формула площади поверхности куба выглядит так:
Эта информация доступна зарегистрированным пользователям
Рассмотрим решение нескольких практических задач.
В процессе любого строительства или ремонта очень часто встает вопрос о том, сколько необходимо потратить строительного и отделочного материала или как рассчитать расход краски.
Задача №1.
Какое количество краски понадобится, чтобы полностью покрасить бак прямоугольной формы?
Ширина бака 2 метра, длина 3 метра, высота 1 метр.
Известно, что на 1 м2 расходуется 200 г краски.
Эта информация доступна зарегистрированным пользователям
Чтобы рассчитать количество краски, которое нужно затратить на покраску бака, необходимо определить площадь окрашиваемой поверхности, затем, зная норму расхода краски на единицу площади, можно рассчитать расход краски на всю окрашиваемую поверхность.
Пусть m1– масса краски, которая расходуется на 1 м2
m2– масса краски, которая необходима для покраски всего бака.
Эта информация доступна зарегистрированным пользователям
Задача №2
Сколько квадратных метров стекла понадобится на изготовление аквариума кубической формы длиной 100 см?
Эта информация доступна зарегистрированным пользователям
Для вычисления площади поверхности аквариума в квадратных метрах необходимо длину аквариума перевести из сантиметров в метры.
Вспомним, 1 м = 100 см.
Эта информация доступна зарегистрированным пользователям
Если бы аквариум необходимо было изготовить только из боковых стенок и основания, то из стекла пришлось бы вырезать всего 5 квадратных граней.
В таком случае формула для вычисления площади поверхности аквариума приняла бы вид
S = 5 а2.
Задача №3
Хозяйка решила покрасить стены в комнате.
Вычислите площадь поверхности стен комнаты, в которой имеется дверной проем площадью 2 м2 и оконный проем площадью 1 м2.
Комната имеет форму прямоугольного параллелепипеда.
Ширина комнаты 3 метра, длина комнаты 4 метра, высота комнаты 3 метра.
Эта информация доступна зарегистрированным пользователям
Пусть Sc– общая площадь стен комнаты.
Sд– площадь дверного проема.
Sо– площадь оконного проема.
S– площадь стен комнаты за исключением площади дверного и оконного проемов.
Эта информация доступна зарегистрированным пользователям
Читайте также
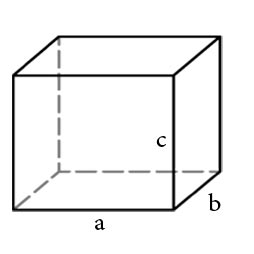
При помощи нашего калькулятора вы легко сможете узнать периметр прямоугольного параллелепипеда.
| Длина ребра а: | |
| Длина ребра b: | |
| Длина ребра c: | |
Для того что бы вычислить периметр параллелепипеда необходимо знать длину его ребер a,b и c сходящихся к одной точки. Если нам известны указанные величины, для нас не составит труда вычислить периметр.
Периметр параллелепипеда рассчитывается по следующей формуле:
P=4a+4b+4c
Где P – периметр, a,b и c – длина ребер параллелепипеда.
Производная в задачах на прямоугольный параллелепипед 10 класс онлайн-подготовка на Ростелеком Лицей
Тема: Производная
Урок: Производная в задачах на прямоугольный параллелепипед
1. Задача 1 на прямоугольный параллелепипед
Рассматриваются всевозможные прямоугольные параллелепипеды, основания которых квадраты, а каждая из боковых граней имеет периметр . Найти среди них параллелепипед с наибольшим объемом и вычислить его объем.
Решение.
Напомним, прямоугольным называется параллелепипед, у которого в основании лежит прямоугольник, и боковые ребра перпендикулярны к плоскости основания.
Нам важны три измерения этого параллелепипеда. Так как в основании лежит квадрат, то его стороны обозначим через , третье измерение параллелепипеда обозначим через (см. рис. 1).
Рис. 1. Прямоугольный параллелепипед и его измерения.
Объем любого прямоугольного параллелепипеда – это произведение трех его измерений. Надо найти такой параллелепипед, чтобы его объем был максимальным (смотрим прямоугольный параллелепипед формулы), то есть
. Между и есть связь. Сказано, что или . Заметим, что , .
Мы бы могли решить эту задачу, если бы функция зависела от одной переменной, а она зависит от двух переменных и . Одну из них можно выразить через связь . Отсюда . Подставим полученное выражение в функцию: . Теперь задачу можно свести к типовой задаче: найти на отрезке .
1) Найдем производную
– критические точки.
Достаточно сравнить значение функции на концах отрезка и в тех критических точках, которые попадают на данный отрезок. Продемонстрируем, что точка — точка максимума. Для этого проанализируем знак производной (см. рис.2).
Рис. 2. Интервалы знакопостоянства производной.
Найдем значение функции в точках:
Если , тогда . Найдем объем .
Итак, мы искали такой прямоугольный параллелепипед, в основании которого лежит квадрат, и периметр боковой грани равен 6.
2. Задача 2 на прямоугольный параллелепипед
Рассматриваются всевозможные прямоугольные параллелепипеды, объем каждого из которых равен , а основаниями являются квадраты. Найти среди них параллелепипед с наименьшим периметром боковой грани и вычислить этот периметр.
Рис. 3. Прямоугольный параллелепипед и егобоковые грани и измерения.
Решение.
Так как в основании параллелепипеда – квадрат, то одна его сторона равна и вторая – , боковое ребро – (см. рис.3). Известно, что объем этих параллелепипедов -. Надо найти параллелепипед с наименьшим периметром боковой грани. Периметр боковой грани равен . Этот периметр должен быть наименьшим: .
Найдем производную .
, отсюда и — критические точки.
Найдем интервалы знакопостоянства производной и посмотрим является ли точка точкой минимума (см. рис.4).
Рис. 4. Интервалы знакопостоянства производной.
Таким образом, точка является точкой минимума. Напомним, мы должны найти такую точку, при которой периметр будет наименьшим. Выяснили, что на всем промежутке значение функции в точке является наименьшим, так как на промежутке функция убывает, а на промежутке – возрастает. Точка экстремума на промежутке — единственная.
Найдем . И, наконец, найдем .
Итак, требовалось найти такой параллелепипед, у которого наименьший периметр боковой грани и вычислить этот периметр. Параллелепипед нашли, он имеет измерения . Наименьшее значение периметра боковой грани равно .
3.

Итак, мы рассмотрели стереометрические задачи на экстремум, которые решаются с помощью производной. Решили две взаимно обратные задачи на прямоугольный параллелепипед с использованием формул и боковых сторон параллелепипеда. В первой задаче нужно было найти максимальное значение объема, а во второй – наименьшее значение периметра в прямоугольном параллелепипеде. Эти задачи, как и в планиметрии, решаются следующим образом: составляется нужная функция, она оказывается функцией двух переменных, выписываются геометрические связи, они позволяют выразить одну переменную через другую и получить функцию только от одной переменной. Дальше применяя производную, можно успешно решить задачу.
Список рекомендованной литературы по теме «Прямоугольный параллелепипед формулы», «Боковые стороны параллелепипеда»
1. Алгебра и начала анализа, 10 класс (в двух частях).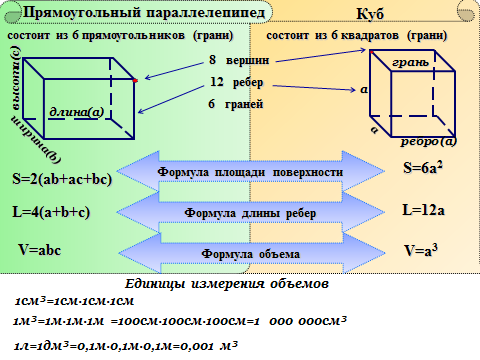
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.
4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.
6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.
7. ЗвавичЛ.И., Шляпочник Л.Я., Чинкина Алгебра и начала анализа. 8-11 кл.: Пособие для школ и классов с углубленным изучением математики (дидактические материалы).
8. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
9. Карп А.П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
10. Глейзер Г.И. История математики в школе. 9-10 классы (пособие для учителей).-М.: Просвещение, 1983
Дополнительные веб-ресурсы
1. Интернет-портал Mathematics.ru (Источник).
2. Портал Естественных Наук (Источник).
3. Интернет-портал Exponenta.ru (Источник).
Сделай дома — решение задач на прямоугольный параллелепипед, как найти сторону прямоугольного параллелепипеда
№ 46.59, 46.50 (Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.)
Как найти площадь поверхности прямоугольного параллелепипеда: формула
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.
В данной публикации мы рассмотрим, как можно вычислить площадь поверхности прямоугольного параллелепипеда и разберем пример решения задачи для закрепления материала.
- Формула вычисления площади
- Пример задачи
Формула вычисления площади
Площадь (S) поверхности прямоугольного параллелепипеда вычисляется следующим образом:
S = 2 (ab + bc + ac)
Формула получена следующим образом:
- Гранями прямоугольного параллелепипеда являются прямоугольники, причем противоположные грани равны между собой:
- два основания: со сторонами a и b;
- четыре боковые грани: со стороной a/b и высотой c.
- Сложив площади всех граней, каждая из которых равна произведению сторон разной длины, получаем: S = ab + ab + bc + bc + ac + ac = 2 (ab + bc + ac).
Пример задачи
Вычислите площадь поверхности прямоугольного параллелепипеда, если известно, что его длина равна 6 см, ширина – 4 см, а высота – 7 см.
Решение:
Воспользуемся формулой выше, подставив в нее известные значения:
S = 2 ⋅ (6 см ⋅ 4 см + 6 см ⋅ 7 см + 4 см ⋅ 7 см) = 188 см2.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Изучите концепцию, формулу, сравнение, примеры
0
Сохранить
Скачать публикацию в формате PDF
Периметр куба равен 12а в единицах.
Периметр куба
Можно считать, что куб состоит из двумерных фигур, поскольку каждая из его шести граней представляет собой квадрат. У него восемь вершин, шесть граней и двенадцать ребер. Эти двенадцать ребер всегда параллельны каждому из его противоположных ребер. Следовательно, периметр куба должен быть равен общей сумме его ребер или длин.
Рассмотрим рисунок выше,
Каждая сторона равна «a» единицам, всего 12 сторон,
Следовательно, периметр куба (P) = 12 x a = 12 a.
Периметр куба Формула
Формула для Периметра куба дается следующим образом:
Периметр куба (P) = 12 x a (единиц).
Где a = длина каждой стороны куба.
Периметр куба и площадь поверхности куба
Давайте кратко обсудим площадь поверхности куба и чем она отличается от периметра.
| Периметр куба | Площадь поверхности куба |
| Периметр – это сумма длин всех сторон куба, умноженная на 12. | Принимая во внимание, что площадь поверхности куба равна сумме площадей всех его граней. |
| Мы знаем, что куб имеет 6 граней в форме квадрата. Следовательно, площадь поверхности куба = 6 x площадь поверхности квадратной грани = 6 x a². | Площадь поверхности квадрата равна квадрату его длины, определяемой по формуле Площадь поверхности квадрата = a², где «a» — длина каждой из его сторон. |
| Периметр куба равен сумме длин каждой из его сторон | Площадь поверхности равна сумме площадей каждой из его граней. |
Периметр решенного куба Примеры
Пример 1 . Длина ребер в кубе равна 8,5 см каждое. Каков будет периметр куба?
Решение 1.
Приведены данные,
Длина каждого ребра в кубе = 8,5см.
Формула Периметр куба = 12 x a.
= 12 х 8,5 см.
= 102 см.
Периметр куба равен 102 см.
Пример 2 . Площадь поверхности куба 64 м², какой длины будет его ребро?
Решение 2.
Приведены данные,
Площадь поверхности куба = 64 м²
Формула площади поверхности куба = 6 х а², где а — длина каждой из его сторон.
64 = 6 x а²
а² = 64 / 6
а² = 10,66
а = 3,26 см.
Длина каждой стороны куба равна 3,26 см.
Пример 3 . Найдите периметр и площадь поверхности куба, если длина каждой из его сторон равна 5 см.
Решение 3,
Приведенные данные,
Длина каждой стороны куба (а) = 5 см
Периметр куба = 12 х а = 12 х 5 = 60 см.
Площадь поверхности куба = 6 x a² = 6 x 25
= 150 см².
Следовательно, периметр данного куба равен 60 см, а площадь его поверхности 150 см².
Надеюсь, эта статья была информативной и помогла вам в учебе и подготовке к экзаменам. Оставайтесь с нами в приложении Testbook, чтобы узнать больше об обновлениях и темах, связанных с математикой и другими подобными предметами. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний о связанных экзаменах.
Часто задаваемые вопросы о периметре куба
В.1 Как преобразовать периметр куба в сторону?
Ответ 1 Периметр куба определяется по формуле Периметр (P) = 12 x a, где «a» — длина каждой стороны. Следовательно, применяя формулу для данного периметра куба, мы можем вычислить длину его стороны.
Q.2 Чему равен периметр прямоугольного параллелепипеда?
Ответ 2 Периметр прямоугольного параллелепипеда определяется по формуле 4 x (L+B+H), где L = длина куба, B = ширина куба и H = высота куба.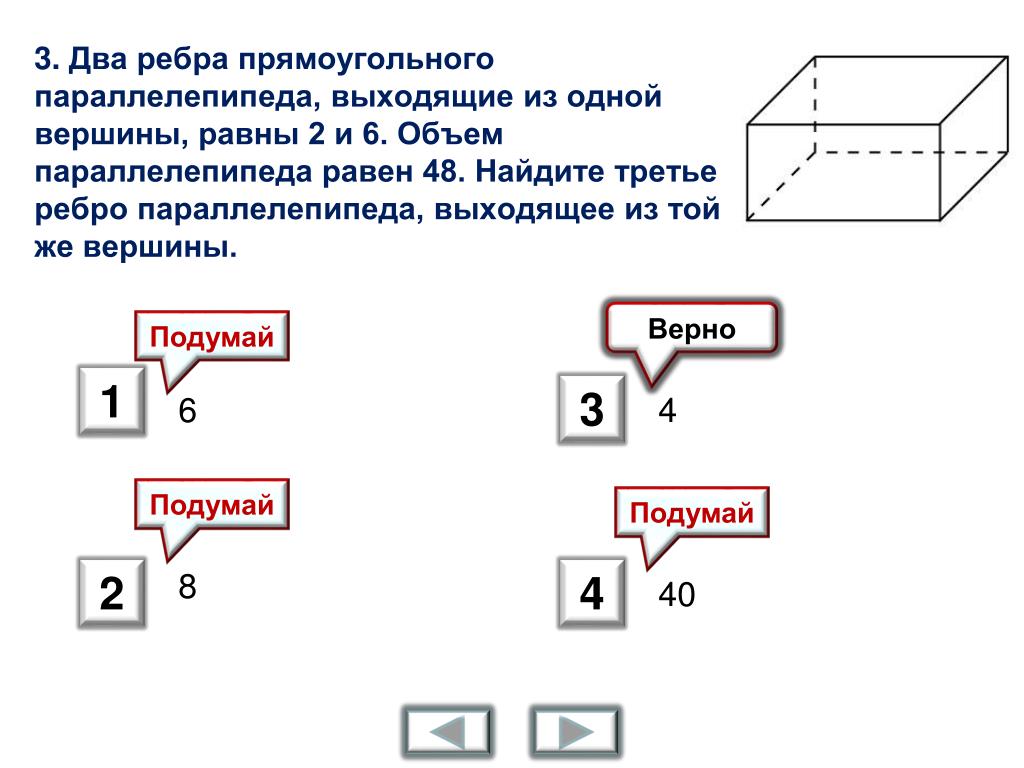
Q.3 Каков периметр одной грани куба?
Ответ 3 Одна грань куба в основном представляет собой квадрат, а квадрат имеет четыре ребра, следовательно, периметр одной грани куба равен 4 x a, где «a» — длина стороны.
Q.4 Как найти основание куба?
Ответ 4 Основание куба — квадрат, поэтому его площадь основания будет равна а², где «а» — длина каждой стороны.
Q.5 Как найти периметр куба?
Ответ 5 Периметр куба определяется по формуле Периметр (P) = 12 x a, где «a» — длина каждой стороны.
Скачать публикацию в формате PDF
Еще на testbook.com
| Равномерное распределение в вероятности: типы, формулы и примеры |
| Периметр равнобедренного треугольника: изучите понятие, родственную формулу и решенные примеры. |
| Обратная связь: изучите определение, теорему, область определения и диапазон на примерах! |
Сумма N терминов в AP: изучите концепцию, доказательства и решенные примеры. |
| Однородное дифференциальное уравнение: изучите типы определений на примерах |
Функция — Как вычислить периметр прямоугольного параллелепипеда?
Шаги этой задачи относительно просты.
- Получить длину, ширину и ширину.
- Убедитесь, что значения находятся в требуемых пределах.
- Вычислите периметр.
- Укажите расчетный периметр или длину, в зависимости от того, насколько педантичен человек, пишущий эти требования.
Номер четыре, вероятно, является самой сложной частью этой задачи, и вам следует связаться с человеком, составившим требования, чтобы убедиться, что вывод : возврат длины кубоида на самом деле является опечаткой и что вы должны вернуть периметр кубоида.
В этом примере я предполагаю, что это вопрос с подвохом, и укажу длину; однако, если это не вопрос с подвохом, а опечатка, вам следует заменить переменную длины (LE) на переменную периметра (PE) в строке вывода (80).
10 ЕСЛИ НЕТ (LE < 1 ИЛИ LE > 100 ИЛИ BR < 1 ИЛИ BR > 100 ИЛИ WI < 1 ИЛИ WI > 100), ТО 60 20 ВВОД "ДЛИНА, ШИРИНА, ШИРИНА"; LE, BR, WI 30 ЕСЛИ LE < 1 ИЛИ BR < 1 ИЛИ WI < 1, ТОГДА НАПЕЧАТАЙТЕ «ВЫ ВВЕЛИ»: НАПЕЧАТАЙТЕ «MICROVERSE. ПОЖАЛУЙСТА, УБЕДИТЕСЬ, ЧТО»: 40 ЕСЛИ LE > 100 ИЛИ BR > 100 ИЛИ WI > 100, ТОГДА ВЫБЕРИТЕ ГРАНИЦЫ: ВЫШИТЕ "ИЗВЕСТНУЮ ВСЕЛЕННУЮ". " 50 ПЕРЕЙТИ К 10 60 PE = ЛЭ + БР + ВИ 70 ПЭ=ПЭ*4 80 PRINT "ДЛИНА КУБОИДА:";LE 90 КОНЕЦ
Бейсик никогда не был известен своей удобочитаемостью, и даже эта короткая программа, вероятно, трудна для понимания. Вот та же программа в более читабельной форме:
цикл while (%length% < 1 или %length% > 100 или %breadth% < 1 или %breadth% > 100 или %width% < 1 или %width% > 100)
ввод "Длина, Ширина, Ширина"; %длина%, %ширина%, %ширина%
выключатель
case (%length% < 1 или %breadth% < 1 или %width% < 1)
Wrap Вы вошли в микровселенную. Пожалуйста, убедитесь, что все размеры составляют не менее 1 единицы. case (%length% > 100 или %breadth% > 100 или %width% > 100)
wrap Вы покинули пределы известной вселенной. Пожалуйста, убедитесь, что все размеры не превышают 100 единиц.
концевой выключатель
концевая петля
%периметр% = %длина% + %ширина% + %ширина%
%периметр% *= 4
print "Длина прямоугольного параллелепипеда:";%length%
case (%length% > 100 или %breadth% > 100 или %width% > 100)
wrap Вы покинули пределы известной вселенной. Пожалуйста, убедитесь, что все размеры не превышают 100 единиц.
концевой выключатель
концевая петля
%периметр% = %длина% + %ширина% + %ширина%
%периметр% *= 4
print "Длина прямоугольного параллелепипеда:";%length%
Здесь используется SuperBASIC не в качестве рекомендации (если, что маловероятно, BASIC, который вы используете, не находится на цветном компьютере TRS-80), а просто потому, что я знаком с этим препроцессором BASIC. Эти две программы в чем-то эквивалентны в том смысле, что я написал более читаемый код, а затем использовал скрипт для перевода его на BASIC.
Вы можете увидеть шаги, описанные выше: введите размеры прямоугольного параллелепипеда; убедиться, что размеры находятся в требуемых пределах; и либо зациклить
обратно на запрос ввода , если они не равны, или вычислить периметр и напечатать длину, если они есть.


 case (%length% > 100 или %breadth% > 100 или %width% > 100)
wrap Вы покинули пределы известной вселенной. Пожалуйста, убедитесь, что все размеры не превышают 100 единиц.
концевой выключатель
концевая петля
%периметр% = %длина% + %ширина% + %ширина%
%периметр% *= 4
print "Длина прямоугольного параллелепипеда:";%length%
case (%length% > 100 или %breadth% > 100 или %width% > 100)
wrap Вы покинули пределы известной вселенной. Пожалуйста, убедитесь, что все размеры не превышают 100 единиц.
концевой выключатель
концевая петля
%периметр% = %длина% + %ширина% + %ширина%
%периметр% *= 4
print "Длина прямоугольного параллелепипеда:";%length%