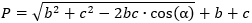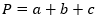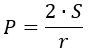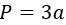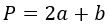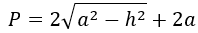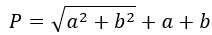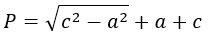Как найти периметр основания в треугольнике формула

Как найти периметр основания в треугольнике формула

Периметр треугольника калькулятор онлайн умеет вычислять периметр восемью способами:

  1. По трем сторонам.
  2. По площади и радиусу вписанной окружности.
  3. По двум сторонам и углу между ними.
  4. По стороне равностороннего треугольника.
  5. По боковой стороне и основанию равнобедренного треугольника.
  6. По боковой стороне и высоте равнобедренного треугольника.
  7. По катетам прямоугольного треугольника.
  8. По одному катету и гипотенузе прямоугольного треугольника.

Сделав расчет периметра на этом онлайн калькуляторе Вы получите не только ответ, но и детальное, пошаговое решение с выводом формул и промежуточных действий.

Треугольник

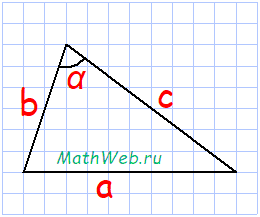
Треугольник – это геометрическая фигура, состоящая из трех точек (вершины треугольника), не лежащих на одной прямой, соедененных тремя отрезками (стороны треугольника).
Формула периметра треугольника: Формула периметра треугольника по двум сторонам и углу между ними.
где b,c – стороны треугольника, α° – угол между ними.

Решение:

P = √b2 + с2 – 2bc·cos(α°) + b + c

= √82 + 152 – 2·8·15·cos(60°) + 8 + 15

= √64 + 225 – 120 + 23

= √169 + 23

= 13 + 23

=

36

Ответ: Периметр треугольника со сторонами b = 8, c = 15 и углом между ними α° = 60 равен 36

Периметр треугольника- это сумма трех сторон.
Периметр может быть найден и по другим формулам, вывод которых основан на поиске длины неизвестной стороны.
 

Как найти периметр треугольника?

Найти периметр треугольника очень просто на нашем онлайн калькуляторе. Так же периметр может быть найден самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.

1) По трем сторонам


где a,b,c – стороны треугольника.

2) По площади и радиусу вписанной окружности


где S – площадь треугольника, r – радиус вписанной окружности.

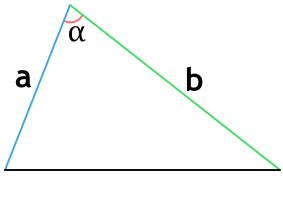
3) По двум сторонам и углу между ними


где b,c – стороны треугольника, α° – угол между ними.

4) По стороне равностороннего треугольника


где a – сторона равностороннего треугольника.

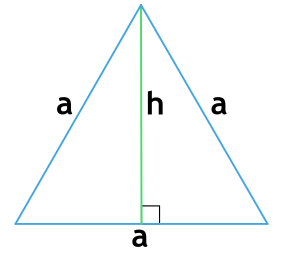
5) По боковой стороне и основанию равнобедренного треугольника


где a – боковая сторона и b – основание равнобедренного треугольника.

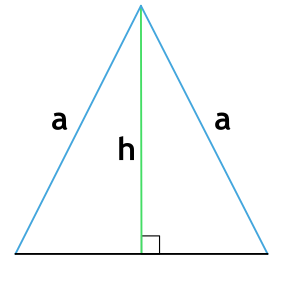
6) По боковой стороне и высоте равнобедренного треугольника


где a – боковая сторона и h – высота равнобедренного треугольника.

7) По катетам прямоугольного треугольника


где a,b – катеты прямоугольного треугольника.

8) По одному катету и гипотенузе прямоугольного треугольника.


где а – катет и с – гипотенуза прямоугольного треугольника.

Скачать все формулы в формате Word

Источник

Формулы периметра треугольника

Как найти периметр любого треугольника? Существует
множество способов сделать это, но мы расскажем про
основные. В этой статье вы узнаете, как найти периметр
любого треугольника через известные величины, по формулам.

Ⅰ. Через площадь и радиус вписанной окружности

Известно: площадь и радиус вписанной окружности треугольника.

Чтобы найти периметр любого треугольника,
нужно две площади треугольника разделить
на радиус вписанной окружности.

Как видим, для этой формулы нужно знать всего
лишь радиус вписанной окружности и площадь.

Ⅱ. Через три стороны

Известно: три стороны треугольника.

Чтобы найти периметр любого треугольника,
нужно сложить все стороны треугольника.
Результатом и будет периметр.

Это самая простая формула.

Ⅲ. Через Теорему Косинусов

Известно: две стороны и угол между ними.

Чтобы найти периметр любого треугольника,
нужно для начала найти третью сторону треугольника,
затем косинус угла, если косинус неизвестен.

Это формулу удобней применить,
если вам известны две стороны
и косинус между ними.

Как найти периметр треугольника

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение

Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской буквой P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах и ходе решении.

Важно, чтобы все параметры были переданы в одной единице длины, иначе мы не сможем подсчитать результат. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

В чем измеряется периметр:

Как узнать периметр треугольника

Рассмотрим какие существуют формулы, и при каких известных исходных данных их можно применять.

Если известны три стороны, то периметр треугольника равен их сумме. Этот способ проходят во втором классе.

P = a + b + c, где a, b, c — длина стороны.

Если известна площадь и радиус вписанной окружности:

P = 2 * S : r, где S — площадь, r — радиус вписанной окружности.

Если известны две стороны и угол между ними, вычислить периметр треугольника можно так:

P = √ b 2 + с 2 – 2 * b * с * cosα + (b + с), где b, с — известные стороны, α — угол между известными сторонами.

Если известна одна сторона в равностороннем треугольнике:

P = 3 * a, где a — длина стороны.

Все стороны в равносторонней фигуре равны.

Если известна боковая сторона и основание в равнобедренном треугольнике:

P = 2 * a + b, где a — боковая сторона, b — основание.

Боковые стороны в равнобедренной фигуре равны.

Если известна боковая сторона и высота в равнобедренном треугольнике:

P = 2 * (√ a 2 + h 2 ) + 2 * a, где a — боковая сторона, h — высота.

Высотой принято называть отрезок, который вышел из вершины и опустился на основание. В равнобедренной фигуре высота делит основание пополам.

Если известны катеты в прямоугольном треугольнике:

P = √ a 2 + b 2 + (a + b), где a, b — катеты.

Катет — одна из двух сторон, которые образуют прямой угол.

Если известны катет и гипотенуза в прямоугольном треугольнике:

P = √ c 2 – a 2 + (a + c), где a — любой катет, c — гипотенуза.

Гипотенуза — сторона, которая лежит напротив прямого угла.

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Периметры фигур. Периметр треугольника.

Периметр геометрической фигуры – суммарная длина границ плоской геометрической фигуры. Периметр

имеет ту же размерность величин, что и длина.

Треугольник – это многоугольник с тремя сторонами. Стороны треугольника обозначаются малыми

буквами, соответствующими обозначению противоположных вершин.

Периметр треугольника равен сумме длин его сторон, общая формула:

где a,b,c – длины сторон треугольника

Формула периметра треугольника для треугольника АВС:

Периметр равностороннего треугольника.

Чтобы найти периметр равностороннего треугольника (или найти периметр правильного

треугольника), нужно знать его сторону.

В общем случае для нахождения периметра треугольника используют формулу:

Поскольку в равностороннем треугольнике все три стороны равны, формула упрощается:

Таким образом, периметр равностороннего треугольника находится по такой формуле:

где а — длина его стороны.

Периметр равнобедренного треугольника.

Чтобы найти периметр равнобедренного треугольника, нужно знать всего две его стороны — основание

и боковую сторону.

Поскольку у равнобедренного треугольника две стороны равны (боковые), найти периметр

равнобедренного треугольника можно по такой формуле:

То есть, периметр равнобедренного треугольника равен сумме длин основания и

[spoiler title=”источники:”]

http://skysmart.ru/articles/mathematic/perimetr-treugolnika

http://www.calc.ru/Perimetry-Figur-Perimetr-Treugolnika.html

[/spoiler]

Источник

Чтобы найти периметр равнобедренного треугольника, нужно знать всего две его стороны — основание и боковую сторону.

В общем случае формула для нахождения периметра треугольника выглядит так:

    [P = a + b + c,]

где a, b и c — длины сторон треугольника.

perimetr ravnobedrennogo treugolnika

Поскольку у равнобедренного треугольника

две стороны равны (боковые),

формулу можно упростить:

    [P = a + b + b = a + 2b.]

Таким образом, периметр равнобедренного треугольника равен сумме длин основания и удвоенной боковой стороны:

    [P = a + 2b.]

perimetr treugolnika abc

Соответственно, периметр равнобедренного треугольника ABC можно найти по формуле:

    [{P_{Delta ABC}} = AC + 2 cdot AB]

(здесь AC — основание, AB — боковая сторона).

Примеры.

1) Найти периметр равнобедренного треугольника, если его основание равно 4 см, а боковая сторона — 9 см.

Решение:

Здесь а=4 см, b=9 см. По формуле Р=а+2b имеем: P=4+2∙9=22 (cм).

2) Периметр равнобедренного треугольника равен 170 см, а его основание — 60 см. Найти боковую сторону треугольника.

Решение:

Здесь а=60 см, Р=170 см. По формуле Р=а+2b, 2b=Р-а, b=(Р-а):2, b=(170-60):2=55 (см).

Задача нахождения периметра равностороннего треугольника решается еще проще. Её мы рассмотрим в следующий раз.

Источник

Периметр треугольника по трем сторонам

{P=a+b+c}

Чтобы найти периметр треугольника необходимо сложить длины трех его сторон. Однако, существует множество других формул, которые позволяют рассчитать периметр треугольника. На странице мы собрали самые известные формулы для расчета периметра треугольника, а также удобный калькулятор.

Содержание:
  1. калькулятор периметра треугольника
  2. формула периметра треугольника через стороны
  3. формула периметра треугольника по средним линиям
  4. формула периметра треугольника по двум сторонам и углу между ними
  5. формула периметра прямоугольного треугольника по катету и гипотенузе
  6. формула периметра прямоугольного треугольника по катетам
  7. формула периметра прямоугольного треугольника по гипотенузе и прилежащему углу
  8. формула периметра прямоугольного треугольника по катету и прилежащему углу
  9. формула периметра прямоугольного треугольника по катету и противолежащему углу
  10. формула периметра равнобедренного треугольника по боковой стороне и высоте
  11. формула периметра равнобедренного треугольника по основанию и высоте
  12. формула периметра равнобедренного треугольника по боковой стороне и основанию
  13. формула периметра равностороннего треугольника по высоте
  14. формула периметра равностороннего треугольника через площадь вписанной окружности
  15. примеры задач

Треугольник – геометрическая фигура, состоящая из трех точек, которые не лежат на одной прямой, и трех отрезков, которые попарно соединяют эти точки.

Формула периметра треугольника через стороны

Периметр треугольника через стороны

{P = a+b+c}

a, b и c – стороны треугольника

Формула периметра треугольника по средним линиям

Средняя линия треугольника — отрезок, который соединяет середины двух сторон.

Периметр треугольника по средним линиям

{P=2a+2b+2c}

a, b и c – средние линии треугольника

Формула периметра треугольника по двум сторонам и углу между ними

Периметр треугольника по двум сторонам и углу между ними

{P=a+b+sqrt{a^2+b^2-2ab cdot cos(alpha)}}

a и b – стороны треугольника

α – угол между сторонами a и b

Формула периметра прямоугольного треугольника по катету и гипотенузе

Прямоугольный треугольник — это треугольник, в котором один угол прямой (90 градусов).

Периметр прямоугольного треугольника по катету и гипотенузе

{P = a+c+sqrt{c^2-a^2}}

a – катет прямоугольного треугольника

c – гипотенуза прямоугольного треугольника

Формула периметра прямоугольного треугольника по катетам

Периметр прямоугольного треугольника по катетам

{P = a+b+sqrt{a^2+b^2}}

a и b – катеты прямоугольного треугольника

Формула периметра прямоугольного треугольника по гипотенузе и прилежащему углу

Периметр прямоугольного треугольника по гипотенузе и прилежащему углу

{P=csin(alpha)+ccos(alpha)+c}

c – гипотенуза прямоугольного треугольника

α – прилежащий к гипотенузе угол

Формула периметра прямоугольного треугольника по катету и прилежащему углу

Периметр прямоугольного треугольника по катету и прилежащему углу

{P=a \tg(alpha)+a+dfrac{a}{cos(alpha)}}

a – катет прямоугольного треугольника

α – прилежащий к катеру угол

Формула периметра прямоугольного треугольника по катету и противолежащему углу

Периметр прямоугольного треугольника по катету и противолежащему углу

{P=a+dfrac{a}{\tg(alpha)}+dfrac{a}{sin(alpha)}}

a – катет прямоугольного треугольника

α – противолежащий к катеру угол

Формула периметра равнобедренного треугольника по боковой стороне и высоте

Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине.

Периметр равнобедренного треугольника по боковой стороне и высоте

{P = 2a+2sqrt{a^2-h^2}}

a – боковая сторона равнобедренного треугольника

h – высота равнобедренного треугольника

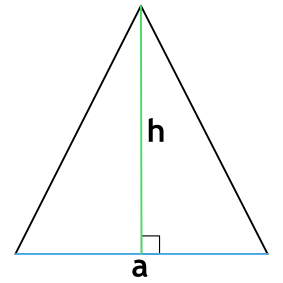
Формула периметра равнобедренного треугольника по основанию и высоте

Периметр равнобедренного треугольника по основанию и высоте

{P = a+2sqrt{Big( Big(dfrac{a}{2} Big)^2+h^2 Big)}}

a – основание равнобедренного треугольника

h – высота равнобедренного треугольника

Формула периметра равнобедренного треугольника по боковой стороне и основанию

Периметр равнобедренного треугольника по боковой стороне и основанию

{P=2b+a}

a – основание равнобедренного треугольника

b – боковая сторона равнобедренного треугольника

Формула периметра равностороннего треугольника по высоте

Равносторонний треугольник —треугольник, у которого все стороны равны.

Периметр равностороннего треугольника по высоте

{P=2sqrt{3}h}

h – высота равностороннего треугольника

Формула периметра равностороннего треугольника через площадь вписанной окружности

Периметр равностороннего треугольника через площадь вписанной окружности

{P = 6sqrt{dfrac{3S}{pi}}}

S – площадь вписанной в равносторонний треугольник окружности

Примеры задач на нахождение периметра треугольника

Задача 1

Найдите периметр треугольника, если его средние линии равны 6см 9см и 10см.

Решение

Для решения задачи применим формулу №2. Подставим в нее длины средних линий и произведем вычисления.

P = 2a+2b+2c = 2 cdot 6 + 2 cdot 9 + 2 cdot 10 = 12 + 18 + 20 = 50 : см

Ответ: 50 см

Ответ проверим с помощью калькулятора .

Задача 2

Найдите периметр треугольника со сторонами 14см, 17см и 17см.

Решение

А для этой задачи подойдет первая формула.

P = a+b+c = 14 + 17 + 17 = 48 : см

Если обратить внимание на то, что у треугольника в условии две стороны имеют одинаковую длину, то можно понять, что данный треугольник равнобедренный. И тогда задачу можно решить используя формулу для равнобедренного треугольника.

P=2b+a = 2 cdot 17 + 14 = 34 + 14 = 48 : см

Ответ: 48 см

Проверим ответ по первой и второй формуле.

Задача 3

Найдите периметр прямоугольного треугольника, если его катеты равны 12см и 16см.

Решение

Воспользуемся подходящей формулой.

P = a+b+sqrt{a^2+b^2} = 12+16+sqrt{12^2+16^2} = 28+sqrt{144+256} = 28+sqrt{400} = 28+20 = 48 : см

Ответ: 48 см

Полученный результат удобно проверить с помощью калькулятора .

Задача 4

Найдите периметр равнобедренного треугольника основание которого равно 13см а боковая сторона 8см.

Решение

Для равнобедренного треугольника, у которого известно основание и боковая сторона нам подходит эта формула.

P=2b+a = 2 cdot 8 + 13 = 16 + 13 = 29 : см

Ответ: 29 см

Проверка .

Задача 5

Найдите периметр равностороннего треугольника, если его высота равна 9см.

Решение

Для равностороннего треугольника с известной высотой мы применим эту формулу.

P = 2sqrt{3}h = 2sqrt{3} cdot 9 = 18sqrt{3} : см approx 31.17691 : см

Ответ: 18sqrt{3} : см approx 31.17691 : см

Проверить ответ поможет калькулятор .

Источник

В данной публикации мы рассмотрим, каким образом можно посчитать периметр треугольника и разберем примеры решения задач.

  • Формула вычисления периметра

  • Примеры задач

Формула вычисления периметра

Периметр (P) любого треугольника равняется сумме длин всех его сторон.

P = a + b + c

Периметр треугольника

Периметр равнобедренного треугольника

Равнобедренным называют треугольник, у которого две боковые стороны равны (примем их за b). Сторона a, имеющая отличную от боковых длину, является основанием. Таким образом, периметр можно считать так:

P = a + 2b

Периметр равностороннего треугольника

Равносторонним или правильным называется треугольник, у которого все стороны равны (примем ее за a). Периметр такой фигуры вычисляется так:

P = 3a

Примеры задач

Задание 1
Найдите периметр треугольника, если его стороны равны: 3, 4 и 5 см.

Решение:
Подставляем в формулу известные по условиям задачи величины и получаем:
P = 3 см + 4 см + 5 см = 12 см.

Задание 2
Найдите периметр равнобедренного треугольника, если его основание равняется 10 см, а боковая сторона- 8 см.

Решение:
Как мы знаем, боковые стороны равнобедренного треугольника равны, следовательно:
P = 10 см + 2 ⋅ 8 см = 26 см.

Источник

Добавить комментарий