Найти периметр параболы y^2 = 2 px и уравнение ее директрисы, если эта парабола проходит через точки пересечения прямой y = x с окружностью x^2 + y^2 — 6x = 0.
Александр
25.12.18
Учеба и наука / Математика
0 ответов
Смачиваемый периметр параболы Калькулятор
| Search | ||
| Дом | Инженерное дело ↺ | |
| Инженерное дело | Гражданская ↺ | |
| Гражданская | Гидравлика и гидротехнические сооружения ↺ | |
| Гидравлика и гидротехнические сооружения | Поток в открытых каналах ↺ | |
| Поток в открытых каналах | Геометрические свойства сечения канала. ↺ | |
| Геометрические свойства сечения канала. | Параболическая секция ↺ |
|
✖Верхняя ширина определяется как ширина в верхней части секции.ⓘ Верхняя ширина [T] |
+10% -10% |
||
|
✖Глубина потока — это расстояние от вершины или поверхности потока до дна канала или другого водного пути или глубина потока по вертикали при измерении звукового веса.ⓘ Глубина потока [df] |
+10% -10% |
|
✖Смоченный периметр параболы определяется как поверхность дна и стенок канала, находящихся в непосредственном контакте с водным телом.ⓘ Смачиваемый периметр параболы [PPara] |
⎘ копия |
Смачиваемый периметр параболы Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Верхняя ширина: 1.33 метр –> 1.33 метр Конверсия не требуется
Глубина потока: 3.3 метр –> 3.3 метр Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
23.1645864661654 метр –> Конверсия не требуется
13 Параболическая секция Калькуляторы
Смачиваемый периметр параболы формула
Смоченный периметр параболы = Верхняя ширина+(8/3)*Глубина потока*Глубина потока/Верхняя ширина
PPara = T+(8/3)*df*df/T
Что такое смачиваемый периметр?
Смачиваемый периметр – это периметр «мокрой» площади поперечного сечения. Длина линии пересечения смачиваемой поверхности канала с плоскостью поперечного сечения, перпендикулярной направлению потока.
Нахождение периметра квадрата
Определение
Квадрат – это такой четырехугольник, который обладает свойствами прямоугольника, параллелограмма, а также ромба:
- Все стороны равны.
- Все углы прямые, то есть по 90°.
- Диагонали равны, а угол их пересечения прямой.
- Диагонали при пересечении делать эти углы пополам.
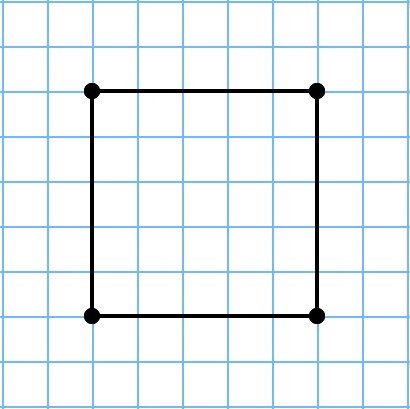
Зная свойства квадрата, можно понять, что его периметр находится путем сложения всех 4 сторон или же умножения его одной стороны на 4. Из этого выведем формулу где a – сторона квадрата:
[P = a + a + a + a]
[P = 4a]
Пример 1
Найдите периметр квадрата, сторона которого равна 6 см.
Решение:
Воспользуемся формулой и подставим числа:
P = a + a + a + a
6 + 6 + 6 + 6 = 24 (см)
Ответ: периметр этого квадрата равен 24 см.
Пример 2
Найдите периметр квадрата, сторона которого равна 10 см.
Решение:
Теперь используем вторую формулу и подставим числа:
P = 4a
4 × 10 = 40 (см)
Ответ: периметр равен 40 см.
Нахождение периметра прямоугольника
Определение
Прямоугольник – это геометрическая фигура, которая может быть квадратом, прямоугольником или же ромбом.
Характеристики:
- У прямоугольника все углы по 90°
- В отличие от квадрата, у прямоугольника равны только противолежащие стороны, которые являются его шириной и высотой. Эти стороны параллельны. Из этого следует, что каждый квадрат – прямоугольник, но квадратом являются не все прямоугольники.
- Его прилегающие стороны перпендикулярны во всех случаях.
- Если провести диагональ, то она поделит прямоугольник на два равных прямоугольных треугольника.
- Если мы имеем две диагонали, то можно утверждать, что они одинаковой длины.
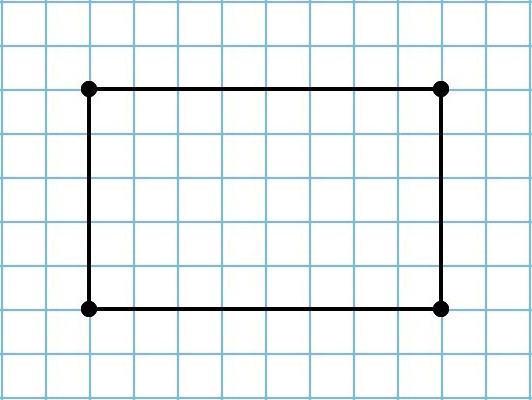
Периметр прямоугольника – это сумма длин всех его сторон. Получается, чтобы найти его периметр, воспользуемся формулами, в которых a – ширина и b – высота:
[P = a + a + b + b]
[P = 2(a + b)]
[P = 2a + 2b]
Пример 1
Найдите периметр прямоугольника, стороны которого равны 8 и 4 см.
Решение:
Воспользуемся формулой и подставим числа:
P = a + a + b + b
8 + 8 + 4 + 4 = 24 (см)
Ответ: периметр этого прямоугольника равен 24 см.
Пример 2
Найдите периметр прямоугольника, стороны которого равны 10 и 12 см.
Решение:
Теперь используем вторую формулу и подставим числа:
P = 2(a + b)
2(10 + 12) = 44 (см)
Ответ: периметр равен 44 см.
Пример 3
Найдите периметр прямоугольника, стороны которого равны 9 и 7.
Решение:
На очереди третья формула. Подставим числа и решим:
P = 2a + 2b
2 × 9 + 2 × 7 = 32 (см)
Ответ: периметр равняется 32 см.
Нахождение периметра параллелограмма
Определение
Параллелограмм – это такой четырехугольник, у которого противоположные стороны парно параллельны.
Характеристики:
- Противоположные стороны равны.
- Противоположные углы равны.
- Диагонали в точке пересечения делятся пополам.
- Как и в прямоугольнике, диагональ параллелограмма делит его на 2 треугольника.
- Два угла на одной стороне равны 180°
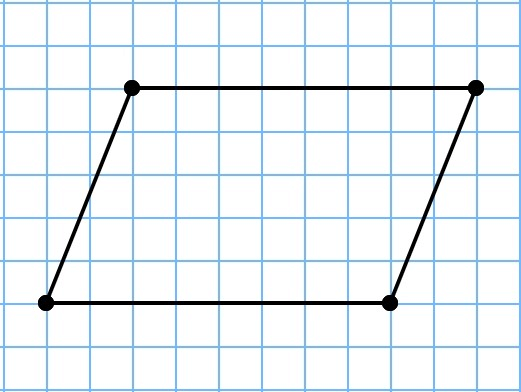
Периметр параллелограмма находится точно так же, как и периметр прямоугольника:
[P = a + a + b + b]
[P = 2(a + b)]
[P = 2a + 2b]
Нахождение периметра трапеции
Формула
Трапеция – это четырехугольник, отличающийся тем, что его две стороны параллельны, а другие две не параллельны.
Характеристики:
- Основа трапеции – это те две параллельные стороны.
- Боковые стороны – не параллельные стороны.
- Если две боковые стороны равны, то можно сделать вывод, что такая трапеция равнобедренная.
- Трапеция с прямыми углами является прямоугольной.
- В трапеции можно провести среднюю линию, которая будет параллельна основаниям, а также равняться их полусумме.
- Если трапеция равнобедренная, то ее углы и длины диагоналей равны.
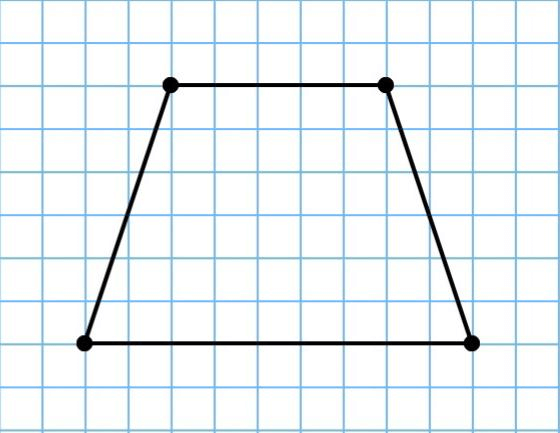
Формула
Чтобы найти периметр трапеции, необходимо знать длины всех ее сторон, чтобы сложить их. Представим, что
стороны трапеции – это a, b, c, d. Получается, для нахождения периметра трапеции, нам надо сложить все ее
стороны:
[P = a + b + c + d]
Пример 1
Найдите периметр трапеции, если известно, что ее стороны равны: 2, 6, 5, 5.
Решение:
Используем формулу:
P = a + b + c + d
2 + 6 + 5 + 5 = 18 (см)
Ответ: периметр трапеции равен 18 см.
Нахождение периметра ромба
Определение
Ромб – это четырехугольник, являющийся параллелограммом с равными сторонами.
Характеристики:
- Стороны и высоты ромба равны.
- Углы диагоналей при пересечении равны 90° — эти углы прямые.
- Диагональ является биссектрисой и делит углы пополам.
- Ромб называется параллелограммом, так как он имеет те же свойства, что и параллелограмм.
- В каждый ромб можно вписать окружность.
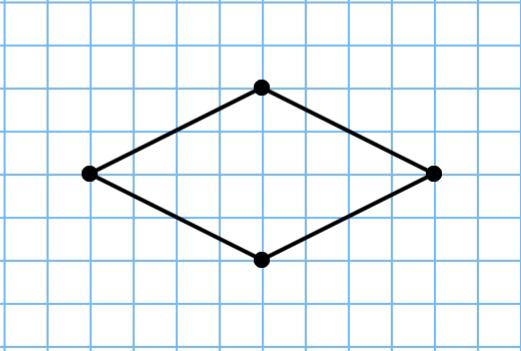
Ромб – это квадрат, а это значит, что найти его периметр можно так, как и периметр квадрата:
[P = a + a + a + a]
[P = 4a]
Нет времени решать самому?
Наши эксперты помогут!
Нахождение периметра многоугольника
Определение
Многоугольник – это геометрическая фигура, которая со всех сторон ограничена ломанной линией.
Характеристики:
- Название многоугольника определяется количеством его вершин. Если у многоугольника количество вершин равно n, то он называется n-угольником.
- Многоугольником являются такие фигуры, как: квадрат, ромб, параллелограмм и т.д.
- Если углы с отрезками равны, то это правильный многоугольник.
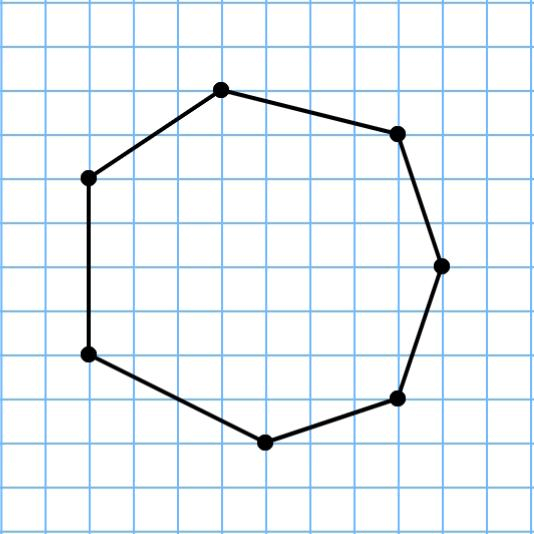
Чтобы найти периметр n-угольника, нужно сложить всего длины его сторон:
[P = a1 + a2 + … an]
А для правильного n-угольника можно выделить еще одну формулу, потому как его стороны равны:
P = na
Здесь мы умножаем длину одной стороны на n.
Пример 1
Найдите периметр правильного многоугольника, если у него 5 вершин, а длина его одной стороны равна 7.
Решение:
Здесь воспользуемся этой формулой:
P = na
7 × 5 = 35 (см)
Ответ: периметр многоугольника равняется 35 см.
Нахождение периметра эллипса
Определение
Эллипс это замкнутая кривая, находящаяся на плоскости. Ее получают с помощью пересечения цилиндра плоскостью.
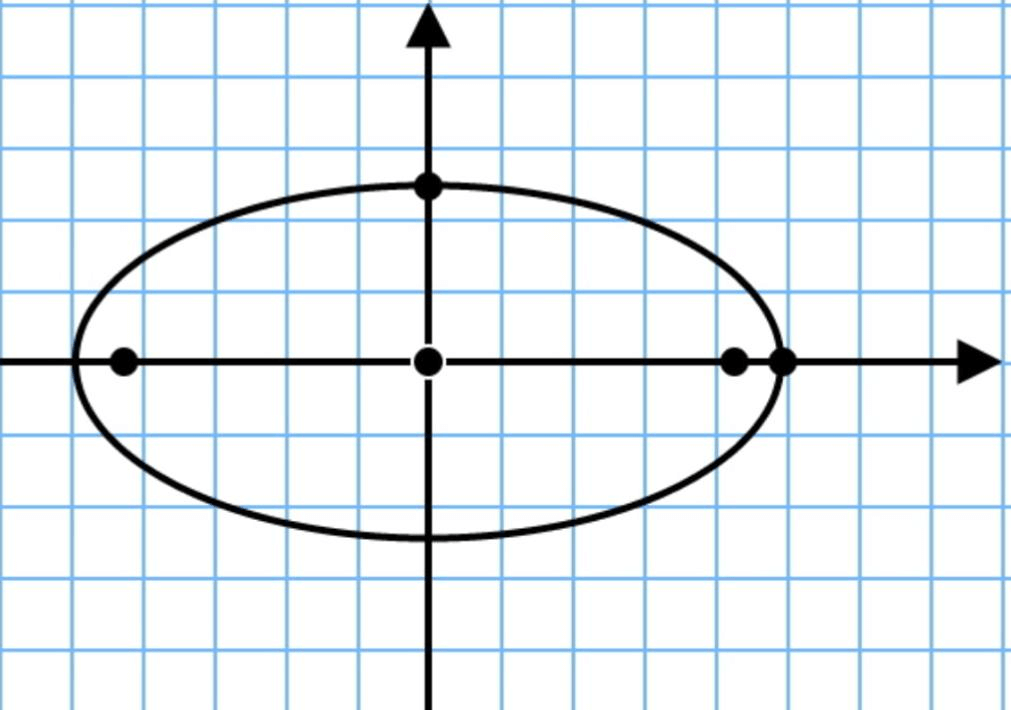
Для нахождения периметра, нужно следовать формуле:
[P=4 pi a b+a-b / a+b]
Калькулятор периметр квадрата
Перейти к содержимому Меню Закрыть
ГДЗ, ответы, контрольные работы, решение заданий, тесты на Знания.ком
Искать:
Знания.ком
Меню
Знания.ком
Искать:
Меню
ГДЗ, ответы, контрольные работы, решение заданий, тесты на Знания.ком
Искать:
Кнопка
- Главная страница
- Вопросы
- как найти периметр параболы?
как найти периметр параболы?
26 просмотров10.07.2022Геометрия
0
admin304.70K 10.07.2022 0 комментариев
как найти периметр параболы?
Регистрация или Вход
Рубрики
- Биология
17385 вопросов
- Русский язык
9844 вопроса
- География
8823 вопроса
- Литература
6037 вопросов
- Геометрия
6030 вопросов
- Технология
6001 вопрос
- Программирование
5367 вопросов
- Обществознание
3011 вопросов
- Музыка
3006 вопросов
- Астрономия
3001 вопрос
Вопросы
Информатика. 9 класс. 3 ответа | 0 Голосов
характеристика автора романа Бедная Лиза 2 ответа | 0 Голосов
Пример со скрытым числом 1 ответ | 0 Голосов
Разработка на Python 1 ответ | 0 Голосов
Обществознание законы 1 ответ | 0 Голосов
Загрузить PDF
Загрузить PDF
Нахождение периметра фигуры – порой непростая задача. Эта статья научит вас находить периметры следующих основных фигур: прямоугольника, квадрата, круга, прямоугольного треугольника, треугольника и правильного многоугольника.
-

1
Найдите длины двух смежных сторон: ширины и высоты. Прямоугольник – фигура с четырьмя сторонами, которые пересекаются под прямым углом, а две противоположные стороны параллельны и равны. Таким образом, две смежные стороны имеют разную длину (ширина и высота; если ширина равна высоте, то такая фигура – квадрат).
- Если даны только одна сторона и площадь прямоугольника, вы можете найти другую сторону по формуле: A=wh, то есть h=A/w или w=A/h. Поэтому, если даны высота и площадь, просто разделите площадь на высоту, чтобы найти ширину. Вы также можете разделить площадь на ширину, чтобы найти высоту.
-

2
Сложите длины двух смежных сторон и умножьте полученное значение на 2. Если w – ширина и h – высота, периметр прямоугольника: P=2(w+h)
Реклама
-

1
Найдите длину стороны квадрата (назовем ее х). Квадрат – фигура, у которой все стороны равны и пресекаются под прямым углом.
-

2
Если дана площадь (A) квадрата, вы можете найти длину стороны, взяв квадратный корень из площади: х = √ (A).
- Если дана диагональ (d) квадрата, Вы можете найти длину стороны, разделив диагональ на квадратный корень из 2: х = d/√2
-

3
Умножьте длину стороны на четыре. Поскольку все четыре стороны имеют одинаковую длину, периметр квадрата равен учетверенной длине одной стороны: Р = 4x.
Реклама
-

1
Найдите длину радиуса (r). Радиус является расстоянием от центра круга до любой точки на окружности.
- Если дан диаметр (d) круга, вы можете найти радиус, разделив диаметр на два: г = d/2
- Если дана площадь (A) круга, вы можете найти радиус, разделив площадь на π, а затем взяв квадратный корень из полученного значения: г = √(A/π)
-

2
Найдите периметр, умножив радиус на 2π: Р = 2πr.
- Так как диаметр – это удвоенный радиус, периметр может быть найден по формуле: P = πd.
Реклама
-

1
Найдите длины двух сторон треугольника (а и b), пересекающихся под прямым углом.
-

2
Найдите сумму квадратов а и b, а затем извлеките квадратный корень из полученной суммы: √(а^2 + b^2). По теореме Пифагора, а^2 + b^2 = с^2, где с – длина гипотенузы, то есть стороны, лежащей напротив прямого угла.
-

3
Теперь, когда у вас есть а, b и с (все три стороны треугольника), просто сложите их для нахождения периметра: P = а+b+с.
Реклама
-

1
Найдите высоту треугольника (у) и его основание (х) (сторона, к которой проведен перпендикуляр – высота).
-

2
Найдите длины отрезков х1 и х2, на которые высота делит основание (то есть х = х1 + х2). Высота делит треугольник на два прямоугольных треугольника (один с катетами х1 и у, другой с катетами х2 и у), и необходимо найти длины гипотенуз этих треугольников с1 и с2.
-

3
Найдите с1 и с2. Для этого используйте теорему Пифагора: а^2 + b^2 = с^2, и подставьте x1 вместо a, y вместо b, c1 вместо c. Повторите для х2, у, и с2.
-

4
Сложите х, с1 и с2, которые являются тремя сторонами исходного треугольника.
Реклама
-

1
Найдите длину одной стороны правильного многоугольника. По определению, правильный многоугольник – это фигура с равными сторонами и углами.
- Если дана апофема (перпендикуляр, опущенный из центра многоугольника к одной из его сторон), Вы можете найти длину стороны. Если n – число сторон многоугольника, А – длина апофемы, длина стороны: x=2Atan(180/n).
- Если дан радиус (расстояние между центром и любой вершиной), вы можете найти длину стороны: x=2rsin(180/n), где r – радиус, n – число сторон многоугольника.
-

2
Умножьте длину одной стороны многоугольника на число его сторон. Таким образом, P=nx, где n – число сторон многоугольника, х – длина одной стороны многоугольника.
Реклама
Об этой статье
Эту страницу просматривали 16 024 раза.

