meryinga531
Вопрос по геометрии:
Биссектриса параллелограмма делит противолежащую сторону на части 13 см и 6 см. Найти периметр параллелограмма.
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!
Ответы и объяснения 1
maikbent55
Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник (свойство).
Пусть биссектриса делит сторону ВС на отрезки ВР и РС.
Следовательно, в параллелограмме АВ=CD=ВР, BC=AD=ВР+РС=19см.
Если ВР=13см, а РС=6см, то АВ=13см и
тогда периметр параллелограмма равен Р=2(АВ+ВС)= 2*(13+19)=64см.
Если ВР=6см, а РС=13см, то АВ=6см и
тогда периметр равен Р=2(АВ+ВС)=2(6+19)=50см.

Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат – это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,655 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,944 -
разное
16,904
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
ГДЗ и решебники
вип уровня
- ГДЗ
- 7 класс
- Геометрия
- Атанасян
- Задание 375

Условие
Найдите периметр параллелограмма, если биссектриса одного из его углов делит сторону параллелограмма на отрезки 7 см и 14 см.
Решение 1

Решение 2

Решение 3
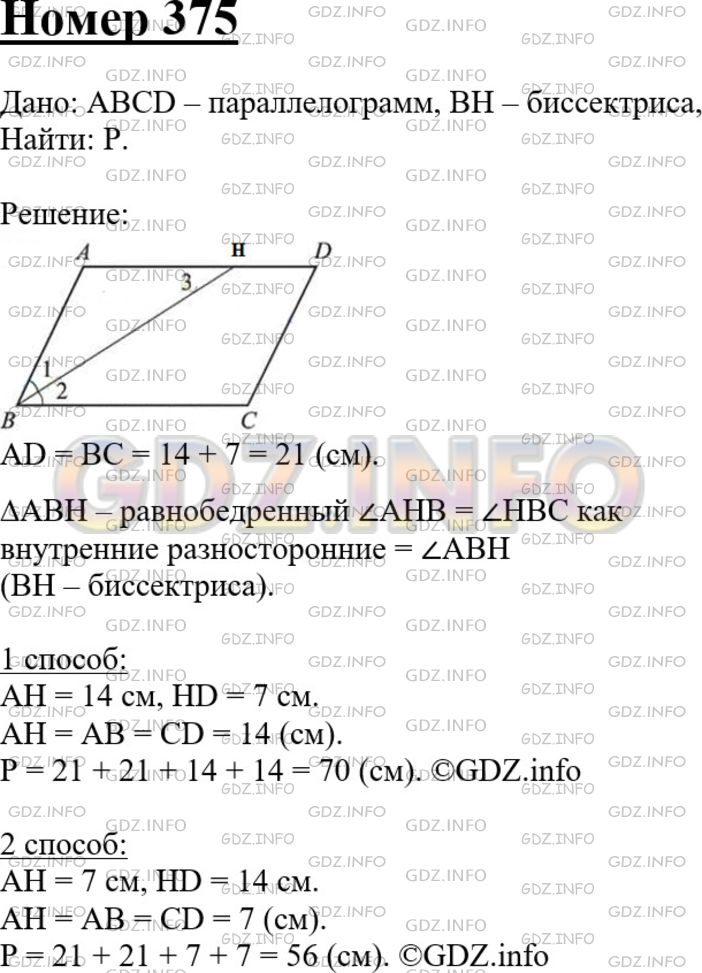
Решение 4

Популярные решебники
Выпускники, которые рассчитывают успешно сдать ЕГЭ, в обязательном порядке должны повторить тему «Свойства биссектрисы параллелограмма». Как показывает статистика, при прохождении аттестационного испытания задачи по данному разделу планиметрии вызывают сложности у большого количества учащихся. При этом задания, в которых необходимо применить свойства биссектрисы угла параллелограмма, встречаются в ЕГЭ ежегодно. Таким образом, справляться с ними должны все учащиеся.
Образовательный портал «Школково» предлагает выстроить процесс подготовки к прохождению аттестационного испытания по-новому. Занимаясь вместе с нашим ресурсом, выпускники смогут определить наиболее сложные для себя темы и ликвидировать пробелы в знаниях.
Чтобы задания ЕГЭ не вызывали трудностей, рекомендуем вначале повторить основные понятия и свойства биссектрисы параллелограмма. Найти этот материал учащиеся смогут в разделе «Теоретическая справка».
Для того чтобы окончательно понять принцип решения задач по данному разделу планиметрии, мы рекомендуем выполнить соответствующие упражнения. Большая подборка заданий различного уровня сложности представлена в разделе «Каталог». Для каждого упражнения на сайте приведен алгоритм решения и дан правильный ответ. Последовательно выполняя их, учащиеся смогут понять, как правильно применять свойства биссектрисы внутреннего угла параллелограмма.
Получать новые знания и оттачивать собственные навыки по данной теме или, например, в решении задач на тему «Прямоугольник» в ЕГЭ учащиеся могут в онлайн-режиме, находясь в Москве или любом другом российском городе. При необходимости задание можно сохранить в разделе «Избранное». Благодаря этому вы сможете быстро найти интересующие примеры и обсудить алгоритмы нахождения правильного ответа с преподавателем.

