Можно, конечно, рисовать рисунок. Можно чертить чертёж. Только почему-то мне видится, что сам параллелограмм при этом должен иметь несколько другие пропорции. Ведь отрезок CK, не меньше, а существенно больше отрезка BK (14/9=1,555555555555 и 5 в периоде). Тогда выглядеть он может следующим образом:
Можете по клеточкам проверить – всё сходится. Но задача в другом – нам нужно найти периметр геометрической фигуры ABCD. И для этого я предлагаю провести ещё один отрезок из точки K, который будет параллелен сторонам AB и CD. Пусть это будет отрезок KL:
Но в таком случае мы явно получаем ромб ABKL, потому что у ромба диагонали являются биссектрисами его углов. А в условии задачи как раз об одной такой биссектрисе и говорится – она делит пополам угол ∠BAD. И, если это ромб, то все его стороны будут равны 9-ти. А периметр ромба равен сумме этих четырёх девяток.
- P(р) = 4 * 9 = 36.
А чем же периметр параллелограмма отличается от периметра найденного ромба? Две стороны одинаковые. А две другие больше на 14. Тогда и периметр параллелограмма будет больше на две эти разницы.
- P(п) = P(р) + 2 * 14 = P(р) + 28 = 36 + 28 = 64.
По-моему, всё логично.
ГДЗ и решебники
вип уровня
- ГДЗ
- 7 класс
- Геометрия
- Атанасян
- Задание 375
Условие
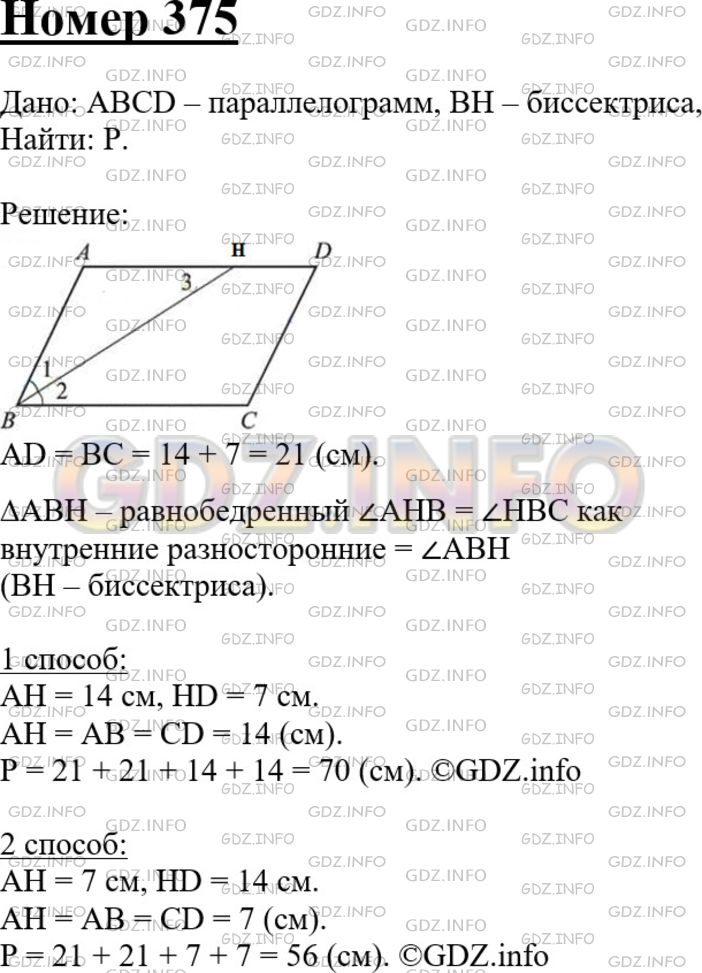
Найдите периметр параллелограмма, если биссектриса одного из его углов делит сторону параллелограмма на отрезки 7 см и 14 см.
Решение 1
Решение 2
Решение 3
Решение 4
Популярные решебники
Задания
Версия для печати и копирования в MS Word
Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK = 7, CK = 12.
Спрятать решение
Решение.
Углы BKA и KAD равны как накрест лежащие углы при параллельных прямых, поэтому углы BAK и BKA также равны. Следовательно, треугольник ABK — равнобедренный, откуда AB = BK = 7. Противоположные стороны параллелограмма равны. Периметр параллелограмма равен сумме длин всех его сторон P = 2(BC + AB) = 2(7 + 12 + 7) = 52.
Ответ: 52.
Выпускники, которые рассчитывают успешно сдать ЕГЭ, в обязательном порядке должны повторить тему «Свойства биссектрисы параллелограмма». Как показывает статистика, при прохождении аттестационного испытания задачи по данному разделу планиметрии вызывают сложности у большого количества учащихся. При этом задания, в которых необходимо применить свойства биссектрисы угла параллелограмма, встречаются в ЕГЭ ежегодно. Таким образом, справляться с ними должны все учащиеся.
Образовательный портал «Школково» предлагает выстроить процесс подготовки к прохождению аттестационного испытания по-новому. Занимаясь вместе с нашим ресурсом, выпускники смогут определить наиболее сложные для себя темы и ликвидировать пробелы в знаниях.
Чтобы задания ЕГЭ не вызывали трудностей, рекомендуем вначале повторить основные понятия и свойства биссектрисы параллелограмма. Найти этот материал учащиеся смогут в разделе «Теоретическая справка».
Для того чтобы окончательно понять принцип решения задач по данному разделу планиметрии, мы рекомендуем выполнить соответствующие упражнения. Большая подборка заданий различного уровня сложности представлена в разделе «Каталог». Для каждого упражнения на сайте приведен алгоритм решения и дан правильный ответ. Последовательно выполняя их, учащиеся смогут понять, как правильно применять свойства биссектрисы внутреннего угла параллелограмма.
Получать новые знания и оттачивать собственные навыки по данной теме или, например, в решении задач на тему «Прямоугольник» в ЕГЭ учащиеся могут в онлайн-режиме, находясь в Москве или любом другом российском городе. При необходимости задание можно сохранить в разделе «Избранное». Благодаря этому вы сможете быстро найти интересующие примеры и обсудить алгоритмы нахождения правильного ответа с преподавателем.
В прошлый раз мы рассмотрели свойства параллелограмма, в котором точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит его противоположной стороне. Перейдем к примерам использования этих свойств.
Задача 1.
Биссектрисы углов параллелограмма пересекаются в точке, принадлежащей противоположной стороне. Найти периметр параллелограмма, если его большая сторона равна 40 см.

AF — биссектриса ∠BAD,
DF — биссектриса ∠ADC, F∈BC, BC=20 см.
Найти:
Решение:
Если биссектрисы двух углов параллелограмма, прилежащих к одной стороне, пересекаются в точке, принадлежащей противоположной стороне, то одна сторона параллелограмма в два раза больше другой. Значит,
Периметр параллелограмма ABCD равен
Ответ: 120 см.
Задача 2.
Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, F, принадлежащей стороне BC. ∠D=120º, DF=8. Найти периметр ABCD и AF.

AF — биссектриса ∠BAD,
DF — биссектриса ∠ADC, F∈BC,
∠D=120º, DF=8.
Найти:
Решение:

Так как биссектрисы углов параллелограмма, прилежащих к одной стороне, взаимно перпендикулярны, то ∠AFD=90º.
Так как FD- биссектриса угла ADC, то
Так как биссектриса параллелограмма отсекает от него равнобедренный треугольник, треугольник CDF — равнобедренный с основанием DF. А так как ∠CDF=60º, то треугольник CDF — равносторонний, и CD=DF=8.
Так как биссектрисы углов A и D параллелограмма пересекаются в точке, принадлежащей противоположной стороне, то одна сторона параллелограмма в два раза больше другой: BC=2AB.
Ответ: 48; 8√3.