Как найти периметр параллелограмма если известны высоты и площадь?
Vlada Mudrenco
Знаток
(336),
закрыт
5 лет назад
Nikita Russian
Гуру
(2818)
5 лет назад
Ну дай условие самой задачи, я может быть попытаюсь решить.
Vlada MudrencoЗнаток (336)
5 лет назад
Высоты параллелограмма равны 8 см и 6 см, а его площадь 72 см^2 . Найдите периметр параллелограмма
Nikita Russian
Гуру
(2818)
Да ххххуй его знает… Я даже не знал, что у параллелограмма высоты разной величины.
В этой задаче удобней смотреть на рисунок для понимания

1) Точка пересечения удалена от сторон на расстояние – это означает что опущены перпендикуляры из этой точки на стороны и длинны этих перпендикуляров равны 2 см и 3 см
Перпендикуляры опущенные на параллельные стороны из одной точки будут лежать на одной прямой. (Если вдруг они не лежат на одной прямой, то тогда получится, что к одной прямой из точки опущено 2 перпендикуляра, что невозможно)
2) Так как точкой пересечения диагонали делятся пополам и вертикальные углы при пересечении двух прямых (диагоналей) равны, то пересечением диагоналей и сторонами параллелограмма будут образованы две пары равных треугольников напротив друг друга. А в равных треугольниках равны соответсвующие элементы, поэтому расстояния от точки пересечения (вершины треугольников) до равных сторон будут одинаковыми.
Таким образом 2+2 = 4 см и 3+3 = 6 см будут расстояниями между параллельными сторонами – а это есть высоты параллелограмма.
3) Площадь параллелограмма равна: сторона умножить на высоту параллелограмма к этой стороне: S = a•4 и S = b•6
Откуда: a = 24/4 = 6 см; b = 24/6 = 4 см
Периметр: P = 2•(a+b) = 2•(6+4) = 20 см
Ответ: P = 20 см
Что такое периметр параллелограмма
Периметр параллелограмма — это сумма длин всех его сторон.
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно равны и параллельны друг другу. Таким образом, его периметр — это удвоенная сумма двух его смежных ребер.
Свойства
- противоположные стороны равны и параллельны;
- противоположные углы попарно равны;
- сумма соседних углов равна 180 градусов;
- сумма всех углов равна 360 градусов;
- диагонали фигуры делятся пополам в точке пересечения;
- точка пересечения диагоналей — центр симметрии параллелограмма;
- биссектриса образует равнобедренный треугольник.
Как найти периметр
Существует несколько основных способов, с помощью которых можно найти сумму длин всех сторон заданной фигуры. Все они зависят от изначально известных параметров.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
По сумме всех сторон
Так как периметр параллелограмма — это удвоенная сумма двух его смежных ребер, используем формулу:
P=2(a+b),
где a и b — это две смежные стороны данного четырехугольника.
По стороне и двум диагоналям
Если в задаче дана лишь одна сторона, но обе диагонали четырехугольника, мы можем найти вторую сторону. Для этого используем формулу:
(a=frac{sqrt{2d_1^2+2d_2^2-4b^2}}2,)
где (d_1) и (d_2) — это обе диагонали фигуры.
Получается, что расчет суммы длин всех сторон для параллелограмма будет выглядеть так:
(P=2(frac{sqrt{2d_1^2+2d_2^2-4b^2}}2+b).)
По стороне, высоте и синусу угла
В случае, если нам известны лишь одно ребро, высота и один из углов, можем узнать длину второго ребра таким образом:
(a=frac{h_b}{sinalpha})
где (h_b) — высота, проведенная к известной стороне, а (sinalpha) — известный нам угол.
Таким образом, формула для нахождения периметра параллелограмма будет выглядеть так:
(P=2(frac{h_b}{sinalpha}+b))
Примеры решения задач
Попробуем применить полученные знания на практике и рассмотрим несколько задач на периметр параллелограмма.
Задача 1
Дан параллелограмм со сторонами 5 см и 9 см. Вычислить его периметр.
Решение:
Воспользуемся формулой P=2(a+b), так как нам известны обе стороны фигуры. Подставляем значения: P=2(5+9)=28 см.
Ответ: 28 см.
Задача 2
Известно, что одна из сторон параллелограмма равна 4 см, а две его диагонали равны 6 см и 8 см. Найти периметр фигуры.
Решение:
Для расчета суммы длин всех сторон используем формулу:
(P=2(frac{sqrt{2d_1^2+2d_2^2-4b^2}}2+b))
Подставляем известные значения:
(P=2(frac{sqrt{2d_1^2+2d_2^2-4b^2}}2+b)=2(frac{sqrt{2times6^2+2times8^2-4times4^2}}2+4)=2(frac{sqrt{72+128-64}}2+4)=2(frac{2sqrt{34}}2+4)=2sqrt{34}+8) см.
Ответ:( 2sqrt{34}+8) см.
Задача 3
Сторона b параллелограмма равна 2 см, высота, проведенная к b — 1 см, а угол α равен (fracpi6). Найти сумму длин всех сторон фигуры.
Решение:
Для расчета будем использовать уравнение:
(P=2(frac{h_b}{sinalpha}+b))
Подставим известные величины:
(P=2(frac1{sin{displaystylefracpi6}}+2)=2(frac1{displaystylefrac12}+2)=8;)см.
Ответ: 8 см.
В данной публикации мы рассмотрим, каким образом можно посчитать периметр параллелограмма и разберем примеры решения задач.
- Формула вычисления периметра
- Примеры задач
Формула вычисления периметра
Периметр (P) параллелограмма равняется сумме длин всех его сторон. А т.к. противоположные стороны данной фигуры равны, формулу можно представить в следующем виде:
P = 2 * (a + b) или P = 2a + 2b

Примеры задач
Задание 1
Найдите периметр параллелограмма, если его стороны равны 6 и 8 см.
Решение:
Воспользуемся одной из двух формул выше, подставив в нее известные значения: P = 2 * 6 см + 2 * 8 см = 28 см.
Тот же самый результат получится, если применить вторую формулу: P = 2 * (6 см + 8 см) = 28 см.
Задание 2
Периметр параллелограмма равен 50 см. Найдите его вторую сторону, если известно, что первая равна 7 см.
Решение:
Нам известно, что периметр считается по формуле: P = 2a + 2b.
Допустим a – это известная сторона, и нам нужно найти b. Ее длина, умноженная на два, равна: 2b = P – 2a = 50 см – 2 * 7 см = 36 см.
Следовательно, длина неизвестной стороны составляет: b = 36 см / 2 = 18 см.

Как найти периметр параллелограмма
В школьной программе, по геометрии, можно часто встретить задания, в которых необходимо найти периметр параллелограмма. Для его нахождения нужно использовать всего лишь одну простую формулу.
1
Что такое параллелограмм?
- Параллелограмм – в переводе с греческого означает параллельный.
- По своей структуре параллелограмм – это четырехугольник, стороны которого параллельны друг другу. Две его боковые стороны ложатся наискось. Каждая из сторон равна друг другу, т. е, равны противоположные углы. Но каждая из прилегающих сторон может отличаться размером.
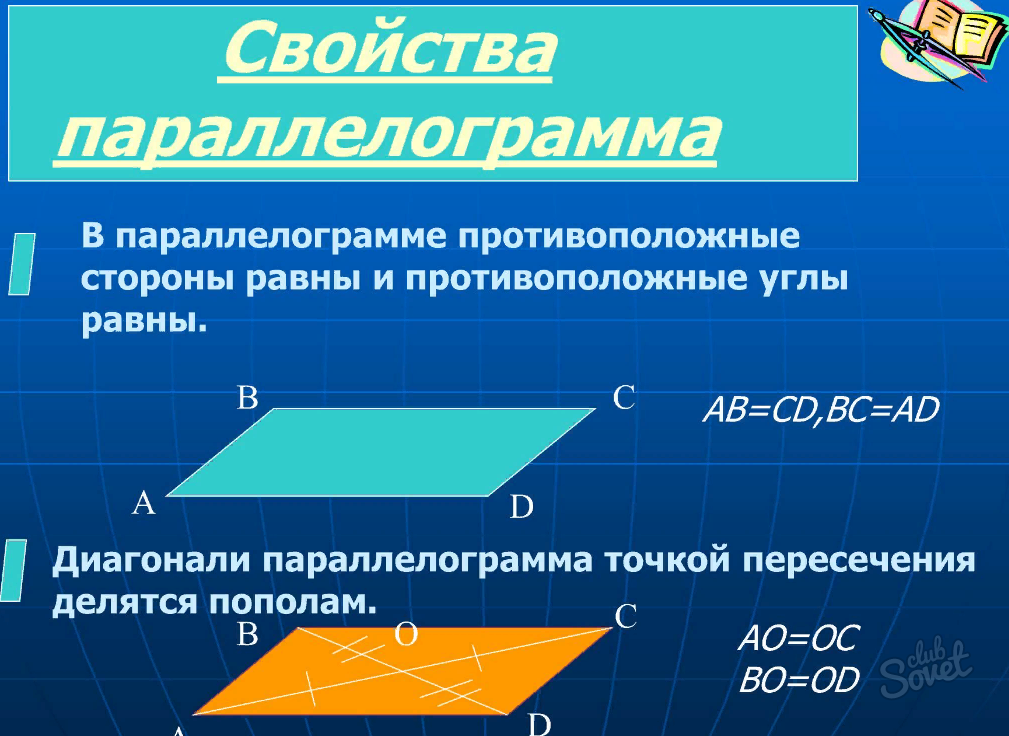
- В основном четырехугольник обозначается большими заглавными буквами ABCD.
- Еще одной особенностью параллелограмма, является тот факт, что он может являться квадратом, прямоугольником или ромбом.
- Чтобы вычислить является ли четырехугольник параллелограммом, необходимо использовать правила нахождения параллелограмма. Одним из таких правил является тот факт, когда его диагонали пересекаются и точкой пересечения делятся пополам.
- Считается, что общая сумма углов, которые лежат параллельно, должна равняться 180 °С, т.е. A + B + C + D = 180 °С. Чтобы вычислить, нужно использовать правило параллельных прямых.

2
Что такое площадь параллелограмма?
- Площадью параллелограмма называется геометрическая фигура, у которой есть основание, высота, а также боковые стороны равны между собой.
- Для того, чтобы приступить к вычислению площади параллелограмма необходимо знать его высоту, а также измерить боковые стороны.
- Существуют специальные теоремы и доказательства, при помощи которых легко вычислить площадь параллелограмма.

3
Как найти периметр параллелограмма?
- Чтобы найти общую численную характеристику параллелограмма необходимо использовать формулу. Такая формула может изменяться, зависимости от заданных значений.
- Чтобы найти периметр необходимо воспользоваться основной формулой: P = 2 * (a + b), где а – верхняя сторона, b – боковая сторона.
- Например, одна из боковых сторон параллелограмма – а равна 4 см, а сторона b, которая перпендикулярно ей – 6 см. Вычисли периметр, используя формулу: a = 6 см, b = 4 см. P = 2 * (6+4) = 10 * 2 = 20 см.
- Значит, периметр данного параллелограмма будет равен 20 см.
- Значение периметра может измеряться при помощи единицы измерения длины.
- Периметр параллелограмма всегда равен удвоенной сумме двух его сторон.
Кроме периметра, также при помощи формул можно найти любое значение данной геометрической фигуры: высоту, площадь, площадь по вписанной окружности и другие необходимые параметры.
