Как найти периметр параллелограмма формула с биссектрисой

Параллелограмм это геометрическая фигура имеющая четыре параллельные стороны, противоположных друг другу. В школьной программе все задания по решению параллелограмма, направлены на нахождение высоты, площади, диагонали и периметра. О них и пойдет речь.

Параллелограмм обладает свойствами, такими как:
В параллелограмме и углы и стороны, которые противоположны между собой одинаковы: АВ = CD, BC =AD. Так же как углы АВС = ADC и ВАD = BCD.
Диагонали проведенные из углов параллелограмма в месте пересечения разделятся на две одинаковые части. АО = ОС, ОВ = OD.
Сумма двух углов, одной стороны всегда 180 градусов.
углы: А + В = 1800, В + С = 1800, С + D =1800, A + D = 1800 .
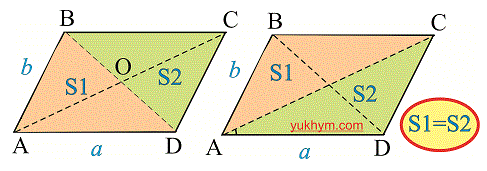
Любая диагональ разделяет параллелограмм на две одинаковые фигуры (треугольник) как по площади так и по размеру.

Зачастую встречается такое интересное свойство как, сума диагоналей в квадрате одинакова с суммой сторон в квадрате.
АС2 + BD2 = (AB2 + BC2). AC2 + BD2 = 2 * (AB2 + BC2)

У параллелограмма есть несколько основных признаков.

– Четырехугольная фигура с противоположными сторонами параллельными друг другу и есть параллелограмм.

– Четырехугольная фигура имеющая одинаковые противоположные стороны, есть параллелограмм.
– Четырехугольная фигура имеющая одинаковые параллельные и противоположные стороны, есть параллелограмм.
– Когда встречающиеся диагонали четырехугольной фигуры в месте пересечения разделяются на равные части. Данная фигура является параллелограммом.
– Четырехугольная фигура в которой противоположные углы одинаковы называется параллелограммом.

Периметр параллелограмма находится по формуле

Р = 2 (а+b)

что означает что периметр равняется двойной сумме сторон.

Биссектриса параллелограмма

Из школьной программы помню определение которое засело в памяти на всю жизнь – Биссектриса это крыса, что ходит по углам и делит угол пополам. Если же говорить научным языком, то:
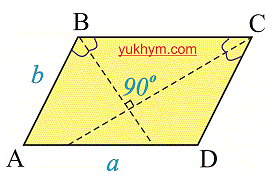
Биссектрисы углов находящихся на одной стороне встречаются в точке пересечения под углом в 90 градусов.

Так же они могут совпадать и быть параллельны друг другу.

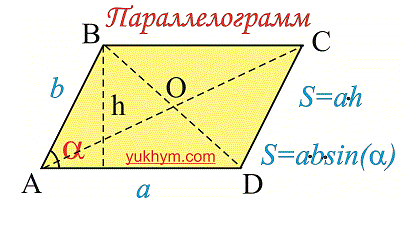
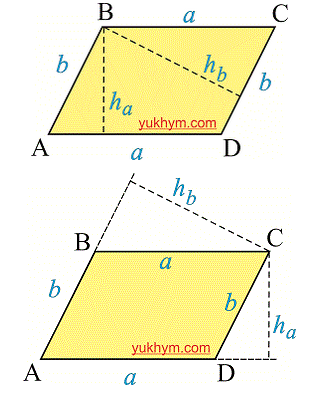
Так же в параллелограмме можно найти высоту, она обозначается в виде отрезка исходящего из угла к основанию, следовательно, от каждого угла их можно провести две.

Площадь параллелограмма это произведение стороны и высоты приведенную к ней. Находится по формуле.

S = a * ha = b * hb

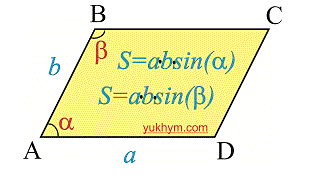
Есть еще один способ вычисления, но им не так часто пользуются в расчетах. Она звучит как площадь параллелограмма это произведение рядом лежащих сторон умноженный на синус угла находящегося между ними.

S = a * b * sin(?) = a * b * sin(?)

Все приведенные в данной статье формулы помогут Вам в решении различных задач по нахождению величин параллелограмма, это не сложно но очень интересно.

Заметка: если Вы находитесь в поиске персонала. Империя кадров поможет вам в этом вопросе. Просто перейдите по ссылке персонал временный (http://www.imperia.ru/client/temp_staff/) и узнайте подробнее.

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

Что такое периметр параллелограмма

Периметр параллелограмма — это сумма длин всех его сторон.

Параллелограмм — это четырехугольник, у которого противоположные стороны попарно равны и параллельны друг другу. Таким образом, его периметр — это удвоенная сумма двух его смежных ребер.

Свойства

• противоположные стороны равны и параллельны;
• противоположные углы попарно равны;
• сумма соседних углов равна 180 градусов;
• сумма всех углов равна 360 градусов;
• диагонали фигуры делятся пополам в точке пересечения;
• точка пересечения диагоналей — центр симметрии параллелограмма;

• биссектриса образует равнобедренный треугольник.

Как найти периметр

Существует несколько основных способов, с помощью которых можно найти сумму длин всех сторон заданной фигуры. Все они зависят от изначально известных параметров.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

По сумме всех сторон

Так как периметр параллелограмма — это удвоенная сумма двух его смежных ребер, используем  формулу:

P=2(a+b),

где a и b — это две смежные стороны данного четырехугольника.

По стороне и двум диагоналям

Если в задаче дана лишь одна сторона, но обе диагонали четырехугольника, мы можем найти вторую сторону. Для этого используем формулу:

(a=frac{sqrt{2d_1^2+2d_2^2-4b^2}}2,)

где (d_1) и (d_2) — это обе диагонали фигуры.

Получается, что расчет суммы длин всех сторон для параллелограмма будет выглядеть так:

(P=2(frac{sqrt{2d_1^2+2d_2^2-4b^2}}2+b).)

По стороне, высоте и синусу угла

В случае, если нам известны лишь одно ребро, высота и один из углов, можем узнать длину второго ребра таким образом:

(a=frac{h_b}{sinalpha})

где (h_b) — высота, проведенная к известной стороне, а (sinalpha) — известный нам угол.

Таким образом, формула для нахождения периметра параллелограмма будет выглядеть так:

(P=2(frac{h_b}{sinalpha}+b))

Примеры решения задач

Попробуем применить полученные знания на практике и рассмотрим несколько задач на периметр параллелограмма.

Задача 1

Дан параллелограмм со сторонами 5 см и 9 см. Вычислить его периметр.

Решение:

Воспользуемся формулой P=2(a+b), так как нам известны обе стороны фигуры. Подставляем значения: P=2(5+9)=28 см.

Ответ: 28 см.

Задача 2

Известно, что одна из сторон параллелограмма равна 4 см, а две его диагонали равны 6 см и 8 см. Найти периметр фигуры.

Решение:

Для расчета суммы длин всех сторон используем формулу:

(P=2(frac{sqrt{2d_1^2+2d_2^2-4b^2}}2+b))

Подставляем известные значения:

(P=2(frac{sqrt{2d_1^2+2d_2^2-4b^2}}2+b)=2(frac{sqrt{2times6^2+2times8^2-4times4^2}}2+4)=2(frac{sqrt{72+128-64}}2+4)=2(frac{2sqrt{34}}2+4)=2sqrt{34}+8) см.

Ответ:( 2sqrt{34}+8) см.

Задача 3

Сторона b параллелограмма равна 2 см, высота, проведенная к b — 1 см, а угол α равен (fracpi6). Найти сумму длин всех сторон фигуры.

Решение:

Для расчета будем использовать уравнение:

(P=2(frac{h_b}{sinalpha}+b))

Подставим известные величины:

(P=2(frac1{sin{displaystylefracpi6}}+2)=2(frac1{displaystylefrac12}+2)=8;)см.

Ответ: 8 см.

Выпускники, которые рассчитывают успешно сдать ЕГЭ, в обязательном порядке должны повторить тему «Свойства биссектрисы параллелограмма». Как показывает статистика, при прохождении аттестационного испытания задачи по данному разделу планиметрии вызывают сложности у большого количества учащихся. При этом задания, в которых необходимо применить свойства биссектрисы угла параллелограмма, встречаются в ЕГЭ ежегодно. Таким образом, справляться с ними должны все учащиеся.

Образовательный портал «Школково» предлагает выстроить процесс подготовки к прохождению аттестационного испытания по-новому. Занимаясь вместе с нашим ресурсом, выпускники смогут определить наиболее сложные для себя темы и ликвидировать пробелы в знаниях.

Чтобы задания ЕГЭ не вызывали трудностей, рекомендуем вначале повторить основные понятия и свойства биссектрисы параллелограмма. Найти этот материал учащиеся смогут в разделе «Теоретическая справка».

Для того чтобы окончательно понять принцип решения задач по данному разделу планиметрии, мы рекомендуем выполнить соответствующие упражнения. Большая подборка заданий различного уровня сложности представлена в разделе «Каталог». Для каждого упражнения на сайте приведен алгоритм решения и дан правильный ответ. Последовательно выполняя их, учащиеся смогут понять, как правильно применять свойства биссектрисы внутреннего угла параллелограмма.

Получать новые знания и оттачивать собственные навыки по данной теме или, например, в решении задач на тему «Прямоугольник» в ЕГЭ учащиеся могут в онлайн-режиме, находясь в Москве или любом другом российском городе. При необходимости задание можно сохранить в разделе «Избранное». Благодаря этому вы сможете быстро найти интересующие примеры и обсудить алгоритмы нахождения правильного ответа с преподавателем.

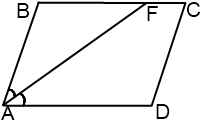
Рассмотрим одну из базовых задач планиметрии — биссектриса угла параллелограмма делит противолежащую сторону на отрезки.

Утверждение.

Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.

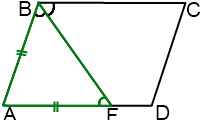
Пусть биссектриса угла A параллелограмма ABCD делит противолежащую сторону на отрезки BF=m, FC=n. Тогда:

1)∠BAF=∠FAD

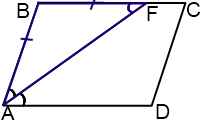
(так как AF — биссектриса угла A по условию);

2) ∠BFA=∠FAD (как внутренние накрест лежащие при AD ∥ BC и секущей AF);

3) следовательно, ∠BAF=∠BFA;

4) следовательно, треугольник ABF — равнобедренный (по признаку);

5) следовательно, AB=BF=m.

Этот рисунок иллюстрирует случай, когда дана биссектриса острого угла параллелограмма.

Если в задаче сказано, что биссектриса тупого угла параллелограмма делит сторону на отрезки, рассуждения аналогичны.

На базе этой задачи существует много других задач. Например: биссектриса угла A параллелограмма ABCD делит противолежащую сторону BC на отрезки BF=m, FC=n. Найти периметр параллелограмма.

После доказательства того, что AB=BF=m, нахождение периметра не вызывает затруднений: P=2(AB+BC)=2(m+m+n).

В прошлый раз мы рассмотрели свойства параллелограмма, в котором точка пе­ре­се­че­ния бис­сек­трис двух углов па­рал­ле­ло­грам­ма, при­ле­жа­щих к одной сто­ро­не, при­над­ле­жит его про­ти­во­по­лож­ной сто­ро­не. Перейдем к примерам использования этих свойств.

Задача 1.

Биссектрисы углов параллелограмма пересекаются в точке, принадлежащей про­ти­во­по­лож­ной сто­ро­не. Найти периметр параллелограмма, если его большая сторона равна 40 см.

Дано: ABCD — параллелограмм,

AF — биссектриса ∠BAD,

DF — биссектриса ∠ADC, F∈BC, BC=20 см.

Найти:

Решение:

Если биссектрисы двух углов параллелограмма, прилежащих к одной стороне, пересекаются в точке, принадлежащей противоположной стороне, то одна сторона параллелограмма в два раза больше другой. Значит,

Периметр параллелограмма ABCD равен

Ответ: 120 см.

Задача 2.

Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, F, принадлежащей  сто­ро­не BC. ∠D=120º, DF=8. Найти периметр ABCD и AF.

Дано: ABCD — параллелограмм,

AF — биссектриса ∠BAD,

DF — биссектриса ∠ADC, F∈BC,

∠D=120º, DF=8.

Найти:

Решение:

Рассмотрим треугольник AFD.

Так как биссектрисы углов параллелограмма, прилежащих к одной стороне, взаимно перпендикулярны, то ∠AFD=90º.

Так как FD- биссектриса угла ADC, то

Так как биссектриса параллелограмма отсекает от него равнобедренный треугольник, треугольник CDF — равнобедренный с основанием DF. А так как ∠CDF=60º, то треугольник CDF — равносторонний, и CD=DF=8.

Так как биссектрисы углов A и D параллелограмма пересекаются в точке, принадлежащей противоположной стороне, то одна сторона параллелограмма в два раза больше другой: BC=2AB.

Ответ: 48; 8√3.