Зная периметр основания правильной пирамиды, можно легко вычислить сторону основания, разделив периметр на удвоенное количество сторон многоугольника. Площадь основания в свою очередь будет рассчитываться по стандартной формуле площади правильного многоугольника, в которую необходимо будет подставить выражение, соответствующее стороне основания через периметр.
a=P/n
S=(na^2)/(4 tan〖(180°)/n〗 )=P^2/(4n tan〖(180°)/n〗 )
Чтобы найти радиус окружности, вписанной в правильный многоугольник в основании пирамиды, как и радиус окружности, описанной вокруг основания, необходимо знать сторону основания, поэтому здесь также пригодится полученное через периметр выражение. (рис.34.1,34.2)
r=a/(2 tan〖(180°)/n〗 )=P/(2n tan〖(180°)/n〗 )
R=a/(2 sin〖(180°)/n〗 )=P/(2n sin〖(180°)/n〗 )
Величина внутреннего угла многоугольника в основании зависит только от количества сторон многоугольника и рассчитывается по следующей формуле. (рис.34.3)
γ=180°(n-2)/n
Зная апофему и сторону основания правильной пирамиды, вычисленной через периметр, можно рассчитать боковое ребро и высоту пирамиды по теореме Пифагора в прямоугольных треугольниках. (рис. 34.4, 35.1)
h=√(l^2-r^2 )=√(l^2-(P/(2n tan〖(180°)/n〗 ))^2 )
b=√(l^2+P^2/(4n^2 ))
Чтобы найти угол между основанием и апофемой, а также между основанием и боковым ребром, нужно сначала рассчитать косинусы этих углов в прямоугольных треугольниках, образованных высотой и соответствующим отрезком, которые через основание будут соединяться радиусы вписанной и описанной окружностей. (рис.34.4, 34.5)
cosα=R/b=P/(2n sin〖(180°)/n〗 √(l^2+P^2/(4n^2 )))
cosβ=r/l=P/(2nl tan〖(180°)/n〗 )
Площадь боковой поверхности правильной пирамиды через периметр основания равна произведению периметра на половину апофемы. Площадь полной поверхности вычисляется как сумма полученного значения и площади основания.
S_(б.п.)=lP/2
S_(п.п.)=P(l/2+P/(2n tan〖(180°)/n〗 ))
Чтобы найти объем пирамиды, необходимо знать не только периметр основания для расчета его площади, но и высоту пирамиды, которая равна квадратному корню из разности квадратов апофемы и радиуса вписанной в основание окружности.
V=1/3 S_(осн.) h=(P^2 √(l^2-(P/(2n tan〖(180°)/n〗 ))^2 ))/(12n tan〖(180°)/n〗 )
Сфера, которую можно вписать в пирамиду, должна иметь радиус, равный отношению трех объемов к площади полной поверхности, которые можно вычислить через периметр и апофему пирамиды. Радиус сферы, которую можно описать вокруг пирамиды, должен быть равен квадрату боковой стороны, деленному на удвоенную высоту. (рис.34.6, 34.7)
r_1=3V/S_(п.п.) =(P√(l^2-(P/(2n tan〖(180°)/n〗 ))^2 ))/(2n tan〖(180°)/n〗 (l/2+P/(2n tan〖(180°)/n〗 )) )
R_1=b^2/2h=(2l^2+P^2/n^2 )/(2√(l^2-(P/(2n tan〖(180°)/n〗 ))^2 ))
Как найти периметр основания правильной треугольной пирамиды
Содержание
- Формулы для правильной пирамиды.
- Правильная треугольная пирамида.
- Формулы для правильной треугольной пирамиды.
- Этот видеоурок доступен по абонементу
- Пирамида, основные понятия и элементы
- Площадь основания пирамиды, площади основных правильных многоугольников
- Площадь боковой поверхности пирамиды
- Связь площади треугольника с площадью его проекции
- Решение задач
Правильная пирамида обладает следующими свойствами:
Формулы для правильной пирамиды.
V — объем пирамиды,
S — площадь основания пирамиды,
h — высота пирамиды,
Sb — площадь боковой поверхности пирамиды,
a — апофема (не путать с α) пирамиды,
P — периметр основания пирамиды,
n — число сторон основания пирамиды,
b — длина бокового ребра пирамиды,
α — плоский угол при вершине пирамиды.
Ниже указанная формула определения объема используется лишь для правильной пирамиды:
V — объем правильной пирамиды,
h — высота правильной пирамиды,
n — количество сторон правильного многоугольника, основания правильной пирамиды,
a — длина стороны правильного многоугольника.
Боковое ребро правильной пирамиды находят по формуле:
где b — боковое ребро правильной пирамиды (SA, SB, SC, SD либо SE),
n — количество сторон правильного многоугольника (основание правильной пирамиды),
a — сторона правильного многоугольника (AB, BC, CD, DE либо EA) — основания правильной пирамиды,
h — высота правильной пирамиды (OS).
Указания к решению задач. Свойства, которые мы перечислили выше, помогают при практическом решении. Когда нужно определить углы наклона граней, их поверхность и так далее, значит общая методика сводится к разбиению всей объемной фигуры на отдельные плоские фигуры и применение их свойств для определения отдельных элементов пирамиды, так как большинство элементов оказываются общими для нескольких фигур.
Нужно разбить всю объемную фигуру на отдельные элементы — треугольники, квадраты, отрезки. Дальше, к отдельным элементам применяем знания из курса планиметрии, что очень упрощает определение ответа.
Правильная треугольная пирамида.
Правильная треугольная пирамида — это пирамида, у которой основанием оказывается правильный треугольник, а вершина опускается в центр основания.
Формулы для правильной треугольной пирамиды.
Формула для нахождения объема правильной треугольной пирамиды:
V — объем правильной пирамиды, которая имеет в основании правильный (равносторонний) треугольник,
h — высота правильной пирамиды,
a — длина стороны основания правильной пирамиды.
Так как правильная треугольная пирамида — это частный случай правильной пирамиды, значит, формулы, верные для правильной пирамиды, оказываются верными и для правильной треугольной.
Еще одним частным случаем правильно пирамиды является тетраэдр.
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
Пирамида, основные понятия и элементы
Вспомним понятие n-угольной пирамиды. Она получается следующим образом: в плоскости .</p>
<p style=)
Определение.
Многогранник 
Площадь поверхности пирамиды состоит из площади боковой поверхности и площади основания:
Площадь основания пирамиды, площади основных правильных многоугольников
Рассмотрим нахождение площади основания правильной n-угольной пирамиды. Правильный n-угольник, как нам известно, имеет равные стороны и равные внутренние углы. Решим следующую задачу: для n-угольника с заданной длиной стороны (
) и количеством углов (n) найти площадь (рисунок 2).
Рис. 2. Нахождение площади n-угольника
Рассмотрим треугольник 
Половина этого угла, угол 
.
Треугольник , то по соотношениям в прямоугольном треугольнике мы легко найдем все остальные элементы.</p>
<p style=)
Чтобы найти площадь n-угольника, нужно сложить n площадей треугольников вида 
Площадь треугольника определяется по формуле:
Теперь получим площадь всего n-угольника:
Рассмотрим наиболее распространенные частные случаи:
Площадь правильного треугольника:
Площадь правильного шестиугольника:
Чтобы нарисовать правильный шестиугольник, удобно пользоваться следующим алгоритмом (рисунок 3):
Построить окружность (зеленая пунктирная линия) Провести диаметр (синяя пунктирная линия) Отметить середины радиусов построенного диаметра Провести через середины перпендикуляры (красные пунктирные линии) Получены вершины шестиугольника – построить шестиугольник.
Рис. 3. Правильный шестиугольник
Чтобы найти площадь правильного шестиугольника действуем стандартным методом. Рассматриваем треугольник АОС, в нем находим угол ∠АОВ, таких углов шесть, имеем:
Поскольку отрезки ОА и ОВ равны, то углы ∠ОАВ и ∠ОВА также составляют по 
. Так, рассматриваемый треугольник правильный. Его площадь нам известна:
Площадь шестиугольника состоит из шести таких площадей:
Площадь боковой поверхности пирамиды
Рассмотрим нахождение площади боковой поверхности правильной пирамиды.
Где 
Рис. 4. Иллюстрация к задаче 1
Задана правильная пирамида с вершиной Р и основанием АВС. РН – высота пирамиды, РО – апофема. Сторона основания равняется 
По вышеприведенной формуле для того, чтобы найти площадь боковой поверхности пирамиды, необходимо найти ее апофему и полупериметр основания. Периметр основания нам известен, так как задана сторона основания. Найдем апофему из прямоугольного треугольника РНО. Один из катетов задан по условию – 
. Найдем второй катет ОН, он соответствует радиусу вписанной в треугольник окружности, формула нам известна:
Найдем апофему по теореме Пифагора:
Теперь можем найти площадь боковой поверхности пирамиды:
Связь площади треугольника с площадью его проекции
Площадь боковой поверхности и площадь основания пирамиды связаны через величину двугранного угла при основании.
Решение задач
Задача 2
РН – перпендикуляр к плоскости треугольника АВН. Из точки Н опущен перпендикуляр НМ к прямой АВ. 
. Доказать:
Решение. Проиллюстрируем условие:
Рис. 5. Иллюстрация к задаче 2
Треугольник АВН – это проекция треугольника АВР. Нужно доказать, что площадь проекции есть площадь исходного треугольника на косинус двугранного угла между ними. Поскольку НМ – перпендикуляр к АВ, то и РМ – перпендикуляр к АВ по теореме о трех перпендикулярах. Значит, угол 
– это линейный угол двугранного угла с ребром АВ. АВР – часть боковой поверхности, АВН – часть основания.
Найдем отношение площадей интересующих нас треугольников:
Рассмотрим прямоугольный треугольник РНМ. В нем РМ – гипотенуза, НМ – катет, прилежащий к заданному углу 
. Отсюда заключаем:
Что и требовалось доказать.
Задача 3
Доказать для правильной треугольной пирамиды: 
Рис. 6. Иллюстрация к задаче 3
Задана правильная треугольная пирамида РАВС с основанием АВС и вершиной Р. 
– линейный угол двугранного угла с ребром АВ, точкой Р в одной плоскости и точкой С в другой плоскости.
Очевидно, что угол наклона 
В задаче 2 мы доказали: 
.
Выполним сложение полученных выражений.
Что и требовалось доказать.
Задача 4
Боковые грани пирамиды РАВС наклонены к основанию под одним и тем же углом 
Рис. 7. Иллюстрация к задаче 4
Пусть РО – высота пирамиды. Найдем место расположения точки О. Из точки О опустим перпендикуляры к сторонам треугольника АВС – 
.
Поскольку :</p>
<p style=)
Выполним сложение полученных выражений.
Что и требовалось доказать.
Итак, мы рассмотрели площадь поверхности пирамиды, в частности, площадь основания и площадь боковой поверхности, следующий урок будет посвящен задачам.
Список литературы
- И. М. Смирнова, В. А. Смирнов. Геометрия. 10-11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. – 5-е изд., испр. и доп. – М.: Мнемозина, 2008. – 288 с.: ил.
- Шарыгин И. Ф. Геометрия. 10-11 класс: Учебник для общеобразовательных учебных заведений / Шарыгин И. Ф. – М.: Дрофа, 1999. – 208 с.: ил.
- Е. В. Потоскуев, Л. И. Звалич. Геометрия. 10 класс: Учебник для общеобразовательных учреждений с углубленным и профильным изучением математики /Е. В. Потоскуев, Л. И. Звалич. – 6-е изд., стереотип. – М.: Дрофа, 2008. – 233 с.: ил.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
Домашнее задание
- Задача 1: основанием пирамиды является квадрат, одно из боковых ребер перпендикулярно основанию. Плоскость боковой грани, не проходящей через высоту пирамиды, наклонена к плоскости основания под углом Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.
Оценка статьи:
Загрузка…
Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта. 
Загрузка…Пирамида — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину. По числу углов основания различают пирамиды треугольные (тетраэдр), четырёхугольные и т. д. Пирамида является частным случаем конуса.
Пирамида называется правильной, если основанием её является правильный многоугольник, а вершина проецируется в центр основания. Тогда она обладает такими свойствами:
- боковые рёбра правильной пирамиды равны;
- в правильной пирамиде все боковые грани — конгруэнтные равнобедренные треугольники;
- в любую правильную пирамиду можно как вписать, так и описать вокруг неё сферу;
- если центры вписанной и описанной сферы совпадают, то сумма плоских углов при вершине пирамиды равна Пи, а каждый из них соответственно Пи/n, где n — количество сторон многоугольника основания;
- площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Пирамида называется прямоугольной, если одно из боковых рёбер пирамиды перпендикулярно основанию. В данном случае, это ребро и является высотой пирамиды.
Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.
людей нашли эту статью полезной. А Вы?
Расчет площади, периметра и объема пирамиды
Поиск для:
Пирамида — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину. По числу углов основания различают пирамиды треугольные (тетраэдр), четырёхугольные и т. д. Пирамида является частным случаем конуса.
Треугольная пирамида
Площадь основания: ½as
Площадь поверхности пирамиды: ½as + (3/2)sl
Объем пирамиды: (1/6)abh
| Введите длину апофемы | |
| Введите длину стороны | |
| Диагональ | |
| Введите высоту | |
| Площадь основания | |
| Периметр | |
| Объем пирамиды |
Квадратная пирамида
Площадь основания: s²
Периметр: s² + 2sl
Объем пирамиды: (1/3)b²h
| Введите длину стороны | |||
| Диагональ | |||
| Введите высоту | |||
| Площадь основания | |||
| Периметр | |||
| Объем пирамиды |
Пятиугольная пирамида
Площадь основания: (5/2)as
Периметр: (5/2)as + (5/2)sl
Объем пирамиды: (5/6)abh
| Введите длину апофемы | |
| Введите длину стороны | |
| Диагональ | |
| Введите высоту | |
| Площадь основания | |
| Периметр | |
| Объем пирамиды |
Шестигранная пирамида
Площадь основания: (6/2)as
Периметр: 3as + 3sl
Объем пирамиды:abh
| Введите длину апофемы | |
| Введите длину стороны | |
| Диагональ | |
| Введите высоту | |
| Площадь основания | |
| Периметр | |
| Объем пирамиды |
Пирамида называется правильной, если основанием её является правильный многоугольник, а вершина проецируется в центр основания. Тогда она обладает такими свойствами:
- боковые рёбра правильной пирамиды равны;
- в правильной пирамиде все боковые грани — конгруэнтные равнобедренные треугольники;
- в любую правильную пирамиду можно как вписать, так и описать вокруг неё сферу;
- если центры вписанной и описанной сферы совпадают, то сумма плоских углов при вершине пирамиды равна Пи, а каждый из них соответственно Пи/n, где n — количество сторон многоугольника основания;
- площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Пирамида называется прямоугольной, если одно из боковых рёбер пирамиды перпендикулярно основанию. В данном случае, это ребро и является высотой пирамиды.
Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.
людей нашли эту статью полезной. А Вы?
Площадь боковой поверхности пирамиды — формула, пример расчета
Пирамида – это многогранная фигура, в основании которой лежит многоугольник, а остальные грани представлены треугольниками с общей вершиной.
Если в основании лежит квадрат, то пирамиду называется
четырехугольной, если треугольник – то треугольной. Высота пирамиды проводится из ее вершины перпендикулярно основанию. Также для расчета площади используется апофема – высота боковой грани, опущенная из ее вершины.
Формула площади боковой поверхности пирамиды представляет собой сумму площадей ее боковых граней, которые равны между собой. Однако этот способ расчета применяется очень редко. В основном площадь пирамиды рассчитывается через периметр основания и апофему:
Рассмотрим пример расчета площади боковой поверхности пирамиды.
Пусть дана пирамида с основанием ABCDE и вершиной F. AB=BC=CD=DE=EA=3 см. Апофема a = 5 см. Найти площадь боковой поверхности пирамиды.
Найдем периметр. Так как все грани основания равны, то периметр пятиугольника будет равен:
Теперь можно найти боковую площадь пирамиды:
Площадь правильной треугольной пирамиды
Правильная треугольная пирамида состоит из основания, в котором лежит правильный треугольник и трех боковых граней, которые равны по площади.
Формула площади боковой поверхности правильной треугольной пирамиды может быть рассчитана разными способами. Можно применить обычную формулу расчета через периметр и апофему, а можно найти площадь одной грани и умножить ее на три. Так как грань пирамиды – это треугольник, то применим формулу площади треугольника. Для нее потребуется апофема и длина основания. Рассмотрим пример расчета площади боковой поверхности правильной треугольной пирамиды.
Дана пирамида с апофемой a = 4 см и гранью основания b = 2 см. Найдите площадь боковой поверхности пирамиды.
Для начала находим площадь одной из боковых граней. В данном случае она будет:
Подставляем значения в формулу:
Так как в правильной пирамиде все боковые стороны одинаковы, то площадь боковой поверхности пирамиды будет равна сумме площадей трех граней. Соответственно:
Площадь усеченной пирамиды
Усеченной пирамидой называется многогранник, который образовывается пирамидой и ее сечением, параллельным основанию.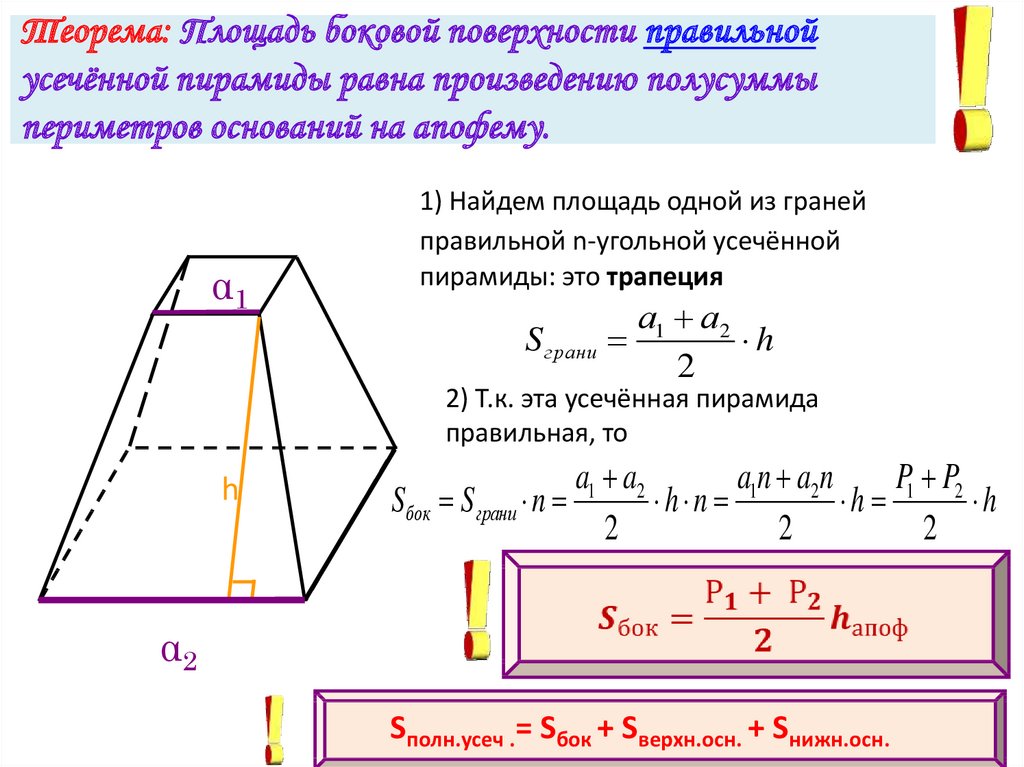
Формула площади боковой поверхности усеченной пирамиды очень проста. Площадь равняется произведению половины суммы периметров оснований на апофему:
Рассмотрим пример расчета площади боковой поверхности усеченной пирамиды.
Дана правильная четырехугольная пирамида. Длины основания равны b = 5 см, c = 3 см. Апофема a = 4 см. Найдите площадь боковой поверхности фигуры.
Для начала найдем периметр оснований. В большем основании он будет равен:
В меньшем основании:
Посчитаем площадь:
Таким образом, применив несложные формулы, мы нашли площадь усеченной пирамиды.
Похожие записи
Поделиться
Подрубрика Геометрия, Рубрика Математика.
Другие статьи по теме
Видео-вопрос: нахождение периметра основания пирамиды по ее объему и высоте
Зная, что квадратная пирамида имеет объем 372 см³ и высоту 31 см, определите периметр ее основания.
Стенограмма видео
Учитывая, что квадратная пирамида имеет
объемом 372 кубических сантиметра и высотой 31 сантиметр, определяют
периметр его основания.
Нам не дали схему
здесь, но иногда может быть полезно сделать набросок. Во-первых, нам говорят, что это
квадратная пирамида, поэтому мы будем знать, что длина и ширина будут точно такими же
замер на базе. Нам дан объем
пирамида как 372 кубических сантиметра, и нам дана перпендикулярная высота как 31
сантиметры. Напомним, что объем
пирамида равна одной трети произведения площади основания на перпендикуляр
высота. Мы можем использовать тот факт, что мы
зная объем пирамиды и ее перпендикулярную высоту, найти площадь
база. Это позволит нам затем
рассчитать периметр основания.
Мы можем подставить значения
тогда. Объем 372, а высота
31, чтобы получить 372, равно одной трети площади основания, умноженной на 31. Умножив обе части на три, мы
1116 равно площади основания, умноженной на 31. Затем мы делим обе стороны на 31, чтобы получить
дайте нам площадь основания 36 квадратных сантиметров. Итак, как нам перейти от знания
площади основания этой пирамиды, чтобы найти ее периметр? Ну, помните, что база
квадрат. Итак, если мы определим длину одного
сторона равна 𝑙, то все остальные стороны будут иметь длину 𝑙. Площадь квадрата будет
рассчитывается как 𝑙 в квадрате. В этом случае 𝑙 в квадрате должно быть
дали нам 36. Чтобы вычислить 𝑙, мы взяли бы
квадратный корень из обеих сторон, а квадратный корень из 36 равен шести. И, конечно же, единицы длины
будет в сантиметрах.
Чтобы найти периметр, это
расстояние вокруг внешнего края.
Мы могли бы добавить шесть и шесть и шесть
а шесть или больше просто равняются шести умножить на четыре, что дало бы нам значение
24. А поскольку периметр все-таки
длина, то у нас были бы единицы измерения в сантиметрах. Итак, мы обнаружили, что периметр
основания этой пирамиды составляет 24 сантиметра, и мы сделали это, используя объем на
сначала вычислить площадь основания.
Nagwa использует файлы cookie, чтобы обеспечить вам максимальное удобство на нашем веб-сайте. Узнайте больше о нашей Политике конфиденциальности.
Площадь поверхности пирамиды – формула, определение и примеры
Площадь поверхности пирамиды получается путем сложения площадей всех ее граней. Пирамида — это трехмерная фигура, основанием которой является многоугольник, а боковые грани (треугольники) сходятся в точке, называемой вершиной (или вершиной).
Перпендикулярное расстояние от вершины до центра основания называется высотой или высотой пирамиды. Длина перпендикуляра, проведенного от вершины к основанию треугольника (боковой грани), называется «наклонной высотой». Давайте узнаем больше о площади поверхности пирамиды вместе с ее формулой, несколькими решенными примерами и практическими вопросами.
| 1. | Какова площадь поверхности пирамиды? |
| 2. | Площадь поверхности пирамиды Формула |
| 3. | Доказательство площади поверхности пирамиды Формула |
| 4. | Часто задаваемые вопросы о площади поверхности пирамиды |
Какова площадь поверхности пирамиды?
площадь поверхности пирамиды является мерой общей площади, занимаемой всеми ее гранями. Посмотрите на приведенную ниже пирамиду, чтобы увидеть все ее грани и другие части, такие как вершина, высота, наклонная высота и основание.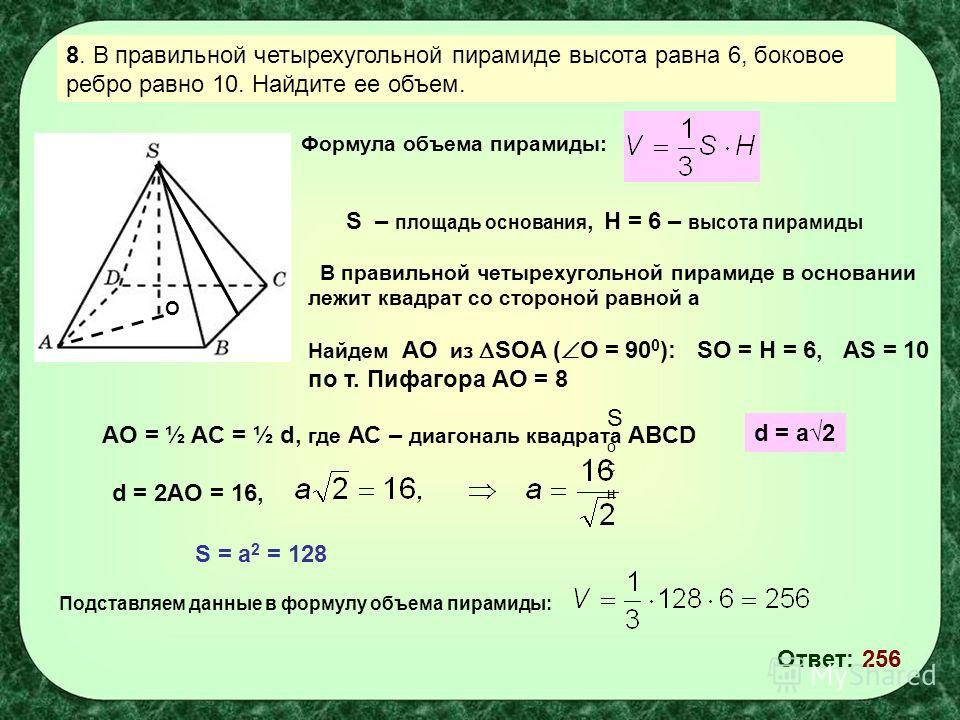
Площадь поверхности пирамиды представляет собой сумму площадей ее граней и, следовательно, измеряется в квадратных единицах, таких как м 2 , см 2 , дюймы
2 , футы 2 и т. д. Пирамида имеет два типа площадей поверхности: площадь боковой поверхности (LSA) и общая площадь поверхности (TSA).
- Площадь боковой поверхности (LSA) пирамиды = сумма площадей боковых граней (треугольников) пирамиды.
- Общая площадь поверхности (TSA) пирамиды = LSA пирамиды + площадь основания
В целом, площадь поверхности пирамиды без каких-либо указаний относится к общей площади поверхности пирамиды.
Площадь поверхности пирамиды Формула
Площадь поверхности пирамиды можно вычислить, найдя площади каждой из ее граней и сложив их. Если пирамида правильная (т. Е. Пирамида, основание которой представляет собой правильный многоугольник, а высота проходит через центр основания), есть некоторые специальные формулы для нахождения площади боковой поверхности и общей площади поверхности.
Рассмотрим правильную пирамиду, периметр основания которой равен «P», площадь основания — «B», а наклонная высота (высота каждого треугольника) — «l». Затем
- Площадь боковой поверхности пирамиды (LSA) = (1/2) Pl
- Общая площадь поверхности пирамиды (TSA) = LSA + площадь основания = (1/2) Pl + B
Обратите внимание, что здесь мы будем использовать формулы площади полигонов для расчета базовых площадей. Теперь давайте посмотрим, как вывести формулы площади поверхности пирамиды.
Доказательство площади поверхности пирамиды Формула
Площадь поверхности пирамиды включает периметр и наклонную высоту. Давайте разберемся с формулами LSA и TSA пирамиды на примере конкретной пирамиды. Рассмотрим квадратную пирамиду, длина основания которой равна «а», а высота наклона равна «l».
Тогда
- Площадь основания (площадь квадрата) пирамиды равна, B = a 2
- Периметр основания (периметр квадрата) пирамиды равен, P = 4a
- Площадь каждой из боковых граней (площадь треугольника) = (1/2) × основание × высота = (1/2) × (a) × l
Следовательно, сумма всех боковых граней (сумма всех 4-х треугольных граней) = 4 [(1/2) × (a) × l] = (1/2) × (4a) × l = (1/2 ) пл.
(Здесь мы заменили 4a на P, который представляет его периметр.)
Следовательно, площадь боковой поверхности пирамиды (LSA) = (1/2) Pl
Мы знаем, что общая площадь поверхности пирамиды (TSA) получается путем сложения площадей основания и боковой поверхности. Таким образом,
Общая площадь поверхности пирамиды (TSA) = LSA + площадь основания = (1/2) Pl + B
Используя эти две формулы, мы можем вывести формулы площади поверхности различных типов пирамид.
Площадь поверхности пирамиды с указанием высоты
Площадь поверхности пирамиды можно рассчитать, если известна ее высота. Обратите внимание на приведенный ниже рисунок, который показывает, что треугольник, образованный половиной длины стороны основания (a/2), наклонной высоты (l) и высоты (h), является прямоугольным треугольником. Следовательно, мы можем применить теорему Пифагора и узнать наклонную высоту, если известны высота и длина основания. Таким образом, л 2 = h 2 + (a/2) 2
Итак, мы можем рассчитать наклонную высоту по формуле l 2 = h 2 + (062) 2 90 .
Теперь, когда у нас есть наклонная высота, длина основания и высота, мы можем найти площадь поверхности пирамиды, используя формулу Общая площадь поверхности пирамиды (TSA) = LSA + площадь основания = (1/2) Pl + B
☛ Связанные статьи
- Площадь поверхности прямоугольного параллелепипеда
- Площадь поверхности цилиндра
- Площадь поверхности призмы
- Площадь поверхности конуса
- Площадь поверхности сферы
- Разница между площадью и площадью поверхности
- Формулы площади поверхности
- Площадь поверхности куба
Примеры площади поверхности пирамиды
-
Пример 1: Рассчитайте площадь боковой поверхности квадратной пирамиды, если длина стороны основания составляет 14 дюймов, а наклонная высота пирамиды составляет 20 дюймов.
Решение:
Длина стороны основания, a = 14 дюймов
Тогда периметр основания (квадрата) равен P = 4a = 4(14) = 56 дюймов.
Наклонная высота, l = 20 дюймов
Площадь боковой поверхности квадратной пирамиды,
Площадь боковой поверхности (LSA) = (1/2) Pl
= (1/2) × (56) × 20
= 560 в 2
Следовательно, площадь боковой поверхности данной пирамиды равна 560 в 2 .
-
Пример 2: Укажите истинное или ложное значение.
а.) Площадь поверхности любой пирамиды можно вычислить, найдя площади каждой из ее граней и сложив их.
b.) Общая площадь поверхности (TSA) пирамиды = площадь боковой поверхности (LSA) пирамиды
Решение:
a.) Действительно, площадь поверхности любой пирамиды можно вычислить, найдя области каждой из его граней и их сложение.
b.) Неверно, общая площадь поверхности (TSA) пирамиды = площадь боковой поверхности (LSA) пирамиды + площадь основания
-
Пример 3: Рассчитайте общую площадь поверхности квадратной пирамиды, если сторона основания равна 14 дюймам, а высота пирамиды равна 24 дюймам.
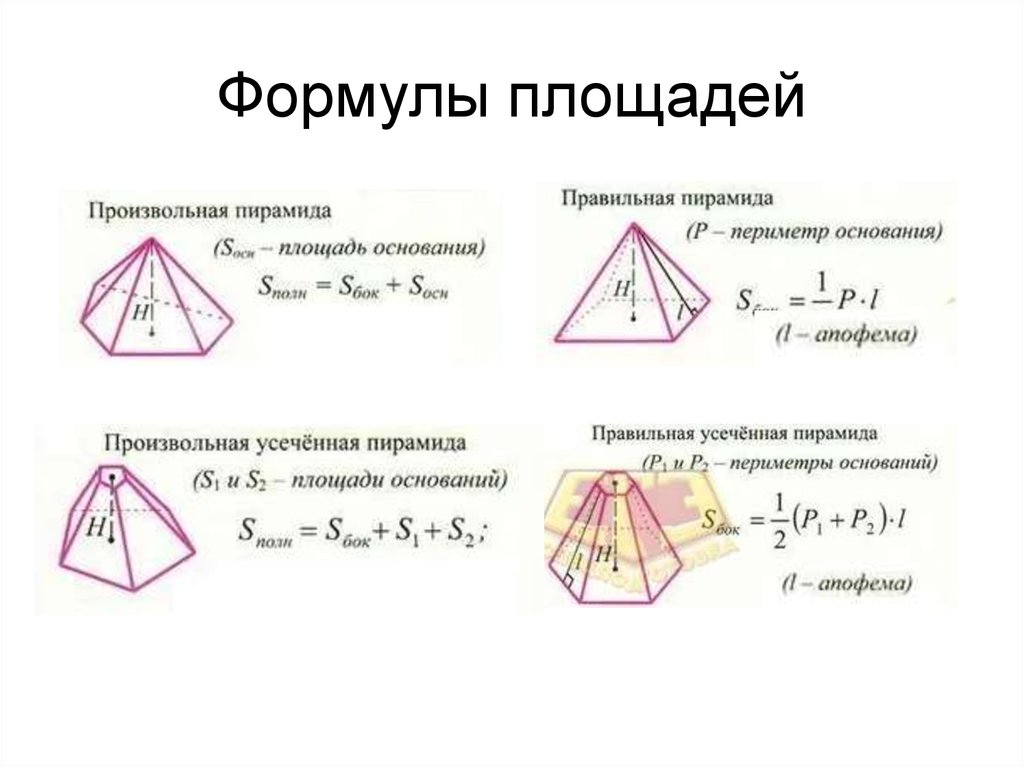
Решение:
Дана сторона основания a = 14 дюймов, а высота пирамиды h = 24 дюйма.
Пусть его наклонная высота будет ‘l’.
По теореме Пифагора, l 2 = (a/2) 2 + h 2
l 2 = (14/2) 2 + 24 2 = 625
Таким образом, l = 25 дюймов.
Периметр основания равен P = 4a = 4(14) = 56 дюймов.
Базовая площадь, B = 14 2 = 196 квадратных дюймов.
Общая площадь поверхности квадратной пирамиды равна,
TSA = (1/2) Pl + B, где B = 196, P = 56, l = 25 25] + 196 = 896 квадратных дюймов
Следовательно, TSA данной пирамиды = 896 квадратных дюймов.
перейти к слайдуперейти к слайдуперейти к слайду
Хотите создать прочную основу в математике?
Выйдите за рамки запоминания формул и поймите «почему», стоящее за ними. Испытайте Cuemath и приступайте к работе.
Записаться на бесплатный пробный урок
Практические вопросы по площади поверхности пирамиды
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о площади поверхности пирамиды
Что такое определение площади поверхности пирамиды?
Площадь поверхности пирамиды определяется как сумма площадей всех ее граней.
Существует два типа площадей поверхности: общая площадь поверхности (TSA), представляющая собой сумму площадей всех граней, и площадь боковой поверхности (LSA), представляющая собой сумму площадей сторон. лица.
Какова общая площадь поверхности пирамиды?
Общая площадь поверхности пирамиды получается путем сложения площадей всех ее граней (и основания, и боковых граней). Общая площадь поверхности пирамиды, периметр основания которой равен «P», площадь основания — «B», а наклонная высота — «l», рассчитывается по формуле TSA = (1/2) Pl + B.
Какова площадь боковой поверхности пирамиды?
Площадь боковой поверхности пирамиды равна сумме площадей всех ее боковых граней (треугольников). Площадь боковой поверхности пирамиды рассчитывается по формуле LSA = (1/2) Pl, где P — периметр основания, а l — наклонная высота.
Какова формула площади поверхности пирамиды?
Существует два типа площадей поверхности пирамиды: общая площадь поверхности и площадь боковой поверхности.
Формула, которая используется для нахождения этих двух площадей, приведена ниже.
- Общая площадь поверхности = (1/2) Pl + B
- Площадь боковой поверхности = (1/2) Pl
, где «B» — площадь основания, «l» — высота наклона, а «P» — периметр основания.
Как найти площадь поверхности пирамиды с наклонной высотой?
Формула, используемая для определения площади поверхности пирамиды, может быть рассчитана с использованием наклонной высоты. Его общую площадь поверхности можно рассчитать по формуле (1/2) Pl + B. Рассмотрим пирамиду, высота наклона которой равна «l», периметр основания равен «P», а площадь основания равна «B». Площадь основания можно найти, применяя формулы площади многоугольника.
Как найти площадь поверхности пирамиды с высотой (или высотой)?
Площадь поверхности пирамиды можно рассчитать, если известна высота. Рассмотрим пирамиду, основание которой представляет собой правильный многоугольник со стороной «а», наклонная высота пирамиды равна «l», а высота равна «h».
Примечание. Если Вам необходимо решить задачу по геометрии, которой здесь нет – пишите об этом в форуме. В задачах вместо символа “квадратный корень” применяется функция sqrt(), в которой sqrt – символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак “√”.
Задача.
Боковая грань правильной треугольной пирамиды представляет собой правильный треугольник, площадь которого 16 корней из 3 см2 (16√3). Вычислить периметр основания пирамиды.
Решение.
Правильный треугольник – это равносторонний треугольник. Соответственно, боковая грань пирамиды представляет собой равносторонний треугольник.
Площадь равностороннего треугольника равна:
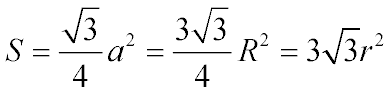
Соответственно:
16√3 = a2 √3 / 4
16 = a2 / 4
a2 = 64
a = 8 см
Основанием правильной треугольной пирамиды является правильный (равносторонний) треугольник. Таким образом, периметр основания пирамиды равен
8 * 3 = 24 см
Ответ: 24 см.
0
Правильная треугольная пирамида (правильная пирамида с треугольником в основании). Тетраэдр |
Описание курса
| Объем правильной треугольной пирамиды
