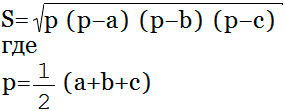Как найти периметр по формуле герона

Как найти периметр по формуле герона

Периметр треугольника формула герона

Как найти периметр треугольника

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение

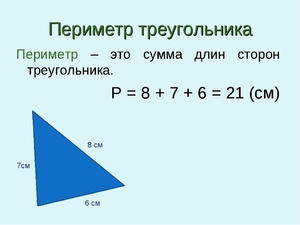
Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской буквой P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах и ходе решении.

Важно, чтобы все параметры были переданы в одной единице длины, иначе мы не сможем подсчитать результат. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

В чем измеряется периметр:

Как узнать периметр треугольника

Рассмотрим какие существуют формулы, и при каких известных исходных данных их можно применять.

Если известны три стороны, то периметр треугольника равен их сумме. Этот способ проходят во втором классе.

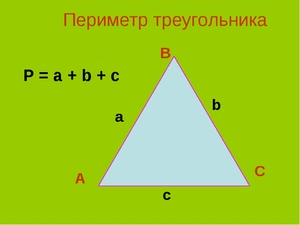
P = a + b + c, где a, b, c — длина стороны.

Если известна площадь и радиус вписанной окружности:

P = 2 * S : r, где S — площадь, r — радиус вписанной окружности.

Если известны две стороны и угол между ними, вычислить периметр треугольника можно так:

P = √ b 2 + с 2 — 2 * b * с * cosα + (b + с), где b, с — известные стороны, α — угол между известными сторонами.

Если известна одна сторона в равностороннем треугольнике:

P = 3 * a, где a — длина стороны.

Все стороны в равносторонней фигуре равны.

Если известна боковая сторона и основание в равнобедренном треугольнике:

P = 2 * a + b, где a — боковая сторона, b — основание.

Боковые стороны в равнобедренной фигуре равны.

Если известна боковая сторона и высота в равнобедренном треугольнике:

P = 2 * (√ a 2 + h 2 ) + 2 * a, где a — боковая сторона, h — высота.

Высотой принято называть отрезок, который вышел из вершины и опустился на основание. В равнобедренной фигуре высота делит основание пополам.

Если известны катеты в прямоугольном треугольнике:

P = √ a 2 + b 2 + (a + b), где a, b — катеты.

Катет — одна из двух сторон, которые образуют прямой угол.

Если известны катет и гипотенуза в прямоугольном треугольнике:

P = √ c 2 — a 2 + (a + c), где a — любой катет, c — гипотенуза.

Гипотенуза — сторона, которая лежит напротив прямого угла.

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Формула Герона для треугольника

В данной публикации мы рассмотрим формулу Герона, пользуясь которой можно найти площадь треугольника. Также разберем примеры решения задач для того, чтобы закрепить представленный материал.

Формула площади

Площадь треугольника ( S ) равняется квадратному корню из произведения его полупериметра ( p ) на разности полупериметра и каждой из его сторон ( a, b, c ).

Полупериметр ( p ) вычисляется таким образом:

Примечание: для использования формулы необходимо знать/найти длину всех сторон треугольника.

Формула получила такое название в честь греческого математика и механика Герона Александрийского, который изучал треугольники с целочисленными сторонами и площадью (героновские). К таким, например, относится прямоугольный треугольник с соотношением сторон 3:4:5, который также называют египетским.

Примеры задач

Задание 1
Найдите площадь треугольника со сторонами 6, 8 и 10 см.

Решение
Для начала найдем полупериметр:
p = (6 + 8 + 10) / 2 = 12 см.

Теперь воспользуемся формулой Герона, подставив в нее заданные значения:
= .

Задание 2
В прямоугольном треугольнике длина гипотенузы равняется 15 см, а одного из катетов – 9 см. Вычислите площадь фигуры.

Решение
Пусть гипотенуза – это c , известный катет – a , а неизвестный – b .

Применим Теорему Пифагора, чтобы найти длину катета b :
b 2 = = = , следовательно,

Полупериметр треугольника равен:
p = (9 + 12 + 15) / 2 = 18 см.

Остается только использовать формулу для нахождения площади:
= = .

Формула Герона для нахождения площади треугольника

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы рассмотрим еще один способ вычисления площади треугольника – с помощью формулы Герона. Она позволяет вычислить площадь треугольника, зная лишь его стороны, что может очень пригодиться, особенно в практических вычислениях. Мы выпишем и докажем формулу Герона, а также решим несколько задач на применение этой формулы.

Формула Герона для треугольника

В данной публикации мы рассмотрим формулу Герона, пользуясь которой можно найти площадь треугольника. Также разберем примеры решения задач для того, чтобы закрепить представленный материал.

Формула площади

Площадь треугольника ( S ) равняется квадратному корню из произведения его полупериметра ( p ) на разности полупериметра и каждой из его сторон ( a, b, c ).

Полупериметр ( p ) вычисляется таким образом:

Примечание: для использования формулы необходимо знать/найти длину всех сторон треугольника.

Формула получила такое название в честь греческого математика и механика Герона Александрийского, который изучал треугольники с целочисленными сторонами и площадью (героновские). К таким, например, относится прямоугольный треугольник с соотношением сторон 3:4:5, который также называют египетским.

Примеры задач

Задание 1
Найдите площадь треугольника со сторонами 6, 8 и 10 см.

Решение
Для начала найдем полупериметр:
p = (6 + 8 + 10) / 2 = 12 см.

Теперь воспользуемся формулой Герона, подставив в нее заданные значения:
= .

Задание 2
В прямоугольном треугольнике длина гипотенузы равняется 15 см, а одного из катетов – 9 см. Вычислите площадь фигуры.

Решение
Пусть гипотенуза – это c , известный катет – a , а неизвестный – b .

Применим Теорему Пифагора, чтобы найти длину катета b :
b 2 = = = , следовательно,

Полупериметр треугольника равен:
p = (9 + 12 + 15) / 2 = 18 см.

Остается только использовать формулу для нахождения площади:
= = .

Площадь треугольника по формуле Герона

Герон Александрийский (др.-греч. Ἥρων ὁ Ἀλεξανδρεύς)
) – греческий математик и механик. Герона относят к величайшим инженерам за всю историю человечества. Он первым изобрёл автоматические двери, автоматический театр кукол, автомат для продаж, скорострельный самозаряжающийся арбалет, паровую турбину, автоматические декорации,

прибор для измерения протяжённости дорог (древний одометр) и др. Первым начал создавать программируемые устройства (вал со штырьками с намотанной на него верёвкой).

Треугольник образуется соединением отрезками трех точек, не лежащих на одной прямой. При этом точки называются вершинами треугольника, а отрезки – его сторонами.

Формула Герона:

a, b, c – это стороны треугольника.

Онлайн калькулятор для вычисления площади треугольника по формуле Герона.

[spoiler title=”источники:”]

Формула Герона для треугольника

http://allcalc.ru/node/781

[/spoiler]

Источник

Фо́рмула Герона — формула для вычисления площади треугольника S по длинам его сторон a,b,c:

{displaystyle S={sqrt {p(p-a)(p-b)(p-c)}}},

где p — полупериметр треугольника: {displaystyle p={tfrac {1}{2}}cdot (a+b+c)}.

Формула содержится в «Метрике» Герона Александрийского (I век н. э.) и названа в его честь (хотя она была известна ещё Архимеду). Герон интересовался треугольниками с целочисленными сторонами, площади которых тоже являются целыми, такие треугольники носят название героновых, простейшим героновым треугольником является египетский треугольник.

Доказательство 1 (тригонометрическое):

Доказательство 2 (на основе теоремы Пифагора):

Треугольник со сторонами a, b, c и высотой

h, разделяющей основание

c на

d и (c − d).

По теореме Пифагора имеем следующие равенства для гипотенуз: a2 = h2 + (c − d)2 и b2 = h2 + d2 — см. рисунок справа. Вычитая из первого равенства второе, получаем a2 − b2 = c2 − 2cd. Это уравнение позволяет нам выразить d через стороны треугольника:

{displaystyle d={frac {-a^{2}+b^{2}+c^{2}}{2c}}}

Для высоты h у нас было равенство h2 = b2 − d2, в которое можно подставить полученное выражение для d и применить формулы для квадратов:

{displaystyle {begin{aligned}h^{2}&=b^{2}-left({frac {-a^{2}+b^{2}+c^{2}}{2c}}right)^{2}={frac {(2bc-a^{2}+b^{2}+c^{2})(2bc+a^{2}-b^{2}-c^{2})}{4c^{2}}}\&={frac {((b+c)^{2}-a^{2})(a^{2}-(b-c)^{2})}{4c^{2}}}={frac {(b+c-a)(b+c+a)(a+b-c)(a-b+c)}{4c^{2}}}\end{aligned}}}

Замечая, что {displaystyle b+c-a=2p-2a}, a+b+c=2p, a+b-c=2p-2c, {displaystyle a-b+c=2p-2b}, получаем:

{displaystyle {begin{aligned}h^{2}&={frac {2(p-a)cdot 2pcdot 2(p-c)cdot 2(p-b)}{4c^{2}}}={frac {4p(p-a)(p-b)(p-c)}{c^{2}}}end{aligned}}}

Используя основное равенство для площади треугольника {displaystyle S={frac {ch}{2}}} и подставляя в него полученное выражение для h, в итоге имеем:

{displaystyle {begin{aligned}S={sqrt {{frac {c^{2}}{4}}cdot {frac {4p(p-a)(p-b)(p-c)}{c^{2}}}}}={sqrt {p(p-a)(p-b)(p-c)}}end{aligned}}}

ч.т.д.

Вариации и обобщения[править | править код]

  • Формулу Герона можно записать с помощью определителя в виде[1]:
    -16S^{2}={begin{vmatrix}0&a^{2}&b^{2}&1\a^{2}&0&c^{2}&1\b^{2}&c^{2}&0&1\1&1&1&0end{vmatrix}}={begin{vmatrix}a&b&c&0\b&a&0&c\c&0&a&b\0&c&b&aend{vmatrix}}
Первый определитель последней формулы является частным случаем определителя Кэли — Менгера[en] для вычисления гиперобъёма симплекса.
через длины высот h_{a}, h_{b} и h_{c} и полусумму их обратных величин H=(h_{a}^{-1}+h_{b}^{-1}+h_{c}^{-1})/2[3]:

S^{-1}=4{sqrt {H(H-h_{a}^{-1})(H-h_{b}^{-1})(H-h_{c}^{-1})}};
через углы треугольника alpha , beta и gamma , полусумму их синусов {displaystyle s=(sin alpha +sin beta +sin gamma )/2} и диаметр описанной окружности {displaystyle D={tfrac {a}{sin alpha }}={tfrac {b}{sin beta }}={tfrac {c}{sin gamma }}}[4]:

S=D^{2}{sqrt {s(s-sin alpha )(s-sin beta )(s-sin gamma )}}.
  • Площадь вписанного в окружность четырёхугольника вычисляется по формуле Брахмагупты:
    S={sqrt {(p-a)(p-b)(p-c)(p-d)}},
где p={frac {a+b+c+d}{2}} — полупериметр четырёхугольника; в данном случае треугольник оказывается предельным случаем вписанного четырёхугольника при устремлении длины одной из сторон к нулю. Та же формула Брахмагупты через определитель[5]:

S={frac {1}{4}}{sqrt {-{begin{vmatrix}a&b&c&-d\b&a&-d&c\c&-d&a&b\-d&c&b&aend{vmatrix}}}}
где:

{displaystyle {begin{aligned}a&={sqrt {xYZ}}\b&={sqrt {yZX}}\c&={sqrt {zXY}}\d&={sqrt {xyz}}\X&=(w-U+v),(U+v+w)\x&=(U-v+w),(v-w+U)\Y&=(u-V+w),(V+w+u)\y&=(V-w+u),(w-u+V)\Z&=(v-W+u),(W+u+v)\z&=(W-u+v),(u-v+W)end{aligned}}}.
где theta _{s}={frac {theta _{a}+theta _{b}+theta _{c}}{2}} — полупериметр.

Примечания[править | править код]

  1. ↑ Weisstein, Eric W. Heron’s Formula. Архивная копия от 5 сентября 2015 на Wayback Machine From MathWorld–A Wolfram Web Resource.
  2. ↑ Benyi, Arpad, “A Heron-type formula for the triangle, « Mathematical Gazette» 87, July 2003, 324—326.
  3. ↑ Mitchell, Douglas W., “A Heron-type formula for the reciprocal area of a triangle, ” Mathematical Gazette 89, November 2005, 494.
  4. ↑ Mitchell, Douglas W., “A Heron-type area formula in terms of sines, ” Mathematical Gazette 93, March 2009, 108—109.
  5. ↑ Стариков В. Н. Заметки по геометрии// Научный поиск: гуманитарные и социально-экономические науки: сборник научных трудов. Выпуск 1/ Гл ред. Романова И .В Чебоксары: ЦДИП «INet», 2014. С. 37-39
  6. ↑ W. Kahan, «What has the Volume of a Tetrahedron to do with Computer Programming Languages?», [1] Архивная копия от 27 июня 2013 на Wayback Machine, pp. 16-17.
  7. ↑ Маркелов С. Формула для объёма тетраэдра// Математическое просвещение. Вып. 6. 2002. С. 132

Литература[править | править код]

  • § 258 в А. П. Киселёв, Геометрия по Киселёву, arΧiv:1806.06942 [math.HO].
  • Николаев Н. О площади треугольника // В.О.Ф.Э.М.. — 1890. — № 108. — С. 227—228.
  • Raifaizen, Claude H. A Simpler Proof of Heron’s Formula (англ.) // Mathematics Magazine : magazine. — 1971. — Vol. 44. — P. 27—28. — доказательство формулы Герона на основе теоремы Пифагора
Источник

Как найти периметр и площадь треугольника

Казалось бы, что может быть проще, чем вычисление площади и периметра треугольника – измерил стороны, поставил цифры в формулу – и все. Если вы так считаете, значит, забыли, что для этих целей существует не две простенькие формулы, а гораздо больше – для каждого вида треугольника – своя.

Как найти периметр и площадь треугольника

Инструкция

Периметр треугольника равняется сумме длин всех трех его сторон. Он вычисляется по формуле P=a+b+c, в которой a, b и c – это стороны фигуры.

Одна из самых известных формул нахождения площади треугольника – это формула Герона. Она выглядит следующим образом: S=√p(p-a)(p-b)(p-c). Символ p обозначает полупериметр, для его нахождения разделите периметр треугольника на два.

Чтобы найти площадь треугольника, если вам известна длина одной из сторон и длина высоты, опущенной на эту сторону, умножьте эти показатели, а результат разделите на два.

Если перед вами равносторонний треугольник, то чтобы узнать площадь, возведите длину его стороны во вторую степень. Затем умножьте полученную цифру на корень квадратный из трех. Данную цифру разделите на четыре.

Чтобы найти площадь прямоугольного треугольника, измерьте длины его катетов (сторон, прилежащих к прямому углу). Умножьте эти значения, а результат разделите на два.

Видео по теме

Обратите внимание

Формула Герона – универсальная для нахождения площади треугольника.

Полезный совет

Периметр треугольника находится суммой всех сторон. Для нахождения площади существует несколько разных формул.

Источники:

  • Как найти периметр и площадь треугольника
  • найти площадь треугольника 4 класс
  • Периметр равностороннего треугольника равен 18 900 мм

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

ТреугольникПериметром треугольника, как в прочем и любой фигуры, называется сумма длин всех сторон. Довольно часто это значение помогает найти площадь или используется для расчета других параметров фигуры.
Формула периметра треугольника выглядит так:

P=a+b+c

Калькулятор нахождения периметра треугольника

Сторона a= Сторона b= Сторона c=
Ответ: Периметр треугольника = 12.000

Иконка карандаша 24x24 Пример расчета периметра треугольника. Пусть дан треугольник со сторонами a = 4см, b = 6 см, c = 7 см. подставим данные в формулу: P=4+6+7=17см

Формула расчета периметра равнобедренного треугольника будет выглядеть так:

P=2a+b

Формула расчета периметра равностороннего треугольника:

P=3a

Иконка карандаша 24x24Пример расчета периметра равностороннего треугольника. Когда все стороны фигуры равны, то их можно просто умножить на три. Допустим, дан правильный треугольник со стороной 5 см в таком случае: P=3*5=15 см

В общем, когда все стороны даны, найти периметр довольно просто. В остальных же ситуациях требуется найти размер недостающей стороны. В прямоугольном треугольнике можно найти третью сторону по теореме Пифагора. К примеру, если известны длины катетов, то можно найти гипотенузу по формуле: c=sqrt{a^2+b^2}

Иконка карандаша 24x24Рассмотрим пример расчета периметра равнобедренного треугольника при условии, что мы знаем длину катетов в прямоугольном равнобедренном треугольнике.
Дан треугольник с катетами a=b=5 см. Найти периметр. Для начала найдем недостающую сторону с. c=sqrt{5^2+5^2}=sqrt{25+25}=sqrt{50}=7см
Теперь посчитаем периметр: P=5+5+7=17см
Периметр прямоугольного равнобедренного треугольника будет равен 17 см.

В случае, когда известна гипотенуза и длина одного катета, можно найти недостающий по формуле: a=sqrt{c^2-b^2}
Если в прямом треугольнике известна гипотенуза и один из острых углов, то недостающая сторона находится по формуле:

  • a=c*sin{alpha}
  • b=c*cos{alpha}

    • Если эти выражения подставить в формулу периметра, можно получить:

    P=a+b+c=c*sin{alpha}+ c*cos{alpha}+c=c*(sin{alpha}+cos{alpha}+1)

    Иконка карандаша 24x24Задача: Дан прямоугольный треугольник с гипотенузой с = 7 см и острым углом α = 30°. Найти периметр треугольника. Подставляем значения в формулу.
    P=7({1/2}+{sqrt{3}}/2+1)=7({1+1,7}/2+1)=16,45см
    Периметр треугольника равен 16,45 см

    Зная одну сторону и противолежащий ей катет можно вычислить две недостающие.

    Иконка карандаша 24x24К примеру, дан треугольник, в котором сторона a = 5 см, а противолежащий ей угол α =45°. Тогда сторону b можно найти через формулу:b=a/{tan{alpha}}
    Сторону с найдем так: c=a/{sin{alpha}}
    Периметр, с применением таких формул, будет рассчитываться следующим образом: P=a+b+c=a+a/{tan{alpha}} +a/{sin{alpha}} =a(1+1/{tan{alpha}} +1/{sin{alpha}})
    Теперь произведем расчеты по уже известной формуле: P=5(1+1/1+1/0,7)=5*3,4=17см

Источник

Треугольник — это элементарная геометрическая фигура, содержащая минимально возможное количество составляющих — три.

Точки соприкосновения сторон являются вершинами его углов, обозначаются заглавными латинскими символами A; B и C. Отрезки между вершинами являются сторонами или гранями треугольника и обозначаются названиями этих вершин: AB; BC; CA или прописной буквой противолежащего угла (вершины): AB=c; BC=a; CA=b.

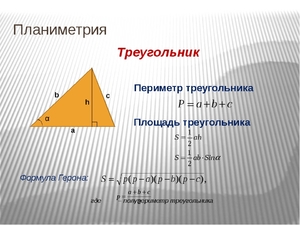
Периметр равен длине всех сторон фигуры, у треугольника он равен сумме трех сторон:

P=a+b+c.

Высота треугольника — это перпендикуляр от прямой, на которой лежит основание, до одноименной вершины, обозначается h.

Площадь составляет величину поверхности, заключенной внутри фигуры, обозначается S. Произведение основания на высоту дает значение площади. Ее можно определить и по формуле Герона:

  1. S=√(p·(p—a)·(p—b)·(p—c));
  2. p=½P.

Из этого видео вы узнаете, как найти площадь треугольника.

Классификация треугольников

Треугольник состоит из сторон и углов, сумма его углов всегда равна 180 градусов: A+B+C=180°.

  1. Равноугольный: все вершины равны 60°, будет и равносторонним.
  2. Равнобедренный: при равенстве двух граней углы на основании равны.
  3. Разноугольный: все вершины разные, ребра у него тоже разные.
  4. Прямоугольный: один угол равен 90°, примыкающие грани называются катеты, противолежащая — гипотенуза. Бывает равнобедренным (катеты равны) или разноугольным (катеты разные).
  5. Тупоугольный: один угол больше 90°. Может быть равнобедренным или разноугольным.

Как находить периметр треугольника

Описание

Чтобы описать любой треугольник, достаточно указать:

  1. Одну сторону и прилегающие к ней углы.
  2. Две стороны и угол между ними.
  3. Три стороны.

Данных из любого пункта достаточно для построения заданной фигуры и вычисления всех ее параметров, используя теорему косинусов:

c*c=a*a+b*b—2*a*b*cosC.

Подставляя известные значения, получим уравнение, решив которое узнаем неизвестные величины.

Cos90°=0, поэтому для прямоугольного треугольника c*c=a*a+b*b, где a и b — катеты, c — гипотенуза, сторона, лежащая напротив прямого угла.

Как найти периметр треугольника по формуле

Примеры

Известно, что одна грань равна 9 см и прилегающие углы по 60 градусов. Тогда из того, что сумма углов всегда равна 180°, получаем: 180=60+60+x; x=180—120=60. Все три вершины по 60°, значит, все стороны равны. Периметр составляет P=9+9+9=27 см, полупериметр p=13,5 см. Чтобы найти высоту, нужно опустить перпендикуляр из вершины на основание, получим прямоугольный треугольник с гипотенузой 9 см, катетом 4,5 см и катетом неизвестной длины, равным искомой высоте: 9*9—4,5*4,5=60,75=h2.

Высота равна корню квадратному из 60,75 или 7,79422863406 см. Умножаем основание на высоту, делим пополам и получаем площадь: 7,79422863406*9/2=35,074028853 см2. Если находить площадь по формуле Герона через полупериметр и ребра, ответ будет одинаковый:

S=√(13,5·(13,5—9)·(13,5—9)·(13,5—9))=35,074028853 см2.

Следующий пример с разносторонним треугольником. Дано: AB=12 см, BC=10 см, CA=8 см. Требуется найти периметр и площадь фигуры. P=a+b+c=BC+CA+AB=10 см+8 см+12 см=30 см. Площадь находим по формуле Герона, подставляя в нее уже известные значения, учитывая, что p=0,5Р; p=15 см. S=√(p·(p—a)·(p—b)·(p—c))=√(15·(15—10)·(15—8)·(15—12))=√15·5·7·3=√1575=39,686269666 см2.

Рассмотрим пример, когда известны два катета прямоугольного треугольника. Допустим, они имеют значения два и четыре метра. Тогда гипотенуза будет равна корню квадратному из суммы квадратов катетов √22+42=4,472135955 м. Периметр 2+4+4,472135955=10,472135955. Площадь равна половине произведения катетов S=2·4=8м2.

Способы нахождения периметра треугольника

Когда известны две стороны и угол между ними, остается найти только третью сторону по теореме косинусов. Пусть известные стороны составляют значения 16 и 28 метров, а угол между ними будет в 60 градусов, тогда третья сторона будет равна корню квадратному из этого выражения 162+282 — 2·16·28·0,5, что составит значение в 24,3310501212 м. Периметр равен 16+28+24,3310501212=68,3310501212≈68,33 м. Полупериметр будет 34,165 м. Подставляя полученные значения в формулу Герона, найдем площадь S=√(34,165·(34,165—16)·(34,165—28)·(34,165—24,33))=193,982314238 м2.

Если известно три параметра любого треугольника — два угла и сторона или две стороны и угол между ними, то ничего особенно сложного в нахождении неизвестных параметров треугольника — периметра, площади или высоты — нет. Нужно только внимательно производить простые вычисления. Иногда можно проявить и смекалку, разбив фигуру на несколько более простых в вычислении, например, прямоугольных треугольников. В каждом конкретном случае все зависит от исходных данных. Все формулы и вычисления, приведенные выше, верны для плоских фигур; для расположенных на сферической поверхности ход вычислений будет иным.

Видео

Это видео поможет вам закрепить полученные знания.

Источник

Добавить комментарий