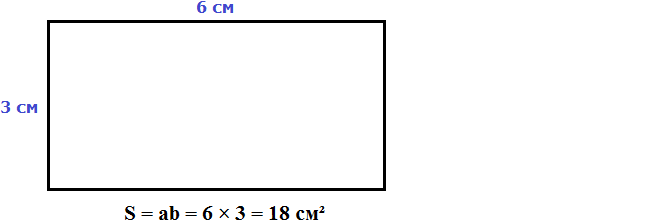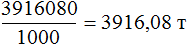Как найти периметр порядок действий - Сайт, где вы сможете решить свои вопросы

Запомните!

Периметр — это сумма длин всех сторон многоугольника.

Иногда для вычисления периметра геометрических фигур используются специальные формулы,
в которых периметр обозначается заглавной латинской буквой «P».

Периметр измеряется в единицах длины: мм, см, м, км и т.д.

При нахождении периметра мы рекомендуем писать название фигуры маленькими
буквами под знаком «P», чтобы не забывать чей периметр вы находите.

Запомните!

Периметр прямоугольника — это сумма длины и ширины, умноженная на «2».

P = (a + b) · 2

,
где «a» — длина прямоугольника, «b» — ширина прямоугольника.

Стороны прямоугольника, которые лежат друг против друга (противолежащие), мы
называем длиной и шириной.

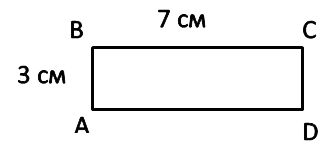
AB = 3 см, BC = 7 см

P_ABCD = (AB + BC) · 2
P_ABCD = (7 + 3) · 2 = 10 · 2 = 20 (см)

Запомните!

Периметр квадрата — это длина стороны квадрата, умноженная на «4».

P = a · 4

, где a — длина стороны квадрата.

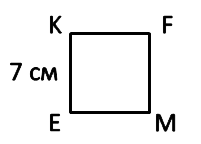
KE = 7 см

P_EKFM = 4 · KE
P_EKFM = 4 · 7 = 28 (см)

Как найти периметр многоугольника

Периметр любого многоугольника (в том числе и периметр треугольника)
рассчитывается по определению периметра.
Для этого надо просто сложить длины всех сторон многоугольника.

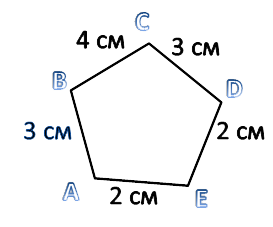
P_ABCDE = AB + BC + CD + DE + EA = 3 + 4 + 3 + 2 + 2 = 14 (см)

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

20 апреля 2017 в 17:19

Надежда Григоренко
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Надежда Григоренко
Профиль
Благодарили: 0

Сообщений: 1

длина прямоугольника 720м а ширина 18м меньше.найти ширину прямоугольника и его периметр

0
Спасибо thanks
Ответить

26 апреля 2017 в 20:06
Ответ для Надежда Григоренко

Ярослав Мудрый
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Ярослав Мудрый
Профиль
Благодарили: 0

Сообщений: 1

Нужно из 720 вычесть 18, а потом 720 · 2 + 702 · 2

0
Спасибо thanks
Ответить

17 мая 2017 в 22:22
Ответ для Надежда Григоренко

София Нгуен
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
София Нгуен
Профиль
Благодарили: 0

Сообщений: 2

720-18=702-ширина
Р=2(720+702)=2844

0
Спасибо thanks
Ответить

5 февраля 2017 в 12:17

Лев Дубров
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Лев Дубров
Профиль
Благодарили: 0

Сообщений: 1

на сколько изменится периметр прямоугольника если его длину увелисчить на 5.1/6 сантиметров, а ширину уменьшить на 1.1/2 сантиметров?

0
Спасибо thanks
Ответить

11 февраля 2017 в 13:46
Ответ для Лев Дубров

Алексей Карапов
(^-^)
Профиль
Благодарили: 0

Сообщений: 9

(^-^)
Алексей Карапов
Профиль
Благодарили: 0

Сообщений: 9

Формула прямоугольника после изменений
В которой
Р -Периметр
Р + (5.1/6 + 5.1/6) + (1.1/2 + 1.1/2)
Разкажу более подробней
Р + 10.2/6 +3 = Р + 13Целых и 2/6
ИЛИ
Периметр + сума в первых скобках + сума во вторых скобках

0
Спасибо thanks
Ответить

19 января 2017 в 18:22

София Желнаркевич
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
София Желнаркевич
Профиль
Благодарили: 0

Сообщений: 1

Периметр равнобедренного треугольника равен 15 см 8 мм.Основание треугольника 7 см 8 мм. Найдите боковые стороны треугольника.

0
Спасибо thanks
Ответить

20 февраля 2017 в 17:43
Ответ для София Желнаркевич

Алексей Карапов
(^-^)
Профиль
Благодарили: 0

Сообщений: 9

(^-^)
Алексей Карапов
Профиль
Благодарили: 0

Сообщений: 9

РЕШЕНИЕ: 15см8мм ? 7см8мм=8см8мм-2 боковые стороны;
8см8мм :2=4см4мм-1 боковая сторона

0
Спасибо thanks
Ответить

13 декабря 2016 в 19:36

Марина Ребрикова
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Марина Ребрикова
Профиль
Благодарили: 0

Сообщений: 1

стороны прямоугольника равны 12 см и 25 см, Вычислите его: а) периметр б) площадь

0
Спасибо thanks
Ответить

14 декабря 2016 в 16:37
Ответ для Марина Ребрикова

Руслан Потапов
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Руслан Потапов
Профиль
Благодарили: 0

Сообщений: 2

периметр р=2(а+в)=2(12+25)=74
площадь s=ав=300

0
Спасибо thanks
Ответить

20 декабря 2016 в 22:45
Ответ для Марина Ребрикова

Сарра Черенкова
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Сарра Черенкова
Профиль
Благодарили: 0

Сообщений: 1

Периметр находится так, нужно сложить сторону А и сторону В и умножить их на 2. Это, (12+25) · 2= 37 · 2=74 см. Площадь находится умножением стороны А на В. 12 · 25=300 см.

0
Спасибо thanks
Ответить

21 ноября 2016 в 20:55

Никита Зимоха
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Никита Зимоха
Профиль
Благодарили: 0

Сообщений: 1

длина прямоугольника в 4 раза больше ширины нйдите стороны прямоугольника, если уго периметр равен 130 дм.

0
Спасибо thanks
Ответить

23 ноября 2016 в 8:48
Ответ для Никита Зимоха

Владимир Баженов
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Владимир Баженов
Профиль
Благодарили: 0

Сообщений: 1

привет Никита .
4х+1х+4х+1х=130
10х=130
х=13 -длина маленькой стороны
4х=4*13=52 -длина большой стороны

Никита мне нужна твоя помощ. Напиши мне на почту hihkore2@yandex.ru

0
Спасибо thanks
Ответить

9 апреля 2016 в 17:37

Матвей Гамзиков
(^-^)
Профиль
Благодарили: 0

Сообщений: 3

(^-^)
Матвей Гамзиков
Профиль
Благодарили: 0

Сообщений: 3

Учебник геометрии 7 класс (Александров Вернер…) задача 7.35 Периметр прямоугольника равен 1. Найти стороны прямоугольника если: а)одна сторона больше другой в 2 раза, б) одна сторона больше другой на 0,1 в) одна сторона составляет 25% от другой. Вопросов по решению а и в нет. Выражаем одну сторону через другую составляем уравнение вычисления периметра и готово. Тогда как в варианте б не корректно поставлено условие, которое допускает два решения. По логике решения а и в X-одна сторона вторая равна X+0.1X=1.1X В ответе стороны равны 10/42 и 11/42. Сумма всех торон дает единицу. Но учитель утверждает что формула вычисления выглядит так 2X+2(X+0.1)=1 Т.е. согласно этого решения одна сторона больше другой на 0,1 периметра. но этого в условии не указано. Еще одно утверждение учителя что сторона больше другой на 0,1 единичного отрезка тоже никак не отражено в условии. Решение этого уравнения дает размеры сторон 2/10 и 3/10 сумма тоже равна 1 Ответ в учебнике именно этот. Так где-же логика которая от математики не должна отходить ни на шаг? Может я чего-то не понимаю? <col />

0
Спасибо thanks
Ответить

10 апреля 2016 в 9:26
Ответ для Матвей Гамзиков

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Большое спасибо, за попытку разобраться-это стоит многого! Кажется вопрос во внимательности. Если процитировать задачу, то пункт б) звучит именно так: «б) одна сторона больше другой на 0,1». И дальше вы сами же себе противоречите, говоря, что этого нет в задаче =).

Утверждение учителя, относительно формулы-абсолютно верное. Х-одна сторона. Вторая на 0,1 больше, следовательно Х+0,1. В прямоугольнике по две стороны каждой длины, а значит и периметр вычисляем умножив каждую на 2. 2Х+2(Х+0,1). По условию задачи, периметр равен 1. Составляем и решаем. 2/10 и 3/10 — ответ абсолютно верный. Есть второй момент, который может Вам помочь: Вы написали:«По логике решения а и в X-одна сторона вторая равна X+0.1X=1.1X ». В этом выражении присутствует ошибка. Если перевести его в текст, то условие задачи было бы: «Одна сторона больше другой в 0,1 раз». «В» — это умножение, а «На»-это сложение. Вот и получается, что учитель дал вам совершенно правильное уравнение для периметра. Удачи, надеюсь не сильно запутал!

0
Спасибо thanks
Ответить

10 апреля 2016 в 10:23
Ответ для Матвей Гамзиков

Матвей Гамзиков
(^-^)
Профиль
Благодарили: 0

Сообщений: 3

(^-^)
Матвей Гамзиков
Профиль
Благодарили: 0

Сообщений: 3

Спасибо за ответ. Тогда объясните с этой же позиции Одна сторона больше другой в 2раза.
Т.е. одна =Х, другая Х*2=2Х
одна сторона больше другой в 0,1
одна=Х, другая Х*0,1= 0,1Х т.е полусчается противоречие -сторона в еденицах измерения меньше первой. Для того что-бы на писать «в» нужно указать что одна сторона больше другой «в 1.1 раза
Поэтому в условии и сказано чтобольше на 0,1 только не указано от чего.
0,1 стороны прямоугольника или 0,1 периметра. Я еще раз настаиваю на не корректной постановки задачи. если задачу с этим условием незначительно изменить, то она получает не 2 а 3 решения и все три правильные.
Если периметр будет равен 3 а остальные условия останутся прежними: в случае относительно сторон одна сторона = , вторая = , периметр=3,
вслучае относительно периметра одна сторона=0,6, вторая=0,9, периметр= 3,
вслучае решения по учебнику одна сторона= , вторая = , периметр=3,
Математика наука точная постановки задач в математике должны быть точными и корректными, не допускающими двойного толкования. Тогда у нас небудуть падать спутники и сталкиваться в лобовую поезда. Внимательно и с удовольствием выслушаю все доказательства того, что вариант решения по учебнику единственно правильный.
Попробуйте решить простую задачу: одна сторона прямоугольника= 1фут другая на 0,1 больше напишите размеры сторон в сантиметрах

0
Спасибо thanks
Ответить

10 апреля 2016 в 17:25
Ответ для Матвей Гамзиков

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

И снова добрый день. Вот здесь и есть недопонимание: «Поэтому в условии и сказано чтобольше на 0,1 только не указано от чего.
0,1 стороны прямоугольника или 0,1 периметра. Я еще раз настаиваю на не корректной постановки задачи. если задачу с этим условием незначительно изменить, то она получает не 2 а 3 решения и все три правильные.»

Больше на 0,1. Значит, что больше на 0,1 условную единицу. Задайте себе вопрос, почему Вас не смущает в условии: «Периметр равен 1»? Не 1 см, не 1фут. а просто 1. Ровно из тех же соображений, написано больше на 0,1.

По мимо того, что математика наука точная, она учит ещё и абстрактному мышлению и принятию некоторых условий. Если не указана единица измерения, то берётся некоторая абстрактная условная единица, просто об этом не пишут.

А Ваша задача решается предельно просто:

Т.к. размер одной стороны 1 фут, а вторая больше неё на 0,1 ПРЕДПОЛОЖИМ, что больше она на 0,1 фут. Следовательно размер второй стороны 1,1 фут.

1фут=30,48 см.
1,1фут=33,528см.

Если же ПРЕДПОЛОЖИТЬ, что больше на 0,1 см, то сначала выражаем первую сторону в см, а потом прибавляем 0,1см.
1фут=30,48см
30,48см+0,1см=30,58см.

Ни один преподаватель после такого объяснения и описания вам не скажет ничего осуждающего, а только похвалит.

Стоит отметить, что в исходной задче не указаны единицы измерения, а вы их сами взяли и смешали, так что сравнение некорректное.

И ещё маленькое уточнение: В этом мире, к сожалению, всего знать невозможно. Если Вы считаете, что в учебнике ошибка-напишите в редакцию, подробно опишите проблему и Вам наверняка ответят. благо современные средства связи позволяют.

Боритесь за свою правоту! Главное-умейте признавать ошибки! =)

Всего доброго! =)

0
Спасибо thanks
Ответить

10 апреля 2016 в 18:22
Ответ для Матвей Гамзиков

Матвей Гамзиков
(^-^)
Профиль
Благодарили: 0

Сообщений: 3

(^-^)
Матвей Гамзиков
Профиль
Благодарили: 0

Сообщений: 3

Приятно получить исчерпывающий ответ. Я поэтому и задал вопрос об 1футе. Стоит ввести небольшое уточнение как задача теряет единственность решения. Это уже ближе вероятному решению А если взадаче указать 0,1 от периметра то единственностьрешения не измениться при любых вводных условиях. Приятно было общаться.

0
Спасибо thanks
Ответить

14 июня 2016 в 19:50
Ответ для Матвей Гамзиков

Евгений Фёдоров
(^-^)
Профиль
Благодарили: 0

Сообщений: 60

(^-^)
Евгений Фёдоров
Профиль
Благодарили: 0

Сообщений: 60

Не морочь людям голову.
Задача ясно и однозначно поставлена.
В учебнике ответ и .

0
Спасибо thanks
Ответить

3 апреля 2016 в 12:15

Димка Шаменков
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Димка Шаменков
Профиль
Благодарили: 0

Сообщений: 1

? 1/12 части квадрата 3см? Найти ? всего квадрата

0
Спасибо thanks
Ответить

4 апреля 2016 в 8:15
Ответ для Димка Шаменков

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Если площадь части квадрата 3, то площадь всего квадрата в 12 раз больше. Т.е. 12 · 3= 36.
36см²-площадь всего квадрата.

0
Спасибо thanks
Ответить

17 января 2016 в 15:47

Сергей Малярчук
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Сергей Малярчук
Профиль
Благодарили: 0

Сообщений: 1

периметр прямоугольника равен 36см. найдите площадь прямоугольника, если известно, что его стороны относятсякак: а1:5 б1:3 в1:2 г1:1.как меняется площадь прямоугольника от первого к последнему случаю? у какого прямоугольника площадь наибольшая?

0
Спасибо thanks
Ответить

19 сентября 2016 в 11:40
Ответ для Сергей Малярчук

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Периметр прямоугольника.
P=2(a+b)
Площадь прямоугольника.
S=a · b
a)36=2(x+5x)
36=12x
x=3
a=3
b=5 · 3=15
S=a · b =3 · 15=45
Далее логика аналогичная:
б)36=2(x+3x)
a=4,5
b=13,5
S=60,75
в)36=2(x+2x)
a=6
b=12
S=72
г)36=2(x+x)
a=12
b=12
S=144
Площадь прямоугольника увеличивается. Площадь прямоугольника г) — наибольшая. Прямоугольник г) также является квадратом. т.к. стороны равны.

0
Спасибо thanks
Ответить

12 января 2016 в 18:45

Артем Василенко
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Артем Василенко
Профиль
Благодарили: 0

Сообщений: 1

Знайди периметр трикутника зі сторонами 2 см 8мм, 3 см 4мм,1 см 7 мм.

0
Спасибо thanks
Ответить

12 января 2016 в 18:50
Ответ для Артем Василенко

Кирилл Нечаев
(^-^)
Профиль
Благодарили: 0

Сообщений: 3

(^-^)
Кирилл Нечаев
Профиль
Благодарили: 0

Сообщений: 3

0
Спасибо thanks
Ответить

12 января 2016 в 18:51
Ответ для Артем Василенко

Кирилл Нечаев
(^-^)
Профиль
Благодарили: 0

Сообщений: 3

(^-^)
Кирилл Нечаев
Профиль
Благодарили: 0

Сообщений: 3

34417

0
Спасибо thanks
Ответить

12 января 2016 в 18:52
Ответ для Артем Василенко

Кирилл Нечаев
(^-^)
Профиль
Благодарили: 0

Сообщений: 3

(^-^)
Кирилл Нечаев
Профиль
Благодарили: 0

Сообщений: 3

34417

0
Спасибо thanks
Ответить

19 сентября 2016 в 10:35
Ответ для Артем Василенко

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Чтобы найти периметр треугольника(если я правильно понял название фигуры) нужно сложить длины его сторон. Нужно учитывать, что в 1см=10мм. Переведём всё в мм и сложим. P=a+b+c=28+34+17=79мм=7см9мм.

0
Спасибо thanks
Ответить

11 ноября 2015 в 17:47

Дианочка Лазарева
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Дианочка Лазарева
Профиль
Благодарили: 0

Сообщений: 1

Длина прямоугольника в 8 раз больше ширины.найдите площадь и периметр прямоугольника, если ширина на 42 см меньше длины

0
Спасибо thanks
Ответить

16 сентября 2016 в 13:37
Ответ для Дианочка Лазарева

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Обозначим:
a-длина
b-шрина
Длина в 8 раз больше ширины: a=8b
Ширина на 42см меньше длины: a=b + 42
Вычислим отсюда b: b + 42=8b
7b=42
b=6 — ширина равна 6, тогда длина a=6 · 8 = 48.
Периметр прямоугольника P = 2a + 2b = 2 · 6 + 2 · 48 = 108
Площадь прямоугольника S = a · b = 2 · 48 = 96

0
Спасибо thanks
Ответить

23 октября 2015 в 10:20

Галина Тимичева
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Галина Тимичева
Профиль
Благодарили: 0

Сообщений: 2

периметр квадрата равен 12см. найдите сторону квадрата и начертите его.

0
Спасибо thanks
Ответить

23 октября 2015 в 10:23
Ответ для Галина Тимичева

Галина Тимичева
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Галина Тимичева
Профиль
Благодарили: 0

Сообщений: 2

периметр квадрата равен 12см. найдите сторону квадрата и начертите его.

0
Спасибо thanks
Ответить

23 октября 2015 в 17:59
Ответ для Галина Тимичева

Марина Реснянская
(^-^)
Профиль
Благодарили: 0

Сообщений: 4

(^-^)
Марина Реснянская
Профиль
Благодарили: 0

Сообщений: 4

И ТАК 12: 4 =3СМ СТОРОНА КВАДРАТА И ЧЕРЧИШЬ КВАДРАТ 3*3

0
Спасибо thanks
Ответить

23 октября 2015 в 18:00
Ответ для Галина Тимичева

Марина Реснянская
(^-^)
Профиль
Благодарили: 0

Сообщений: 4

(^-^)
Марина Реснянская
Профиль
Благодарили: 0

Сообщений: 4

И ТАК 12: 4 =3СМ СТОРОНА КВАДРАТА И ЧЕРЧИШЬ КВАДРАТ 3*3

0
Спасибо thanks
Ответить

23 октября 2015 в 21:21
Ответ для Галина Тимичева

Елизавета Яременко
(^-^)
Профиль
Благодарили: 0

Сообщений: 5

(^-^)
Елизавета Яременко
Профиль
Благодарили: 0

Сообщений: 5

Мне кажется, что:
1)12:4=3(см)-сторона квадрата.

0
Спасибо thanks
Ответить

27 октября 2015 в 15:27
Ответ для Галина Тимичева

Марина Доценко
(^-^)
Профиль
Благодарили: 0

Сообщений: 3

(^-^)
Марина Доценко
Профиль
Благодарили: 0

Сообщений: 3

1)12: 4=3(см)-сторона квадрата

0
Спасибо thanks
Ответить

9 ноября 2015 в 18:48
Ответ для Галина Тимичева

София Тышкевич
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
София Тышкевич
Профиль
Благодарили: 0

Сообщений: 2

согласна что тут непонятного

0
Спасибо thanks
Ответить

9 ноября 2015 в 18:49
Ответ для Галина Тимичева

София Тышкевич
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
София Тышкевич
Профиль
Благодарили: 0

Сообщений: 2

согласна что тут непонятного

0
Спасибо thanks
Ответить

14 ноября 2015 в 19:05
Ответ для Галина Тимичева

Максим Бычков
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Максим Бычков
Профиль
Благодарили: 0

Сообщений: 2

12: 4=3

0
Спасибо thanks
Ответить

22 октября 2015 в 15:34

Эльза Прокофьева
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Эльза Прокофьева
Профиль
Благодарили: 0

Сообщений: 1

Пожалуйста помогите с Домашним Заданием для 3 класса! cry Ширина прямоугольника 3 см, а длина в 4 раза больше. Найди периметр и площадь прямоугольника.

0
Спасибо thanks
Ответить

23 октября 2015 в 13:47
Ответ для Эльза Прокофьева

Елизавета Яременко
(^-^)
Профиль
Благодарили: 0

Сообщений: 5

(^-^)
Елизавета Яременко
Профиль
Благодарили: 0

Сообщений: 5

3 · 4 Это площадь3 + 4 + 3 + 4 Это периметр

0
Спасибо thanks
Ответить

23 октября 2015 в 13:48
Ответ для Эльза Прокофьева

Елизавета Яременко
(^-^)
Профиль
Благодарили: 0

Сообщений: 5

(^-^)
Елизавета Яременко
Профиль
Благодарили: 0

Сообщений: 5

Ну как?
я 5 класс
спрашивай если что

0
Спасибо thanks
Ответить

23 октября 2015 в 18:03
Ответ для Эльза Прокофьева

Марина Реснянская
(^-^)
Профиль
Благодарили: 0

Сообщений: 4

(^-^)
Марина Реснянская
Профиль
Благодарили: 0

Сообщений: 4

1)ДЛИНА=3 УМНОЖИТЬ НА 2 =6
р=2*6=12 СМ
2)24:3=4

0
Спасибо thanks
Ответить

23 октября 2015 в 18:03
Ответ для Эльза Прокофьева

Марина Реснянская
(^-^)
Профиль
Благодарили: 0

Сообщений: 4

(^-^)
Марина Реснянская
Профиль
Благодарили: 0

Сообщений: 4

НАЙДИ В ЯНДЕКСЕ.

0
Спасибо thanks
Ответить

26 октября 2015 в 11:59
Ответ для Эльза Прокофьева

Иван Мудрак
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Иван Мудрак
Профиль
Благодарили: 0

Сообщений: 1

я тож пятый класс

0
Спасибо thanks
Ответить

27 октября 2015 в 15:24
Ответ для Эльза Прокофьева

Марина Доценко
(^-^)
Профиль
Благодарили: 0

Сообщений: 3

(^-^)
Марина Доценко
Профиль
Благодарили: 0

Сообщений: 3

3*4=12cм — площадь
(3+4)*2=14см — периметр

0
Спасибо thanks
Ответить

27 октября 2015 в 15:25
Ответ для Эльза Прокофьева

Марина Доценко
(^-^)
Профиль
Благодарили: 0

Сообщений: 3

(^-^)
Марина Доценко
Профиль
Благодарили: 0

Сообщений: 3

Лиза я тоже в 5 классе

0
Спасибо thanks
Ответить

29 октября 2015 в 15:55
Ответ для Эльза Прокофьева

Марья Голдобина
(^-^)
Профиль
Благодарили: 0

Сообщений: 4

(^-^)
Марья Голдобина
Профиль
Благодарили: 0

Сообщений: 4

3 · 4=12-длина
12 · 3=36-S
12+3+36=51-P

точно не помню не судите строго

0
Спасибо thanks
Ответить

30 марта 2016 в 15:52
Ответ для Эльза Прокофьева

Галина Петухова
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Галина Петухова
Профиль
Благодарили: 0

Сообщений: 1

незнаю когда это было но девочке 2 поставели потому что:
3*4=12 это длина прямоугольника
(3+12)*2=30см а не 12 это p
3*12=36 кв см это S
всё!!!!!!!!!!!!

0
Спасибо thanks
Ответить

15 сентября 2016 в 10:46
Ответ для Эльза Прокофьева

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Вот это неразбериха! Хотя ответ правильный уже дан, может понятнее будет+приведу ссылки на объяснение на сайте.
1) найдём длину прямоугольника. Т.к. она в 4 раза больше ширины, значит нужно длину умножить на 4.
3 · 4 = 12 (см) — длина прямоугольника.
2) Периметр прямоугольника — сумма всех его сторон. У прямоугольника 2 длины и две ширины. Подробнее здесь.
P=2a+2b
P=2 · 3 + 2 · 12 = 6 + 24 = 30 (см) — периметр прямоугольника.
3) Площадь прямоугольника это произведение ширины на длину. Подробнее здесь.
S=a · b
S=3 · 12 = 36 (см²) — площадь прямоугольника.

Ответ: P=30см, S=36см²

0
Спасибо thanks
Ответить

16 сентября 2015 в 18:25

Света Шульга
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Света Шульга
Профиль
Благодарили: 0

Сообщений: 1

Из двух листов картона, имеющих форму квадрата, длина стороны которого 30 см, вырезали два круга. Найдите площадь обрезков картона, если 3,14

0
Спасибо thanks
Ответить

8 сентября 2016 в 16:24
Ответ для Света Шульга

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Т.к. мы имеем два одинаковых листа картона и два одинаковых круга, которые из них вырезают, то найдём площадь обрезков от одного и умножим на 2. ПРЕДПОЛОЖИМ, что круг вырезают максимально возможного радиуса. В таком случае, радиус круга равен половине длины стороны квадрата (лучший сопсоб это представить-вырезать из реальной бумаги.) Что такое обрезки? это то, что осталось, после вырезания круга, т.е. разница между площадью квадрата(листа картона) и площадью круга, который вырезают из этого листа.
Площадь квадрата S=a²
Площадь круга S=?r²=?()²=
Площадь обрезков S=a² ?

0
Спасибо thanks
Ответить

8 сентября 2016 в 16:29
Ответ для Света Шульга

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

S=900 ? =900 ? 3,14 · 225 = 193,5

Т.к. квадратов 2, то полученный результат умножаем на 2. 193,5 · 2 = 387
Ответ: Площадь обрезков равна 387 см²P.S. Данное решение будет верным, в случае нашего ПРЕДПОЛОЖЕНИЯ

0
Спасибо thanks
Ответить

4 сентября 2015 в 15:35

Игорь Винников
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Игорь Винников
Профиль
Благодарили: 0

Сообщений: 2

Периметр прямоугольника 36см, одна из сторон12см. Чему равны другие три стороны?

0
Спасибо thanks
Ответить

1 сентября 2016 в 10:15
Ответ для Игорь Винников

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Периметр это сумма длин сторон. В прямоугольнике противоположные стороны равны по длине. Предположим, что одна сторона равна a, а другая b.
Периметр прямоугольника вычисляется по формуле:
P=a+a+b+b=2a+2b. Допустим, что сторона a=12см. Подставим значения в формулу:
36 = 2 · 12 + 2 · b
2 · b = 36 ?2 · 12
2 · b = 12
b = 6
Произведем проверку, подставив значения в формулу перметра.
2 · 12 +2 · 6 = 24 + 12 = 36
Следовательно, ответ был получен верно.

Ответ: оставшиеся стороны прямоугольника равны 12см, 6см, 6см.

0
Спасибо thanks
Ответить

26 августа 2015 в 21:11

Таня Грига
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Таня Грига
Профиль
Благодарили: 0

Сообщений: 2

Петерсон. 5 класс 1 часть №102
Одна из сторон прямоугольника на 10 см меньше другой. Если меньшую сторону увеличить на 15 см, а большую увеличить на 20 см, то площадь прямоугольникаувеличиться в 5 раз. Чему равна ширина данного прямоугольника?

0
Спасибо thanks
Ответить

26 августа 2015 в 21:13
Ответ для Таня Грига

Таня Грига
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Таня Грига
Профиль
Благодарили: 0

Сообщений: 2

Какую из сторон брать за Х?

0
Спасибо thanks
Ответить

1 сентября 2016 в 9:41
Ответ для Таня Грига

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Не принципиален выбор стороны за X. Обозначим большую сторону за X, тогда другая сторона будет X-10, т.е. на 10 см меньше. Если обозначить за X меньшую сторону, то другая сторона будет X+10.

Рассмотрим первый вариант.
Одна сторона — X, другая сторона X-10.
Площадь прямоугольника равна произведению длины на ширину(a · b) или X · (X-10). Обозначим площадь за S.
Учитывая второе условие составим ещё одно уравнение:
(X +20) · (X ?10 + 15) = 5 · S
S =

Выразив S из каждого уравнения, приравняем их и вычислим значение X.
X · (X ?10) =
5 · X² ? 50 · X = X²+ 5 · X + 20 · X + 100
4 · x² ? 75 · x ? 100 = 0
Решим квадратное уравнение:
D = (-75)² ? 4 · 4 · (-100) = 5625 + 1600 = 7225

x₁=

= — 1,25
x₂ = = 20
Т.к. длина стороны не может быть выражена отрицательным значением, то остаётся только один ответ: 20. Следовательно длина прямоугольника равна 20, а ширина 20-10=10, а площадь соотвественно 20 · 10 = 200.

Проверим получившиеся значения, применив известное по задаче условие:

(20+20) · (10+15) = 40 · 25 = 1000
1000: 5 =200
Условие выполняется, а значит ответ подобран верно.
Ответ: ширина данного прямоугольника равна 10 см.

0
Спасибо thanks
Ответить

14 мая 2015 в 18:17

Настя Фадеева
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Настя Фадеева
Профиль
Благодарили: 0

Сообщений: 1

Сторона квадрата равна 14 мм. Чему равна его площадь

0
Спасибо thanks
Ответить

14 мая 2015 в 21:45
Ответ для Настя Фадеева

Ярик Кравченко
(^-^)
Профиль
Благодарили: 0

Сообщений: 3

(^-^)
Ярик Кравченко
Профиль
Благодарили: 0

Сообщений: 3

14мм *14мм= 196мм= 190,6 см

0
Спасибо thanks
Ответить

19 мая 2015 в 15:04
Ответ для Настя Фадеева

Мадина Зиямидинова
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Мадина Зиямидинова
Профиль
Благодарили: 0

Сообщений: 1

14 * 14*14*14 = 56

0
Спасибо thanks
Ответить

23 октября 2015 в 21:37
Ответ для Настя Фадеева

Елизавета Яременко
(^-^)
Профиль
Благодарили: 0

Сообщений: 5

(^-^)
Елизавета Яременко
Профиль
Благодарили: 0

Сообщений: 5

14-1сторона квадрата
всего их 4 поэтому умножаем на 4
1)14.4=56мм-4стороны квадрата)))))))

0
Спасибо thanks
Ответить

17 апреля 2016 в 16:22
Ответ для Настя Фадеева

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Площадь квадрата — это квадрат его стороны. А периметр квадрата, это сумма длин его сторон. Т.е. сторона умноженная на 4. Следовательно, ответ данный Яриком Кравченко-абсолютно верный, за исключением перевода в см: 14*14 = 196(мм) = 19,6 см.

Остальные ответы не верные даже в расчете.

0
Спасибо thanks
Ответить

21 апреля 2015 в 8:42

Надежда Григорьева
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Надежда Григорьева
Профиль
Благодарили: 0

Сообщений: 1

Длина прямоугольника 2,8 дм, а ширина в 4 раза меньше длины. Найдите длину стороны квадрата, площадь которого равна площади прямоугольника

0
Спасибо thanks
Ответить

14 апреля 2016 в 11:54
Ответ для Надежда Григорьева

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

1) Найдём ширину прямоугольника: 2,8/4=0,7.
2) Найдём площадь прямоугольника: S=a · b = 2,8 · 0,7 = 1,96
3) Площадь квадрата: S=a². Следовательно сторона: а=?S
a=?1,96=±1,4. Длина стороны не может быть отрицательной, а значит равна 1,4.
Ответ 1,4дм

0
Спасибо thanks
Ответить

Источник

Download Article

The perimeter is the length of an outline of a shape. The general way to find the perimeter of any shape is to add up the length of all its sides. For certain shapes, such as rectangles and circles, there are specific formulas you can use to simplify the process. In other instances, you might be missing one or more of the side lengths, but are given other information. In cases like this, you must complete extra steps to find the missing side length before you can calculate the perimeter.

1
Perimeter is defined as the length surrounding a given area. Imagine you had a fence that runs around your entire property. In order to find the total length of the fence, you’d need to calculate the perimeter. Measuring the entire fence by hand is one way to do it, but an easier way is to use the perimeter formula.^[1]
- You might not be given the length of all 4 sides, which is another reason why you’d need to use an equation to find the perimeter instead of just addition.
2
Circumference is the perimeter of a circle. Since a circle doesn’t have any straight lines, the method for figuring out its perimeter is a little bit different. It involves using Pi and the radius or diameter of the entire shape.^[2]
- You can’t find the perimeter of a circle just by measuring it; you have to use the circumference equation.
Advertisement
3
Express the perimeter in distance units. These are feet, inches, centimeters, miles, etc. Since you’re measuring the length of something, you always have to use real-world distance units when you get your answer.^[3]
- You’ll have to make sure all your units are the same before you do your equation, too. This might mean changing feet to inches, miles to feet, or anything in between.
4
Use an online calculator to check your answer. Although you might have to show your work on your homework or assignment, you can always use an online calculator to double check that you’re doing it right. Search for the shape you’re working on + perimeter in a web browser to find free online calculators that you can use.^[4]
- Make sure you’re using a calculator for your specific shape.

1
Set up the formula for the perimeter of a rectangle. The formula is , where equals the perimeter of the rectangle, equals the width of the rectangle, and equals the height of the triangle. If you don’t know the length of the width and height of the rectangle, you cannot use this formula.
- You can also use the formula , where each variable is equal to the length of one side of the rectangle. A variable is any number in your equation that you use, signified by letters (a, b, c, d).
- If you don’t know the height and width of your shape, you can plug in the information you do know, like the area, the length of one side, or the length of the diagonal.
2
Plug the width and height into the formula. It doesn’t matter which measurement you use for the width and which you use for the height since the width and height are two adjacent sides. If the rectangle is not a square, these side lengths must be different.
- For example, if a rectangle has a width of 5 cm and a height of 10 cm, your formula will look like this: .
3

Add the length and width, and multiply by 2. Make sure you follow the order of operations and complete the calculation in parentheses before multiplying. The resulting value will give you the perimeter of your rectangle.^[5]
4
5

Find the perimeter given other information. Often you will not be given the length of all sides, or even the length of any side. It still may be possible to find the perimeter of a rectangle.^[7]

1
Set up the formula for finding the perimeter of a triangle. The formula is , where the variables equal the three sides of the triangle. This formula is the same whether or not the triangle is right. You must have all side lengths to use this formula. If you know that you have an equilateral triangle, you only need one side length, since an equilateral triangle has three equal sides.^[13]
- For example, if a triangle has sides that are 5, 7, and 12 cm in length, you simply add up all the side lengths to find the perimeter: . So, the perimeter of the triangle is 24 cm.
2
3
Find the perimeter of an isosceles triangle with a missing side length. An isosceles triangle is when the height, or the altitude, bisects the base. If you know the height and base of the triangle, you can use the Pythagorean theorem to find the missing side lengths.^[15]
- For example, if an isosceles triangle has a height of 10 cm and a base of 6 cm, you can think of the height creating two right triangles. Since the height bisects the base, one side length of the right triangle will be 3 cm. The other side length will be equal to the height: 10 cm. The missing side length is the hypotenuse.
- Set up the Pythagorean formula, plugging in the side lengths: $10^{{2}}+3^{{2}}=c^{{2}}$ .
- Make the necessary calculations to find the missing side length:
  $100+9=c^{{2}}$
  $109=c^{{2}}$
  ${sqrt {109}}={sqrt {c^{{2}}}}$
  .
- An isosceles triangle has 2 equal sides. So, the perimeter of the triangle is equal to , where equals the length of one side, and equals the base. So, if you know the length of the base and one side, you can find the perimeter of an isosceles triangle: . So, the perimeter of the triangle is 26.88 cm.

1

Find the length of one side. A regular polygon is a polygon that is equiangular and equilateral. You can find the length of one side if you know the length of the polygon’s apothem or radius. The apothem is the distance between the center of the polygon to the midpoint of any side, and the radius is the distance between the center of the polygon and any vertex.^[16]
2

Set up the formula for the perimeter of a regular polygon. The formula is , where is the number of sides the polygon has, and is the length of one side.^[19]
3

1
Measure the “sides” of your ellipse. An ellipse is an oval-shaped circle, so it doesn’t have any straight lines. To find the perimeter, you need to know the circumference of both the height and the width, or variables a and b. If you don’t know this information already, you can measure your ellipse on your own.^[21]
- Normally, variable a goes from left to right on the major axis, and variable b goes up and down on the minor axis.
2
Plug the information into an equation. There are actually a few different equations that you can use to find the perimeter of an ellipse, and they all may give you a slightly different answer. The easiest formula to use is: ${displaystyle p=2pi {sqrt {(a^{2}+b^{2})/2}}.}$ ^[22]
- This will give you an answer within 5% of the true perimeter of the ellipse.
- For example, if variable a is 3 and variable b is 2, your equation would look like this: ${displaystyle p=2pi {sqrt {(3^{2}+2^{2})/2}}.}$
3

Solve the equation. Now you can use your inputted variables to find the perimeter of the ellipse. Remember that this is an approximate answer, not an exact one.^[23]

1
Find the length of the arc. A sector is a triangular slice taken from a whole circle (it looks like a piece of pizza). To start the equation, you need to find the length, or variable l, of the arc itself.^[24]
- If you aren’t given that information, you can solve for l with this equation: .
2
Plug the variables into the equation. To find the perimeter of a sector, plug your numbers into this equation: , where “2r” is 2 times the radius and “θ” is the angle of the sector. Once you’ve done that, you can solve for the perimeter.^[25]
- For example, .
3
Solve the equation. Once you’ve plugged in your variables, you can use the order of operations to solve for the perimeter. This is an exact number, so use the equal sign for your answer.^[26]
- .

1

Find the number of sides and the length of one side. A pentagon always has 5 sides, so you’ll always be able to plug 5 into your equation. Then, all you need to find out is the length of one side to plug in for the variable.^[27]
2
Plug the variables into the equation. The formula to find the perimeter of a pentagon is . The variable “s” stands for the length of 1 side.^[28]
- For example, your equation might look like this: .
3
Solve for the perimeter. Once you’ve got your equation, you can use the formula to figure out the answer. Check your answer on a calculator to make sure it’s right.^[29]
- For example, .

1
Find the length of all 4 sides. A quadrilateral looks like a rectangle with uneven sides. If you know all 4 sides of the quadrilateral, you can find the perimeter by adding them all up.^[30]
- If you don’t know the length of all 4 sides, you can use the information you do have to solve for variable x.
2
Plug the side lengths into your equation. To find the perimeter of a quadrilateral, you just need to add up the side lengths. The formula is .^[31]
- For example, .
3
Add up the lengths to find the perimeter. Once you know all 4 side lengths, just add them up. Don’t forget to put your units on the end of your answer.^[32]
- For example, .

Add New Question

Question

If given area and length of a rectangle, how do I find the perimeter?

Divide the area by the length, giving you the width. Add twice the width to twice the length.
Question

What’s the perimeter of a triangle that has sides of 2/3, 2/5 and 2/3?

Add the three sides together: 2/3 + 2/5 + 2/3 = 10/15 + 6/15 + 10/15 = 26/15 = 1 11/15.
Question

The perimeter of a rectangle is 64 feet. Length is 7 feet less than 2 times the width. What are the dimensions of the rectangle?

Let x = the width. Then the length is 2x – 7. The perimeter is twice the width plus twice the length: 64 = (2x) + 2(2x – 7) = (2x) + (4x – 14) = 6x – 14. So 64 = 6x – 14, and 78 = 6x. Then x = 13 ft, and the length is (2)(13) – 7 = 26 – 7 = 19 ft. To check: (2)(13) + (2)(19) = 26 + 38 = 64.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

To find the perimeter of a trapezoid when you are missing side lengths, in general you want to divide the trapezoid into two right triangles and one rectangle. From there you can use the properties of right triangles and rectangles to find the missing side lengths.
To find the perimeter of a rhombus when you are missing side lengths, in general you want to use the diagonal(s) of the rhombus to divide the shape into several right triangles. Then you can use the Pythagorean theorem or trigonometry to find the missing side lengths.

Thanks for submitting a tip for review!

Video

References

About This Article

Article SummaryX

The right way to find perimeter depends on the shape you’re working with. For rectangles, use the formula p = 2 (w + h), where w is the width of the rectangle and h is the height. To find the perimeter of a square, use the formula p = 4x, where x is the length of 1 side of the square. If you need to find the perimeter of a triangle, use the formula p = a + b + c, where a, b, and c are the lengths of the 3 sides of the triangle. Finally, to find the perimeter of a circle, use the formula c = π (d), where c is the perimeter and d is the diameter. If you want to learn how to find the perimeter of any regular polygon, keep reading the article!

Did this summary help you?

Thanks to all authors for creating a page that has been read 138,911 times.

Did this article help you?

Источник

Данный материал содержит геометрические фигуры с измерениями. Приведённые измерения являются приблизительными и могут не совпадать с измерениями в реальной жизни.

Периметр геометрической фигуры

Периметр геометрической фигуры — это сумма всех её сторон. Чтобы вычислить периметр, нужно измерить каждую сторону и сложить результаты измерений.

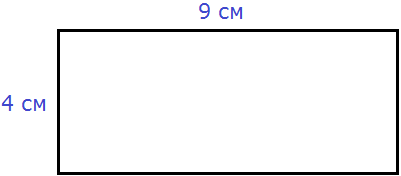
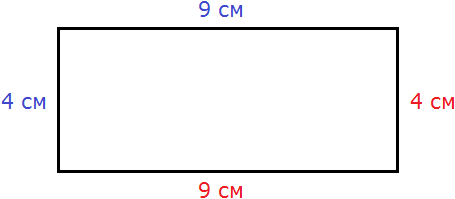
Вычислим периметр следующей фигуры:

Это прямоугольник. Детальнее мы поговорим об этой фигуре позже. Сейчас просто вычислим периметр этого прямоугольника. Длина его равна 9 см, а ширина 4 см.

У прямоугольника противоположные стороны равны. Это видно на рисунке. Если длина равна 9 см, а ширина равна 4 см, то противоположные стороны будут равны 9 см и 4 см соответственно:

Найдём периметр. Для этого сложим все стороны. Складывать их можно в любом порядке, поскольку от перестановки мест слагаемых сумма не меняется. Периметр часто обозначается заглавной латинской буквой P (англ. perimeters). Тогда получим:

P = 9 см + 4 см + 9 см + 4 см = 26 см.

Поскольку у прямоугольника противоположные стороны равны, нахождение периметра записывают короче — складывают длину и ширину, и умножают её на 2, что будет означать «повторить длину и ширину два раза»

P = 2 × (9 + 4) = 18 + 8 = 26 см.

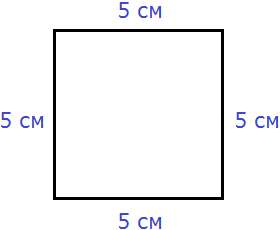
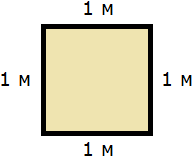
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, найдём периметр квадрата со стороной 5 см. Фразу «со стороной 5 см» нужно понимать как «длина каждой стороны квадрата равна 5 см»

Чтобы вычислить периметр, сложим все стороны:

P = 5 см + 5 см + 5 см + 5 см = 20 см

Но поскольку все стороны равны, вычисление периметра можно записать в виде произведения. Сторона квадрата равна 5 см, и таких сторон 4. Тогда эту сторону, равную 5 см нужно повторить 4 раза

P = 5 см × 4 = 20 см

Площадь геометрической фигуры

Площадь геометрической фигуры — это число, которое характеризует размер данной фигуры.

Следует уточнить, что речь в данном случае идёт о площади на плоскости. Плоскостью в геометрии называют любую плоскую поверхность, например: лист бумаги, земельный участок, поверхность стола.

Площадь измеряется в квадратных единицах. Под квадратными единицами подразумевают квадраты, стороны которых равны единице. Например, 1 квадратный сантиметр, 1 квадратный метр или 1 квадратный километр.

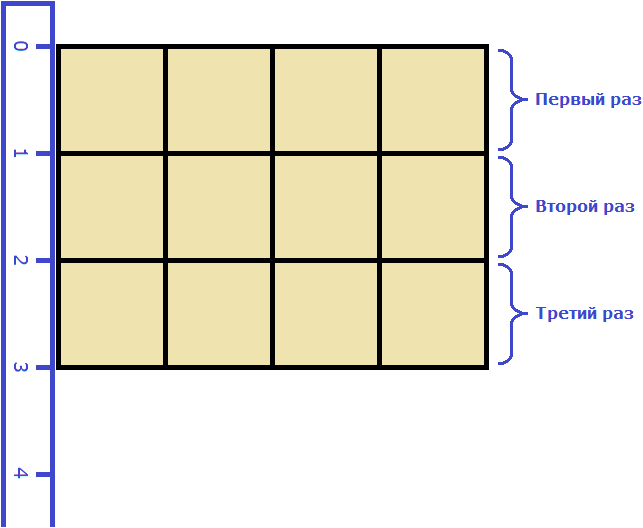
Измерить площадь какой-нибудь фигуры означает выяснить сколько квадратных единиц содержится в данной фигуре.

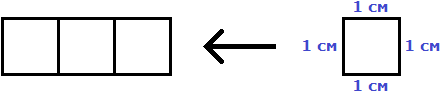
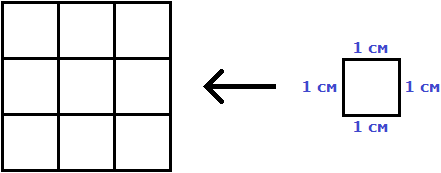
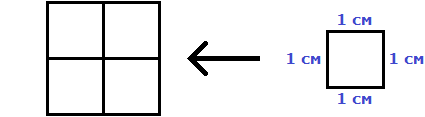
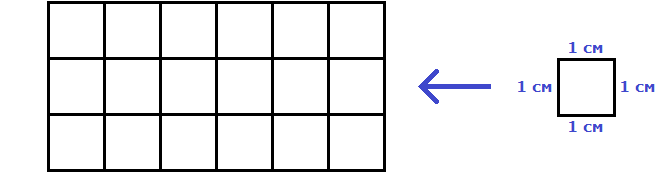
Например, площадь следующего прямоугольника равна трём квадратным сантиметрам:

Это потому что в данном прямоугольнике содержится три квадрата, каждый из которых имеет сторону, равную одному сантиметру:

Справа представлен квадрат со стороной 1 см (он в данном случае является квадратной единицей). Если посмотреть сколько раз этот квадрат входит в прямоугольник, представленный слева, то обнаружим, что он входит в него три раза.

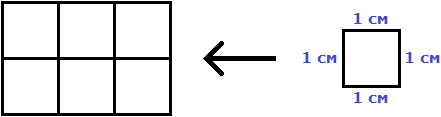
Следующий прямоугольник имеет площадь, равную шести квадратным сантиметрам:

Это потому что в данном прямоугольнике содержится шесть квадратов, каждый из которых имеет сторону, равную одному сантиметру:

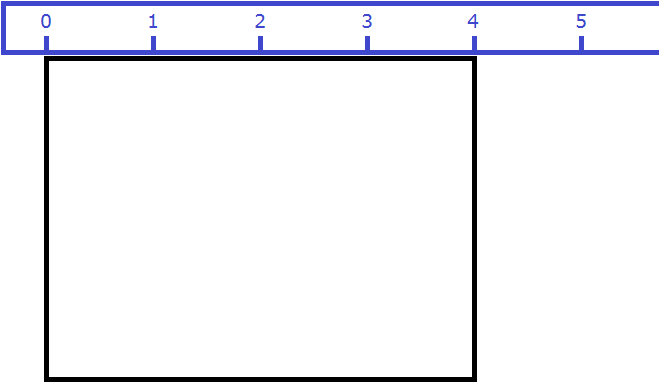
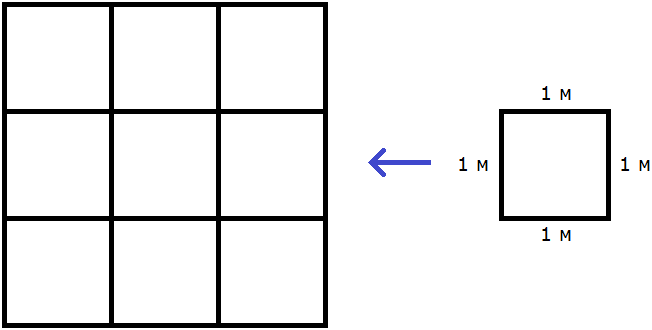
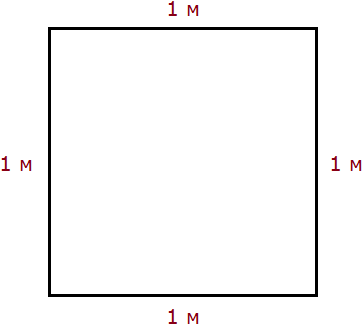
Допустим, потребовалось измерить площадь следующей комнаты:

Определимся в каких квадратах будем измерять площадь. В данном случае площадь удобно измерить в квадратных метрах:

Итак, наша задача состоит в том, чтобы определить сколько таких квадратов со стороной 1 м содержится в исходной комнате. Заполним этим квадратом всю комнату:

Видим, что квадратный метр содержится в комнате 12 раз. Значит, площадь комнаты составляет 12 квадратных метров.

Площадь прямоугольника

В предыдущем примере мы вычислили площадь комнаты, последовательно проверив сколько раз в ней содержится квадрат, сторона которого равна одному метру. Площадь составила 12 квадратных метров.

Комната представляла собой прямоугольник. Площадь прямоугольника можно вычислить перемножив его длину и ширину.

Чтобы вычислить площадь прямоугольника, нужно перемножить его длину и ширину.

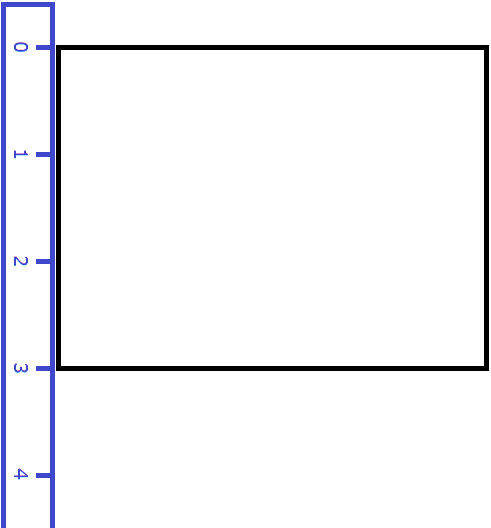
Вернёмся к предыдущему примеру. Допустим, мы измерили длину комнаты рулеткой и оказалось, что длина составила 4 метра:

Теперь измерим ширину. Пусть она составила 3 метра:

Умножим длину (4 м) на ширину (3 м).

4 × 3 = 12

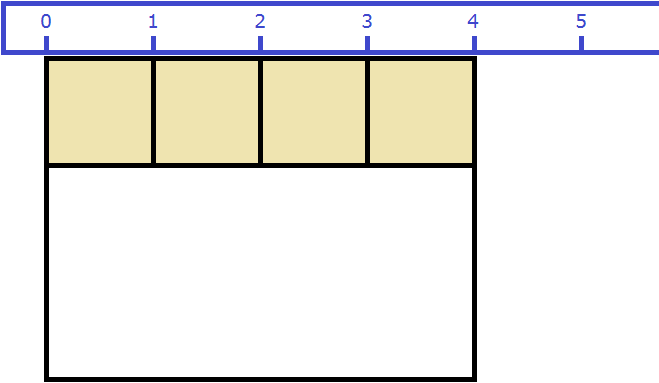
Как и в прошлый раз получаем двенадцать квадратных метров. Это объясняется тем, что измерив длину, мы тем самым узнаём сколько раз можно уложить в эту длину квадрат со стороной, равной одному метру. Уложим четыре квадрата в эту длину:

Затем мы определяем сколько раз можно повторить эту длину с уложенными квадратами. Это мы узнаём, измерив ширину прямоугольника:

Площадь квадрата

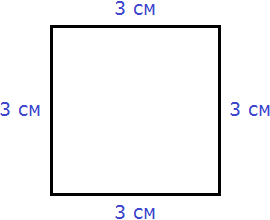
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, на следующем рисунке представлен квадрат со стороной 3 см. Фраза «квадрат со стороной 3 см» означает, что все стороны равны 3 см

Площадь квадрата вычисляется таким же образом, как и площадь прямоугольника — длину умножают на ширину.

Вычислим площадь квадрата со стороной 3 см. Умножим длину 3 см на ширину 3 см

3 × 3 = 9

В данном случае требовалось узнать сколько квадратов со стороной 1 см содержится в исходном квадрате. В исходном квадрате содержится девять квадратов со стороной 1 см. Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз:

Умножив длину на ширину, мы получили выражение 3 × 3, а это есть произведение двух одинаковых множителей, каждый из которых равен 3. Иными словами выражение 3 × 3 представляет собой вторую степень числа 3. А значит процесс вычисления площади квадрата можно записать в виде степени 3².

Поэтому вторую степень числа называют квадратом числа. При вычислении второй степени числа a, человек тем самым находит площадь квадрата со стороной a. Операцию возведения числа во вторую степень по другому называют возведением в квадрат.

Обозначения

Площадь обозначается заглавной латинской буквой S (англ. Square — квадрат). Тогда площадь квадрата со стороной a см будет вычисляться по следующему правилу

S = a²

где a — длина стороны квадрата. Вторая степень указывает на то, что происходит перемножение двух одинаковых сомножителей, а именно длины и ширины. Ранее было сказано, что у квадрата все стороны равны, а значит равны длина и ширина квадрата, выраженные через букву a.

Если задача состоит в том, чтобы определить сколько квадратов стороной 1 см содержится в исходном квадрате, то в качестве единиц измерения площади нужно указывать см². Это обозначение заменяет словосочетание «квадратный сантиметр».

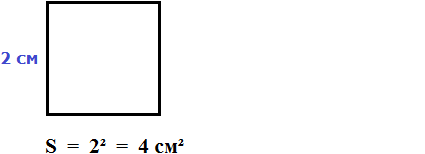
Например, вычислим площадь квадрат со стороной 2 см.

Значит, квадрат со стороной 2 см, имеет площадь, равную четырём квадратным сантиметрам:

Если задача состоит в том, чтобы определить сколько квадратов со стороной 1 м содержится в исходном квадрате, то в качестве единиц измерения нужно указывать м². Это обозначение заменяет словосочетание «квадратный метр».

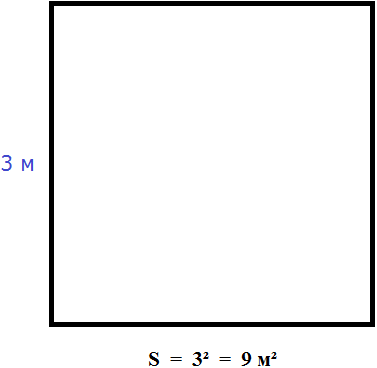
Вычислим площадь квадрата со стороной 3 метра

Значит, квадрат со стороной 3 м, имеет площадь равную девяти квадратным метрам:

Аналогичные обозначения используются при вычислении площади прямоугольника. Но длина и ширина прямоугольника могут быть разными, поэтому они обозначаются через разные буквы, например a и b. Тогда площадь прямоугольника, длиной a и шириной b вычисляется по следующему правилу:

S = a × b

Как и в случае с квадратом, единицами измерения площади прямоугольника могут быть см², м², км². Эти обозначения заменяют словосочетания «квадратный сантиметр», «квадратный метр», «квадратный километр» соответственно.

Например, вычислим площадь прямоугольника, длиной 6 см и шириной 3 см

Значит, прямоугольник длиной 6 см и шириной 3 см имеет площадь, равную восемнадцати квадратным сантиметрам:

В качестве единицы измерения допускается использовать словосочетание «квадратных единиц». Например, запись S = 3 кв.ед означает, что площадь квадрата или прямоугольника равна трём квадратам, каждый из которых имеет единичную сторону (1 см, 1 м или 1 км).

Перевод единиц измерения площади

Единицы измерения площади можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:

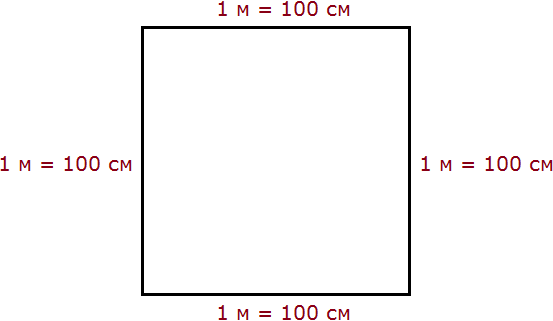
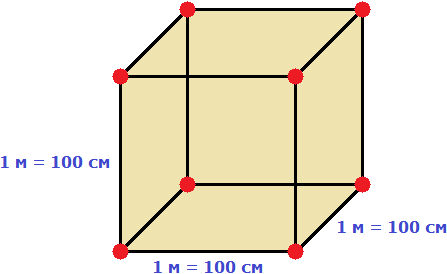
Пример 1. Выразить 1 квадратный метр в квадратных сантиметрах.

1 квадратный метр это квадрат со стороной 1 м. То есть все четыре стороны имеют длину, равную одному метру.

Но 1 м = 100 см. Тогда все четыре стороны тоже имеют длину, равную 100 см

Вычислим новую площадь этого квадрата. Умножим длину 100 см на ширину 100 см или возведём в квадрат число 100

S = 100² = 10 000 см²

Получается, что на один квадратный метр приходится десять тысяч квадратных сантиметров.

1 м² = 10 000 см²

Это позволяет в будущем умножить любое количество квадратных метров на 10 000 и получить площадь, выраженную в квадратных сантиметрах.

Чтобы перевести квадратные метры в квадратные сантиметры, нужно количество квадратных метров умножить на 10 000.

А чтобы перевести квадратные сантиметры в квадратные метры, нужно наоборот количество квадратных сантиметров разделить на 10 000.

Например, переведём 100 000 см² в квадратные метры. Рассуждать в этом случае можно так: «если 10 000 см² это один квадратный метр, то сколько раз 100 000 см² будут содержать по 10 000 см²»

100 000 см² : 10 000 см² = 10 м²

Другие единицы измерения можно переводить таким же образом. Например, переведём 2 км² в квадратные метры.

Один квадратный километр это квадрат со стороной 1 км. То есть все четыре стороны имеют длину, равную одному километру. Но 1 км = 1000 м. Значит, все четыре стороны квадрата также равны 1000 м. Найдём новую площадь квадрата, выраженную в квадратных метрах. Для этого умножим длину 1000 м на ширину 1000 м или возведём в квадрат число 1000

S = 1000² = 1 000 000 м²

Получается, что на один квадратный километр приходится один миллион квадратных метров:

1 км² = 1 000 000 м²

Это позволяет в будущем умножить любое количество квадратных километров на 1 000 000 и получить площадь, выраженную в квадратных метрах.

Чтобы перевести квадратные километры в квадратные метры, нужно количество квадратных километров умножить на 1 000 000.

Итак, вернёмся к нашей задаче. Требовалось перевести 2 км² в квадратные метры. Умножим 2 км² на 1 000 000

2 км² × 1 000 000 = 2 000 000 м²

А чтобы перевести квадратные метры в квадратные километры, нужно наоборот количество квадратных метров разделить на 1 000 000.

Например, переведём 3 500 000 м² в квадратные километры. Рассуждать в этом случае можно так: «если 1 000 000 м² это один квадратный километр, то сколько раз 3 500 000 м² будут содержать по 1 000 000 м²»

3 500 000 м² : 1 000 000 м² = 3,5 км²

Пример 2. Выразить 7 м² в квадратных сантиметрах.

Умножим 7 м² на 10 000

7 м² = 7 м² × 10 000 = 70 000 см²

Пример 3. Выразить 5 м² 13 см² в квадратных сантиметрах.

5 м² 13 см² = 5 м² × 10 000 + 13 см² = 50 013 см²

Пример 4. Выразить 550 000 см² в квадратных метрах.

Узнаем сколько раз 550 000 см² содержит по 10 000 см². Для этого разделим 550 000 см² на 10 000 см²

550 000 см² : 10 000 см² = 55 м²

Пример 5. Выразить 7 км² в квадратных метрах.

Умножим 7 км² на 1 000 000

7 км² × 1 000 000 = 7 000 000 м²

Пример 6. Выразить 8 500 000 м² в квадратных километрах.

Узнаем сколько раз 8 500 000 м² содержит по 1 000 000 м². Для этого разделим 8 500 000 м² на 1 000 000 м²

8 500 000 м² × 1 000 000 м² = 8,5 км²

Единицы измерения площади земельных участков

Площади небольших земельных участков удобно измерять в квадратных метрах.

Площади более крупных земельных участков измеряются в арах и гектарах.

Ар (сокращённо: a) — это площадь равная ста квадратным метрам (100 м²). В виду частого распространения такой площади (100 м²) она стала использоваться, как отдельная единица измерения.

Например, если сказано что площадь какого-нибудь поля составляет 3 а, то нужно понимать, что это три квадрата площадью 100 м² каждый, то есть:

3 а = 100 м² × 3 = 300 м²

В народе ар часто называют соткой, поскольку ар равен квадрату, площадью 100 м². Примеры:

1 сотка = 100 м²

2 сотки = 200 м²

10 соток = 1000 м²

Гектар (сокращенно: га) — это площадь, равная 10 000 м². Например, если сказано что площадь какого-нибудь леса составляет 20 гектаров, то нужно понимать, что это двадцать квадратов площадью 10 000 м² каждый, то есть:

20 га = 10 000 м² × 20 = 200 000 м²

Прямоугольный параллелепипед и куб

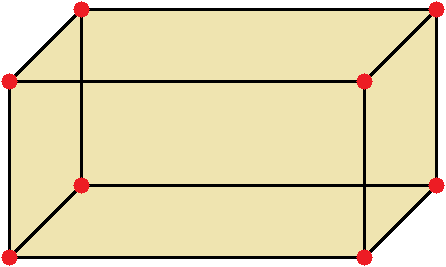
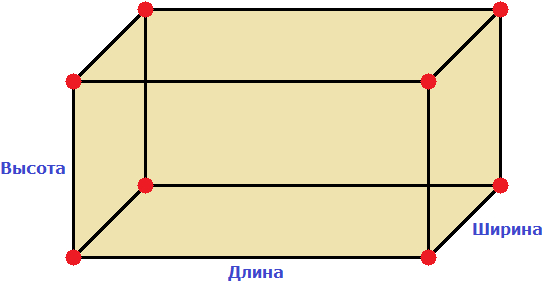
Прямоугольный параллелепипед — это геометрическая фигура, состоящая из грáней, рёбер и вершин. На рисунке показан прямоугольный параллелепипед:

Желтым цветом показаны грáни параллелепипеда, чёрным цветом — рёбра, красным — вершины.

Прямоугольный параллелепипед обладает длиной, шириной и высотой. На рисунке показано где длина, ширина и высота:

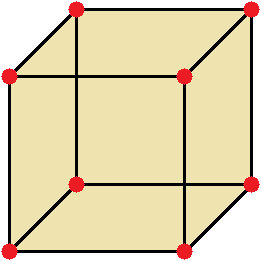
Параллелепипед, у которого длина, ширина и высота равны между собой, называется кубом. На рисунке показан куб:

куб

Объём геометрической фигуры

Объём геометрической фигуры — это число, которое характеризует вместимость данной фигуры.

Объём измеряется в кубических единицах. Под кубическими единицами подразумевают кубы длиной 1, шириной 1 и высотой 1. Например, 1 кубический сантиметр или 1 кубический метр.

Измерить объём какой-нибудь фигуры означает выяснить сколько кубических единиц вмещается в данную фигуру.

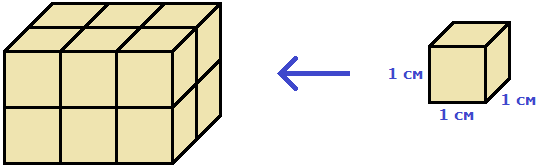
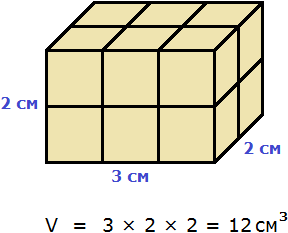
Например, объём следующего прямоугольного параллелепипеда равен двенадцати кубическим сантиметрам:

Это потому что в данный параллелепипед вмещается двенадцать кубов длиной 1 см, шириной 1 см и высотой 1 см:

Объём обозначается заглавной латинской буквой V. Одна из единиц измерения объема это кубический сантиметр (см³). Тогда объём V рассмотренного нами параллелепипеда равен 12 см³

V = 12 см³

Объём любого параллелепипеда вычисляют следующим образом: перемножают его длину, ширину и высоту .

Объём прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.

V = abc

где, a — длина, b — ширина, c — высота

Так, в предыдущем примере мы визуально определили, что объём параллелепипеда равен 12 см³. Но можно измерить длину, ширину и высоту данного параллелепипеда и перемножить результаты измерений. Мы получим тот же результат

Объём куба вычисляется таким же образом, как и объём прямоугольного параллелепипеда — перемножают длину, ширину и высоту.

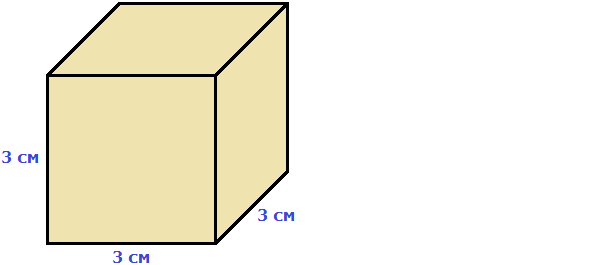
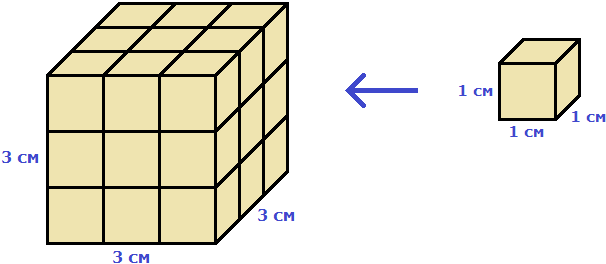
Например, вычислим объём куба, длина которого 3 см. У куба длина, ширина и высота равны между собой. Если длина равна 3 см, то равны этим же трём сантиметрам ширина и высота куба:

Перемножаем длину, ширину, высоту и получаем объём, равный двадцати семи кубическим сантиметрам:

V = 3 × 3 × 3 = 27 см³

Действительно, в исходный куб вмещается 27 кубиков длиной 1 см

При вычислении объёма данного куба мы перемножили длину, ширину и высоту. Получилось произведение 3 × 3 × 3. Это есть произведение трёх сомножителей, каждый из которых равен 3. Иными словами, произведение 3 × 3 × 3 является третьей степенью числа 3 и может быть записано в виде 3³.

V = 3³ = 27 см³

Поэтому третью степень числа называют кубом числа. При вычислении третьей степени числа a, человек тем самым находит объём куба, длиной a. Операцию возведения числа в третью степень по другому называют возведением в куб.

Таким образом, объём куба вычисляется по следующему правилу:

V = a³

Где a — длина куба.

Кубический дециметр. Кубический метр

Не все объекты нашего мира удобно измерять в кубических сантиметрах. Например, объём комнаты или дома удобнее измерять в кубических метрах (м³). А объём бака, аквариума или холодильника удобнее измерять в кубических дециметрах (дм³).

Другое название одного кубического дециметра – один литр.

1 дм³ = 1 литр

Перевод единиц измерения объёма

Единицы измерения объёма можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:

Пример 1. Выразить 1 кубический метр в кубических сантиметрах.

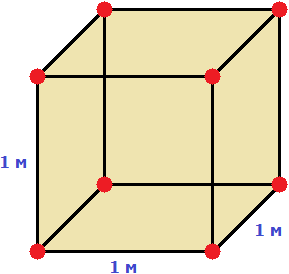
Один кубический метр это куб со стороной 1 м. Длина, ширина и высота этого куба равны одному метру.

Но 1 м = 100 см. Значит, длина, ширина и высота тоже равны 100 см

Вычислим новый объём куба, выраженный в кубических сантиметрах. Для этого перемножим его длину, ширину и высоту. Либо возведём число 100 в куб:

V = 100³ = 1 000 000 см³

Получается, что на один кубический метр приходится один миллион кубических сантиметров:

1 м³ = 1 000 000 см³

Это позволяет в будущем умножить любое количество кубических метров на 1 000 000 и получить объём, выраженный в кубических сантиметрах.

Чтобы перевести кубические метры в кубические сантиметры, нужно количество кубических метров умножить на 1 000 000.

А чтобы перевести кубические сантиметры в кубические метры, нужно наоборот количество кубических сантиметров разделить на 1 000 000.

Например, переведём 300 000 000 см³ в кубические метры. Рассуждать в этом случае можно так: «если 1 000 000 см³ это один кубический метр, то сколько раз 300 000 000 см³ будут содержать по 1 000 000 см³»

300 000 000 см³ : 1 000 000 см³ = 300 м³

Пример 2. Выразить 3 м³ в кубических сантиметрах.

Умножим 3 м³ на 1 000 000

3 м³ × 1 000 000 = 3 000 000 см³

Пример 3. Выразить 60 000 000 см³ в кубических метрах.

Узнаем сколько раз 60 000 000 см³ содержит по 1 000 000 см³. Для этого разделим 60 000 000 см³ на 1 000 000 см³

60 000 000 см³ : 1 000 000 см³ = 60 м³

Вместимость бака, банки или канистры измеряют в литрах. Литр это тоже единица измерения объема. Один литр равен одному кубическому дециметру.

1 литр = 1 дм³

Например, если вместимость банки составляет 1 литр, это значит что объём этой банки составляет 1 дм³. При решении некоторых задач может быть полезным умение переводить литры в кубические дециметры и наоборот. Рассмотрим несколько примеров.

Пример 1. Перевести 5 литров в кубические дециметры.

Чтобы перевести 5 литров в кубические дециметры, достаточно умножить 5 на 1

5 л × 1 = 5 дм³

Пример 2. Перевести 6000 литров в кубические метры.

Шесть тысяч литров это шесть тысяч кубических дециметров:

6000 л × 1 = 6000 дм³

Теперь переведём эти 6000 дм³ в кубические метры.

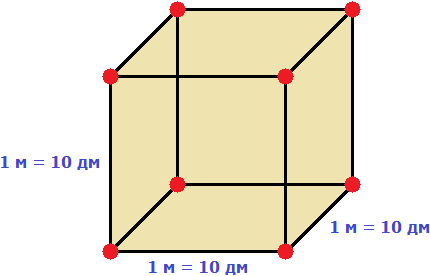
Длина, ширина и высота одного кубического метра равны 10 дм

Если вычислить объём этого куба в дециметрах, то получим 1000 дм³

V = 10³= 1000 дм³

Получается, что одна тысяча кубических дециметров соответствует одному кубическому метру. А чтобы определить сколько кубических метров соответствуют шести тысячамл кубических дециметров, нужно узнать сколько раз 6 000 дм³ содержит по 1 000 дм³

6 000 дм³ : 1 000 дм³ = 6 м³

Значит, 6000 л = 6 м³.

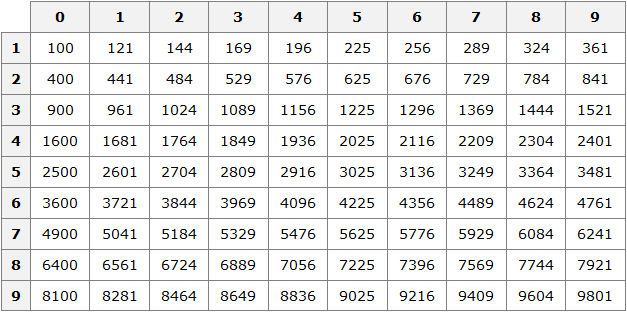
Таблица квадратов

В жизни часто приходиться находить площади различных квадратов. Для этого каждый раз требуется возводить исходное число во вторую степень.

Квадраты первых 99 натуральных чисел уже вычислены и занесены в специальную таблицу, называемую таблицей квадратов.

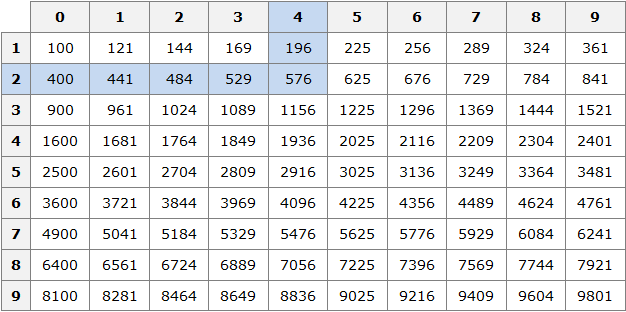
Первая строка данной таблицы (цифры от 0 до 9) это единицы исходного числа, а первый столбец (цифры от 1 до 9) это десятки исходного числа.

Например, найдём квадрат числа 24 по данной таблице. Число 24 состоит из цифр 2 и 4. Точнее, число 24 состоит из двух десятков и четырёх единиц.

Итак, выбираем цифру 2 в первом столбце таблицы (столбце десятков), а цифру 4 выбираем в первой строке (строке единиц). Затем, двигаясь вправо от цифры 2 и вниз от цифры 4, найдём точку пересечения. В результате окажемся на позиции, где располагается число 576. Значит, квадрат числа 24 есть число 576

24² = 576

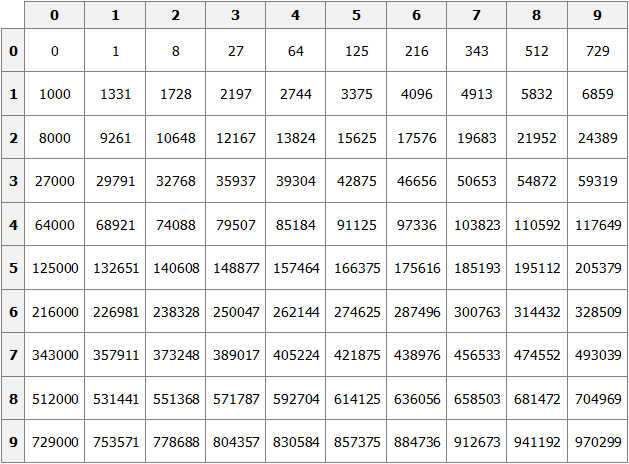
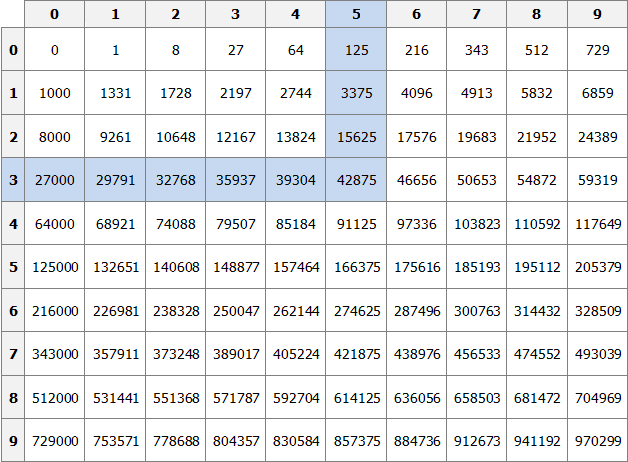
Таблица кубов

Как и в ситуации с квадратами, кубы первых 99 натуральных чисел уже вычислены и занесены в таблицу, называемую таблицей кубов.

Куб числа по таблице определяется таким же образом, как и квадрат числа. Например, найдём куб числа 35. Это число состоит из цифр 3 и 5. Выбираем цифру 3 в первом столбце таблицы (столбце десятков), а цифру 5 выбираем в первой строке (строке единиц). Двигаясь вправо от цифры 3 и вниз от цифры 5, найдём точку пересечения. В результате окажемся на позиции, где располагается число 42875. Значит, куб числа 35 есть число 42875.

35³ = 42875

Задания для самостоятельного решения

Задача 1. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите периметр.

Решение

P = 2(a + b)

a = 6, b = 2
P = 2(6 + 2) = 12 + 4 = 16 см

Ответ: периметр прямоугольника равен 16 см.

Задача 2. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите площадь.

Решение

S = ab
a = 6, b = 2
S = 6 × 2 = 12 см²

Ответ: площадь равна 12 см².

Задача 3. Площадь прямоугольника составляет 12 см². Длина составляет 6 см. Найдите ширину прямоугольника.

Решение

S = ab
S = 12, a = 6, b = x
12 = 6 × x
x = 2

Ответ: ширина прямоугольника составляет 2 см.

Задача 4. Вычислите площадь квадрата со стороной 8 см

Решение

S = a²
a = 8
S = 8²= 64 см²
Ответ: площадь квадрата со стороной 8 см равна 64 см²

Задача 5. Вычислите объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см.

Решение

V = abc
a = 6, b = 4, c = 3
V = 6 × 4 × 3 = 72 см³.

Ответ: объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см равен 72 см³

Задача 6. Объем прямоугольного параллелепипеда составляет 200 см³. Найдите высоту параллелепипеда, если его длина равна 10 см, а ширина 5 см

Решение

V = abc
V = 200, a = 10, b = 5, c = x
200 = 10 × 5 × x
200 = 50x
x = 4

Ответ: высота прямоугольного параллелепипеда равна 4 см.

Задача 7. Площади земельного участка, засеянные пшеницей и льном, пропорциональны числам 4 и 5. На какой площади засеяна пшеница, если под льном засеяно 15 га

Решение

Число 4 отражает площадь, засеянную пшеницей. А число 5 отражает площадь, засеянную льном.
Сказано что площади, засеянные пшеницей и льном пропорциональны этим числам.

Проще говоря, во сколько раз изменяются числа 4 или 5, во сколько же раз изменится и площадь, которая засеяна пшеницей или льном. Льном засеяно 15 га. То есть число 5, которое отражает площадь, засеянную льном, изменилось в 3 раза.

Тогда число 4, которое отражает площадь засеянную пшеницей, нужно увеличить в три раза

4 × 3 = 12 га

Ответ: пшеницей засеяно 12 га.

Задача 8. Длина зернохранилища 42 м, ширина составляет длины, а высота – 0,1 длины. Определите сколько тонн зерна вмещает зернохранилище, если 1 м³ его весит 740 кг.

Решение

a — длина
b — ширина
c — высота

a = 42 м
b = 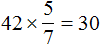м
c = 42 × 0,1 = 4,2 м

Определим объем зернохранилища:

V = abc = 42 × 30 × 4,2 = 5292 м³

Определите сколько тонн зерна вмещает зернохранилище:

5292 × 740 = 3916080 кг

Переведём килограммы в тонны:

Ответ: зернохранилище вмещает 3916,08 тонн зерна.

Задача 9. 12. Бассейн имеет форму прямоугольного параллелепипеда, длина которого равна 5,8 м, а ширина – 3,5 м. Две трубы наполняют его водой в течение 13 ч 32 мин., причём через одну из них вливается 25 л/мин, а через вторую – 0,75 этого количества. Определите высоту (глубину) бассейна.

Решение

Определим сколько литров в минуту вливается через вторую трубу:

25 л/мин × 0,75 = 18,75 л/мин

Определим сколько литров в минуту вливается в бассейн через обе трубы:

25 л/мин + 18,75 л/мин = 43,75 л/мин

Определим сколько литров воды будет залито в бассейн за 13 ч 32 мин

43,75 × 13 ч 32 мин = 43,75 × 812 мин = 35 525 л

1 л = 1 дм³

35 525 л = 35 525 дм³

Переведём кубические дециметры в кубические метры. Это позволит вычислит объем бассейна:

35 525 дм³ : 1000 дм³ = 35,525 м³

Зная объём бассейна можно вычислить высоту бассейна. Подставим в буквенное уравнение V=abc имеющиеся у нас значения. Тогда получим:

V = 35,525
a = 5.8
b = 3.5
c = x

35,525 = 5,8 × 3,5 × x
35,525 = 20,3 × x
x = 1,75 м

с = 1,75

Ответ: высота (глубина) бассейна составляет 1,75 м.

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Источник

Загрузить PDF

Нахождение периметра фигуры – порой непростая задача. Эта статья научит вас находить периметры следующих основных фигур: прямоугольника, квадрата, круга, прямоугольного треугольника, треугольника и правильного многоугольника.

1
Найдите длины двух смежных сторон: ширины и высоты. Прямоугольник – фигура с четырьмя сторонами, которые пересекаются под прямым углом, а две противоположные стороны параллельны и равны. Таким образом, две смежные стороны имеют разную длину (ширина и высота; если ширина равна высоте, то такая фигура – квадрат).
- Если даны только одна сторона и площадь прямоугольника, вы можете найти другую сторону по формуле: A=wh, то есть h=A/w или w=A/h. Поэтому, если даны высота и площадь, просто разделите площадь на высоту, чтобы найти ширину. Вы также можете разделить площадь на ширину, чтобы найти высоту.
2

Сложите длины двух смежных сторон и умножьте полученное значение на 2. Если w – ширина и h – высота, периметр прямоугольника: P=2(w+h)

Реклама

1

Найдите длину стороны квадрата (назовем ее х). Квадрат – фигура, у которой все стороны равны и пресекаются под прямым углом.
2
Если дана площадь (A) квадрата, вы можете найти длину стороны, взяв квадратный корень из площади: х = √ (A).
- Если дана диагональ (d) квадрата, Вы можете найти длину стороны, разделив диагональ на квадратный корень из 2: х = d/√2
3

Умножьте длину стороны на четыре. Поскольку все четыре стороны имеют одинаковую длину, периметр квадрата равен учетверенной длине одной стороны: Р = 4x.

Реклама

1
Найдите длину радиуса (r). Радиус является расстоянием от центра круга до любой точки на окружности.
- Если дан диаметр (d) круга, вы можете найти радиус, разделив диаметр на два: г = d/2
- Если дана площадь (A) круга, вы можете найти радиус, разделив площадь на π, а затем взяв квадратный корень из полученного значения: г = √(A/π)
2
Найдите периметр, умножив радиус на 2π: Р = 2πr.
- Так как диаметр – это удвоенный радиус, периметр может быть найден по формуле: P = πd.
Реклама

1

Найдите длины двух сторон треугольника (а и b), пересекающихся под прямым углом.
2

Найдите сумму квадратов а и b, а затем извлеките квадратный корень из полученной суммы: √(а^2 + b^2). По теореме Пифагора, а^2 + b^2 = с^2, где с – длина гипотенузы, то есть стороны, лежащей напротив прямого угла.
3

Теперь, когда у вас есть а, b и с (все три стороны треугольника), просто сложите их для нахождения периметра: P = а+b+с.

Реклама

1

Найдите высоту треугольника (у) и его основание (х) (сторона, к которой проведен перпендикуляр – высота).
2

Найдите длины отрезков х1 и х2, на которые высота делит основание (то есть х = х1 + х2). Высота делит треугольник на два прямоугольных треугольника (один с катетами х1 и у, другой с катетами х2 и у), и необходимо найти длины гипотенуз этих треугольников с1 и с2.
3

Найдите с1 и с2. Для этого используйте теорему Пифагора: а^2 + b^2 = с^2, и подставьте x1 вместо a, y вместо b, c1 вместо c. Повторите для х2, у, и с2.
4

Сложите х, с1 и с2, которые являются тремя сторонами исходного треугольника.

Реклама

1
Найдите длину одной стороны правильного многоугольника. По определению, правильный многоугольник – это фигура с равными сторонами и углами.
- Если дана апофема (перпендикуляр, опущенный из центра многоугольника к одной из его сторон), Вы можете найти длину стороны. Если n – число сторон многоугольника, А – длина апофемы, длина стороны: x=2Atan(180/n).
- Если дан радиус (расстояние между центром и любой вершиной), вы можете найти длину стороны: x=2rsin(180/n), где r – радиус, n – число сторон многоугольника.
2

Умножьте длину одной стороны многоугольника на число его сторон. Таким образом, P=nx, где n – число сторон многоугольника, х – длина одной стороны многоугольника.

Реклама

Об этой статье

Эту страницу просматривали 16 024 раза.

Была ли эта статья полезной?

Источник

Как найти периметр многоугольника

Ваши комментарии

Video

References

About This Article

Did this article help you?

Периметр геометрической фигуры

Площадь геометрической фигуры

Площадь прямоугольника

Площадь квадрата

Обозначения

Перевод единиц измерения площади

Единицы измерения площади земельных участков

Прямоугольный параллелепипед и куб

Объём геометрической фигуры

Кубический дециметр. Кубический метр

Перевод единиц измерения объёма

Таблица квадратов

Таблица кубов

Задания для самостоятельного решения

Об этой статье

Была ли эта статья полезной?

Вам также может понравиться

Как найти цвет кузова на машине

Как найти стоимость со скидкой в excel

Как найти высоту параллельного параллелепипеда

Добавить комментарий Отменить ответ