Среди геометрических фигур очень большую часть составляют многоугольники. Это квадрат, прямоугольник, параллелограмм, ромб, треугольник, трапеция и другие n-угольники (n — количество сторон многоугольника).
Периметр любого многоугольника – это сумма длин всех его сторон.
Онлайн-калькулятор периметра многоугольника
Формула периметра многоугольника
P=a+b+c+d+e+…P=a+b+c+d+e+…,
где a,b,c,d,e,…a, b, c, d, e,… — длины сторон многоугольника.
Частным случаем многоугольника является так называемый правильный многоугольник.
Правильный многоугольник – это такой многоугольник, у которого все стороны равной длины.
Если говорить о периметре правильного многоугольника, то его можно найти, умножив длину стороны фигуры на количество сторон.
P=n⋅aP=ncdot a
aa — длина стороны многоугольника;
nn — количество сторон многоугольника.
Разберем задачи на нахождение периметра правильного и неправильного многоугольников.
Найти периметр правильного шестиугольника со стороной 10 см.
Решение
a=10a=10
n=6n=6
Воспользуемся формулой для нахождения периметра правильного шестиугольника и подставим вместо aa численное значение:
P=n⋅a=6⋅10=60P=ncdot a=6cdot 10=60 см.
Ответ: P=60P=60 см.
Стороны многоугольника равны 6 см, 5 см, 2 см, 3 см и 1 см. Найти периметр данной фигуры.
Решение
a=6a=6
b=5b=5
c=2c=2
d=3d=3
e=1e=1
В данной задаче нам дан неправильный многоугольник, так как его стороны разной длины. В этом случае нам подходит первая стандартная формула нахождения периметра. Сложим длины всех сторон многоугольника и найдем его периметр:
P=a+b+c+d+e=6+5+2+3+1=17P=a+b+c+d+e=6+5+2+3+1=17 см.
Ответ: P=17P=17 см.
Ищете, где где можно заказать контрольную работу недорого? Обратитесь к нашим экспертам!
Тест по теме “Периметр многоугольника”
Download Article
Download Article
A polygon is any two-dimensional shape that has straight lines. There are both regular polygons, which are shapes with equal sides, and irregular polygons, which are shapes with different side lengths. The methods for finding the perimeter of regular and irregular polygons are a little different, but both are simple once you know what to do. You can also find the perimeter of them on a coordinate grid. If you’re trying to find the perimeter of a regular polygon, just use the formula: perimeter = number of sides x the length of any side.
-
1
Check that the sides of the polygon are all the same length. Regular polygons are polygons that have equal sides. If the sides of the polygon you’re looking at aren’t all the same length, you’ll need to find the perimeter using the method for irregular polygons instead. If the side lengths are equal, you’re working with a regular polygon.[1]
Tip: If some of the sides aren’t labeled, try looking at the rest of the polygon to determine what the lengths are. For example, if you have a square with only 1 labeled side, you know the other sides are the same length since squares have equal sides.
-
2
Write down the length of 1 side of the polygon. It doesn’t matter which side you choose since all of the side lengths are equal. Just make sure you’re only writing down the length of 1 side.[2]
- For example, if you’re working with a square that has a side length of 6, you would write down “6.”
Advertisement
-
3
Write down the total number of sides that the polygon has. Don’t worry about the side lengths at this point. Just count how many sides the polygon has and write it down.[3]
- For a square, you’d write down “4” since a square has 4 sides.
-
4
Multiply the side length by the number of sides to get the perimeter. The formula for finding the perimeter of a regular polygon is just the number of sides x the length of any side. Once you’ve multiplied those 2 numbers together, you’ve found the perimeter of the polygon![4]
- In the square example, you know that the square has a side length of 6 and a total of 4 sides. Therefore, you’d just multiply 6 by 4 to get 24, which would be the perimeter of the square.
- Or, say you were working with a triangle that has a side length of 3. Since a triangle has 3 sides, you would multiply 3 (the number of sides) by 3 (the side length) to get 9. Therefore, the perimeter of the triangle would be 9.
Advertisement
-
1
Look at the length of the polygon’s sides to determine if it’s irregular. An irregular polygon is a polygon that doesn’t have equal sides. If the sides of the polygon are all the same length, that means the polygon is regular, not irregular.[5]
Did you know? You can use the same method for finding the perimeter of an irregular polygon to find the perimeter of a regular polygon, but not the other way around.
-
2
Write down the length of each side of the polygon. Since not all sides of an irregular polygon are equal, you’ll need to write out each individual side length. Even if some of the sides are equal, you should still write each length out individually.[6]
- For example, if you’re working with a rectangle that has 2 sides that are 4 units long and 2 sides that are 3 units long, you would write “4, 4, 3, 3.”
- If you’re working with an irregular polygon that has 1 side that’s 2 units, 1 side that’s 3 units, and 1 side that’s 4 units, you would write “2, 3, 4.”
-
3
Add up all of the lengths to find the perimeter. To find the perimeter of an irregular polygon, all you need to do is find the total of all of its side lengths. Simply add up each side length that you wrote down to find the perimeter of the polygon![7]
- For example, if the side lengths for the polygon were 4, 4, 3, and 3, they would add up to 14. Therefore, 14 would be the perimeter of the polygon.
Advertisement
-
1
Draw a coordinate grid with an x- and y-axis. A coordinate grid is a graph with an x- and y-axis that you can plot coordinates on. To draw a coordinate grid, get a piece of graph paper or draw your own grid lines on a blank piece of paper using a ruler. Then, draw a horizontal line through the middle for the x-axis and a vertical line down the center for the y-axis. Finally, number the points on each axis, starting with “0” where the x- and y-axis intersect.[8]
- When you number your grid, the numbers above and to the right of the 0 will be positive, while the numbers below and to the left of the 0 will be negative.
-
2
Plot the given coordinates on the graph. You should have been given coordinates for each vertex, or angular point, of the polygon you’re trying to find the perimeter of. Each coordinate should look something like “(1,2).” Use the numbers you marked on the coordinate grid to plot each of the coordinates. When you’re finished, connect the points with straight lines to see the shape of the polygon you’re working with.[9]
Tip: When plotting coordinates, remember that the first number represents the x-axis and the second number represents the y-axis. For example, if you were plotting (2,4), you would count 2 over on the x-axis and 4 up on the y-axis and then mark where those 2 points meet on the grid.
-
3
Find vertical and horizontal side lengths by counting the units. You’ll need to know the length of each side of the polygon to determine its perimeter. For vertical or horizontal sides, simply count how many units there are between the points on each end. Then, write down the number next to that side so you can refer to it later.[10]
- For example, if you’re trying to find the length of a horizontal side, start at one end and count the number of boxes between that point and the other end. If you counted 6, that would mean the length of that side is 6 units.
-
4
Use the distance formula to find the length of diagonal sides. Unfortunately, you can’t count the units on a grid to find the length of diagonal sides like you can with vertical or horizontal sides. Instead, you’ll need to use the distance formula, which is
. Just plug in the values of the x and y coordinates for the 2 points at the ends of the side you’re trying to find the distance of and solve to find the length.[11]
- For example, if you’re trying to find the distance (length) between 2 points with the coordinates (4,7) and (1,3), you would plug those coordinates into the formula and get
- Then, you would simplify the equation to get
.
- Finally, you would solve
and get 5. Therefore, the length of the side would be 5.
- For example, if you’re trying to find the distance (length) between 2 points with the coordinates (4,7) and (1,3), you would plug those coordinates into the formula and get
-
5
Add the length of each side together to find the polygon’s perimeter. The perimeter of a polygon is equal to the sum of all of its side lengths. Once you’ve determined all of these lengths using the coordinates you were given, all you need to do is add them together and then you’re done!
- For example, if you plotted the coordinates of a triangle and found that the side lengths are 3, 2, and 5, you would add these numbers together to get 10. Therefore, the perimeter of the triangle is 10.
Advertisement
Add New Question
-
Question
What should I do when I don’t feel motivated to do homework?
Jake Adams is an academic tutor and the owner of Simplifi EDU, a Santa Monica, California based online tutoring business offering learning resources and online tutors for academic subjects K-College, SAT & ACT prep, and college admissions applications. With over 14 years of professional tutoring experience, Jake is dedicated to providing his clients the very best online tutoring experience and access to a network of excellent undergraduate and graduate-level tutors from top colleges all over the nation. Jake holds a BS in International Business and Marketing from Pepperdine University.
Academic Tutor
Expert Answer
Support wikiHow by
unlocking this expert answer.First, create a plan for doing the homework and build in breaks or rewards. For example, get one task done and then set a reward for yourself to take a 15-minute break to call a friend or to go outside for a walk.
-
Question
If I get stressed while studying, how can I stay positive so I can do better on exams?
Jake Adams is an academic tutor and the owner of Simplifi EDU, a Santa Monica, California based online tutoring business offering learning resources and online tutors for academic subjects K-College, SAT & ACT prep, and college admissions applications. With over 14 years of professional tutoring experience, Jake is dedicated to providing his clients the very best online tutoring experience and access to a network of excellent undergraduate and graduate-level tutors from top colleges all over the nation. Jake holds a BS in International Business and Marketing from Pepperdine University.
Academic Tutor
Expert Answer
Support wikiHow by
unlocking this expert answer.Build a positive reinforcement loop for yourself by having a plan. For example, take the test day and then work backwards from that and decide what things you need to get done during the time you have. Then work towards those things. It’s putting one foot in front of the other. It’s also being realistic. If you realize the plan is not possible, but you’ll still get through about 80% of it, you’re still going to probably do okay in the class. You’ve done the best that you can. It takes this weight off of your shoulders of having to be perfect. Instead, it’s I have to do the best that I can in any given circumstance and that’s all I can do.
-
Question
How do you find the perimeter and area of a polygon?
This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.
wikiHow Staff Editor
Staff Answer
Support wikiHow by
unlocking this staff-researched answer.To find the perimeter, add up the lengths of all the sides of the polygon. Finding the area can be a little more complicated, since it depends on what kind of shape you’re dealing with. To calculate the area of a regular polygon, multiply ½ x p (the perimeter) x a (the apothem, or the distance from the center of the polygon to the midpoint of any side). If the polygon is irregular, you’ll need to divide it up into regular shapes (e.g., a rectangle and a triangle), find the area of each part, and add them together.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
References
About This Article
Article SummaryX
To find the perimeter of a regular polygon, which is a polygon with equal sides, start by writing down the length of 1 side and the total number of sides. Then, multiply those 2 numbers together to find the perimeter. If you’re trying to find the perimeter of an irregular polygon, which is a polygon with different side lengths, start by writing down the length of each side. Then, simply add up all of the lengths to find the perimeter. To learn how to find the perimeter of a polygon using coordinates, scroll down!
Did this summary help you?
Thanks to all authors for creating a page that has been read 155,167 times.
Did this article help you?
Загрузить PDF
Загрузить PDF
Многоугольник — это двумерная фигура, которая ограничена замкнутой ломаной линией (без самопересечений). Существуют правильные многоугольники, все стороны которых равны, и неправильные многоугольники, длины сторон которых различны. Процессы вычисления периметров правильного и неправильного многоугольников немного различаются, но они просты, если знать, что делать. Также периметры правильных и неправильных многоугольников можно найти, если фигуры построить на плоскости координат. Периметр правильного многоугольника можно вычислить по формуле: периметр = количество сторон x длина любой стороны.
-
1
Убедитесь, что стороны многоугольника равны. Правильный многоугольник — это многоугольник с равными сторонами. Если стороны многоугольника не равны, воспользуйтесь методом вычисления периметра неправильного многоугольника.[1]
Если длины всех сторон не даны, обратите внимание на форму многоугольника, чтобы попытаться определить их. Например, если дан квадрат с одной известной стороной, остальные стороны будут той же длины, потому что стороны квадрата равны.
-
2
Запишите значение одной стороны многоугольника. Выберите любую сторону, так как в правильном многоугольнике все стороны равны. Просто убедитесь, что записываете значение только одной стороны.[2]
- Например, если дан квадрат со стороной 6 см, запишите «6 см».
-
3
Запишите количество сторон многоугольника. Не думайте о длинах других сторон — просто подсчитайте, сколько сторон у многоугольника, и запишите это число.[3]
- В случае квадрата запишите «4», так как у квадрата 4 стороны.
-
4
Перемножьте значение стороны на количество сторон, чтобы вычислить периметр. Формула для нахождения периметра правильного многоугольника: периметр = количество сторон x длину любой стороны.[4]
- В нашем примере значение стороны квадрата 6 см и у квадрата 4 стороны. Поэтому 6 х 4 = 24 см — это периметр квадрата.
- Другой пример: дан треугольник с боковой длиной 3 см. У треугольника 3 стороны, поэтому 3 х 3 = 9 см — это периметр треугольника.
Реклама
-
1
Посмотрите на длины сторон многоугольника, чтобы определить, является ли он неправильным. У неправильного многоугольника стороны не равны (многоугольник с равными сторонами называется правильным).[5]
Запомните: метод для вычисления периметра неправильного многоугольника можно применять к правильным многоугольникам, но не наоборот.
-
2
Запишите значение каждой стороны многоугольника. Сделайте это, так как у неправильного многоугольника стороны разные. Даже если некоторые из сторон равны, все равно запишите длину каждой стороны.[6]
- Например, если дан прямоугольник, две стороны которого равны 4 см, а другие две 3 см, запишите «4 см, 4 см, 3 см, 3 см».
- Если дан неправильный многоугольник, одна сторона которого равна 2 см, вторая равна 3 см, третья равна 4 см, запишите «2 см, 3 см, 4 см».
-
3
Сложите значения всех сторон, чтобы найти периметр неправильного многоугольника. Просто сложите все значения, которые вы записали, и получите периметр многоугольника.[7]
- В нашем примере с прямоугольником: 4 + 4 + 3 + 3 = 14 см — это периметр многоугольника.
Реклама
-
1
Нарисуйте плоскость координат с осями X и Y. На плоскость координат нужно нанести точки с заданными координатами. Чтобы нарисовать плоскость координат, возьмите бумагу в клетку или с помощью линейки нарисуйте сетку на чистом листе бумаги. Теперь нарисуйте горизонтальную прямую (ось Х) и перпендикулярно ей посередине проведите вертикальную прямую (ось Y). Точку пересечения двух прямых пометьте как «0».[8]
- Когда будете наносить координатные метки, цифры над и справа «0» будут положительными, а цифры под и слева «0» будут отрицательными.
-
2
Нанесите точки с заданными координатами на координатную плоскость. В задаче будут даны координаты всех вершин многоугольника, периметр которого нужно найти. Каждая пара координат записывается так: (1,2). Используйте координатные метки, чтобы нанести точки на плоскость координат. Когда вы нанесете все точки, соедините их прямыми линиями, чтобы построить многоугольник.[9]
Запомните: первое число в паре координат (координата «х») откладывается по оси Х, а второе число (координата «y») — по оси Y. Например, чтобы нанести точку с координатами (2,4), отсчитайте 2 метки по оси Х и 4 метки по оси Y, а затем отметьте точку пересечения.
-
3
Найдите значения вертикальных и горизонтальных сторон. Необходимо знать длину каждой стороны многоугольника, чтобы определить ее периметр. В случае вертикальной или горизонтальной стороны просто посчитайте число координатных меток между точками стороны. Затем запишите число возле этой стороны.[10]
- Например, чтобы найти длину горизонтальной стороны, начните с одного ее конца и посчитайте число координатных меток до другого конца стороны. Если вы насчитали 6 меток, длина этой стороны составляет 6 единиц.
-
4
-
5
Сложите длины всех сторон многоугольника, чтобы найти его периметр. Периметр многоугольника равен сумме всех его сторон. Когда вы вычислите значения каждой стороны многоугольника по данным координатам точек его вершин, просто сложите эти значения.
- Например, если на координатной плоскости вы построили треугольник и вычислили, что его стороны равны 3, 2 и 5, сложите эти числа, чтобы получить 10. Таким образом, периметр треугольника равен 10 единиц.
Реклама
Об этой статье
Эту страницу просматривали 187 606 раз.
Была ли эта статья полезной?
Формула расчета периметра многоугольника
Содержание:
-
Что такое периметр многоугольника
- Свойства многоугольника
-
Как вычислить периметр правильного многоугольника
- Свойства правильного многоугольника
- Формула
-
Для неправильного многоугольника
- Описание
- Формула
-
По заданным координатам
- Как начертить многоугольник
- Формула для расчета периметра
- Примеры решения задач
Что такое периметр многоугольника
Определение
Периметр многоугольника в геометрии — это результат сложения длин всех его сторон.
Свойства многоугольника
- Все стороны прямые.
- Стороны не пересекаются (кроме звездчатых).
- Двумерная фигура.
- Сумма внешних углов всегда равна 360º.
- Сумма внутренних углов равна (frac{n(n-3)}2) (для правильных фигур).
Как вычислить периметр правильного многоугольника
Свойства правильного многоугольника
- Все стороны равны.
- Все углы равны.
- Центр равно удален ото всех вершин и сторон.
- Сумма всех углов равна 180º×(n−2).
- Все внешние углы при сложении их градусных мер дадут 360º.
- Все биссектрисы углов между сторонами равны и пересекают центр фигуры.
- Возможно вписать окружность и описать круг. Площадь кольца зависит от длины стороны многоугольника.
Формула
P=a×n
где a — длина стороны, n — количество сторон.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Для неправильного многоугольника
Описание
У неправильного многоугольника все стороны разного размера.
Формула
Его периметр (P) можно рассчитать, сложив все длины его сторон (a, b, c,d и т.д.). Это первый способ.
P=a+b+c+d+…
Второй способ: если есть стороны с одинаковыми длинами, формулу можно сократить, использовав умножение.
Пример
Дан прямоугольник со сторонами 4см, 4см, 2см и 2см. Чтобы узнать периметр, можно просто их все сложить, как показано в формуле выше. А можно сделать так: 4×2+2×2, так как стороны попарно равны.
Этот способ подойдет и для фигур с большим количеством сторон, некоторые из которых равны.
Пример
Дан восьмиугольник со сторонами 5см, 5см, 3см, 3см, 3см, 2см и 1см. Периметр можно высчитать сложением, а можно считать так: 5×2+3×3+2+1.
По заданным координатам
Как начертить многоугольник
Еще один способ вычисления периметра многоугольника – построить фигуру на координатной прямой.
Для этого нужно:
- Построить координатные оси.
- Нанести на них заданные координаты (длины) сторон. Соединить точки.
Формула для расчета периметра
Далее нужно находить длины всех получившихся сторон.
- Размеры прямых сторон легко узнавать методом подсчета координатных меток между точками сторон. Записать получившиеся значения рядом со сторонами.
- Найти длину наклонных сторон. Это можно сделать по формуле: (d=sqrt{left(x_2-x_1right)^2+left(y_2-y_1right)^2})
Примечание
В формулу нужно подставить вместо x и y координаты сторон.
3. Найти периметр сложением длин всех сторон по формуле для неправильного многоугольника: P=a+b+c+d…, где a,b,c,d… — длины сторон. А если получился правильный: P=a×n, где a – длина стороны, а n – количество сторон фигуры.
Примеры решения задач
Примечание
Задания приведены разного уровня сложности. Расположены по принципу «от простого к сложному».
Во всех задачах нужно найти периметр фигур. Этот вопрос дублироваться в каждом примере ниже не будет.
Пример 1
Дан треугольник ABC. AB=28см, BC=51см, AC=46см.
Решение
P=AB+BC+AC=28+51+46=125см
Пример 2
В прямоугольнике ABCD длина синей стороны 12 см, а красной 18 см.
Решение
AD=BC=12см
AB=CD=18см.
P=12×2+18×2=24+36=60см.
Пример 3
Дан квадрат со стороной 12 см.
Решение
Мы знаем, что все стороны квадрата одинаковые. Их всего 4. Значит, P=12×4=48см.
Пример 4
Дана фигура (данные на рисунке).
Решение
На рисунке мы видим восьмиугольник. У него шесть сторон по 10 см и две стороны по 8 см. Значит, P=10×6+8×2=60+16+76см.
Насколько полезной была для вас статья?
Рейтинг: 2.20 (Голосов: 5)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Содержание:
- Формула
- Примеры вычисления периметра многоугольника
Формула
Чтобы найти периметр многоугольника необходимо найти сумму длин всех его сторон.
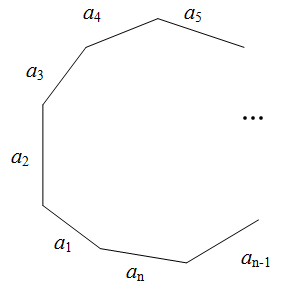
В общем случае, если задан произвольный
$n$-угольник со сторонами
$a_1, a_2, … a_{n-1}, a_n$ имеет место следующая формула для нахождения периметра этого
$n$-угольника:
$$P_{n}=a_{1}+a_{2}+ldots a_{n-1}+a_{n}=sum_{i=1}^{n} a_{i}$$
Если $n$-угольник правильный, то есть все его стороны равны
$a$, тогда его периметр вычисляется по формуле:
$$P_n=n cdot a$$
Примеры вычисления периметра многоугольника
Пример
Задание. Дан пятиугольник со сторонами
$a_1=2$, $a_2=3$,$a_3=1$,$a_4=5$,$a_5=7$. Найти его периметр.
Решение. Периметр пятиугольника найдем по формуле:
$$P_{5}=a_{1}+a_{2}+a_{3}+a_{4}+a_{5}$$
Подставляя заданные длины сторон, получим:
$P_{5}=a2+3+1+5+7=18$
Ответ. $P_{5}=18$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. В правильный шестиугольник вписана окружность радиуса $r=2 sqrt{3}$ дм. Найти периметр этого шестиугольника.
Решение. Сторона правильного шестиугольника
$a$ и радиус $r$, вписанной в него окружности, связанны
следующим соотношением:
$$r=frac{a sqrt{3}}{2}$$
Найдем из этого соотношения длину стороны:
$2 sqrt{3}=frac{a sqrt{3}}{2} Rightarrow a=frac{2 cdot 2 sqrt{3}}{sqrt{3}} Rightarrow a=4$ (дм)
Так как заданный шестиугольник правильный, то для вычисления его периметра воспользуемся формулой:
$P_{6}=6 cdot a=6 cdot 4=24$ (дм)
Ответ. $P_{6}=24$ (дм)
Читать дальше: как найти периметр.