Математика, 2 класс. Урок № 49
Периметр прямоугольника
Перечень вопросов, рассматриваемых в теме:
Изучение правила вычисления периметра прямоугольника.
Глоссарий по теме:
Прямоугольник – четырёхугольник, у которого все углы прямые.
Периметр – сумма длины всех сторон плоской фигуры.
Основная и дополнительная литература по теме урока:
1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.2/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. –
8-е изд. – М.: Просвещение, 2017. – с.16.
2. Математика. Рабочая тетрадь. 2 класс. Учебное пособие для общеобразовательных организаций. В 2 ч. Ч.2/ М. И. Моро, М.А.Бантова –
7-е изд., дораб. – М.: Просвещение, 2016. – с.22.
Открытые электронные ресурсы по теме урока:
Интересные факты о математике. Познай мир. URL:
https://knowworld.ru/fakty/interesnyie-faktyi-o-matematike/ (дата обращения: 18.08.2018)
Теоретический материал для самостоятельного изучения
Прямоугольные предметы окружают нас повсюду.



Рамки, телефоны, тетради и многое другое.
Данная фигура – прямоугольник. Вспомним, какие отличительные особенности прямоугольника мы знаем.

Прямоугольник – это четырёхугольник, у которого четыре прямых угла и стороны попарно равны.

Рассмотрим следующую задачу: «Вокруг дачного участка необходимо поставить забор. Ширина этого участка – 5 метров, длина – 10 метров. Забор какой длины получится?»
Забор ставят по границам участка, поэтому, чтобы узнать длину забора, нужно знать длину каждой из сторон.
длина
 ширина
ширина
длина
У данного прямоугольника стороны равны: 5 метров, 10 метров, 5 метров, 10 метров.
Составим выражение для подсчета длины забора. Это первый способ вычислений: 5 + 10 + 5 + 10
Воспользуемся переместительным законом сложения:
5 + 10 + 5 + 10 = 5 + 5 + 10 + 10
В данном выражении есть суммы одинаковых слагаемых
5 + 5 и 10 + 10
В этой записи рядом стоят две пары одинаковых чисел. А ведь сумму одинаковых слагаемых можно заменить умножением. Это второй способ вычислений:
5 + 5 + 10 + 10 = 5 · 2 + 10 · 2
Теперь воспользуемся распределительным законом умножения относительно сложения. Это третий способ вычислений: 5 · 2 + 10 · 2 = (5 + 10) · 2
Этот способ можно назвать рациональным, то есть, наиболее удобным и коротким, потому что в нём меньше действий, чем в предыдущих способах.
Найдём значение выражения (5 + 10) · 2
Сначала выполняем действие в скобках: 5 + 10 = 15
А затем повторяем число 15 два раза: 15 · 2 = 30.
Ответ: 30 метров забор вокруг участка.
Забор вокруг участка – это периметр этого участка. Периметр прямоугольника – сумма длин всех его сторон.
Делаем вывод: периметр прямоугольника – сумма длин всех его сторон. Чтобы найти периметр, надо измерить каждую сторону, а результаты сложить, или заменить сложение умножением как в способах номер 2 и 3.
Тренировочные задания.
1. Решите задачу: Длина листа картона 4 см. Ширина 3 см. Вычислите периметр данного листа. Запишите решение тремя способами.
Правильный ответ:
1 способ. 4+3+4+3=14 (см)
2 способ. 4 · 2+ 3·2=14 (см)
3 способ. (4+3) ·2=14 (см)
Ответ: 14 сантиметров периметр листа картона.
2. Выберите верное решение:
Длина прямоугольника 5 см, ширина 3 см. Чему равен периметр прямоугольника?
А) 8 см Б) 13 см В) 16 см
Правильный ответ В) 16 см

Пример:
измеряя с помощью линейки длины сторон прямоугольника, получим (2) см и (4) см. Противолежащие им стороны имеют такую же длину — (2) см и (4) см.
Найдём сумму длин всех сторон этого прямоугольника.
Для этого сложим все эти длины.
Получим:
(2) см (+) (4) см (+) (2) см (+) (4) см (=) (12) см.
Периметр — это сумма длин всех сторон фигуры.
Значит,
складывая длины всех сторон прямоугольника, получаем периметр прямоугольника.
Периметр обозначается заглавной латинской буквой (Р).
Итак,
периметр прямоугольника (Р = 12) см.
Найдём периметр треугольника.

Сначала измерим стороны треугольника.
Длины сторон треугольника равны (4) см, (3) см, (6) см.
Значит,
сумма длин всех сторон треугольника, т. е. периметр треугольника
равен:
(Р) (=) (3) см (+) (4) см (+) (6) см (=) (13) см.
Дан квадрат, длина стороны которого равна (4) см.

У квадрата все стороны равны.
Периметр квадрата равен сумме длин всех сторон квадрата.
Получим:
(Р) (=) (4) см (+) (4) см (+) (4) см (+) (4) см (=) (16) см.
Если у треугольника все стороны равны, такой треугольник называется равносторонний.

Для определения периметра данного треугольника найдём сумму длин всех его сторон.
Получим:
(Р) (=) (5) см (+) (5) см (+) (5) см (=) (15) см.
Источники:
Рис. 1. Прямоугольник. © ЯКласс
Рис. 2. Треугольник. © ЯКласс
Рис. 3. Квадрат. © ЯКласс
Рис. 4. Равносторонний треугольник. © ЯКласс
- Главная
- Справочники
- Справочник по математике для начальной школы
- Основы геометрии
- Периметр многоугольника
Любой многоугольник – это замкнутая ломаная линия.
Чтобы найти длину ломаной линии, нужно сложить длины ее отрезков-звеньев.
Значит, периметр многоугольника – это сумма длин всех его сторон.
В математике периметр обозначают буквой P (пэ).
Периметр прямоугольника
Например, найдём периметр данного прямоугольника.
1 способ:
Этим способом мы пользуемся до тех пор, пока не выучили действие умножение.
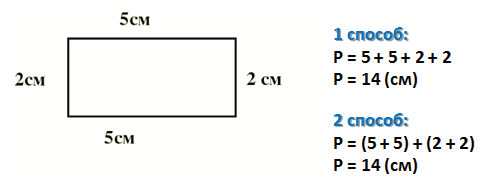
2 способ:
Мы знаем, что периметр прямоугольника – сумма длин всех его сторон.
Формула для подсчета периметра прямоугольника:
(a + b) • 2
a – длина прямоугольника
b – ширина прямоугольника.
Сумма длины и ширины (a + b) называется полупериметром, чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, то есть умножить на 2.
Воспользуемся формулой периметра прямоугольника и найдем периметр прямоугольника со сторонами 2 см и 6 см:

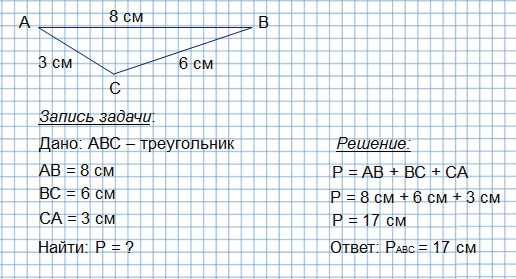
Периметр треугольника
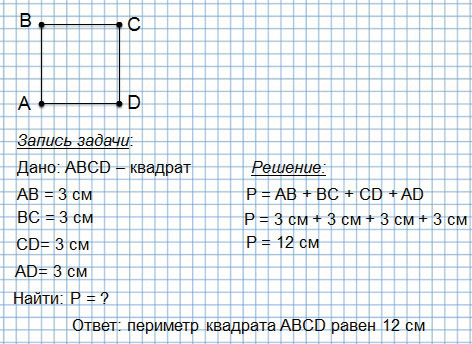
Периметр квадрата
Первый способ (когда мы еще не знаем действие умножения):
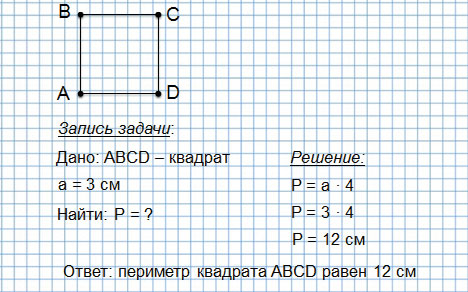
Второй способ (когда мы изучили действие умножения):
Советуем посмотреть:
Круг. Шар. Овал
Треугольники
Многоугольники
Угол. Виды углов
Обозначение геометрических фигур буквами
Площадь фигуры
Окружность
Основы геометрии
Правило встречается в следующих упражнениях:
1 класс
Страница 4. Урок 3,
Петерсон, Учебник, часть 3
Страница 5. Урок 3,
Петерсон, Учебник, часть 3
Страница 87. Урок 44,
Петерсон, Учебник, часть 3
2 класс
Страница 66,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 79,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 50,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 54. ПР 2. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 65. Тест 1. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 53. Урок 27,
Петерсон, Учебник, часть 1
Страница 59. Урок 30,
Петерсон, Учебник, часть 1
Страница 92. Урок 39,
Петерсон, Учебник, часть 2
Страница 19. Урок 6,
Петерсон, Учебник, часть 3
Страница 63. Урок 23,
Петерсон, Учебник, часть 3
3 класс
Страница 55,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 65,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 25,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 78,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 43. Тест 1. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 23. Урок 10,
Петерсон, Учебник, часть 2
Страница 39. Урок 15,
Петерсон, Учебник, часть 2
Страница 87. Урок 38,
Петерсон, Учебник, часть 2
Страница 15. Урок 7,
Петерсон, Учебник, часть 3
Страница 24. Урок 11,
Петерсон, Учебник, часть 3
4 класс
Страница 18,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 23,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 26,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 26,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 32,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 56,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 4,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 97,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 19,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 66,
Моро, Волкова, Рабочая тетрадь, часть 2
5 класс
Задание 207,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 208,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 209,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 210,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 211,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
6 класс
Задание 389,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 428,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 430,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Периметр прямоугольника
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы расскажем, что такое периметр прямоугольника и по каким формулам его можно посчитать.
Тема в общем-то простая, каждый из нас изучал ее еще в начальных классах. Тем не менее с возрастом кто-то мог что-нибудь и подзабыть.

Но для начала предлагаем освежить теоретическую базу и вспомнить, что такое прямоугольник.
Что такое прямоугольник и что такое периметр
Прямоугольник – это геометрическая фигура, которая представляет собой четырехугольник, а конкретно параллелограмм (фигура, у которой противоположные стороны равны и параллельны). Но параллелограмм не обычный, а с особенностями. У него все стороны пересекаются друг с другом под прямым углом.
Выглядит прямоугольник соответственно:

А частным случаем прямоугольника является квадрат:

У такого прямоугольника стороны не только пересекаются под прямым углом, но и равны между собой.
Как и многие термины в математике, жир слово пришло к нам из Древней Греции. Дословно оно означает «περιμετρέο» — «окружность» или «измерять вокруг». Таким образом,
Периметр – это совокупная длина границ любой геометрической фигуры. Этим словом обозначают как сами границы, так и их математическое значение.
С этим словом мы часто встречаемся в повседневной жизни. Например, когда нужно поставить забор на дачном участке, то его устанавливают по периметру участка. И мы понимаем, что речь идет о границах.
Также, солдаты или полицейские часто стоят в оцеплении «по периметру» какой-то территории. А кулинары часто украшают торт фруктами или кремовыми цветами также «по периметру».
Как найти периметр прямоугольника
Возьмем для примера такой прямоугольник:
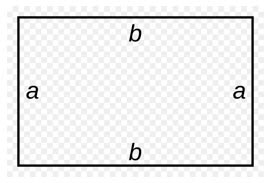
Исходя из общего определения, чтобы посчитать периметр прямоугольника, надо просто сложить все его стороны.
Периметр в математике обозначается латинской буквой «Р». И соответственно формула выглядит так:
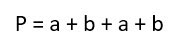
С учетом равенства сторон, формулы можно существенно упростить:
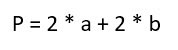
или
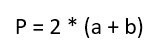

Предположим, что у нас длина прямоугольника равна 4 сантиметрам, а ширина 2. Тогда периметр этой геометрической фигуры составит:
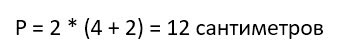
И тут появляется важное замечание. Периметр измеряется в тех же величинах, что и длины сторон прямоугольника. Это могут быть миллиметры, сантиметры, метры, километры и так далее.
В случае с квадратом, который, напомним, является частным случаем прямоугольника, посчитать периметр еще проще. Благодаря тому, что у него все стороны равны (назовем их условно «а»), формула выглядит так:
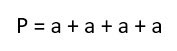
или
![]()
Опять же приведем конкретный пример. Если возьмем квадрат со стороной 4 сантиметра, то его периметр составит P = 4 * 4 = 16 сантиметров.
Другие формулы для расчета периметра прямоугольника
Иногда школьникам предлагают такую задачу – нужно вычислить периметр прямоугольника, зная его площадь и длину одной стороны.
Тут надо знать, как вычисляется сама площадь. Для этого надо просто перемножить длины двух сторон:
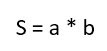
Соответственно, мы можем определить длину недостающей нам стороны. Для этого надо просто разделить площадь на другую сторону:
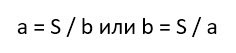
Таким образом, мы у нас будут значения обеих сторон прямоугольника. А уже после периметр вычисляется по стандартной формуле.
Бывают и более сложные задачи по нахождению периметра прямоугольники, например, как в приведенном ниже видео:
Вместо заключения
Зная длины сторон, можно вычислять и периметры более сложных прямоугольных фигур. Вот таких:
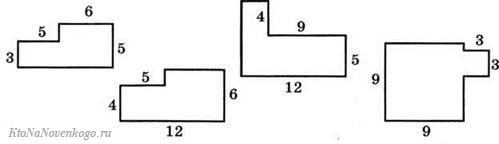
Страшно выглядят они только на первый взгляд. А на деле, надо просто провести недостающую линию и разделить каждую из фигур на два прямоугольника. Далее вычисляем их по отдельности и складываем друг с другом. Как результат – общий периметр фигуры.
Вот и все, что мы хотели сегодня рассказать.
Открытый урок математики. 2 класс
Тема: Периметр прямоугольника
Педагогическая цель: обобщить, систематизировать, открыть новые знания о прямоугольнике, о нахождении периметра этой фигуры по формуле.
Тип, вид урока: комбинированный
Планируемые результаты:
Предметные: вычислять периметр прямоугольника; – формулировать правило нахождения периметра прямоугольника по формуле; – решать задачи на нахождение периметра прямоугольника; – анализировать ситуацию; -выполнять учебное задание в соответствии с целью; -осуществлять взаимопроверку и самооценку при выполнении учебного задания; -формулировать собственное мнение и позицию; – учитывать разны мнения и стремиться к сотрудничеству в рамках учебного диалога.
Метапредметные.
Регулятивные: принимать и сохранять учебную задачу, планировать свое действие в соответствии с поставленной задачей и условиями ее реализации, уметь оценивать результат своей работе на уроке.
Познавательные: научатся понимать заданный вопрос, в соответствии с ним строить ответ в устной форме; осуществлять поиск необходимой информации в разных источниках; получат возможность научиться: ориентироваться на возможное разнообразие способов решения учебной задачи.
Коммуникативные: уметь участвовать в диалоге на уроке и в жизненных ситуациях (вслух говорит один, а другие внимательно слушают); отвечать на вопросы учителя, товарищей по классу; соблюдать простейшие нормы речевого этикета: здороваться, прощаться, благодарить; осуществлять работу в паре и в группе.
Личностные: развивать навыки сотрудничества со взрослыми и сверстниками в разных социальных ситуациях.
|
Технология проведения |
Деятельность учителя |
Деятельность учащихся |
Планируемые результаты |
|
I. Мотивация к учебной деятельности (3 мин) Цель: создание психологического комфорта (для создания ситуации успеха) Включение учащихся в деятельность на личностно- значимом уровне. |
– Наш урок математики я хочу начать со стихотворения. Нетрудно, ребята, нам песенку спеть, Нетрудно, а всё таки надо уметь. За что ни возьмись, нужно мастером стать И дело любое уметь выполнять! Сломалась игрушка – умей починить, А новую сам научись смастерить, Не даром ребята смекалка дана, Во всём и везде помогает она. Умей, если нужно, заштопать чулок, Без помощи свой приготовить урок, Будь первым в ученье, будь первым в труде, У нас белоручек не любят нигде. – О чём это стихотворение? – О труде и об отношении к труду русский народ создал много пословиц. Одна из пословиц послужит нам девизом на сегодняшнем уроке Где охота и труд, там поля цветут. – Итак, начинаем трудиться. Мы друг другу улыбнёмся. И за дело все возьмёмся. Чтобы объективно оценить ваш труд, вы будете работать с оценочными листами. (Учитель знакомит с критериями оценки) |
Слушают стихотворение, отвечают на вопрос учителя: – (О труде, об отношении к труду) Дети объясняют значение пословицы |
Уметь совместно договариваться о правилах поведения и общения в школе и следовать им (Коммуникативные УУД). Уметь оформлять свои мысли в устной форме (Коммуникативные УУД). Самооценка |
|
II. Актуализация опорных знаний и решение новой задачи. (7 минут) Цель: организует выполнение учащимися пробного учебного действия; – организовать фиксирования учащимися индивидуального затруднения |
Математический диктант:
11) Задумали число. От этого числа отняли 34 и получили 40. Какое число задумали? 12) Какое число увеличили на 5, если получили 43? 13) Сколько получится, если по 5 взять 3 раза? ( Ответы: 79, 16, 39, 34, 32, 23, 40, 10, 53, 20, 74, 48, 15). Оцените свою работу. |
Учащиеся записывают только ответы, проверяют по ключу на доске, оценивают свою работу. |
Уметь преобразовывать информацию из одной формы в другую (Познавательные УУД). Уметь оформлять свои мысли в устной форме (Коммуникативное УУД) Уметь ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя (Познавательные УУД). Умение слушать и понимать речь других (Коммуникативные УУД) Самооценка |
|
III. Постановка учебной задачи (3 мин) Цель: проговаривание темы и цели урока. |
|
Дети располагают числа в порядке возрастания, переворачивают их обратной стороной. У них должно получиться слово: ПРЯМОУГОЛЬНИК |
Уметь формулировать мысли в устной и письменной форме |
|
IV. Открытие нового знания (7 мин) Цель: решение устной задачи и обсуждение проекта её решения |
– Внимательно посмотрите на доску, среди этих фигур найдите прямоугольник. – Какие отличительные особенности прямоугольника вам уже известны? – А что в нашей жизни может иметь прямоугольную форму? (Книга, крышка стола, земельный участок) Задача: Вокруг одного земельного участка строителям понадобилось поставить забор. Ширина этого прямоугольного участка 5 метров, а длина 10 метров. Строителям нужно было узнать, забор какой длины у них получится. Забор ставят по границам участка, поэтому для того, чтобы узнать длину забора, надо знать длину каждой из сторон. Ширина равна пяти метрам, длина десяти метрам и такая же сторона есть ещё одна пять метров, и сторона 10 метров. Давайте запишем выражением. Решение: 5+10+5+10 Узная значение этого выражения, можно узнать длину забора. Внимательно посмотрите на выражение, что интересного вы заметили? Воспользовавшись переместительным свойством сложения мы можем переставить слагаемые. 5+5+10+10 Ещё раз внимательно посмотрите на это выражение. Мы видим, что у нас есть сумма одинаковых слагаемых. Сумму одинаковых слагаемых можно заменить умножением. Давайте это и сделаем. Сначала слагаемое 5 у нас повторяется 2 раза. Каким выражением это можно заменить? (Пять повторяется два раза значит 5*2) И суммы слагаемых, каждое из которых равно 10 повторяется тоже два раза, давайте произведём замену 10*2. Посмотрите внимательно, какое выражение у нас получилось. 5*2+10*2 – А теперь давайте воспользуемся распределительным законом умножения относительно сложения и узнаем длину забора. Вот какое выражение у нас получилось. (5+10)*2 Давайте найдём его значение. Сначала выполняем действие в скобках и узнаем сумму чисел 5 и 10, она равна 15. Дальше повторяем число 15 два раза и узнаём, что длина забора равна 30 метрам. (5+10)*2=30(м) Оказывается, для того, чтобы узнать длину забора, нам потребовалось сложить длину всех четырёх сторон прямоугольника и мы нашли сумму длин сторон прямоугольника. А сумма длин сторон любой фигуры называется периметром Ответ: периметр прямоугольника – 30 м. Есть специальная формула для нахождения периметра прямоугольника, давайте с ней познакомимся. Посмотрите на доску, здесь в общем виде изображена формула для нахождения длин сторон прямоугольника. Посмотрите внимательно: (a+b)*2 а – длина b – ширина (a+b) – полупериметр Буковка а обозначает длину этого прямоугольника, буковка b обозначает ширину прямоугольника, сумма одной длины и одной ширины называется полупериметром. Для того чтобы из полупериметра получить периметр, нужно полупериметр умножить на 2. |
Из множества фигур дети находят прямоугольник, формулируют определение: прямоугольник – это четырёхугольник, у которого четыре прямых угла и стороны попарно равны. Решают задачу, записывая все шаги в тетрадях |
Уметь проговаривать последовательность действий на уроке; уметь доб ы вать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке (Познавательные УУД) Уметь оформлять свои мысли в устной форме; слушать и понимать речь других (Коммуникативные УУД). Уметь работать по коллективно составленному плану (Регулятивные УУД) |
|
V. Первичное закрепление с проговариванием во внешней речи (3 мин) Цель: – организовать усвоение учениками нового способа действий с проговариванием во внешней речи |
– Давайте воспользуемся этой формулой и найдём периметр другого прямоугольника со сторонами 7 см и 3 см – Подставляем в формулу значения длин сторон второго прямоугольника. (7+3)*2 Длина прямоугольника это 7 см, его ширина 3 см. Находим сумму длины и ширины – это 10 см. И умножаем на 2. Узнаём, что периметр нашего прямоугольника равен 20 см. Периметр любой фигуры измеряется в линейных единицах (см, дм, м) Что вы сейчас узнали? – Правильно. Вы узнали формулу для вычисления периметра прямоугольника. Используйте её всякий раз, когда вам нужно узнать периметр прямоугольника. |
Дети с проговариванием решают новую задачу на нахождение периметра прямоугольника |
Уметь проговаривать последовательность действий на уроке (Регулятивные УУД). Уметь оформлять свои мысли в устной и письменной форме; слушать и понимать речь других (Коммуникативные УУД) |
|
VI. Самостоятел ьная работа с самопроверк ой по эталону (7 мин) Цели: – организовать выполнение учащимися самостоятельной работы на новое знание; – организовать самопроверку по эталону, самооценку; организовать выявление места и причины затруднений, работу над ошибками. |
Попробуйте самостоятельно найти периметр прямоугольника в задании № 2 на стр. 52 учебника. Проверьте работу и оцените. |
Учащиеся самостоятельно выполняют задание № 2 стр. 52 учебника. Выполняют самопроверку по эталону. Выполняют самооценку по алгоритму |
Уметь проговаривать последовательность действий на уроке (Регулятивные УУД). Уметь выполнять работу по предложенному плану (Регулятивные УУД). Уметь вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок (Регулятивные УУД). Способность к самооценке на основе критерия успешности учебной деятельности (Личностные УУД) |
|
VII. Включение нового в систему знаний и повторение (7 мин) Цель: зафиксировать новое содержание урока |
– Расположите прямоугольники в порядке уменьшения их периметра (задание из электронного приложения к учебнику) |
Располагают прямоугольники в порядке уменьшения их периметра. Выполняют самопроверку по эталону. Выполняют самооценку по алгоритму. |
|
|
VIII. Рефлексия учебной деятельности на уроке (3 мин) Цель: организовать рефлексию и самооценку учениками собственной учебной деятельности |
– Молодцы, ребята, я вами очень довольна. В конце нашего урока подсчитайте общее количество баллов. Оцените свой труд по алгоритму: 15-14 баллов – отметка «5» 13-11 баллов – отметка «4» 10-8 баллов – отметка «3» 7 баллов и меньше – отметка «2» – А теперь подумайте и продолжите утверждения: Сегодня на уроке я узнал… Самыми лёгкими заданиями для меня были… Трудными для меня оказались задания… |
Подсчитывают баллы, выставляют отметки. Организуют рефлексию |
Уметь проговаривать последовательность действий на уроке (Регулятивные УУД). Уметь оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки. (Регулятивные УУД). Способность к самооценке на основе критерия успешности учебной деятельности (Личностные УУД |
Оценочный лист
Ученика ___________________________________________________
Класс _____________________________________________________
|
Выполнил всё правильно (5 баллов) |
Выполнил правильно, но с некоторыми недочётами (4 балла) |
При выполнении допустил ошибки (3 балла) |
При выполнении допустил много ошибок или не выполнил вообще (2 балла) |
|
|
Математический диктант |
||||
|
Нахождение периметра прямоугольника по формуле |
||||
|
Расположить прямоугольники в порядке уменьшения периметра |
||||
|
Итого: |
баллов – отметка – |
