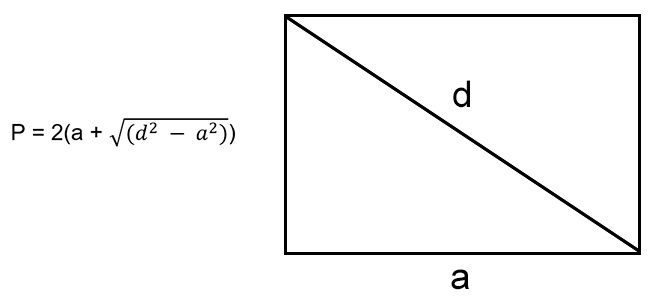как вычислить периметр прямоугольника если известна площадь и высота.
Николай Осипов
Ученик
(231),
на голосовании
10 лет назад
Дополнен 10 лет назад
Спасибо!
Голосование за лучший ответ
Константин Сорокин
Мыслитель
(5637)
10 лет назад
Периметр прямоугольника равен сумме его сторон умноженной на два, высотой в прямоугольнике является одна из его сторон, площадь прямоугольника равна произведению его сторон. В данном случае делим площадь на высоту, находим вторую сторону и вычисляем периметр.
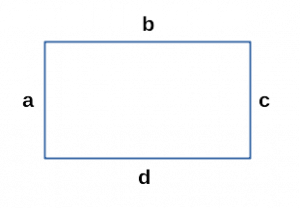
Периметр прямоугольника
Периметр прямоугольника — это сумма
всех сторон прямоугольника.
Периметр прямоугольника можно рассчитать
через четыре стороны, через смежные стороны,
через диагональ, через площадь,
через радиус описанной окружности.
Самый простой способ найти периметр
прямоугольника, это сложить все стороны.
Также, исходя из свойства прямоугольника, — «противоположные
стороны равны и параллельны», можно сказать, что периметр
численно равен удвоенной сумме ширины и высоты — двух
смежных сторон прямоугольника.
Кроме этих двух способов периметр прямоугольника
можно найти через другие величины. Например, через
площадь прямоугольника, диагональ прямоугольника, и так далее.
В прямоугольник невозможно вписать окружность,
поэтому выразить периметр через вписанную
окружность не получится.
Единицы измерения периметра прямоугольника:
км, м, дм, см, мм.
Формулы периметра прямоугольника
- Периметр прямоугольника через четыре стороны
Полупериметр
Полупериметр — это половина периметра.
Обозначается латинской буквой p.
Чтобы найти полупериметр нужно разделить
периметр на два, или домножить периметр на 0.5.
[ p = frac
= P cdot 0.5 ]
Полупериметр применяется в некоторых формулах
нахождения разных величин прямоугольника. Вместо того,
чтобы вычислять периметр, в таких формулах
удобней вычислять полупериметр.
Основные определения и величины
Длина прямоугольника — это длинная сторона
/ наибольшая сторона прямоугольника.
Обозначается латинской буквой a.
Ширина прямоугольника — это широкая сторона
/ наименьшая сторона прямоугольника.
Обозначается латинской буквой b.
Сторона прямоугольника — это ширина или длина прямоугольника,
в зависимости от численного значения длины стороны.
Обозначается латинской буквой a или b.
Диагональ прямоугольника — это отрезок, соединяющий
противоположные стороны прямоугольника.
Обозначается латинской буквой c или d.
Средняя линия прямоугольника — это отрезок, соединяющий
наименьшие параллельные стороны прямоугольника друг с
другом, причем делящий их пополам на равные отрезки.
Обозначается латинской буквой l.
Радиус описанной окружности прямоугольника — это отрезок,
соединяющий центр описанной около треугольника
окружности и произвольную точку на окружности.
Обозначается латинской буквой R.
Высота прямоугольника — это любая сторона прямоугольника,
а также любой отрезок в прямоугольнике, образующий угол в 90 градусов.
Как вычислить площадь и периметр прямоугольника
В создании этой статьи участвовала наша опытная команда редакторов и исследователей, которые проверили ее на точность и полноту.
Команда контент-менеджеров wikiHow тщательно следит за работой редакторов, чтобы гарантировать соответствие каждой статьи нашим высоким стандартам качества.
Количество просмотров этой статьи: 15 252.
Прямоугольник — это четырехугольник (двумерная фигура) с четырьмя прямыми углами. Параллельные стороны прямоугольника равны. [1] X Источник информации Прямоугольник, у которого все стороны равны, называется квадратом. Все квадраты являются прямоугольниками, но не все прямоугольники — квадраты. Периметр фигуры равен сумме значений ее сторон. [2] X Источник информации Площадь фигуры равна произведению ее длины на ширину. [3] X Источник информации
Как найти периметр прямоугольника
Прямоугольник — это четырехугольник, у которого все четыре угла прямые, то есть, составляют 90 градусов. Частным случаем прямоугольника могут быть квадрат или ромб.
Периметр прямоугольника — это сумма длин всех его ребер.
Основные свойства прямоугольника:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- противоположные стороны фигуры равны и параллельны друг другу;
- сумма всех углов равна 360 градусов;
- диагонали прямоугольника равны по длине и точкой пересечения делятся пополам;
- диагонали делят фигуру на два одинаковых прямоугольных треугольника;
- по теореме Пифагора, квадрат диагонали прямоугольника равен сумме квадратов двух его соседних ребер;
- стороны рассматриваемого четырехугольника также являются его высотами;
- точка пересечения диагоналей — это центр прямоугольника и также центр вписанной окружности;
- диагональ этого четырехугольника — это диаметр описанной окружности;
- вокруг него всегда можно описать окружность.
Варианты нахождения периметра прямоугольника
По сторонам
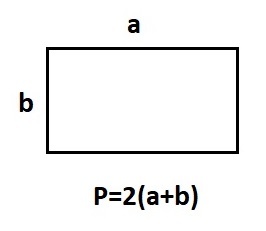
Если нам известны все стороны прямоугольника (или две смежные), мы можем использовать следующую формулу для нахождения суммы длин всех ребер:
где (a) и (b) — это две соседние стороны фигуры.
По любой стороне и площади
Зная значение любого из ребер четырехугольника и его площадь, мы можем найти значение второго и периметр фигуры.
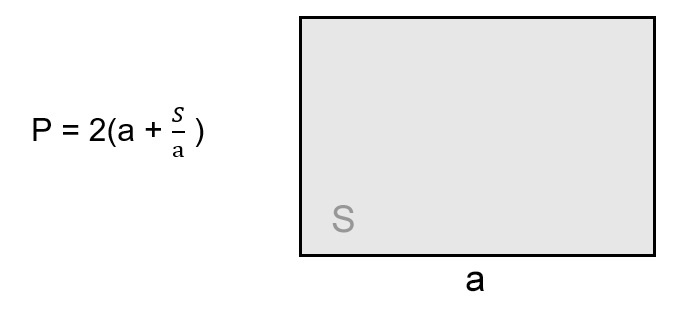
Так как площадь прямоугольника — это произведение двух его смежных сторон ((S=atimes b)) , чтобы найти неизвестную сторону, нужно поделить площадь на известную величину: (b=frac Sa) .
Получается, что формула для расчета (P) рассматриваемой фигуры будет выглядеть следующим образом:
По любой стороне и диагонали
В случае, если мы знаем длину одного из ребер и диагональ данного четырехугольника, мы можем найти вторую сторону с помощью теоремы Пифагора.
где (d) — диагональ прямоугольника, а (b) — неизвестная сторона.
Чтобы рассчитать сумму длин всех сторон, нужно воспользоваться формулой:
По любой стороне и радиусу описанной окружности
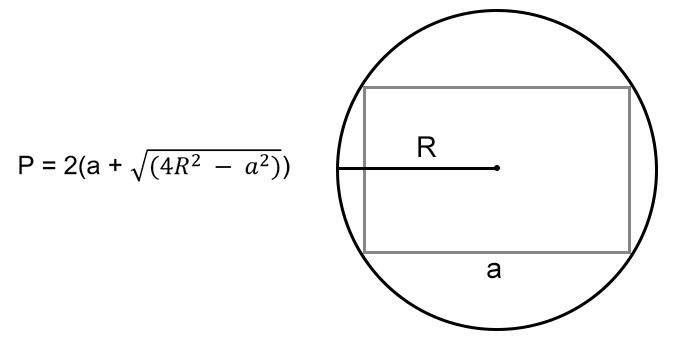
Когда нам известна одна из сторон и радиус описанной окружности вокруг прямоугольника, мы можем узнать его неизвестное ребро. Из свойств прямоугольника помним, что точка пересечения диагоналей фигуры — это центр описанной окружности. Это значит, что 1/2 диагонали — это радиус этой окружности. Таким образом, по теореме Пифагора мы можем узнать неизвестную сторону прямоугольника:
где (R) — радиус описанной окружности.
Тогда формула для расчета P будет выглядеть так:
Примеры решения задач
Задача 1
Известно, что стороны прямоугольника равны 5 см и 7 см. Найти его периметр.
Решение:
Применяем самую первую формулу для расчета:
Задача 2
Мы знаем, что площадь четырехугольника с прямыми углами составляет 24 (см^2) , одна из его сторон равна 6 см. Вычислить Р фигуры.
Решение:
Берем формулу (P=2(frac Sa+a)) и подставляем известные значения:
Задача 3
Дан прямоугольник со стороной 3 см и диагональю 5 см. Нужно высчитать P данной фигуры.
Решение:
Вспоминаем формулу для расчета (P=2(a+sqrt)) и вставляем известные величины:
Задача 4
Вокруг прямоугольника с ребром 3 см описали окружность с радиусом 5 см. Определить P заданной фигуры.
Решение:
В этом случае для расчета суммы длин всех сторон применяем формулу (P=2(a+sqrt)) . Используем известные значения и получаем:
Как найти периметр прямоугольника
Вас ждут четыре простых способа.
Напомним, периметром называют суммарную длину всех сторон. Вычислить её можно по‑разному. Выбирайте формулу в зависимости от известных вам данных.
Зная все или две соседние стороны
Для полноты упомянем простейшие классические формулы.
- Если известна длина всех сторон прямоугольника, просто посчитайте сумму этих величин.
- Если вы знаете только две соседние стороны, суммируйте их и умножьте результат на два.
- P — искомый периметр;
- a, b, c, d — стороны прямоугольника.
Зная любую сторону и площадь
- Поделите площадь на длину известной стороны.
- Прибавьте результат к известной стороне.
- Умножьте полученное число на два.
- P — искомый периметр прямоугольника;
- a — известная сторона;
- S — площадь прямоугольника.
Зная любую сторону и диагональ
- Посчитайте разность квадратов диагонали и стороны.
- Найдите корень из результата.
- Прибавьте полученное число к известной стороне.
- Умножьте результат на два.
- P — искомый периметр прямоугольника;
- a — известная сторона;
- d — диагональ прямоугольника.
Зная одну любую сторону и радиус описанной окружности
- Умножьте квадрат радиуса на четыре.
- Посчитайте разность полученного числа и квадрата известной стороны.
- Найдите корень из результата.
- Прибавьте полученное число к известной стороне.
- Умножьте результат на два.
- P — искомый периметр прямоугольника;
- a — известная сторона;
- R — радиус окружности, описанной вокруг прямоугольника.
Читайте также 📐✂️📌
- Как научить ребёнка считать играючи
- Как перевести обычную дробь в десятичную
- 6 способов посчитать проценты от суммы с калькулятором и без
- 9 логических задач, которые по зубам только настоящим интеллектуалам
- 11 книг, которые прокачают математическое мышление
Свойства прямоугольника
Перечислим некоторые свойства прямоугольника:
- Все углы прямоугольника прямые.
- Противоположные стороны прямоугольника равны и параллельны.
- Диагонали прямоугольника равны и точкой пересечения делятся пополам.
Разберем задачу на нахождение периметра прямоугольника.
В прямоугольнике длина a составляет 18 см, а ширина b — 12 см. Чему равен периметр прямоугольника?
Решение
a=18a=18a=18 b=12b=12b=12
Воспользуемся формулой нахождения периметра прямоугольника и подставим вместо aaa и bbb их численные значения: P=2⋅(a+b)=2⋅(18+12)=2⋅30=60P=2cdot (a+b)=2cdot (18+12)=2cdot 30=60P=2⋅(a+b)=2⋅(18+12)=2⋅3=6 см.
Ответ: 60 см.
Ищете, где заказать заказать контрольную работу недорого онлайн? Обратитесь к профильным экспертам на Студворк!
Видео
Нахождение периметра через площадь и одну сторону
При более близком знакомстве с прямоугольником, способы нахождения его периметра начинают варьироваться в зависимости от исходных данных в задаче.

Если известны одна из сторон и площадь, то, чтобы узнать, чему равен периметр, выражается неизвестная сторона, а затем она подставляется в формулу.
Так как
S = a * b,
то

то есть, соотношение площади и периметра при известной стороне есть

Как найти площадь прямоугольника
Формула площади прямоугольника S= a*b
Если в условии известна длина одной стороны и длина диагонали, то площадь найти можно, используя в таких задачах, теорему Пифагора, она позволяет найти длину стороны прямоугольного треугольника если известны длины двух других сторон.
- Теорема Пифагора: a2 + b2 = c2, где a и b – стороны треугольника, а с – гипотенуза, самая длинная сторона.
Помни!
- Все квадраты – прямоугольники, но не все прямоугольники – квадраты. Так как:
- Прямоугольник — это четырехугольник со всеми прямыми углами.
- Квадрат — прямоугольник, у которого все стороны равны.
- Если ты находишь площадь, ответ всегда будет в квадратных единицах (мм2, см2, м2, км2 и т.д.)
Смотри также: Основные формулы по математике
Решай задание 8 по математике база с ответами
Теги
Информация по назначению калькулятора
Прямоугольник – это двумерная геометрическая фигура, имеющая 4 стороны и 4 угла. Две его стороны сходятся под прямым углом. Таким образом, прямоугольник имеет 4 угла, каждый из которых равен 90 градусов. Противоположные стороны прямоугольника имеют одинаковую длину и параллельны. Две стороны называются параллельными, когда расстояние между ними остается одинаковым во всех точках.
Поскольку все углы прямоугольника равны, его можно назвать равноугольным четырехугольником.
Некоторые свойства прямоугольника отмечены далее:
⇒ Прямоугольник – это четырехугольник.
⇒ Противоположные стороны прямоугольника равны и параллельны друг другу.
⇒ Внутренний угол прямоугольника в каждой вершине равен 90°.
⇒ Сумма всех внутренних углов равна 360°.
⇒ Диагонали делят пополам друг друга.
⇒ Длина диагоналей равна.
⇒ Поскольку стороны прямоугольника параллельны, его также называют параллелограммом.
⇒ Все прямоугольники являются параллелограммами, но не все параллелограммы являются прямоугольниками.
Онлайн калькулятор поможет найти параметры прямоугольника, такие как:
- Длины сторон
- Периметр
- Площадь
- Диагонали
- Углы
- Радиус Описанной окружности
- Диаметр Описанной окружности
- Длина Описанной окружности
- Площадь Описанной окружности
– равен сумме всех 4х сторон (P=AB+BC+CD+DA)
– равна произведению двух сторон (S=AB*BC)
– Диагональ разрезает прямоугольник на 2 прямоугольных треугольника, в которых диагональ образует гипотенузу, а две смежные стороны прямоугольника образуют две другие стороны треугольника.(AC=√(AB2 + BC2))
– всегда равны 90 градусов
Диаметр описанной окружности прямоугольника равен длине его диагонали