Цель урока: продолжить формирование
навыков работы с электронными таблицами.
Задачи:
- обучающие: формировать умения создания,
редактирования, форматирования и выполнения
простейших вычислений в электронных таблицах. - развивающие: расширить представления
учащихся о возможных сферах применения
электронных таблиц; развивать навыки
аналитического мышления, речи и внимания. - воспитательные: формировать и воспитывать
познавательный интерес; прививать навыки
самостоятельности в работе.
План урока.
- Организационный момент.
- Актуализация знаний учащихся.
- Проверка домашнего задания.
- Решение задач.
- Самостоятельное решение задачи.
- Подведение итогов. Оценки.
- Домашнее задание.
Ход урока
1. Организационный момент.
Сообщить тему урока, сформулировать цели и
задачи урока.
Сегодня мы вновь окажемся в гостях у маленького
великана Васи в Сказочной стране. Ему, как всегда,
требуется ваша помощь, ребята.
Сможете ли вы помочь Васе? Сейчас проверим!
2. Актуализация знаний учащихся.
1) Устно ответить на вопросы.
| A | B | C | D | |
| 1 | 2 | 1 | =A1+3*B1 | =A1^2+B1 |
| 2 | 4 | 6 | =A2+3*B2 | =A2^2+B2 |
- Что такое электронная таблица?
- Какие основные элементы электронной таблицы
вам известны? - Как задается имя ячейки (строки, столбца) в
электронной таблице? - Что может быть содержимым ячейки?
- Число 1 находится в столбце …, в строке …, в
ячейке с адресом … - Число 4 находится в ячейке с адресом …
- Каковы правила записи формул в ячейках?
- Чему равно значение, вычисляемое по формуле, в
ячейке С1? - Чему равно значение, вычисляемое по формуле, в
ячейке D2?
2) Какой результат будет получен в ячейках с
формулами?
| А | В | |
| 1 | 25 | 4 |
| 2 | 2 | =A1*B1/2 |
| 3 |
Ответ: 25*4/2=50
| A | B | C | D | |
| 1 | 5 | 2 | 1 | |
| 2 | 6 | 8 | 3 | |
| 3 | 8 | 3 | 4 | |
| 4 | =СУММ(B1:D3) |
- Что означает запись =СУММ(В1:D3)?
- Сколько элементов содержит блок В1:D3? Ответ: 9.
- Содержимое ячейки D3? Ответ: 5+2+1+6+8+3+8+3+4= 40
3) Проверка домашнего задания
Результаты соревнований по плаванию
Один ученик рассказывает, как он выполнил
домашнее задание (через проектор).
| № | Ф.И.О. | 1 | 2 | 3 | Лучшее время | Среднее время | Отклонение |
| 1 | Лягушкин | 3.23 | 3.44 | 3.30 | |||
| 2 | Моржов | 3.21 | 3.22 | 3.24 | |||
| 3 | Акулов | 3.17 | 3.16 | 3.18 | |||
| 4 | Рыбин | 3.24 | 3.20 | 3.18 | |||
| 5 | Черепахин | 3.56 | 3.44 | 3.52 | |||
| Лучший результат соревнований |
|||||||
| Среднее время участников соревнований |
|||||||
| Максимальное отклонение |
- Среднее время для каждого спортсмена находится
как среднее арифметическое трех его заплывов. - В ячейку “Лучшее время” записывается
минимальный результат из 3 заплывов. - В ячейку “Лучший результат соревнований”
записывается минимальное время из столбца. - В столбец “Отклонение” записывается
разность между лучшим временем спортсмена и
лучшим результатом соревнований. - В ячейку “Максимальное отклонение”
записывается максимальное значение столбца.
| Результаты соревнований по плаванию |
|||||||
| № | Ф.И.О. | 1 | 2 | 3 | Лучшее время | Среднее время | Отклонение |
| 1 | Лягушкин | 3,23 | 3,44 | 3,30 | 3,23 | 3,32 | 0,07 |
| 2 | Моржов | 3,21 | 3,22 | 3,24 | 3,21 | 3,22 | 0,05 |
| 3 | Акулов | 3,17 | 3,16 | 3,18 | 3,16 | 3,17 | 0,00 |
| 4 | Рыбин | 3,24 | 3,20 | 3,18 | 3,18 | 3,21 | 0,02 |
| 5 | Черепахин | 3,56 | 3,44 | 3,52 | 3,44 | 3,51 | 0,28 |
| Лучший результат соревнований |
3,16 | ||||||
| Среднее время участников соревнований |
3,29 | ||||||
| Максимальное отклонение | 0,28 |
4) Решение простых задач.
Маленький великан Вася решил отремонтировать
забор вокруг своего огорода и вскопать его под
посадку овощей (наступила очередная весна),
разметить грядки прямоугольной формы. Для работы
ему потребовалось найти длину забора и площадь
участка. Но ведь в школе он никогда не учился.
Поможем Васе.
№ 1. Вычислить периметр и площадь
прямоугольника со сторонами:
а) 3 и 5; б) 6 и 8; в) 10 и 7.
Эту задачу обсуждаем совместно с детьми:
- Как оформить таблицу?
- Какие формулы использовать?
- Как использовать уже записанные формулы для
следующего прямоугольника?
Оформление таблицы – на доске и в тетрадях.
В то же время другой ученик самостоятельно
решает следующую задачу и представляет свое
решение учащимся (через проектор).
№ 2. Маленький великан Вася решил
подсчитать, через сколько дней в его копилке
будет 100 руб., если ежедневно он стал класть туда
на 5 руб. больше, чем в предыдущий день. Помогите
Васе. Сейчас в его копилке 2,02 руб.
Обсудив решение задачи № 2, переходим к решению
следующей.
Один ученик показывает, как работать с
формулами, другой – как использовать функцию
суммирования, числовой формат (общий, денежный) и
т.д. (Таблица уже готова, ученикам предстоит
ввести формулы, использовать суммирование и
получить ответ).
№ 3. Посчитайте, используя ЭТ, хватит ли
Васе 150 рублей, чтобы купить все продукты, которые
ему заказала мама, и хватит ли на чипсы за 10
рублей? Сдачу мама разрешила положить в копилку.
Сколько рублей попадет в копилку?
Предполагаемое решение:
| № | Наименование | Цена в рублях | Количество | Стоимость |
| 1 | Хлеб | 9,6 | 2 | =C2*D2 |
| 2 | Кофе | 2,5 | 5 | =C3*D3 |
| 3 | Молоко | 13,8 | 2 | =C4*D4 |
| 4 | Пельмени | 51,3 | 1 | =C5*D5 |
|
Итого: |
=СУММ(E2:E5) | |||
| После покупок останется | =150-E6 | |||
| После покупки чипсов останется |
=D7-10 |
5) Самостоятельное решение задачи.
Маленький великан Вася часто бывал в гостях у
жителей Цветочного города.
Собираясь на пляж, веселые человечки решили
запастись прохладительными напитками. Незнайка
взял с собой 2 литра кваса, 1 литр газировки и 1
литр малинового сиропа, Пончик – 3 литра
газировки и 2 литра малинового сиропа, Торопыжка
– 2 литра газировки, доктор Пилюлькин – 1 литр
кваса и 1 литр касторки.
- Сколько литров напитков каждого вида взяли все
человечки вместе? - Сколько всего литров напитков взял с собой
каждый из человечков? - Сколько всего литров напитков взяли все
человечки вместе?
Оформите таблицу произвольно и сохраните в
своей личной папке.
Результат работы.
| Веселые человечки. Напитки. |
|||||
| Напиток | Незнайка | Пончик | Торопыжка | Пилюлькин | Всего |
| Квас, л | 2 | 0 | 0 | 1 | 3 |
| Газировка, л | 1 | 3 | 2 | 0 | 6 |
| Сироп, л | 1 | 2 | 0 | 0 | 9 |
| Касторка, л | 0 | 0 | 0 | 1 | 1 |
| ИТОГО: | 4 | 5 | 2 | 2 | 13 |
7) Подведение итогов. Оценки.
8) Домашнее задание.
Подумайте и решите эту задачу, если известны
еще следующие величины.
Как изменится таблица? Какие формулы появятся?
Известно, что 1 литр кваса в Цветочном городе
стоит 1 монету, 1 литр газировки – 3 монеты, 1 литр
малинового сиропа – 6 монет, 1 литр касторки – 2
монеты.
- Сколько монет истратил на покупку напитков
каждый человечек? - Сколько монет затрачено на покупку напитков
каждого вида? - Сколько потрачено денег всеми человечками
вместе?
Литература
- Информатика. Задачник-практикум в 2 т. /Под ред.
И.Г.Семакина, Е.К.Хеннера – М.: Лаборатория
Базовых Знаний, 2010. - Ефимова О. Курс компьютерной технологии с
основами информатики. – М.: ООО “издательство
АСТ”; АВF, 2005.
Презентация
В программе Excel разработчиками заложено огромное количество различных функций, но, пользователи чаще всего пользуются математическими. Давайте рассмотрим их и подробнее остановимся на самых популярных.
-
Использование математических функций в программе
- СУММ
- СУММЕСЛИ
- ПРОИЗВЕД
- ЧАСТНОЕ
- СТЕПЕНЬ
-
КОРЕНЬ
- ОКРУГЛ
- ABS
- LOG
- ОСТАТОК
- Заключение
Использование математических функций в программе
В категорию математических функций входит более 60 различных операторов, которые позволяют выполнять различные вычисления.
Вставить функцию в свободную ячейку таблицы можно по-разному:
- Жмем кнопку “Вставить функцию” (fx) слева от строки формул. Выполнить данное действие можно, находясь в любой вкладке.
- Переключаемся во вкладку “Формулы”. Здесь также представлена кнопка “Вставить функцию” – в левом углу ленты инструментов.
- Нажимаем комбинацию клавиш Shift+F3, чтобы вызвать Мастер функций.
Результатом любого из вышеописанных способов будет открытие окна вставки функции. Здесь мы выбираем категорию “Математические”.
Теперь, когда категория выбрана, в поле ниже отмечаем требуемую функцию и щелкаем OK.
После этого откроется окно с аргументами для заполнения.
Примечание: Если мы, находясь во вкладке “Формулы”, в группе инструментов “Библиотека функций” нажмем по значку математических функций, сразу откроется список операторов, которые мы можем выбрать, минуя окно вставки функции.
Стоит учитывать, что в предлагаемом перечне присутствуют не все операторы, но самые необходимые здесь все же есть, и в большинстве случаев их достаточно.
Теперь перейдем к детальному рассмотрению самых популярных функций.
СУММ
Пожалуй, это самая популярная функция, которая используется в Эксель. С помощью нее выполняется суммирование числовых данных. Формула функции:
=СУММ(число1;число2;...)
В аргументах можно указать как конкретные числа, так и ссылки на ячейки, содержащие числовые значения. Причем указать координаты можно вручную (с помощью клавиш клавиатуры) или методом клика/выделения непосредственно в самой таблице.
Для перехода к заполнению следующего аргумента достаточно кликнуть по полю напротив него или нажать клавишу Tab.
СУММЕСЛИ
Данная функция позволяет считать сумму чисел с заданным условиями, с помощью которых будет выполняться отбор значений, учитывающихся в суммировании. Формула выглядит следующим образом:
=СУММЕСЛИ(Диапазон;Критерий;Диапазон_суммирования)
В аргументах функции указывается диапазон ячеек (вручную или путем выделения в таблице), значения которых нужно просуммировать. В качестве критерия можно задать следующие условия (в кавычках):
- больше (“>”)
- меньше (“<“)
- не равно (“<>”)
Аргумент “Диапазон_сумирования” заполнять не обязательно.
ПРОИЗВЕД
С помощью данного оператора выполняется умножение чисел. Синтаксис выглядит следующим образом:
=ПРОИЗВЕД(число;число;…)
В аргументах функции, как и в СУММ, можно указывать как конкретные числа, так и адреса ячеек (диапазоны ячеек), которые содержат числовые значения.
ЧАСТНОЕ
Чаще всего для деления используется формула со знаком “/” между делимым и делителем: =Число1/Число2.
Однако в программе также есть отдельная функция для выполнения деления, синтаксис которой представлен ниже:
=ЧАСТНОЕ(Числитель;Знаменатель)
Заполнить нужно два аргумента: Числитель (Делимое) и Знаменатель (Делитель).
СТЕПЕНЬ
Оператор позволяет возвести число в указанную степень. Формула выглядит так:
=СТЕПЕНЬ(число;степень)
В аргументах функции указывается само число, а также, степень, в которую нужно его возвести.
КОРЕНЬ
С помощью данного оператора можно извлечь квадратный корень из числа. Синтаксис выглядит следующим образом:
=КОРЕНЬ(число)
Заполнить требуется только один аргумент – “Число”.
ОКРУГЛ
Функция применяется для выполнения еще одного распространенного математического действия – округления чисел (по общематематическим правилам, т.е., к ближайшему по модулю значению). Синтаксис функции представлен ниже:
=ОКРУГЛ(число;число_разрядов)
В аргументе “Число” указывается значение, которое требуется округлить. В числе разрядов, соответственно, пишем количество цифр, которые хотим оставить после запятой.
Также, в Excel доступны операторы ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ, которые, как следует из их названий, используются для округления до ближайшего верхнего и нижнего числа, соответственно (по модулю).
ABS
Позволяет получить модуль числа. Формула функции представлена ниже:
=ABS(число)
Заполнить нужно всего один аргумент – “Число”, модуль которого требуется найти.
LOG
С помощью этого оператора определяется логарифм числа по заданному основанию. Синтаксис функции представлен в виде:
=LOG(Число;Основание)
Необходимо заполнить два аргумента: Число и Основание логарифма (если его не указать, программа примет значение по умолчанию, равное 10).
Также для десятичного логарифма предусмотрена отдельная функция – LOG10.
ОСТАТОК
Применяется для получения остатка от деления чисел. Формула оператора выглядит следующим образом:
=ОСТАТ(чило;делитель)
Для того, чтобы получить результат, требуется заполнить значения двух аргументов: Число и Делитель.
Заключение
Таким образом, мы разобрали самые популярные математические функции, которые используются в Excel. Однако возможности программы гораздо шире, и в ее инструментарии можно найти функцию для успешного выполнения практически любой задачи.
Решение математической задачи
с использованием компьютерного моделирования.
Этап
1. Постановка задачи.
Под задачей понимается некая проблема, которую надо решить. На
этапе постановки задачи необходимо:
1. описать
задачу,
2. определить
цели моделирования,
3. проанализировать
объект или процесс.
Описание задачи. Задача формулируется
на обычном языке, и описание должно быть понятным. Главное здесь — определить
объект моделирования и понять, что должен представлять собой результат.
Даны координаты двух противоположных вершин прямоугольника:
A(x1, y1), C(x2, y2). Стороны прямоугольника параллельны осям координат. Определить
в какой четверти координатной плоскости находится прямоугольник. Предложите
свои координаты, чтобы прямоугольник находился во 2 и 3 четвертях координатной
плоскости. Найдите периметр и площадь прямоугольника.
Цели
моделирования.
1. Познание
окружающего мира.
Зачем
человек создает модели? Чтобы ответить на этот вопрос, надо заглянуть в далекое
прошлое. Несколько миллионов лет назад, на заре человечества, первобытные люди
изучали окружающую природу, чтобы научиться противостоять природным стихиям,
пользоваться природными благами, просто выживать. Накопленные знания
передавались из поколения в поколение устно, позже письменно, наконец с помощью
предметных моделей. Так родилась, к примеру, модель земного шара — глобус, —
позволяющая получить наглядное представление о форме нашей планеты, ее вращении
вокруг собственной оси и расположении материков. Такие модели позволяют понять,
как устроен конкретный объект, узнать его основные свойства, установить законы
его развития и взаимодействия с окружающим миром моделей.
- Создание объектов с заданными свойствами (задача
типа «Как сделать, чтобы…»).
Накопив
достаточно знаний, человек задал себе вопрос: «Нельзя ли создать объект с
заданными свойствами и возможностями, чтобы противодействовать стихиям или
ставить себе на службу природные явления?» Человек стал строить модели еще не
существующих объектов. Так родились идеи создания ветряных мельниц, различных
механизмов, даже обыкновенного зонтика. Многие из этих моделей стали в
настоящее время реальностью. Это объекты, созданные руками человека.
- Определение последствий воздействия на объект и
принятие правильного решения (задача типа «Что будет,
если…»: что будет, если увеличить плату за проезд в транспорте, или что
произойдет, если закопать ядерные отходы в такой-то местности?)
Например,
для спасения Петербурга от постоянных наводнений, приносящих огромный ущерб,
решено было возвести дамбу. При ее проектировании было построено множество
моделей, в том числе и натурных, именно для того, чтобы предсказать последствия
вмешательства в природу.
- Эффективность управления объектом (или
процессом).
Поскольку
критерии управления бывают весьма противоречивыми, то эффективным оно окажется
только при условии, если будут «и волки сыты, и овцы целы». Например, нужно
наладить питание в школьной столовой. С одной стороны, оно должно отвечать
возрастным требованиям (калорийное, содержащее витамины и минеральные соли), с
другой — нравиться большинству ребят и к тому же быть «по карману» родителям, а
с третьей — технология приготовления должна соответствовать возможностям
школьных столовых. Как совместить несовместимое? Построение модели поможет
найти приемлемое решение.
Определить координаты вершин B и D. Вычислить площадь и периметр
прямоугольника.
Выявить взаимосвязь между координатами вершин и расположением
прямоугольника на координатной плоскости.
Анализ
объекта.
На
этом этапе четко выделяют моделируемый объект, его основные свойства, его
элементы и связи между ними. Простой пример подчиненных связей объектов —
разбор предложения. Сначала выделяются главные члены (подлежащее, сказуемое),
затем второстепенные члены, относящиеся к главным, затем слова, относящиеся к
второстепенным, и т. д.
|
Что моделируется? |
Система, состоящая из двух простых объектов: прямоугольника и |
|
Что известно о прямоугольнике? |
Прямоугольник задан двумя про-тивоположными вершинами А и С. |
|
Чем характеризуется система координат? Система координат — это две взаимно перпендикулярные Оси координат делят плоскость на 4 угла, которые называют координатными |
|
Этап
2. Разработка модели.
Информационная модель.
На этом этапе выясняются свойства,
состояния, действия и другие характеристики элементарных объектов в любой
форме: устно, в виде схем, таблиц. Формируется представление об элементарных
объектах, составляющих исходный объект, т. е. информационная модель. Модели
должны отражать наиболее существенные признаки, свойства, состояния и отношения
объектов предметного мира. Именно они дают полную информацию об объекте.
Например, в школе учащиеся знакомятся с
информационной моделью кровообращения. Предлагаемой в учебнике анатомии
информации достаточно для школьника, но мало для тех, кто проводит операции на
сосудах в больницах.
Информационные модели играют очень
важную роль в жизни человека.
Знания, получаемые вами в школе, имеют
вид информационной модели, цель которой — изучение предметов и явлений.
Уроки истории дают возможность построить
модель развития общества, а знание этой модели позволяет строить собственную
жизнь, либо повторяя ошибки предков, либо учитывая их.
На уроках географии вам сообщают
информацию о географических объектах: горах, реках, странах и др. Это тоже
информационные модели. Многое, о чем рассказывается на занятиях по географии,
вы никогда не увидите в реальности.
На уроках химии информация о свойствах
разных веществ и законах их взаимодействия подкрепляется опытами, которые есть
не что иное, как реальные модели химических процессов.
Информационная модель никогда не
характеризует объект полностью. Для одного и того же объекта можно построить
различные информационные модели.
Выбор наиболее существенной информации
при создании информационной модели и сложность этой модели обусловлены целью
моделирования.
Построение информационной модели
является отправным пунктом этапа разработки модели. Все входные параметры
объектов, выделенные при анализе, располагают в порядке убывания значимости и
проводят упрощение модели в соответствии с целью моделирования.
Знаковая модель.

чем приступить к процессу моделирования, человек делает предварительные
наброски чертежей либо схем на бумаге, выводит расчетные формулы, т. е.
составляет информационную модель в той или иной знаковой форме, которая может
быть либо компьютерной, либо некомпьютерной.
Рисуем прямоугольник, отмечаем что дано, определяем, как найти
координаты двух других вершин.
Компьютерная модель
— это модель, реализованная средствами
программной среды.
Существует множество программных
комплексов, которые позволяют проводить исследование (моделирование)
информационных моделей. Каждая программная среда имеет свой инструментарий и
позволяет работать с определенными видами информационных объектов.
Человек уже знает, какова будет модель,
и использует компьютер для придания ей знаковой формы. Например, для построения
геометрических моделей, схем используются графические среды, для словесных или
табличных описаний — среда текстового редактора.
Основные функции компьютера при
моделировании систем:
·
исполнение роли вспомогательного средства для решения задач,
решаемых и обычными вычислительными средствами, алгоритмами, технологиями;
·

постановки и решения новых задач, не решаемых традиционными средствами,
алгоритмами, технологиями;
·
исполнение роли средства конструирования компьютерных обучающих
и моделирующих сред типа: «обучаемый — компьютер — обучающий», «обучающий —
компьютер — обучаемый», «обучающий — компьютер — группа обучаемых», «группа
обучаемых — компьютер — обучающий», «компьютер — обучаемый — компьютер»;
·
исполнение роли средства моделирования для получения новых
знаний;
·
«обучение» новых моделей (самообучение моделей).
Выбираем для создания модели нашей задачи Microsoft Office Excel.
Строим таблицу для ввода заданных координат, для вычисления не заданных
координат, площади и периметра вводим формулы, строим по таблице график.
Этап
3. Компьютерный эксперимент.
Компьютерное моделирование — основа
представления знаний в ЭВМ. Компьютерное моделирование для рождения новой
информации использует любую информацию, которую можно актуализировать с помощью
ЭВМ. Прогресс моделирования связан с разработкой систем компьютерного
моделирования, а прогресс в информационной технологии — с актуализацией опыта
моделирования на компьютере, с созданием банков моделей, методов и программных
систем, позволяющих собирать новые модели из моделей банка.
Разновидность компьютерного
моделирования — вычислительный эксперимент, т. е. эксперимент, осуществляемый
экспериментатором над исследуемой системой или процессом с помощью орудия
эксперимента — компьютера, компьютерной среды, технологии.
Вычислительный эксперимент становится
новым инструментом, методом научного познания, новой технологией также из-за
возрастающей необходимости перехода от исследования линейных математических
моделей систем (для которых достаточно хорошо известны или разработаны методы
исследования, теория) к исследованию сложных и нелинейных математических
моделей систем (анализ которых гораздо сложнее). Грубо говоря, наши знания об
окружающем мире линейны, а процессы в окружающем мире нелинейны.
Вычислительный эксперимент позволяет
находить новые закономерности, проверять гипотезы, визуализировать ход событий
и т. д.
Чтобы дать жизнь новым конструкторским
разработкам, внедрить новые технические решения в производство или проверить
новые идеи, нужен эксперимент. В недалеком прошлом такой эксперимент можно было
провести либо в лабораторных условиях на специально создаваемых для него
установках, либо на натуре, т. е. на настоящем образце изделия, подвергая его
всяческим испытаниям.
С развитием вычислительной техники
появился новый уникальный метод исследования — компьютерный эксперимент.
Компьютерный эксперимент включает некоторую последовательность работы с
моделью, совокупность целенаправленных действий пользователя над компьютерной
моделью.
В нашей задаче меняем координаты вершин А и С, смотрим за
изменениями на графике и проверяем расчеты по формулам.
Эксперимент 1 Вводимые
координаты положительные
Эксперимент 2 Вводимые
координаты отрицательные
Эксперимент 3 Вводимые
координаты (x) отрицательные, (y)
положительные
Эксперимент 4 Вводимые
координаты (у) отрицательные, (х) положительные
Эксперимент 5 Вводимая
координата (у) вершины С отрицательна, все остальные положительные
Эксперимент 6 Вводимая
координата (у) вершины С положительна, все остальные отрицательные
Эксперимент 7 Вводимые
координаты одной заданной вершины положительные, другой вершины отрицательные
Этап
4. Анализ результатов моделирования.
Конечная цель моделирования — принятие решения,
которое должно быть выработано на основе всестороннего анализа полученных
результатов. Этот этап решающий — либо вы продолжаете исследование, либо
заканчиваете. Возможно, вам известен ожидаемый результат, тогда необходимо
сравнить полученный и ожидаемый результаты. В случае совпадения вы сможете
принять решение.
Основой для выработки решения служат
результаты тестирования и экспериментов. Если результаты не соответствуют целям
поставленной задачи, значит, допущены ошибки на предыдущих этапах. Это может
быть либо слишком упрощенное построение информационной модели, либо неудачный
выбор метода или среды моделирования, либо нарушение технологических приемов
при построении модели. Если такие ошибки выявлены, то
требуется корректировка модели, т. е. возврат к одному из предыдущих
этапов. Процесс повторяется до тех пор, пока результаты эксперимента
не будут отвечать целям моделирования. Главное, надо всегда помнить:
выявленная ошибка — тоже результат.
Как говорит народная мудрость, на ошибках учатся.
Теперь учащиеся смогут построить прямоугольник в любой четверти
координатной плоскости.
Для квадрата со стороной a периметр P можно
вычислить с помощью следующих формул
Переходим к
формулам для двух огородов в форме прямоугольников. Обозначим через b меньшую сторону прямоугольника, а через q отношение его сторон (для первого прямоугольника q=2, для второго – q=3).
Тогда формулы для вычисления периметра в случае прямоугольника можно записать
так
Рассмотрим теперь формулы для выбора самого короткого забора вокруг
четырех огородов. Пусть i – порядковый номер огорода, Pi – периметр i – го
огорода, Pmin – искомый минимальный
периметр. Тогда можно написать формулу
Обозначим буквой T – форму огорода с
самым коротким забором и напишем формулу для ее автоматического вычисления
Легко проверить, что условия задачи позволяют выполнить расчеты по
формулам (3.1)-(3.5) и найти решение поставленной задачи.
3.4. Описание решения задачи
Фрагмент рабочего листа Excel с решением
задачи об огородах (см. рис. 3.1) дает пример возможного оформления результатов
вычислений.
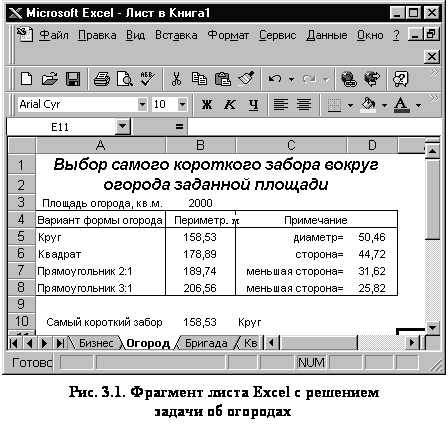 |
Ввод и форматирование заголовка произведено так, как описано в
задачах о платежной ведомости и об оптимальном бизнесе. Заданная площадь
огородов введена в ячейку B3. Расчеты, связанные с
определением длины заборов вокруг огородов, представлены в табличной форме в
ячейках интервала A4:D8. Первая
колонка таблицы представляет варианты формы огородов. Длина заборов (периметры),
вычисленная по формулам (3.1)-(3.3), видна во втором столбце таблицы.
Вспомогательные величины вычислены в ячейках интервала D5:D8 и вместе с кратким пояснением в ячейках C5:C8 образуют третий столбец таблицы (см. рис. 3.1). Например,
для квадрата в ячейку D6 введена формула =КОРЕНЬ(B3), обеспечивающая вычисление стороны, а в ячейку B6 формула =4*D6 для вычисления
периметра. Копирование этих формул в другие ячейки не производилось, поэтому в
них можно использовать ссылки на ячейки любого типа. Основу указанных двух
формул составляют формулы (3.2) из подраздела 3.3.
Наибольший интерес представляют формулы в ячейках B10
и C10. В ячейку B10 введена
формула =МИН($B$5:$B$8),
реализующая вычисление минимального периметра Pmin
по формуле (3.4). Более сложна формула в ячейке C10
=ЕСЛИ(B5=B10;A5;ЕСЛИ(B6=B10;A6;ЕСЛИ(B7=B10;A7;A8)))
Она реализует выбор варианта формы огорода с минимальным периметром
в точном соответствии с формулой (3.5). Пояснения по использованию логической
функции ЕСЛИ имеются в подразделе 2.4.
3.5. Выводы
Результаты решения задачи соответствуют известному математическому
факту: чем более «правильную» форму имеет плоская фигура заданной площади, тем
меньше ее периметр. Периметры огородов в форме круга, квадрата и двух прямоугольников
(см. рис. 3.1) увеличиваются по мере уклонения их формы от «правильной».
Наименьший периметр 158,53 м имеет огород в форме круга. Наибольший периметр
206,56 м у прямоугольника с отношением сторон 3:1. Следовательно, по
сравнению с круглым огородом забор для второго прямоугольного огорода на
48,03 м длиннее. Соответственно увеличиваются затраты на его
строительство.
На практике круглые огороды не очень распространены. Поэтому из
трех других вариантов формы следует выбрать квадрат, у которого периметр
меньше, чем у остальных.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание – внизу страницы.

























