–
Здравствуйте, ребята. Посмотрите, какая отличная фотография моего брата Умножение.
Но
я решил рамочку украсить. У меня есть симпатичные бусы, которые висели на
новогодней ёлке. Но сейчас я хочу их использовать для украшения рамки. Только
надо сначала точно отмерить кусок нужной длины.
Рамка
имеет форму прямоугольника. Бусы я приклею по периметру рамки. Сначала я
линейкой измерю стороны рамки:
Теперь
можно найти периметр прямоугольника, то есть сумму длин всех его сторон:
Да,
не очень удобный способ вычисления. А если когда-нибудь придётся находить
периметр большого предмета – например, комнаты или дома. Надо-ка мне подумать,
может быть, есть более удобный способ нахождения периметра прямоугольника?
А
вот если так: переставлю-ка я числа. Ведь я помню переместительный закон
сложения – от перестановки слагаемых сумма не меняется.
Так,
пожалуй, тоже не очень удобно, но кажется, я понял! Посмотрите! В этой записи
рядом стоят две пары одинаковых чисел. А ведь сумму одинаковых слагаемых можно
заменить умножением. И я сейчас эту запись немножко переделаю. Вместо
суммы чисел я запишу:
Да,
если хорошо знаешь таблицу умножения на 2:
Такой
способ вычисления более удобен. Находим две длины, то есть длину умножаем на
два, потом находим две ширины – ширину умножаем на два. А после этого
складываем между собой результаты. Неплохое получилось решение, но если бы я не
переставлял множители, и запись оставалась прежней, то здесь можно было бы
использовать сочетательное свойство сложения и вычислять так:
Заменим
умножением и получим:
А
вот эта запись мне нравится ещё больше. Посмотрите – здесь уже не три, а два
действия. Сначала находим сумму длины и ширины а, так как в прямоугольнике две
такие пары, то эту сумму умножаем на два.
Этот
способ можно назвать рациональным, то есть, наиболее удобным и коротким,
потому что в нём меньше действий, чем в предыдущих способах.
Да,
кажется, я здорово потрудился – вывел аж три способа нахождения периметра
прямоугольника:
·
простое
сложение всех четырёх сторон прямоугольника.
·
сначала
находим две длины, потом две ширины, а потом результаты складываем.
·
находим
сумму длины и ширины и результат умножаем на два.
Конечно,
любой способ решения будет верным. Главное, не допустить ошибки в вычислениях.
Но ведь вы уже не первоклашки! Вы умеете умножать на два! Поэтому я думаю, что
вы воспользуетесь вторым способом, или третьим. Выберете тот способ, который
будет удобнее и легче при решении задачи.
Ну,
а я уже знаю, какой длины мне нужны бусы, чтобы украсить рамочку с фотографией знака
Умножение. Пойду украшать рамочку. До свидания, ребята!
Содержание:
- § 1 Что такое периметр
- § 2 Прямоугольник и его периметр
§ 1 Что такое периметр
В этом уроке научимся вычислять периметр многоугольника.
Рассмотрим задачу.

Чтобы узнать длину всего забора, необходимо измерить стороны вольера. Вольер имеет форму четырехугольника. У четырехугольника 4 стороны. Измерим стороны четырехугольника: одна сторона 6 м, вторая сторона 4 м, третья – 5 м, четвертая – 5 м.
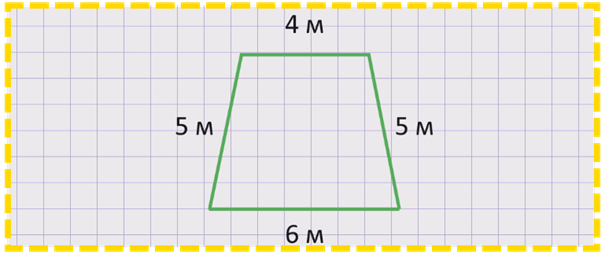
Найдем сумму длин сторон четырехугольника. Для этого нужно сложить длины всех его сторон:

Так как сумма длин всех сторон четырехугольника, составляющих забор вольера, равна 20 метров, значит, 20 метров забора требуется заменить.

§ 2 Прямоугольник и его периметр


У прямоугольника 4 стороны, но так как противоположные стороны его равны, то для вычисления достаточно знать длины двух разных сторон. Большая сторона прямоугольника называется длиной, меньшая сторона – шириной.

Измерим длину и ширину нашего прямоугольника: длина 5 см, ширина 3 см. Найдем периметр прямоугольника: 5 см + 5 см + 3 см + 3 см = 16 см.

Периметр прямоугольника составляет 16 см.
Периметр можно найти у любой геометрической фигуры.

Решим задачу:
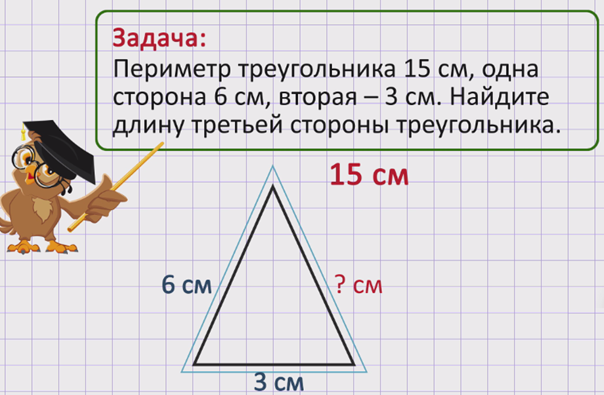
Периметр – это сумма длин всех сторон многоугольника. Значит, периметр – это целое. Нужно найти длину стороны треугольника, то есть часть периметра. Чтобы найти неизвестную часть, нужно из целого вычесть известные части, то есть из значения периметра вычесть значения длин первой и второй сторон:

Длина третьей стороны треугольника 6 см.
Список использованной литературы:
- Петерсон Л.Г. Математика 1 класс: Методические рекомендации. Пособие для учителя. – М.: Ювента.
- Петерсон Л.Г. Математика. 1 класс: Ч. 1-3 – М.: Баласс, 2009.
Использованные изображения:
Видеоурок как найти периметр прямоугольника

Как найти периметр прямоугольника и квадрата

Математика 2 класс (Урок№49 – Периметр прямоугольника.)

Как объяснить ребенку тему “Периметр” | Что такое “периметр”
Урок 21. Периметр прямоугольника
ВИДЕОУРОК
Периметр прямоугольника.
На практике очень
часто приходится решать задачи по определению периметра прямоугольника.
Прямоугольник – это фигура, лежащая в одной плоскости. Если
мы измерим и сложим все стороны прямоугольника, то получим число, которое
называется периметром данного прямоугольника. Если в прямоугольнике обозначим
одну из сторон а, а вторую b, то периметр прямоугольника Р будет
равен:

Найти периметр прямоугольника – это значит
вычислить сумму его сторон. Если периметр – это сумма длин всех сторон фигуры,
то полупериметр – сумма одной длины и одной ширины.
![]()
ЗАДАЧА:
Периметр
прямоугольника 26 см, а одна сторона его равна 5 см. Найдите другую
сторону.
РЕШЕНИЕ:
Здесь Р = 26 см,
допустим, что а = 5 см.
Подставив значения Р и а в формулу,
![]()
получим уравнение
26 = 2(5 + b).
Решим его:
2(5 + b) = 26,
5 + b = 26 : 2,
5 + b = 13,
b = 13 – 5, b = 8.
ЗАДАЧА:
Биссектриса угла С прямоугольника АВСD пересекает сторону АD в точке
К,
DК = 4
см, АК
= 6
см.
Найдите периметр прямоугольника.
РЕШЕНИЕ:
∠ КСD = 90° : 2 = 45°,
З ∆ СDК:
СD = КD = 4 (см).
Р = 2(4 + (6 + 4)) = 28 (см).
ЗАДАЧА:
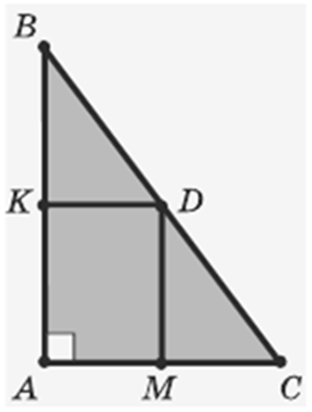
В прямоугольном
треугольнике через середину его гипотенузы проведены прямые, параллельные
катетам. Найдите периметр образовавшегося прямоугольника, если катеты
треугольника равны 10 см и 8 см.
РЕШЕНИЕ:
Начертим
чертёж.
Из условия задачи имеем:
∆ АВС – прямоугольный,
∠ А – прямой,
D – середина гипотенузы.
КD ∥ АС, DМ ∥ АВ.
Катеты равны 10 см и 8 см.
Так как
КD = 1/2 АС = 4 см,
МD = 1/2 АВ = 5 см,
согласно свойству
средней линии треугольника, то периметр прямоугольника АКDМ равен:
Р = 2(4 + 5) = 18 (см).
ЗАДАЧА:
Биссектриса одного из углов прямоугольника делит сторону
прямоугольника пополам. Найдите периметр прямоугольника, если его меньшая
сторона равна 10 см.
РЕШЕНИЕ:

∠ 1 = ∠ 2 (так как АО – биссектриса).
∠ 2 = ∠ 3 (как накрест
лежащие углы для прямых ВС, АD и
секущей АО).
Значит, ∠ 1 = ∠ 3 и ∆ АОВ – равнобедренный.
Поэтому
АВ = ВО = 10 см (стороны
равнобедренного треугольника).
ВО = ОС (по условию). Значит, ОС = 10 см,
ВС = ВО + ОС =
10 см + 10 см = 20 см.
РАВСВ = 2(АВ + ВС) =
2(10 см + 20 см) = 60 см.
ОТВЕТ: 60 см
ЗАДАЧА:
В прямоугольнику биссектриса одного из углов делит
сторону на отрезки 20 см и 30
см. Найдите периметр прямоугольника.
РЕШЕНИЕ:
Так как сторона прямоугольника делится на отрезки 20
см и
30
см, то её длина – 50
см. Противоположная ей сторона также равна
50
см.
Другая сторона прямоугольника может быть как 20
см так и
30 см.
Поэтому:
а) Если другая сторона 20
см и противоположная ей сторона 20
см, то периметр прямоугольника
20 см + 20 см + 50 см + 50 см = 140 см.
б) Если другая сторона 30
см и противоположная ей сторона 30
см, то периметр прямоугольника
30 см + 30 см + 50 см + 50 см = 160 см.
ОТВЕТ:
140 см або 160 см
Задания к уроку 21
- Задание 1
- Задание 2
- Задание 3
Другие уроки:
- Урок 1. Точка и прямая
- Урок 2. Угол
- Урок 3. Параллельные и перпендикулярные прямые
- Урок 4. Окружность
- Урок 5. Угол и окружность
- Урок 6. Треугольник (1)
- Урок 7. Треугольник (2)
- Урок 8. Прямоугольный треугольник (1)
- Урок 9. Прямоугольный треугольник (2)
- Урок 10. Равнобедренный треугольник (1)
- Урок 11. Равнобедренный треугольник (2)
- Урок 12. Периметр треугольника
- Урок 13. Периметр равнобедренного (равностороннего) треугольника
- Урок 14. Треугольник и окружность
- Урок 15. Прямоугольный треугольник и окружность
- Урок 16. Равнобедренный треугольник и окружность
- Урок 17. Четырёхугольники
- Урок 18. Параллелограмм
- Урок 19. Периметр параллелограмма
- Урок 20. Прямоугольник
- Урок 22. Квадрат
- Урок 23. Ромб
- Урок 24. Периметр ромба
- Урок 25. Трапеция
- Урок 26. Равнобедренная трапеция
- Урок 27. Периметр трапеции
- Урок 28. Четырёхугольник и окружность (1)
- Урок 29. Четырёхугольник и окружность (2)
- Урок 30. Многоугольник
- Урок 31. Правильный многоугольник
- Урок 32. Осевая и центральная симметрии
Нам кажется, что на видео есть . Посмотреть
Уберите лишние метки и подтвердите оставшиеся, если они определены верно
Убраны из меток0
Подтвердить метки
Отмена
Периметр прямоугольника. 2 класс
На видео отмечены:
14 апр 2020559 просмотров
-
Комментарии0
-
6
-
Добавить в закладки
-
-
Пожаловаться
-