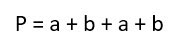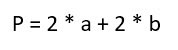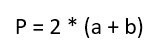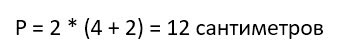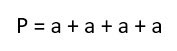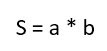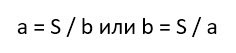Видеоурок периметр и площадь прямоугольника
Периметр и площадь квадрата и прямоугольника.
Математика 3 класс (Урок№22 – Площадь прямоугольника.)
Площадь прямоугольника | Математика 3 класс #16 | Инфоурок
–
Здравствуйте, ребята. Посмотрите, какая отличная фотография моего брата Умножение.
Но
я решил рамочку украсить. У меня есть симпатичные бусы, которые висели на
новогодней ёлке. Но сейчас я хочу их использовать для украшения рамки. Только
надо сначала точно отмерить кусок нужной длины.
Рамка
имеет форму прямоугольника. Бусы я приклею по периметру рамки. Сначала я
линейкой измерю стороны рамки:
Теперь
можно найти периметр прямоугольника, то есть сумму длин всех его сторон:
Да,
не очень удобный способ вычисления. А если когда-нибудь придётся находить
периметр большого предмета – например, комнаты или дома. Надо-ка мне подумать,
может быть, есть более удобный способ нахождения периметра прямоугольника?
А
вот если так: переставлю-ка я числа. Ведь я помню переместительный закон
сложения – от перестановки слагаемых сумма не меняется.
Так,
пожалуй, тоже не очень удобно, но кажется, я понял! Посмотрите! В этой записи
рядом стоят две пары одинаковых чисел. А ведь сумму одинаковых слагаемых можно
заменить умножением. И я сейчас эту запись немножко переделаю. Вместо
суммы чисел я запишу:
Да,
если хорошо знаешь таблицу умножения на 2:
Такой
способ вычисления более удобен. Находим две длины, то есть длину умножаем на
два, потом находим две ширины – ширину умножаем на два. А после этого
складываем между собой результаты. Неплохое получилось решение, но если бы я не
переставлял множители, и запись оставалась прежней, то здесь можно было бы
использовать сочетательное свойство сложения и вычислять так:
Заменим
умножением и получим:
А
вот эта запись мне нравится ещё больше. Посмотрите – здесь уже не три, а два
действия. Сначала находим сумму длины и ширины а, так как в прямоугольнике две
такие пары, то эту сумму умножаем на два.
Этот
способ можно назвать рациональным, то есть, наиболее удобным и коротким,
потому что в нём меньше действий, чем в предыдущих способах.
Да,
кажется, я здорово потрудился – вывел аж три способа нахождения периметра
прямоугольника:
·
простое
сложение всех четырёх сторон прямоугольника.
·
сначала
находим две длины, потом две ширины, а потом результаты складываем.
·
находим
сумму длины и ширины и результат умножаем на два.
Конечно,
любой способ решения будет верным. Главное, не допустить ошибки в вычислениях.
Но ведь вы уже не первоклашки! Вы умеете умножать на два! Поэтому я думаю, что
вы воспользуетесь вторым способом, или третьим. Выберете тот способ, который
будет удобнее и легче при решении задачи.
Ну,
а я уже знаю, какой длины мне нужны бусы, чтобы украсить рамочку с фотографией знака
Умножение. Пойду украшать рамочку. До свидания, ребята!
Содержание:
- § 1 Что такое периметр
- § 2 Прямоугольник и его периметр
§ 1 Что такое периметр
В этом уроке научимся вычислять периметр многоугольника.
Рассмотрим задачу.
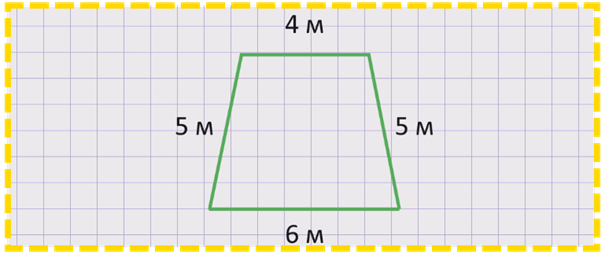
Чтобы узнать длину всего забора, необходимо измерить стороны вольера. Вольер имеет форму четырехугольника. У четырехугольника 4 стороны. Измерим стороны четырехугольника: одна сторона 6 м, вторая сторона 4 м, третья – 5 м, четвертая – 5 м.
Найдем сумму длин сторон четырехугольника. Для этого нужно сложить длины всех его сторон:
Так как сумма длин всех сторон четырехугольника, составляющих забор вольера, равна 20 метров, значит, 20 метров забора требуется заменить.
§ 2 Прямоугольник и его периметр

У прямоугольника 4 стороны, но так как противоположные стороны его равны, то для вычисления достаточно знать длины двух разных сторон. Большая сторона прямоугольника называется длиной, меньшая сторона – шириной.
Измерим длину и ширину нашего прямоугольника: длина 5 см, ширина 3 см. Найдем периметр прямоугольника: 5 см + 5 см + 3 см + 3 см = 16 см.
Периметр прямоугольника составляет 16 см.
Периметр можно найти у любой геометрической фигуры.
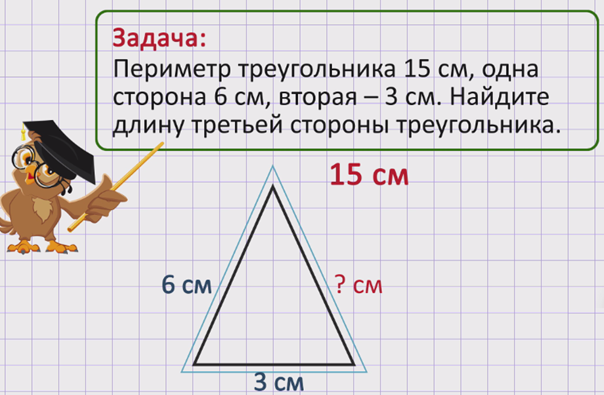
Решим задачу:
Периметр – это сумма длин всех сторон многоугольника. Значит, периметр – это целое. Нужно найти длину стороны треугольника, то есть часть периметра. Чтобы найти неизвестную часть, нужно из целого вычесть известные части, то есть из значения периметра вычесть значения длин первой и второй сторон:
Длина третьей стороны треугольника 6 см.
Список использованной литературы:
- Петерсон Л.Г. Математика 1 класс: Методические рекомендации. Пособие для учителя. – М.: Ювента.
- Петерсон Л.Г. Математика. 1 класс: Ч. 1-3 – М.: Баласс, 2009.
Использованные изображения:
|
Правила поведения учеников [6] |
|
Советы по воспитанию [6] |
|
Советы психолога [100] |
|
Советы логопеда [28] |
|
Что должен знать и уметь ученик? [2] |
|
Рекомендации по обучению [1] |
|
Памятка школьнику [13] |
|
Заповеди родителей [7] |
|
Памятка учителю [21] |
|
Критерии оценивания по предметам [4] |
|
Будущим первоклассникам [58] |
|
ФГОС [1] |
|
Русский язык 3 класс [11] |
|
Математика 3 класс [12] |
|
Окружающий мир [9] |
|
Фильмы и мультфильмы [45] |
|
Технология (творчество) [11] |
|
ИЗО [7] |
|
Физминутки [12] |
|
Основы безопасности [25] |
|
Контрольные работы (тренироваться) [1] |
|
Библиотека [1] |
|
Чтение [17] |
|
Здоровье [18] |
|
Праздники и обычаи [18] |
|
Интересные факты [14] |
|
Дискотека [1] |
|
Развлечения [7] |
|
Радио [1] |
|
Музыка [0] |
|
Релакс [1] |
|
Игровая комната для девочек [0] |
|
Игровая комната для мальчиков [0] |
|
Игры онлайн [3] |
|
Юмор [2] |
|
Информатика [3] |
|
Английский язык [11] |
|
Энциклопедии и словари [2] |
|
Флэш- игры по английскому языку [13] |
|
Развитие речи [1] |
|
Флэш- игры по окружающему миру [10] |
|
Олимпиада по литературному чтению [11] |
|
Флэш- игры по математике [26] |
|
Олимпиада по русскому языку [12] |
|
Флэш- игры по русскому языку [3] |
|
Олимпиада по математике [5] |
|
Стихи [16] |
|
ОРКСЭ [2] |
|
Контрольные по математике [0] |
|
Тесты по математике [0] |
|
Диктанты по русскому языку [6] |
|
Памятки с правилами по русскому языку [27] |
|
Тесты по русскому языку [23] |
|
Биография некоторых авторов [7] |
|
Читаем онлайн [3] |
|
Сказки, рассказы, притчи [3] |
|
Сайты по русскому языку с правилами и тестами [3] |
|
Видеоуроки на все правила по русскому языку [19] |
|
Видеоуроки на все правила по математике [35] |
|
Тесты онлайн по математике [16] |
|
Контрольные работы по математике [11] |
|
Памятки по математике [4] |
|
Арифметические диктанты [5] |
|
Развлекалки для детей [1] |
|
Игры для страницы “Переменка” [8] |
|
Видеоуроки на все темы по окружающему миру [46] |
|
Ответы почемучкам [12] |
|
Тесты онлайн по окружающему миру [5] |
|
Пасха [3] |
|
Масленица [2] |
|
Рождество [2] |
|
Вкусняшки [1] |
|
Коктейли [28] |
|
Конфеты [1] |
Периметр прямоугольника
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы расскажем, что такое периметр прямоугольника и по каким формулам его можно посчитать.
Тема в общем-то простая, каждый из нас изучал ее еще в начальных классах. Тем не менее с возрастом кто-то мог что-нибудь и подзабыть.
Но для начала предлагаем освежить теоретическую базу и вспомнить, что такое прямоугольник.
Что такое прямоугольник и что такое периметр
Прямоугольник – это геометрическая фигура, которая представляет собой четырехугольник, а конкретно параллелограмм (фигура, у которой противоположные стороны равны и параллельны). Но параллелограмм не обычный, а с особенностями. У него все стороны пересекаются друг с другом под прямым углом.
Выглядит прямоугольник соответственно:
А частным случаем прямоугольника является квадрат:
У такого прямоугольника стороны не только пересекаются под прямым углом, но и равны между собой.
Как и многие термины в математике, жир слово пришло к нам из Древней Греции. Дословно оно означает «περιμετρέο» — «окружность» или «измерять вокруг». Таким образом,
Периметр – это совокупная длина границ любой геометрической фигуры. Этим словом обозначают как сами границы, так и их математическое значение.
С этим словом мы часто встречаемся в повседневной жизни. Например, когда нужно поставить забор на дачном участке, то его устанавливают по периметру участка. И мы понимаем, что речь идет о границах.
Также, солдаты или полицейские часто стоят в оцеплении «по периметру» какой-то территории. А кулинары часто украшают торт фруктами или кремовыми цветами также «по периметру».
Как найти периметр прямоугольника
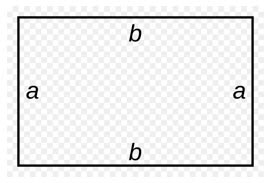
Возьмем для примера такой прямоугольник:
Исходя из общего определения, чтобы посчитать периметр прямоугольника, надо просто сложить все его стороны.
Периметр в математике обозначается латинской буквой «Р». И соответственно формула выглядит так:
С учетом равенства сторон, формулы можно существенно упростить:
или
Предположим, что у нас длина прямоугольника равна 4 сантиметрам, а ширина 2. Тогда периметр этой геометрической фигуры составит:
И тут появляется важное замечание. Периметр измеряется в тех же величинах, что и длины сторон прямоугольника. Это могут быть миллиметры, сантиметры, метры, километры и так далее.
В случае с квадратом, который, напомним, является частным случаем прямоугольника, посчитать периметр еще проще. Благодаря тому, что у него все стороны равны (назовем их условно «а»), формула выглядит так:
или
Опять же приведем конкретный пример. Если возьмем квадрат со стороной 4 сантиметра, то его периметр составит P = 4 * 4 = 16 сантиметров.
Другие формулы для расчета периметра прямоугольника
Иногда школьникам предлагают такую задачу – нужно вычислить периметр прямоугольника, зная его площадь и длину одной стороны.
Тут надо знать, как вычисляется сама площадь. Для этого надо просто перемножить длины двух сторон:
Соответственно, мы можем определить длину недостающей нам стороны. Для этого надо просто разделить площадь на другую сторону:
Таким образом, мы у нас будут значения обеих сторон прямоугольника. А уже после периметр вычисляется по стандартной формуле.
Бывают и более сложные задачи по нахождению периметра прямоугольники, например, как в приведенном ниже видео:
Вместо заключения
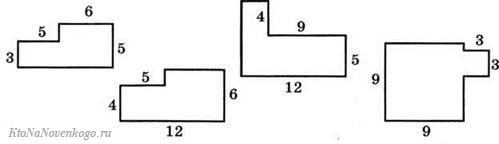
Зная длины сторон, можно вычислять и периметры более сложных прямоугольных фигур. Вот таких:
Страшно выглядят они только на первый взгляд. А на деле, надо просто провести недостающую линию и разделить каждую из фигур на два прямоугольника. Далее вычисляем их по отдельности и складываем друг с другом. Как результат – общий периметр фигуры.
Вот и все, что мы хотели сегодня рассказать.