Содержание:
- Формула
- Примеры вычисления периметра прямоугольного треугольника
Формула
Чтобы найти периметр прямоугольного треугольника нужно найти сумму длин его сторон.
Таким образом, если $ABC$ – прямоугольный треугольник, в
котором
$a$ и
$b$ – длинны катетов, а
$c$ – длина гипотенузы, то периметр находится по формуле:
$$P_{Delta A B C}=a+b+c$$
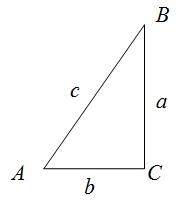
Примеры вычисления периметра прямоугольного треугольника
Пример
Задание. В прямоугольном треугольнике катеты равны 3 дм и 4 дм, а гипотенуза –
5 дм. Найти его периметр.
Решение. Найдем периметр этого треугольника по формуле
$$P_{Delta A B C}=a+b+c$$
Подставляя заданные длины сторон, получим:
$P_{Delta A B C}=a3+4+5=12$ (дм)
Ответ. $P_{Delta A B C}=12$ (дм)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. В прямоугольном треугольнике
$ABC$ длина гипотенузы и одного из катетов соответственно равны
13 м и 12 м. Найти периметр $Delta A B C$.
Решение. Введем обозначение
$a$ и
$b$ – дины катетов,
$c$ – длина гипотенузы. По условию
$c=13$ м и
$a=12$ м. Длину
$b$ второго катета найдем по теореме Пифагора:
$$b=sqrt{c^{2}-a^{2}}$$
Подставляя заданные длины сторон, получим
$b=sqrt{13^{2}-12^{2}}=sqrt{169-144}=sqrt{25}=5$ (м)
Теперь по формуле
$$P_{Delta A B C}=a+b+c$$
можем найти искомый периметр:
$P_{Delta A B C}=13+12+5=30$ (м)
Ответ. $P_{Delta A B C}=30$ (м)
Читать дальше: как найти периметр равнобедренного треугольника.
Выбирайте формулу в зависимости от известных величин.
1. Как найти периметр треугольника, зная три стороны
Просто посчитайте сумму всех сторон.
- P — искомый периметр;
- a, b, c — стороны треугольника.
2. Как найти периметр треугольника, зная его площадь и радиус вписанной окружности
Умножьте площадь треугольника на 2.
Разделите результат на радиус вписанной окружности.
- P — искомый периметр;
- S — площадь треугольника;
- r — радиус вписанной окружности.
3. Как вычислить периметр треугольника, зная две стороны и угол между ними
Сначала найдите неизвестную сторону треугольника с помощью теоремы косинусов:
- Умножьте одну сторону на вторую, на косинус угла между ними и на 2.
- Посчитайте сумму квадратов известных сторон и отнимите от неё число, полученное в предыдущем действии.
- Найдите корень из результата.
Теперь прибавьте к найденной стороне две ранее известные стороны.
- P — искомый периметр;
- b, c — известные стороны треугольника;
- ɑ — угол между известными сторонами;
- a — неизвестная сторона треугольника.
4. Как найти периметр равностороннего треугольника, зная одну сторону
Умножьте сторону на 3.
- P — искомый периметр;
- a — любая сторона треугольника (напомним, в равностороннем треугольнике все стороны равны).
5. Как вычислить периметр равнобедренного треугольника, зная боковую сторону и основание
Умножьте боковую сторону на 2.
Прибавьте к результату основание.
- P — искомый периметр;
- a — боковая сторона треугольника (в равнобедренном треугольнике боковые стороны равны);
- b — основание треугольника (это сторона, которая отличается длиной от остальных).
6. Как найти периметр равнобедренного треугольника, зная боковую сторону и высоту
Найдите квадраты боковой стороны и высоты.
Отнимите от первого числа второе.
Найдите корень из результата и умножьте его на 2.
Прибавьте к полученному числу две боковые стороны.
- P — искомый периметр;
- a — боковая сторона треугольника;
- h — высота (перпендикуляр, опущенный на основание треугольника со стороны противоположной вершины; в равнобедренном треугольнике высота делит основание пополам).
7. Как вычислить периметр прямоугольного треугольника, зная катеты
Найдите квадраты катетов и посчитайте их сумму.
Извлеките корень из полученного числа.
Прибавьте к результату оба катета.
- P — искомый периметр;
- a, b — катеты треугольника (стороны, которые образуют прямой угол).
8. Как найти периметр прямоугольного треугольника, зная катет и гипотенузу
Посчитайте квадраты гипотенузы и катета.
Отнимите от первого числа второе.
Найдите корень из результата.
Прибавьте катет и гипотенузу.
- P — искомый периметр;
- a — любой катет прямоугольника;
- c — гипотенуза (сторона, которая лежит напротив прямого угла).
Многим формулам поиска периметра учат в 3 классе. Это фундаментальные знания, которые будут пригождаться на протяжении всех лет обучения в школе, и даже в вузе при выборе математического факультета. В этой статьем рассмотрим, как находить периметр треугольника.
Определение
Периметром принято называть сумму длин всех сторон многоугольника. Периметр обозначается заглавной латинской буквой P. Под P удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах и ходе решении.
Важно, чтобы все значения были заданы в одной единице измерения длины, иначе мы не сможем подсчитать результат. Поэтому для правильного решения необходимо привести все данные к одной единице измерения.
Часто встречающиеся единицы измерения периметра:
-
миллиметр (мм);
-
сантиметр (см);
-
дециметр (дм);
-
метр (м);
-
километр (км).
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас

Как узнать периметр треугольника
Рассмотрим, какие существуют формулы и при каких известных исходных данных их можно применять.
-
Если известны три стороны, то периметр треугольника равен сумме их длин.
Этот способ обычно проходят во втором классе.
P = a + b + c, где a, b, c — длина стороны.
-
Если известна площадь и радиус вписанной окружности:
P = 2S / r, где S — площадь, r — радиус вписанной окружности.
-
Если известна одна сторона в равностороннем треугольнике:
P = 3a, где a — длина стороны.
Все стороны в равносторонней фигуре равны.
-
Если известна боковая сторона и основание в равнобедренном треугольнике:
P = 2a + b, где a — боковая сторона, b — основание.
Боковые стороны в равнобедренном треугольнике равны.
-
Если известна боковая сторона и высота в равнобедренном треугольнике:
, где a — боковая сторона, h — высота, проведенная к основанию.
Высота — перпендикуляр, опущенный из вершины треугольника на противолежащую сторону. В равнобедренном треугольнике, высота, проведенная к основанию, является медианой, т. е. делит сторону пополам.
-
Если известны катеты в прямоугольном треугольнике:
, где a, b — катеты.
Катет — одна из двух сторон, которые образуют прямой угол.
-
Если известны катет и гипотенуза в прямоугольном треугольнике:
, где a — любой катет, c — гипотенуза.
Гипотенуза — сторона, которая лежит напротив прямого угла.
Скачать онлайн таблицу
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
Шпаргалки для родителей по математике
Все формулы по математике под рукой

Периметр прямоугольного треугольника


4.3
Средняя оценка: 4.3
Всего получено оценок: 75.
4.3
Средняя оценка: 4.3
Всего получено оценок: 75.
Нахождение периметра прямоугольного треугольника мало чем отличается от нахождения периметра любой другой фигуры. Здесь не существует специализированной формулы, разница только лишь в подходах к решению задач.
Формула для нахождения периметра прямоугольного треугольника
Как уже говорилось ранее, специализированных формул периметра прямоугольного треугольника нет. Чтобы найти периметр нужно просто просуммировать длины всех трех сторон.
Но для треугольника действуют тригонометрические отношения, теорема Пифагора и ряд специальных формул площади. Эти формулы открывают целый набор подходов к решению задач, которые не характерны для произвольной фигуры. Рассмотрим несколько вариантов нахождения периметра прямоугольного треугольника.
Задача 1
- В прямоугольном треугольнике площадь равняется 24, а один из катетов равен 6. Найти периметр треугольника.
Площадь прямоугольного треугольника можно найти как половину произведения катетов. Значение площади уже есть, значит, нужно найти второй катет и гипотенузу. Обозначим катеты латинскими буквами a и b, а гипотенузу буквой c. Пусть а=6.
Тогда: $$S={1over 2}*a*b=24$$
$$S={1over 2}*6*b=24$$
$$3b=24$$
b=8
Две из трех сторон известны, а гипотенузу всегда можно найти через теорему Пифагора.
$$c^2=a^2+b^2$$
$$c=sqrt{a^2+b^2}$$
$$c=sqrt{36+64}=10$$
Найдем периметр, как сумму длин всех сторон:
P=a+b+c=10+8+6=24
Задача 2
- В прямоугольном треугольнике АВС катет АВ=8, а острый угол равен 30 градусам. Найти периметр прямоугольного треугольника.
Если в задаче дается острый угол прямоугольного треугольника, значит в любом случае в решении нужно использовать тригонометрические функции. Иначе для нахождения результата просто не хватит данных.
В этой задаче есть два возможных варианта. Острый угол может быть расположен у известного катета, а может противолежать ему. В любом случае придется использовать тригонометрические функции, но результаты могут разница. Обычно в задаче этот момент прописывается, но иногда от решающего требуется предоставить оба варианта решения. Это ясно из условия, в котором не говорится, какой из острых углов дан.
Рассмотрим вариант, при котором дан острый угол при известном катете. Тогда воспользуемся функцией косинуса:
$$Cos(BAC)={ABover AC}={sqrt{3}over2}$$
$$AC={ABover {cos(BAC)}}$$
$$AC={8over{sqrt{3}over 2}}={16oversqrt{3}}=9,24$$ – значение округлим до сотых
BC найдем через значение тангенса.
$$tg(BAC)={BCover AB}={1oversqrt{3}}$$
$$BC=AB*{1oversqrt{3}}={ABoversqrt{3}}$$
$$BC={8oversqrt{3}}=4,62$$
Вычисление периметра произведем по общей формуле:
P=8+9,24+4,62=21,86
Если острый угол противолежит известному катету, то решение будет выглядеть немного иначе.
Найдем BC через значение тангенса.
$$tg(ACB)={ABover BC}={1oversqrt{3}}$$
$$BC={ABover {1oversqrt{3}}}=AB*sqrt{3}=8*sqrt{3}=13,86$$
Гипотенузу найдем через значение синуса.
$$sin(ACB)={ABover AC}={1over 2}$$
$$AC={ABover sin(ACB)}={ABover {1over 2}}=2*AB=2*8=16$$
Если в расчетах присутствуют округления, то лучше округленный результат не использовать в дальнейших вычислениях. То есть, если мы посчитали BC, то AC лучше найти через синус, а не через косинус или теорему Пифагора, если есть такая возможность. Использование точных значений избавляет от больших погрешностей в результатах.

Что мы узнали?
Мы узнали, что отличия между формулой периметра для прямоугольного и произвольного треугольника нет. Разница в пути решения. Найти периметр прямоугольного треугольника можно через теорему Пифагора, площадь или тригонометрические функции, можно комбинировать различные методы между собой. Главное, это возможность решения задачи без дополнительных построений.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка статьи
4.3
Средняя оценка: 4.3
Всего получено оценок: 75.
А какая ваша оценка?
Содержание материала
- Как найти периметр прямоугольного треугольника
- Видео
- Прямоугольный треугольник в реальности
- Что мы узнали?
- Как узнать периметр треугольника
- Второй метод: прямоугольный треугольник и две известные его стороны
- Примеры решения задач
- Задача
- Задача
- Задача
- Задача
- Задача
Как найти периметр прямоугольного треугольника
Чтобы узнать как найти периметр прямоугольного треугольника, нужно вспомнить что такое периметр.Для того, чтобы найти периметр нужно сложить все длины сторон данного треугольника.Например, если МТЕ — прямоугольный треугольник, и он имеет катеты и и гипотенузу , то его периметр будет равен:
Рассмотрим примеры того, как найти периметр треугольника с прямым углом.
Пример 1.У прямоугольного треугольника гипотенузы равна 19 дм, а катеты соответственно по 13 дм и 17 дм. Найдем периметр этого треугольника.
Решение.Воспользуемся формулой для нахождения периметра прямоугольного треугольника:
Подставим известные значения и получим: (дм).
Ответ. (дм).
Пример 2.Известны гипотенуза и катет прямоугольного треугольника, длины которых равны соответственно 31 см и 23 см. Найдем периметр заданного треугольника.
Решение.Согласно условию дан прямоугольный треугольник, у которого есть две известные длины — длина гипотенузы и длина катета. Для того, чтобы найти периметр заданного треугольника, необходимо знать и длину второго катета. Поскольку треугольник является прямоугольным, то мы можем воспользоваться теоремой Пифагора, из которой и найдем неизвестную длину:
(см).Найдем периметр согласно рассмотренной выше формуле: (см).
Ответ. (см).
ru.solverbook.com
Видео
Прямоугольный треугольник в реальности
Непосредственно прямоугольный треугольник встречается в реальности на каждом углу, как в прямом, так и в переносном смысле. Форму прямоугольного треугольника имеют грани тетраэдров и призм, которые в реальности превращаются в детали машин, керамическую плитку или скаты крыш. Угольник — чертежный инструмент, с которым человек впервые встречается на уроке геометрии, имеет форму именно прямоугольного треугольника и используется в проектировании, строительстве и столярном деле.
Что мы узнали?
Мы узнали, что отличия между формулой периметра для прямоугольного и произвольного треугольника нет. Разница в пути решения. Найти периметр прямоугольного треугольника можно через теорему Пифагора, площадь или тригонометрические функции, можно комбинировать различные методы между собой. Главное, это возможность решения задачи без дополнительных построений.
Как узнать периметр треугольника
Рассмотрим, какие существуют формулы и при каких известных исходных данных их можно применять.
-
Если известны три стороны, то периметр треугольника равен сумме их длин.
Этот способ обычно проходят во втором классе.
P = a + b + c, где a, b, c — длина стороны.

-
Если известна площадь и радиус вписанной окружности:
P = 2S / r, где S — площадь, r — радиус вписанной окружности.

-
Если известна одна сторона в равностороннем треугольнике:
P = 3a, где a — длина стороны.
Все стороны в равносторонней фигуре равны.

-
Если известна боковая сторона и основание в равнобедренном треугольнике:
P = 2a + b, где a — боковая сторона, b — основание.
Боковые стороны в равнобедренном треугольнике равны.

-
Если известна боковая сторона и высота в равнобедренном треугольнике:
, где a — боковая сторона, h — высота, проведенная к основанию.
Высота — перпендикуляр, опущенный из вершины треугольника на противолежащую сторону. В равнобедренном треугольнике, высота, проведенная к основанию, является медианой, т. е. делит сторону пополам.

-
Если известны катеты в прямоугольном треугольнике:
, где a, b — катеты.
Катет — одна из двух сторон, которые образуют прямой угол.

-
Если известны катет и гипотенуза в прямоугольном треугольнике:
, где a — любой катет, c — гипотенуза.
Гипотенуза — сторона, которая лежит напротив прямого угла.

Второй метод: прямоугольный треугольник и две известные его стороны
 В том случае, когда в задании, которое нужно решить, дана прямоугольная фигура, длины двух граней которой известны, а третья нет, необходимо воспользоваться теоремой Пифагора.
В том случае, когда в задании, которое нужно решить, дана прямоугольная фигура, длины двух граней которой известны, а третья нет, необходимо воспользоваться теоремой Пифагора.
Теорема Пифагора описывает соотношение между гранями прямоугольного треугольника. Формула, описываемая этой теоремой, является одной из самых известных и наиболее часто применяемых теорем в геометрии. Итак, сама теорема:
Стороны любого прямоугольного треугольника описываются таким уравнением: a^2 + b^2 = c^2, где а и b — катеты фигуры, а c — гипотенуза.
- Гипотенуза. Она всегда расположена противоположно прямому углу (90 градусов), а также является самой длинной гранью треугольника. В математике принято обозначать гипотенузу буквой c.
- Катеты — это грани прямоугольного треугольника, которые относятся к прямому углу и обозначаются буквами а и b. Один из катетов одновременно является и высотой фигуры.
Таким образом, если условиями задачи заданы длины двух из трех граней такой геометрической фигуры, с помощью теоремы Пифагора необходима найти размерность третьей грани, после чего воспользоваться формулой из первого метода.
Например, мы знаем длину 2-х катетов: a = 3 см, b = 5 см. Подставляем значения в теорему: 3^2 + 4^2 = c^2 => 9 + 16 = c^2 => 25 = c^2 => c = 5 см. Итак, гипотенуза такого треугольника равна 5 см. К слову, данный пример является самым распространенным и называется «Египетский треугольник». Иными словами, если два катета фигуры равны 3 см и 4 см, то гипотенуза составит 5 см соответственно.
Если неизвестна длина одного из катетов, необходимо преобразовать формулу следующим образом: c^2 — a^2 = b^2. И наоборот для другого катета.
Продолжим пример. Теперь необходимо обратиться к стандартной формуле поиска периметра фигуры: P = a + b + c. В нашем случае: P = 3 + 4 + 5 = 12 см.
Примеры решения задач
Для тренировки полученных знаний, рассмотрим несколько примеров решения задач на поиск периметра треугольника.
Задача
Какой P треугольника, если его стороны равны 6 см, 7 см и 3 см.
Решение:
Подставляем в формулу P = a+b+c известные величины и получаем: P = 6+7+3=16 см.
Ответ: 16 см.
Задача
Известно, что основание равнобедренного треугольника равно 6 см, а его боковая сторона — 4 см. Найти P фигуры.
Решение:
Для данного случая подходит формула P=a+2b, подствляем значения: (P=6+4times2 = 14) см.
Ответ: 14 см.
Задача
Нам известно, что площадь треугольника — 24 см2, а радиус вписанной в него окружности — 8 см. Найти P.
Решение:
В данном случае рассчитывать P будем следующим образом: (P=frac{2S}r). С уже известными нам величинами получаем: (P=frac{2times24}8 = 6) см.
Ответ: 6 см.
Задача
Дан равнобедренный треугольник. Нам известна его боковая сторона (4 см) и высота, опущенная к основанию (2 см). Нужно вычислить периметр фигуры.
Решение:
Мы знаем, что в этом случае P вычисляется, как (P=2sqrt{a^2-h^2}+2a). С имеющимися значениями получается: (P=2sqrt{4^2-2^2}+2times2 = 4sqrt3+4) см.
Ответ: P=4sqrt3+4 см.
Задача
Дан прямоугольный треугольник с катетами 5 см и 7 см. Определить периметр фигуры.
Решение:
В формулу (P=sqrt{a^2+b^2}+a+b) подставляем известные значения: (P=sqrt{5^2+7^2}+5+7 = sqrt{74}+12) см.
Ответ: (P=sqrt{74}+12) см.
