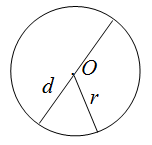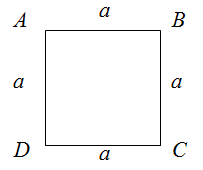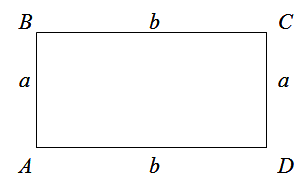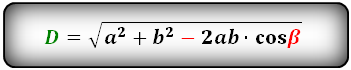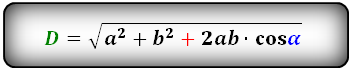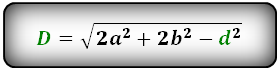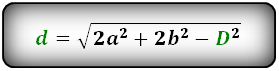Как найти периметр равнобедренного параллелограмма

Что такое периметр параллелограмма

Периметр параллелограмма — это сумма длин всех его сторон.

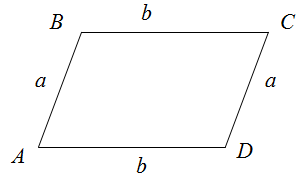
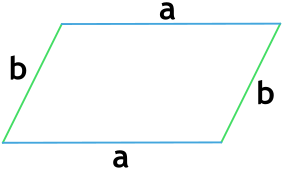
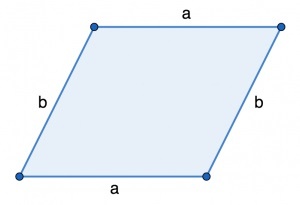
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно равны и параллельны друг другу. Таким образом, его периметр — это удвоенная сумма двух его смежных ребер.

Свойства

• противоположные стороны равны и параллельны;
• противоположные углы попарно равны;
• сумма соседних углов равна 180 градусов;
• сумма всех углов равна 360 градусов;
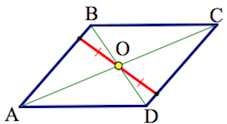
• диагонали фигуры делятся пополам в точке пересечения;
• точка пересечения диагоналей — центр симметрии параллелограмма;

• биссектриса образует равнобедренный треугольник.

Как найти периметр

Существует несколько основных способов, с помощью которых можно найти сумму длин всех сторон заданной фигуры. Все они зависят от изначально известных параметров.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

По сумме всех сторон

Так как периметр параллелограмма — это удвоенная сумма двух его смежных ребер, используем  формулу:

P=2(a+b),

где a и b — это две смежные стороны данного четырехугольника.

По стороне и двум диагоналям

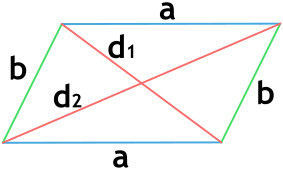
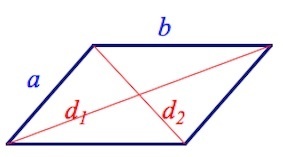
Если в задаче дана лишь одна сторона, но обе диагонали четырехугольника, мы можем найти вторую сторону. Для этого используем формулу:

(a=frac{sqrt{2d_1^2+2d_2^2-4b^2}}2,)

где (d_1) и (d_2) — это обе диагонали фигуры.

Получается, что расчет суммы длин всех сторон для параллелограмма будет выглядеть так:

(P=2(frac{sqrt{2d_1^2+2d_2^2-4b^2}}2+b).)

По стороне, высоте и синусу угла

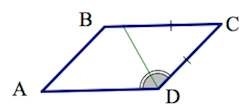
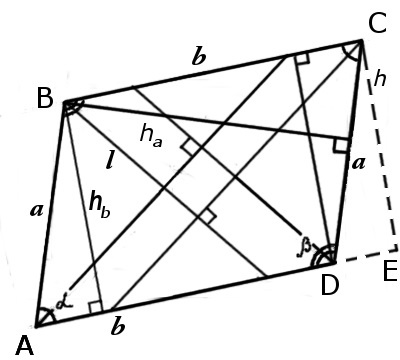
В случае, если нам известны лишь одно ребро, высота и один из углов, можем узнать длину второго ребра таким образом:

(a=frac{h_b}{sinalpha})

где (h_b) — высота, проведенная к известной стороне, а (sinalpha) — известный нам угол.

Таким образом, формула для нахождения периметра параллелограмма будет выглядеть так:

(P=2(frac{h_b}{sinalpha}+b))

Примеры решения задач

Попробуем применить полученные знания на практике и рассмотрим несколько задач на периметр параллелограмма.

Задача 1

Дан параллелограмм со сторонами 5 см и 9 см. Вычислить его периметр.

Решение:

Воспользуемся формулой P=2(a+b), так как нам известны обе стороны фигуры. Подставляем значения: P=2(5+9)=28 см.

Ответ: 28 см.

Задача 2

Известно, что одна из сторон параллелограмма равна 4 см, а две его диагонали равны 6 см и 8 см. Найти периметр фигуры.

Решение:

Для расчета суммы длин всех сторон используем формулу:

(P=2(frac{sqrt{2d_1^2+2d_2^2-4b^2}}2+b))

Подставляем известные значения:

(P=2(frac{sqrt{2d_1^2+2d_2^2-4b^2}}2+b)=2(frac{sqrt{2times6^2+2times8^2-4times4^2}}2+4)=2(frac{sqrt{72+128-64}}2+4)=2(frac{2sqrt{34}}2+4)=2sqrt{34}+8) см.

Ответ:( 2sqrt{34}+8) см.

Задача 3

Сторона b параллелограмма равна 2 см, высота, проведенная к b — 1 см, а угол α равен (fracpi6). Найти сумму длин всех сторон фигуры.

Решение:

Для расчета будем использовать уравнение:

(P=2(frac{h_b}{sinalpha}+b))

Подставим известные величины:

(P=2(frac1{sin{displaystylefracpi6}}+2)=2(frac1{displaystylefrac12}+2)=8;)см.

Ответ: 8 см.

В данной публикации мы рассмотрим, каким образом можно посчитать периметр параллелограмма и разберем примеры решения задач.

• Формула вычисления периметра

• Примеры задач

Формула вычисления периметра

Периметр (P) параллелограмма равняется сумме длин всех его сторон. А т.к. противоположные стороны данной фигуры равны, формулу можно представить в следующем виде:

P = 2 * (a + b) или P = 2a + 2b

Примеры задач

Задание 1
Найдите периметр параллелограмма, если его стороны равны 6 и 8 см.

Решение:
Воспользуемся одной из двух формул выше, подставив в нее известные значения: P = 2 * 6 см + 2 * 8 см = 28 см.
Тот же самый результат получится, если применить вторую формулу: P = 2 * (6 см + 8 см) = 28 см.

Задание 2
Периметр параллелограмма равен 50 см. Найдите его вторую сторону, если известно, что первая равна 7 см.

Решение:
Нам известно, что периметр считается по формуле: P = 2a + 2b.
Допустим a – это известная сторона, и нам нужно найти b. Ее длина, умноженная на два, равна: 2b = P – 2a = 50 см – 2 * 7 см = 36 см.
Следовательно, длина неизвестной стороны составляет: b = 36 см / 2 = 18 см.

Содержание:

• Определения
• Формулы периметра основных геометрических фигур

Определения

Периметр имеет ту же размерность величин, что и длина. Иногда периметром называют границу геометрической фигуры.
Чаще всего этот термин применяется к треугольнику и многоугольникам и в этом случае означает сумму длин всех сторон фигуры.
То есть периметр – это сумма длин сторон какой-либо геометрической фигуры.

Формулы периметра основных геометрических фигур

Периметр треугольника

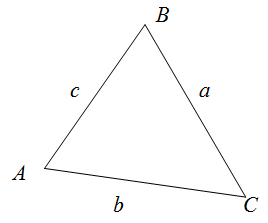
Чтобы найти периметр треугольника $ABC$,
необходимо сложить длины всех его сторон.

Читать дальше: формула периметра треугольника и примеры решений →

Периметр круга

Чтобы найти периметр круга, необходимо вычислить длину окружности, которая его ограничивает.

Для нахождения длины окружности можно использовать одну из формул

Читать дальше: формула периметра круга и примеры решений →

Периметр квадрата

Чтобы найти периметр квадрата, необходимо длину его стороны умножить на четыре.

Читать дальше: формула периметра квадрата и примеры решений →

Периметр прямоугольника

Чтобы найти периметр прямоугольника, нужно сумму его ширины и длины умножить на два.

Читать дальше: формула периметра прямоугольника и примеры решений →

Периметр параллелограмма

Чтобы найти периметр параллелограмма, нужно сумму двух непараллельных сторон умножить на два.

Читать дальше: формула периметра параллелограмма и примеры решений →

Периметр трапеции

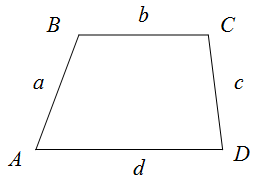
Чтобы найти периметр трапеции необходимо найти сумму длин её сторон.

Читать дальше: формула периметра трапеции и примеры решений →

Периметр ромба

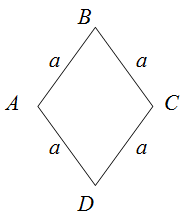
Чтобы найти периметр ромба, необходимо длину его стороны умножить на четыре.

Читать дальше: формула периметра ромба и примеры решений →

Периметр эллипса

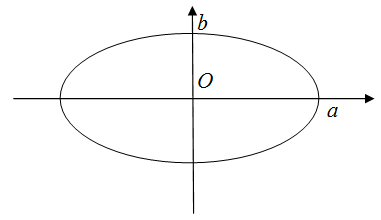
Чтобы найти периметр эллипса
$frac{x^{2}}{a^{2}}+frac{y^{2}}{b^{2}}=1$, нужно воспользоваться формулой

Читать дальше: формула периметра эллипса и примеры решений →

• Как найти периметр треугольника
• Как найти периметр трапеции
• Как найти периметр ромба
• Как найти периметр эллипса
• Как найти периметр многоугольника
• Как найти периметр прямоугольного треугольника
• Как найти периметр равнобедренного треугольника
• Как найти периметр равностороннего треугольника
• Как найти периметр круга
• Как найти длину окружности
• Как найти периметр квадрата
• Как найти периметр прямоугольника
• Как найти периметр параллелограмма

Периметр параллелограмма зависит от длины его сторон. И хотя формула для расчета несложная, мы сделали калькулятор, который позволяет рассчитать периметр параллелограмма в режиме онлайн. Наш калькулятор рассчитает периметр параллелограмма по двум сторонам или по двум диагоналям и одной из сторон.

На сайте вы можете рассчитать периметры других четырехугольников: квадрат, ромб, прямоугольник.

Формула периметра параллелограмма через две стороны

Формула периметра параллелограмма через диагонали и сторону

Примеры задач на нахождение периметра параллелограмма

Формула нахождения периметра параллелограмма

Что такое периметр параллелограмма

Периметр параллелограмма — это сумма длин всех его сторон.

Параллелограмм — это четырехугольник, у которого противоположные стороны попарно равны и параллельны друг другу. Таким образом, его периметр — это удвоенная сумма двух его смежных ребер.

Свойства

• противоположные стороны равны и параллельны;
• противоположные углы попарно равны;
• сумма соседних углов равна 180 градусов;
• сумма всех углов равна 360 градусов;
• диагонали фигуры делятся пополам в точке пересечения;
• точка пересечения диагоналей — центр симметрии параллелограмма;

Как найти периметр

Существует несколько основных способов, с помощью которых можно найти сумму длин всех сторон заданной фигуры. Все они зависят от изначально известных параметров.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

По сумме всех сторон

Так как периметр параллелограмма — это удвоенная сумма двух его смежных ребер, используем формулу:

где a и b — это две смежные стороны данного четырехугольника.

По стороне и двум диагоналям

Если в задаче дана лишь одна сторона, но обе диагонали четырехугольника, мы можем найти вторую сторону. Для этого используем формулу:

где (d_1) и (d_2) — это обе диагонали фигуры.

Получается, что расчет суммы длин всех сторон для параллелограмма будет выглядеть так:

По стороне, высоте и синусу угла

В случае, если нам известны лишь одно ребро, высота и один из углов, можем узнать длину второго ребра таким образом:

где (h_b) — высота, проведенная к известной стороне, а (sinalpha) — известный нам угол.

Таким образом, формула для нахождения периметра параллелограмма будет выглядеть так:

Примеры решения задач

Попробуем применить полученные знания на практике и рассмотрим несколько задач на периметр параллелограмма.

Задача 1

Дан параллелограмм со сторонами 5 см и 9 см. Вычислить его периметр.

Решение:

Воспользуемся формулой P=2(a+b), так как нам известны обе стороны фигуры. Подставляем значения: P=2(5+9)=28 см.

Задача 2

Известно, что одна из сторон параллелограмма равна 4 см, а две его диагонали равны 6 см и 8 см. Найти периметр фигуры.

Решение:

Для расчета суммы длин всех сторон используем формулу:

Подставляем известные значения:

Ответ: ( 2sqrt<34>+8) см.

Задача 3

Сторона b параллелограмма равна 2 см, высота, проведенная к b — 1 см, а угол α равен (fracpi6) . Найти сумму длин всех сторон фигуры.

Источник

Как найти периметр фигуры

О чем эта статья:

Определение периметра

Периметром принято называть длину всех сторон многоугольника. Какой буквой обозначается периметр — заглавной латинской P. Под обозначением «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.

Если параметры переданы в разных единицах длины, мы не сможем узнать какая площадь фигуры получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

В чем измеряется периметр:

Формула нахождения периметра

Рассмотрим пять фигур.

Треугольник

Периметр треугольника — это сумма длин трех его сторон.

P = a + b + c, где a, b, c — длина стороны.

Формула измерения периметра для равностороннего треугольника — это произведение длины стороны на три.

P = 3 * a, где a — длина стороны.

Квадрат и ромб

Периметр квадрата — это произведение длины стороны на четыре. Формула ромба выглядит идентично.

P = 4 * a, где a — длина стороны.

Прямоугольник и параллелограмм

Периметр прямоугольника — сумма длины и ширины, умноженная на два. Формула параллелограмма выглядит соответственно.

P = 2 * (a + b), где a — ширина, b — высота.

Записывайтесь на онлайн уроки по математике к лучшим преподавателям! Уроки для учеников с 1 по 11 классы!

Равнобедренная трапеция

Формула для равнобедренной трапеции отличается от прямоугольника тем, что у первого есть две равные стороны.

P = a + b + 2 * c, где a, b — параллельные стороны, c — две длины одинаковых сторон.

Периметр круга или длина окружности — это произведение радиуса на два Пи или произведение диаметра на Пи.

L = d * π = 2 * r * π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Можно выучить все формулы, а можно, запомнив определение о сумме всех сторон, каждый раз проявлять смекалку и вычислять самостоятельно. Давайте потренируемся, как определять периметр фигур!

Решение задач

Площадь прямоугольника равна 80 см 2 , длина составляет 10 см. Чему равен периметр фигуры?

• Для использования формулы P = 2 * (a + b), нам нужно найти ширину;
• Так как S = a * b, для поиска одной стороны необходимо разделить площадь на известную сторону: 80 : 10 = 8 см;
• Далее подставляем известные переменные в формулу: (10 + 8) * 2 = 36 см;

Равнобедренный треугольник имеет периметр 40 см, длина его основания составляет 6 см. Какую длину будут иметь две другие стороны?

• Используя формулу P = a + b + c вычислим сумму двух неизвестных сторон: 40 — 6 = 34 см;
• Известно, что равнобедренный треугольник имеет две равные стороны;
• Далее делим получившуюся сумму на два: 34 : 2 = 17 см;

Ответ: две другие стороны равны 17см.

Круг вписан в квадрат, его сторона равна 20 см. Найти периметр круга.

• Периметр круга равен длине ограничивающей его окружности. Значит P = L = d * π;
• Сторона квадрата для круга является диаметром, поэтому P = 20 * 3,14;

Источник

Калькулятор периметра параллелограмма через диагонали

Параллелограмм — четырехугольник, стороны которого являются попарно параллельными отрезками. Параллелограмм представляет собой фигуру, частными случаями которой являются ромб, прямоугольник и квадрат — четырехугольники, знакомые нам с самого детства.

Геометрия параллелограмма

Четырехугольник считается параллелограммом, если соблюдается хотя бы одно из нижеперечисленных условий:

• противоположные стороны параллельны друг другу;
• противоположные стороны равны друг другу;
• пересекающиеся диагонали в точке пересечения делятся пополам.

Параллелограмм и его частные случаи — наиболее встречающаяся в реальной жизни фигура. В трехмерном пространстве параллелограмм превращается в четырехугольную призму, форму которой имеет большинство рукотворных объектов: кирпичи, системные блоки компьютеров, стены, книги или коробки. Косоугольные фигуры встречаются реже, однако форму таких параллелограммов имеют грани резцов металлообрабатывающих станков или элементы дизайна и декора, такие как ковры или геометрические узоры на стенных покрытиях.

Параллелограмм также можно увидеть прямо на улице. Прямоугольные или косоугольные окна — это параллелограммы. Кроме того, прямо под ногами вы можете увидеть один из наиболее банальных воплощений ромба в реальности — тротуарную плитку. Столь широкое распространение данной фигуры в повседневной жизни делает вопрос определения площади и периметра параллелограмма актуальной задачей.

Периметр параллелограмма

Периметр представляет собой количественную оценку общей длины сторон любой фигуры. Параллелограмм имеет четыре стороны, которые попарно равны и параллельны друг другу. Исходя из этого, периметр геометрической фигуры выражается простой формулой:

Путем подстановок мы можем найти стороны геометрической фигуры при помощи диагоналей и одной из ее высот. Наш онлайн-калькулятор позволяет определить периметр параллелограмма, зная три переменных: две диагонали и высоту четырехугольника.

Естественно, что вы можете воспользоваться и самой простой формулой для подсчета периметра, однако программный код калькулятора требует введения 3 переменных, поэтому для его корректной работы помимо длин сторон введите значение высоты, равное ha = b или hb = a. К примеру, если a = 3, b = 4, то укажите, что hb = 3 или ha = 4. Такая подстановка превратит параллелограмм в квадрат, однако при известных сторонах периметр не зависит от величины углов геометрической фигуры, что позволит нам корректно рассчитать требуемый параметр. Рассмотрим пару примеров.

Примеры из жизни

Пример №1

Давайте определим периметр четырехугольника, зная, что его диагонали равны 3 и 5 см, а высота фигуры составляет 2 см. Свойства четырехугольника подсказывают нам, что высота численно не может быть больше длин диагоналей, поэтому параметр h всегда меньше и d1, и d2. Введем эти данные в форму калькулятора и получим мгновенный ответ:

Зная эти переменные, мы можем определить периметр любого параллелограмма.

Пример №2

Определить периметр абстрактного параллелограмма можно и по стандартной, самой простой формуле. Если стороны четырехугольника равны a = 3 и b = 4, то нам понадобится ввести эти данные в калькулятор, а также указать, что ha = 4. Мы получим ответ в виде:

что полностью соответствует расчетам по классической формуле P = 2 (a + b).

Заключение

Параллелограмм и его частные случаи занимают в деятельности человека важное место. В реальной жизни вам понадобится определять периметры и площади прямоугольников, квадратов, ромбов или параллелограммов, которые являются гранями соответствующих призм или полноценными фигурами на плоскости. Используйте наши калькуляторы для выполнения расчетов при решении повседневных, школьных или профессиональных задач.

Источник

Как найти периметр параллелограмма через диагонали

Признаки параллелограмма

AB||CD, AB = CD (или BC||AD, BC = AD)

∠DAB = ∠BCD, ∠ABC = ∠CDA

∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°

AC 2 + BD 2 = AB 2 + BC 2 + CD 2 + AD 2

Основные свойства параллелограмма

∠ABC = ∠CDA, ∠BCD = ∠DAB

∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°

∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°

8. Диагонали параллелограмма пересекаются и точкой пересечения делят друг друга пополам:

AO = CO =	d 1
2
BO = DO =	d 2
2

AC 2 + BD 2 = 2AB 2 + 2BC 2

Стороны параллелограмма

Формулы определения длин сторон параллелограмма:

1. Формула сторон параллелограмма через диагонали и угол между ними:

2. Формула сторон параллелограмма через диагонали и другую сторону:

a =	√ 2 d 1 2 + 2 d 2 2 – 4 b 2
2

b =	√ 2 d 1 2 + 2 d 2 2 – 4 a 2
2

3. Формула сторон параллелограмма через высоту и синус угла:

4. Формула сторон параллелограмма через площадь и высоту:

Диагонали параллелограмма

Формулы определения длины диагонали параллелограмма:

d ₁ = √ a 2 + b 2 – 2 ab·cosβ

d ₂ = √ a 2 + b 2 + 2 ab·cosβ

d ₁ = √ a 2 + b 2 + 2 ab·cosα

d ₂ = √ a 2 + b 2 – 2 ab·cosα

d ₁ = √ 2 a 2 + 2 b 2 – d ₂ 2

d ₂ = √ 2 a 2 + 2 b 2 – d ₁ 2

4. Формула диагонали параллелограмма через площадь, известную диагональ и угол между диагоналями:

d 1 =	2S	=	2S
d 2· sinγ	d 2· sinδ

d 2 =	2S	=	2S
d 1· sinγ	d 1· sinδ

Периметр параллелограмма

Формулы определения длины периметра параллелограмма:

P = 2 a + 2 b = 2( a + b )

P = 2 a + √ 2 d ₁ 2 + 2 d ₂ 2 – 4 a 2

P = 2 b + √ 2 d ₁ 2 + 2 d ₂ 2 – 4 b 2

3. Формула периметра параллелограмма через одну сторону, высоту и синус угла:

Площадь параллелограмма

Формулы определения площади параллелограмма:

3. Формула площади параллелограмма через две диагонали и синус угла между ними:

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Параллелограмм – четырехугольник с попарно параллельными противоположными сторонами.

Противолежащие стороны параллелограмма имеют одинаковую длину. Периметр параллелограмма находят как удвоенную сумму двух его сторон:

Формулы для вычисления длины периметра параллелограмма:

1. Формула периметра параллелограмма через стороны параллелограмма:

P = 2a + 2b = 2(a + b);

2. Формула периметра параллелограмма через 1-ну сторону и 2-е диагонали:

3. Формула периметра параллелограмма через 1-ну сторону, высоту и sin угла:

Свойства параллелограмма:

1. Противоположные стороны равны и параллельны

2. Противоположные углы равны

3. Точка пересечения диагоналей, делит их пополам

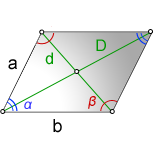
1. Длина диагонали параллелограмма через стороны, известную диагональ и угол.

a , b – стороны параллелограмма

D – большая диагональ

d – меньшая диагональ

α , β – углы параллелограмма

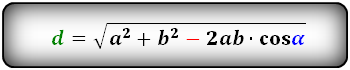
Формулы диагонали через стороны и углы параллелограмма (по теореме косинусов), ( D , d ):

Формулы диагонали через стороны и известную диагональ (по формуле- сумма квадратов диагоналей), ( D , d ):

2. Длина диагонали параллелограмма через площадь, известную диагональ и угол.

D – большая диагональ

d – меньшая диагональ

α , β – углы между диагоналями

S – площадь параллелограмма

Формулы диагонали через площадь, известную диагональ и угол между диагоналями, ( D , d ):

Источник