Содержание:
- Формула
- Примеры вычисления периметра равнобедренного треугольника
Формула
Чтобы найти периметр равнобедренного треугольника
$ABC$, нужно к длине его основание прибавить
удвоенную длину боковой стороны.
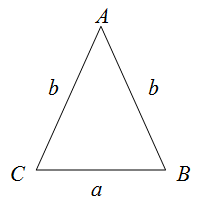
Периметр равнобедренного треугольника – это сумма длин его сторон. У равнобедренного треугольника боковые стороны равны.
Поэтому если $a$ – длина основания равнобедренного треугольника, а
$b$ – длина боковых сторон, то периметр равен
$$P_{Delta A B C}=a+b+b=a+2 b$$
Примеры вычисления периметра равнобедренного треугольника
Пример
Задание. В равнобедренном треугольнике
$ABC$ основание равно
7 м, а длины боковых сторон – 4 м. Найти его периметр.
Решение. Воспользуемся формулой для нахождения периметра равнобедренного треугольника
$$P_{Delta A B C}=a+2b$$
Тогда искомый периметр равен:
$P_{Delta A B C}=7+2 cdot 4=7+8=15$ (м)
Ответ. $P_{Delta A B C}=15$ (м)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти периметр равнобедренного треугольника
$ABC$, если его основание равно $a=8$ см и каждая из боковых сторон
$b$ составляют
75% от основания.
Решение. Найдем длину боковой стороны, для этого найдем 75% от длины основания:
$b=8 cdot 0,75=6$ (см)
Для вычисления периметра равнобедренного треугольника воспользуемся формулой:
$$P_{Delta A B C}=a + 2b$$
Тогда периметр $ABC$ равен:
$P_{Delta A B C}=8+2 cdot 6=8+12=20$ (см)
Ответ. $P_{Delta A B C}=20$ (см)
Читать дальше: как найти периметр равностороннего треугольника.
Чтобы найти периметр равнобедренного треугольника, нужно знать всего две его стороны — основание и боковую сторону.
В общем случае формула для нахождения периметра треугольника выглядит так:
![]()
где a, b и c — длины сторон треугольника.

Поскольку у равнобедренного треугольника
две стороны равны (боковые),
формулу можно упростить:
![]()
Таким образом, периметр равнобедренного треугольника равен сумме длин основания и удвоенной боковой стороны:
![]()

Соответственно, периметр равнобедренного треугольника ABC можно найти по формуле:
![]()
(здесь AC — основание, AB — боковая сторона).
Примеры.
1) Найти периметр равнобедренного треугольника, если его основание равно 4 см, а боковая сторона — 9 см.
Решение:
Здесь а=4 см, b=9 см. По формуле Р=а+2b имеем: P=4+2∙9=22 (cм).
2) Периметр равнобедренного треугольника равен 170 см, а его основание — 60 см. Найти боковую сторону треугольника.
Решение:
Здесь а=60 см, Р=170 см. По формуле Р=а+2b, 2b=Р-а, b=(Р-а):2, b=(170-60):2=55 (см).
Задача нахождения периметра равностороннего треугольника решается еще проще. Её мы рассмотрим в следующий раз.
Выбирайте формулу в зависимости от известных величин.
1. Как найти периметр треугольника, зная три стороны
Просто посчитайте сумму всех сторон.
- P — искомый периметр;
- a, b, c — стороны треугольника.
2. Как найти периметр треугольника, зная его площадь и радиус вписанной окружности
Умножьте площадь треугольника на 2.
Разделите результат на радиус вписанной окружности.
- P — искомый периметр;
- S — площадь треугольника;
- r — радиус вписанной окружности.
3. Как вычислить периметр треугольника, зная две стороны и угол между ними
Сначала найдите неизвестную сторону треугольника с помощью теоремы косинусов:
- Умножьте одну сторону на вторую, на косинус угла между ними и на 2.
- Посчитайте сумму квадратов известных сторон и отнимите от неё число, полученное в предыдущем действии.
- Найдите корень из результата.
Теперь прибавьте к найденной стороне две ранее известные стороны.
- P — искомый периметр;
- b, c — известные стороны треугольника;
- ɑ — угол между известными сторонами;
- a — неизвестная сторона треугольника.
4. Как найти периметр равностороннего треугольника, зная одну сторону
Умножьте сторону на 3.
- P — искомый периметр;
- a — любая сторона треугольника (напомним, в равностороннем треугольнике все стороны равны).
5. Как вычислить периметр равнобедренного треугольника, зная боковую сторону и основание
Умножьте боковую сторону на 2.
Прибавьте к результату основание.
- P — искомый периметр;
- a — боковая сторона треугольника (в равнобедренном треугольнике боковые стороны равны);
- b — основание треугольника (это сторона, которая отличается длиной от остальных).
6. Как найти периметр равнобедренного треугольника, зная боковую сторону и высоту
Найдите квадраты боковой стороны и высоты.
Отнимите от первого числа второе.
Найдите корень из результата и умножьте его на 2.
Прибавьте к полученному числу две боковые стороны.
- P — искомый периметр;
- a — боковая сторона треугольника;
- h — высота (перпендикуляр, опущенный на основание треугольника со стороны противоположной вершины; в равнобедренном треугольнике высота делит основание пополам).
7. Как вычислить периметр прямоугольного треугольника, зная катеты
Найдите квадраты катетов и посчитайте их сумму.
Извлеките корень из полученного числа.
Прибавьте к результату оба катета.
- P — искомый периметр;
- a, b — катеты треугольника (стороны, которые образуют прямой угол).
8. Как найти периметр прямоугольного треугольника, зная катет и гипотенузу
Посчитайте квадраты гипотенузы и катета.
Отнимите от первого числа второе.
Найдите корень из результата.
Прибавьте катет и гипотенузу.
- P — искомый периметр;
- a — любой катет прямоугольника;
- c — гипотенуза (сторона, которая лежит напротив прямого угла).
Периметр равнобедренного треугольника


4.5
Средняя оценка: 4.5
Всего получено оценок: 135.
4.5
Средняя оценка: 4.5
Всего получено оценок: 135.
Периметр – это сумма длин всех сторон фигуры. Эта характеристика, наравне с площадью, одинаково востребована для всех фигур. Формула периметра равнобедренного треугольника логично вытекает из его свойств, но формула не столь сложна, как получение и закрепление практических навыков.

Опыт работы учителем математики – более 33 лет.
Формула вычисления периметра
Боковые стороны равнобедренного треугольника равны между собой. Это вытекает из определения и хорошо видно даже из названия фигуры. Именно из этого свойства и вытекает формула периметра:
P=2a+b, где b – это основание треугольника, a – значение боковой стороны.
Из формулы видно, что для нахождения периметра достаточно знать величину основания и одной из боковых сторон. Рассмотрим несколько задач на нахождение периметра равнобедренного треугольника. Задачи будем решать по мере возрастания сложности, это позволит лучше понять способ размышления, которому нужно следовать для нахождения периметра.
Задача 1
- В равнобедренном треугольнике основание равно 6, а высота, проведенная к этому основанию, равна 4. Необходимо найти периметр фигуры.
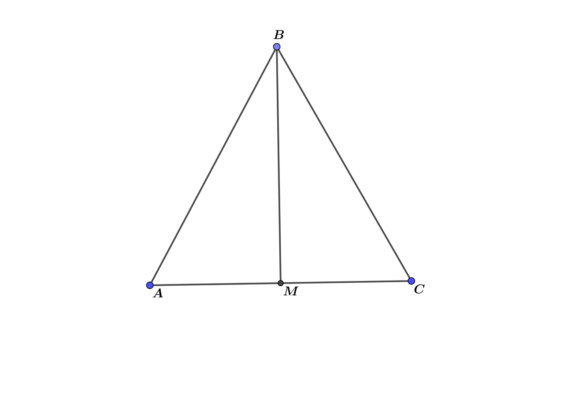
Высота равнобедренного треугольника, проведенная к основанию, является также медианой и биссектрисой. Это свойство очень часто используется при решении задач, связанных с равнобедренными треугольниками.
Треугольник АВС высотой ВM делится на два прямоугольных треугольника: АВM и ВСM. В треугольнике АВM катет ВM известен, катет АM равен половине основания треугольника АВС, так как ВM является медианой, биссектрисой и высотой. По теореме Пифагора найдем значение гипотенузы АВ.
$$АВ^2=AM^2+BM^2$$
$$AB=sqrt{AM^2+BM^2}=sqrt{3^2+4^2}=sqrt{9+16}=sqrt{25}=5$$
Найдем периметр: P=AC+AB*2=6+5*2=16
Задача 2
- В равнобедренном треугольнике высота, проведенная к основанию, равна 10, а острый угол при основании 30 градусам. нужно найти периметр треугольника.
Эта задача осложнена отсутствием сведений о сторонах треугольника, но, зная значение высоты и угла, в прямоугольном треугольнике ABH можно найти катет AH, а после решение пойдет по тому же сценарию, что и в задаче 1.
Найдем AH через значение синуса:
$$sin (ABH)={BHover AB}={1over2}$$ – синус 30 градусов является табличным значением.
Выразим нужную сторону:
$$AB={{BHover {1over 2}}} =BH*2=10*2=20$$
Через котангенс найдем значение AH:
$$ctg(BAH)={AHover BH}={1oversqrt{3}}$$
$$AH={BHoversqrt{3}}=10*sqrt{3}=17,32$$ – получившееся значение округлим до сотых.
Найдем основание:
AC=AH*2=17,32*2=34,64
Теперь, когда все требуемые значения найдены, определим периметр:
P=AC+2*AB=34,64+2*20=74,64
Задача 3
- В равнобедренном треугольнике ABC известна площадь, которая равна $$16oversqrt{3}$$ и острый угол при основании 30 градусов. Найти периметр треугольника.
Значения в условии часто приводятся в виде произведения корня на число. Это делается, чтобы максимально оградить последующее решение от погрешностей. Округлять результат лучше в конце вычислений
При такой постановке задачи может показаться, что решений нет, ведь сложно выразить одну из сторон или высоту из имеющихся данных. Попробуем решить по-другому.
Обозначим высоту и половину основания латинскими буквами: BH=h и AH=a
Тогда основание будет равно: AC=AH+HC=AH*2=2a
Площадь: $$S={1over 2}*AC*BH={1over 2}*2a*h=ah$$
С другой стороны, значение h можно выразить из треугольника ABH через тангенс острого угла. Почему именно тангенс? Потому что в треугольнике ABH мы уже обозначили два катета a и h. Нужно выразить одно через другое. Два катета вместе связывают тангенс и котангенс. Традиционно к котангенсу и косинусу обращаются, только если не подходит тангенс или синус. Это не правило, можно решать так, как удобно, просто так принято.
$$tg(BAH)={hover{a}}={1oversqrt{3}}$$
$$h={aoversqrt{3}}$$
Подставим полученное значение в формулу площади.
$$S=a*h=a*{aoversqrt{3}}={(a^2)oversqrt{3}}$$
Выразим a:
$$a=sqrt{S*sqrt{3}}=sqrt{16*sqrt{3}oversqrt{3}}=sqrt{16}=4$$
Подставим значение a в формулу площади и определим значение высоты:
$$S=a*h={16oversqrt{3}}$$
$$h={Sover{a}}={{16oversqrt{3}}over{4}}={4oversqrt{3}}=2,31$$– полученное значение округлим до сотых.
Через теорему Пифагора найдем боковую сторону треугольника:
$$AB^2=AH^2+BH^2$$
$$AB=sqrt{AH^2+BH^2}=sqrt{4^2+2,31^2}=4,62$$
Подставим значения в формулу периметра:
P=AB*2+AH*2=4,62*2+4*2=17,24

Что мы узнали?
Мы разобрались подробно во всех тонкостях нахождения периметра равнобедренного треугольника. Решили три задачи разного уровня сложности, показав на примере, как решаются типовые задачи на решение равнобедренного треугольника.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-

Яна Яночка
5/5
-

Наталия Левина
5/5
Оценка статьи
4.5
Средняя оценка: 4.5
Всего получено оценок: 135.
А какая ваша оценка?
Основные определения
Наверное, каждый из нас сталкивался с треугольником. Это могло быть в школе, вузах, колледжах, на работе, во время помощи детям. Треугольник – это одна из самых простых геометрических фигур, но в то же время она выполняет очень важную роль. Множество свойств хранит треугольник. Но сегодня не будем вдаваться в подробности, а поговорим про периметр и порешаем задачи по нахождению его.
Если мы отметим на плоскости 3 точки и проведём к ним линии, то как раз получим треугольник.
Понятия
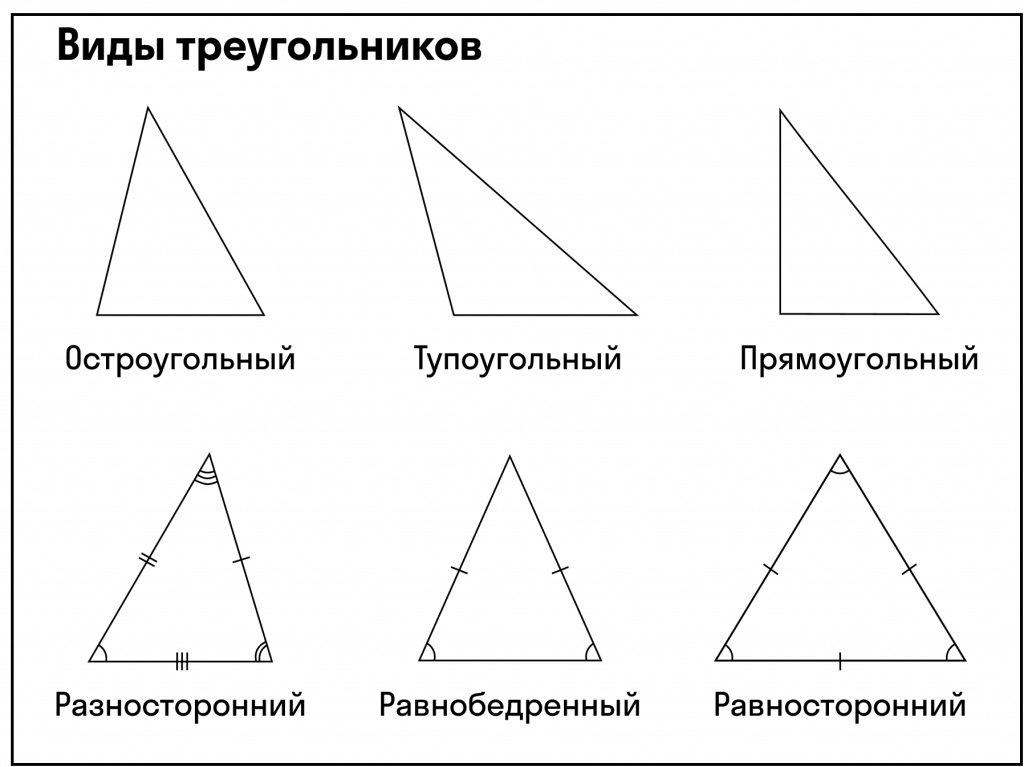
Треугольник – это геометрическая фигура, состоящая из трёх точек, которые соединены отрезками – сторонами. В зависимости от отношений между сторонами фигуры, то они бывают равносторонними, разносторонними и равнобедренными (р/б – равнобедренный, р/с – равносторонний).
Вершины треугольника – это точки, где соединяются 2 стороны фигуры.
Р/б треугольник – это треугольник у которого две стороны равны, но не равны третьей.
Р/с треугольник – это треугольник, у которого все стороны равны между собой.
Разносторонний треугольник – это треугольник, у которого все стороны не равны между собой.
Прямоугольный треугольник — это треугольник, у у которого один угол равен 90о. Самая длинная сторона называется гипотенузой, а две другие катетами.
Формула нахождения периметра
Из определения следует, что периметр геометрической фигуры – это сумма длин всех сторон, и треугольник не стал исключением. Общая формула имеет вид: Р = а + b + с. Периметр будет обозначаться Р. а, b и с — стороны треугольника. Решим задачу №1.
Задача 1
Пусть нам дан треугольник со сторонами 13 см, 15 см, 12 см. Нужно найти периметр данного треугольника.
Решение: [P=13+15+12=40] см.
Ответ: 40 см.
Периметр разностороннего треугольника
В прошлой задаче мы как раз нашли периметр разностороннего треугольника. Решим похожую задачу №2
Задача 2
Дан треугольник со сторонами 25 дм, 30 дм, 15 дм. Найдите периметр треугольника. Ответ выразите в метрах.
Решение:
P = 30 + 25 + 15 = 70 дм
70 : 10 = 7 м
Ответ: 7 м.
Периметр равнобедренного треугольника
Так как в р/б треугольнике 2 стороны равны (боковые), то формулу нахождения можно представить как: P = 2a + b. Решим 2 задачи.
Задачи 3 — 4
Дан равнобедренный треугольник АВС с биссектрисой, проведённой к основанию и равной 4 см, а также с боковой
стороной, равной 5 см. Найдите периметр данного треугольника.
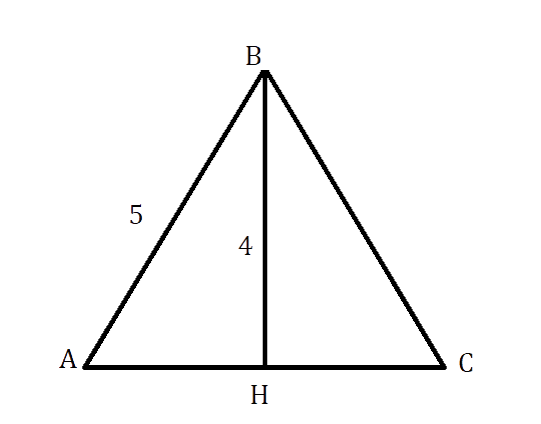
Решение:
Так как ВН – биссектриса р/б треугольника АВС, то она является как высотой, так и медианой. Следовательно, ΔАВН прямоугольный и АН = НС.
В ΔАВН по теореме Пифагора [A H^{2}=A B^{2}-B H^{2}=25-16=9]см
АН = НС = √9 = 3 см
АС = АН + НС = 3 + 3 = 6 см
Р = 6 + 2*5 = 16 см
Ответ: 16 см.
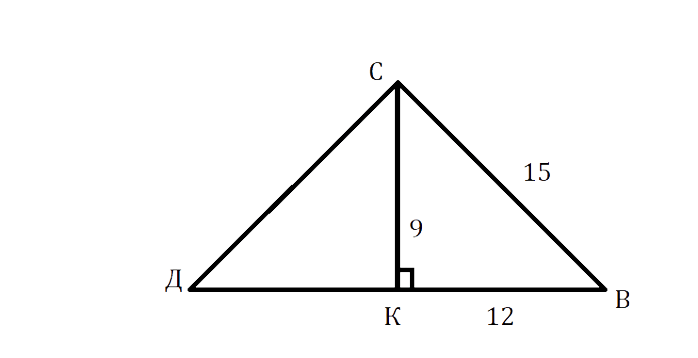
В треугольнике ДСВ ДС = СВ = 15 см, высота СК = 9 см. Найдите периметр этого треугольника.
Решение:
В ΔСКД по теореме Пифагора:
[text { ДК² }=text { ДС }^{2}-mathrm{CK}^{2}=225-81=144]см
ДК = √144 = 12 см.
Так как СК — высота в р/б треугольнике, проведённая к основанию, то она является медианой, следовательно, ДВ = ДК + КВ = 12 + 12 = 24 см.
Р = ДС + СВ + ДВ = 15 + 15 + 24 = 54 см.
Ответ: 54 см.
Нет времени решать самому?
Наши эксперты помогут!
Периметр равностороннего треугольника
А это один из самых “хороших” треугольников, его ещё называют правильным, так как все стороны и углы равны между собой. Формула нахождения периметра будет иметь вид: P = 3a.
Задачи 5 — 6
Дан равносторонний треугольник со стороной а = 13. Найдите периметр этого треугольника.
Решение:
Р = 3а = 3 * 13 = 39
Ответ: 39.
В равностороннем треугольнике АВС есть стороны: АВ = АС = СВ = 15 см, Найдите периметр данного треугольника.
Решение:
Р = 3АВ = 15 * 3 = 45 см.
Ответ: 45 см.
Периметр прямоугольного треугольника
Вычисляем по стандартной формуле: Р = а + в + с. Но у такого вида треугольников есть огромное преимущество – применение теоремы Пифагора.
Задачи 7 — 8
Дан прямоугольный треугольник с катетами а = 6 и в = 8. Найдите периметр.
Решение:
По теореме Пифагора: [c^{2}=в^{2}+a^{2}=64+36=100]
с = √100 = 10
Р = а + в + с = 6 + 8 + 10 = 24
Ответ: 24.
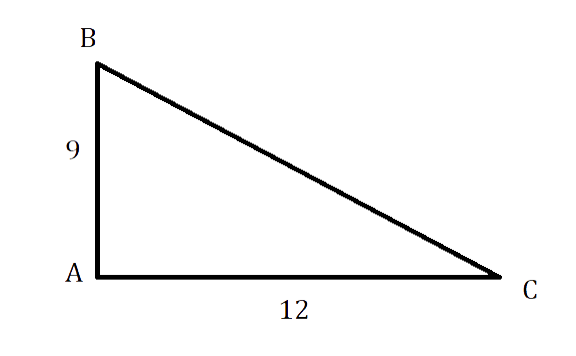
В прямоугольном треугольнике АВС, [angle mathrm{A}=90^{circ}, mathrm{AB}=9 mathrm{~см}, mathrm{AC} = 12см]. Надо найти периметр и площадь АВС.
Решение
По теореме Пифагора в ΔАВС:
[mathrm{CB}^{2}=mathrm{AC}^{2}+A mathrm{C}^{2}=144+81=225 mathrm{~см}]
СВ = √225 = 15 см
S = (АС * АВ) : 2 = (9 * 12) : 2 = 54 см
P = 15 + 9 + 12 = 36 см
Ответ: 36 см; 54 см.