Расчёт периметра равнобедренного треугольника по основанию и высоте
Калькулятор рассчитывает периметр равнобедренного треугольника по основанию и высоте.
Введите основание
Введите высоту
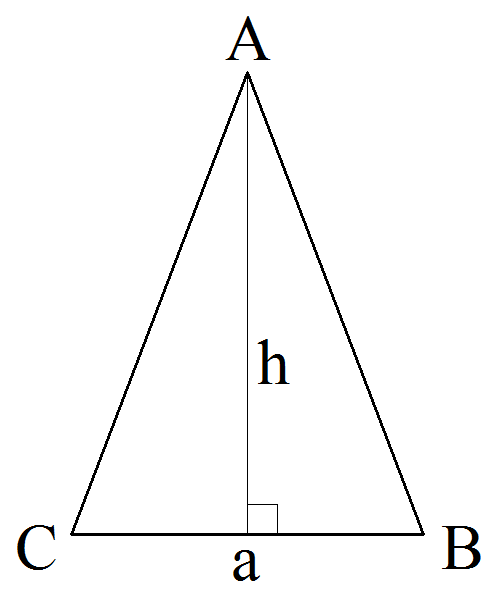
Периметром треугольника называется сумма всех длин его сторон.
Определение равнобедренного треугольника
Треугольник называется равнобедренным если две его стороны равны. Равные стороны называются боковыми, а третья основанием.
Определение высоты треугольника
Высотой треугольника называется перпендикуляляр опущенные с вершины треугольника к прямой содержащей противоположную сторону.
Формула периметра равнобедренного треугольника по основанию и высоте
Подставим в формулу периметра
Получится
Где a – основание, h – высота треугольника
Разберём пример
Дан равнобедренный треугольник с основанием 6 и высотой 4
По теореме Пифагора найдём боковую сторону
Подставим в формулу периметра
Похожие калькуляторы
Выбирайте формулу в зависимости от известных величин.
1. Как найти периметр треугольника, зная три стороны
Просто посчитайте сумму всех сторон.
- P — искомый периметр;
- a, b, c — стороны треугольника.
2. Как найти периметр треугольника, зная его площадь и радиус вписанной окружности
Умножьте площадь треугольника на 2.
Разделите результат на радиус вписанной окружности.
- P — искомый периметр;
- S — площадь треугольника;
- r — радиус вписанной окружности.
3. Как вычислить периметр треугольника, зная две стороны и угол между ними
Сначала найдите неизвестную сторону треугольника с помощью теоремы косинусов:
- Умножьте одну сторону на вторую, на косинус угла между ними и на 2.
- Посчитайте сумму квадратов известных сторон и отнимите от неё число, полученное в предыдущем действии.
- Найдите корень из результата.
Теперь прибавьте к найденной стороне две ранее известные стороны.
- P — искомый периметр;
- b, c — известные стороны треугольника;
- ɑ — угол между известными сторонами;
- a — неизвестная сторона треугольника.
4. Как найти периметр равностороннего треугольника, зная одну сторону
Умножьте сторону на 3.
- P — искомый периметр;
- a — любая сторона треугольника (напомним, в равностороннем треугольнике все стороны равны).
5. Как вычислить периметр равнобедренного треугольника, зная боковую сторону и основание
Умножьте боковую сторону на 2.
Прибавьте к результату основание.
- P — искомый периметр;
- a — боковая сторона треугольника (в равнобедренном треугольнике боковые стороны равны);
- b — основание треугольника (это сторона, которая отличается длиной от остальных).
6. Как найти периметр равнобедренного треугольника, зная боковую сторону и высоту
Найдите квадраты боковой стороны и высоты.
Отнимите от первого числа второе.
Найдите корень из результата и умножьте его на 2.
Прибавьте к полученному числу две боковые стороны.
- P — искомый периметр;
- a — боковая сторона треугольника;
- h — высота (перпендикуляр, опущенный на основание треугольника со стороны противоположной вершины; в равнобедренном треугольнике высота делит основание пополам).
7. Как вычислить периметр прямоугольного треугольника, зная катеты
Найдите квадраты катетов и посчитайте их сумму.
Извлеките корень из полученного числа.
Прибавьте к результату оба катета.
- P — искомый периметр;
- a, b — катеты треугольника (стороны, которые образуют прямой угол).
8. Как найти периметр прямоугольного треугольника, зная катет и гипотенузу
Посчитайте квадраты гипотенузы и катета.
Отнимите от первого числа второе.
Найдите корень из результата.
Прибавьте катет и гипотенузу.
- P — искомый периметр;
- a — любой катет прямоугольника;
- c — гипотенуза (сторона, которая лежит напротив прямого угла).
Расчёт периметра равнобедренного треугольника по основанию и высоте
Калькулятор рассчитывает периметр равнобедренного треугольника по основанию и высоте.

Периметром треугольника называется сумма всех длин его сторон.
Определение равнобедренного треугольника
Треугольник называется равнобедренным если две его стороны равны. Равные стороны называются боковыми, а третья основанием.
Определение высоты треугольника
Высотой треугольника называется перпендикуляляр опущенные с вершины треугольника к прямой содержащей противоположную сторону.
Как найти периметр треугольника

О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение
Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской буквой P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах и ходе решении.
Важно, чтобы все параметры были переданы в одной единице длины, иначе мы не сможем подсчитать результат. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
В чем измеряется периметр:
Как узнать периметр треугольника
Рассмотрим какие существуют формулы, и при каких известных исходных данных их можно применять.
Если известны три стороны, то периметр треугольника равен их сумме. Этот способ проходят во втором классе.
P = a + b + c, где a, b, c — длина стороны.
Если известна площадь и радиус вписанной окружности:
P = 2 * S : r, где S — площадь, r — радиус вписанной окружности.
Если известны две стороны и угол между ними, вычислить периметр треугольника можно так:
P = √ b 2 + с 2 – 2 * b * с * cosα + (b + с), где b, с — известные стороны, α — угол между известными сторонами.
Если известна одна сторона в равностороннем треугольнике:
P = 3 * a, где a — длина стороны.
Все стороны в равносторонней фигуре равны.
Если известна боковая сторона и основание в равнобедренном треугольнике:
P = 2 * a + b, где a — боковая сторона, b — основание.
Боковые стороны в равнобедренной фигуре равны.
Если известна боковая сторона и высота в равнобедренном треугольнике:
P = 2 * (√ a 2 + h 2 ) + 2 * a, где a — боковая сторона, h — высота.
Высотой принято называть отрезок, который вышел из вершины и опустился на основание. В равнобедренной фигуре высота делит основание пополам.
Если известны катеты в прямоугольном треугольнике:
P = √ a 2 + b 2 + (a + b), где a, b — катеты.
Катет — одна из двух сторон, которые образуют прямой угол.
Если известны катет и гипотенуза в прямоугольном треугольнике:
P = √ c 2 – a 2 + (a + c), где a — любой катет, c — гипотенуза.
Гипотенуза — сторона, которая лежит напротив прямого угла.
Скачать онлайн таблицу
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
Формула периметра равнобедренного треугольника
Периметр равнобедренного треугольника ABC , длины сторон которого соответственно равны: боковые стороны AB = BC = a , основание AC = b вычисляется по формуле:
Периметр равнобедренного треугольника вычисляется по формуле:
( P_ <Delta ABC>= a + b + c = 2 cdot a + b)
где a,b,c – стороны равнобедренного треугольника.
Основные понятия, справедливые для треугольников
- Сумма углов треугольника равна 180°.
- Высота – это отрезок перпендикуляра, опущенного из вершины на противоположную сторону.
- Центр описанной окружности лежит на пересечении медиатрис.
- Медиатриса – это перпендикулярна прямая, проходящая через середину стороны.
- Центр вписанной окружности лежит на пересечении биссектрис углов.
- Биссектриса угла делит угол на две равные части.
- Медиана – это отрезок, соединяющий вершину с серединой противоположной стороны.
- Медианы пересекаются в центре тяжести, который делит каждую медиану в отношение 2:1.
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
О сайте
На нашем сайте вы найдете множество полезных калькуляторов, конвертеров, таблиц, а также справочных материалов по основным дисциплинам.
Самый простой способ сделать расчеты в сети — это использовать подходящие онлайн инструменты. Воспользуйтесь поиском, чтобы найти подходящий инструмент на нашем сайте.
calcsbox.com
На сайте используется технология LaTeX.
Поэтому для корректного отображения формул и выражений
пожалуйста дождитесь полной загрузки страницы.
© 2022 Все калькуляторы online
Копирование материалов запрещено
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/perimetr-treugolnika
http://calcsbox.com/post/formula-perimetra-ravnobedrennogo-treugolnika.html
[/spoiler]
Так как изначально периметр для любой фигуры – это сумма длин всех ее сторон, то периметр треугольника найти проще всего, зная все три стороны: P=a+b+c. Для равнобедренного треугольника формула периметра будет выглядеть несколько иначе в силу того, что две из сторон у него конгруэнтны, то есть равны по значению: P=2a+b. С равносторонним треугольником все еще незатейливей – у него все три стороны одинаковые, поэтому периметр будет равен утроенной стороне: P=3a.
Для треугольников, обладающих особыми свойствами, как например, вышеупомянутые равнобедренный и равносторонний треугольники, могут быть выведены и другие формулы. Например, периметр равнобедренного треугольника можно найти и через высоту. Высота в данном случае делит основание пополам, исходя из чего можно найти неизвестную сторону по теореме Пифагора из получившихся прямоугольных треугольников. Если дана боковая сторона, то половина основания будет равна  , а само основание, соответственно,
, а само основание, соответственно,  . Подставив его в формулу для нахождения периметра равнобедренного треугольника, получим
. Подставив его в формулу для нахождения периметра равнобедренного треугольника, получим  . Если дано основание, то по той же теореме Пифагора находим боковую сторону
. Если дано основание, то по той же теореме Пифагора находим боковую сторону  . Формула периметра равнобедренного треугольника через основание и высоту тогда принимает вид
. Формула периметра равнобедренного треугольника через основание и высоту тогда принимает вид  .
.
Найти периметр равностороннего треугольника становится возможным, уже зная одну лишь высоту. Используя теорему Пифагора, выражаем сторону треугольника через высоту  . Подставляем в формулу периметра равностороннего треугольника и получаем
. Подставляем в формулу периметра равностороннего треугольника и получаем 
Периметр прямоугольного треугольника можно найти, зная две стороны из трех. Если известны два катета a и b, то гипотенуза c по теореме Пифагора равна  , и периметр получается
, и периметр получается  . Если дана гипотенуза и один из катетов, формула периметра прямоугольного треугольника принимает уже другой вид:
. Если дана гипотенуза и один из катетов, формула периметра прямоугольного треугольника принимает уже другой вид: 
Треугольник – это геометрическая фигура, состоящая из трех точек (вершины треугольника), не лежащих на одной прямой, соедененных тремя отрезками (стороны треугольника).
Формула периметра треугольника: 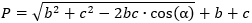
где b,c – стороны треугольника, α° – угол между ними.
Решение:
P = √b2 + с2 – 2bc·cos(α°) + b + c
= √8.22 + 62 – 2·8.2·6·cos(90°) + 8.2 + 6
= √67.24 + 36 – 0 + 14.2
= √103.24 + 14.2
= 10.161 + 14.2
=
24.361
Ответ: Периметр треугольника со сторонами b = 8.2, c = 6 и углом между ними α° = 90 равен 24.361
