Перейти к содержанию
Периметр правильного пятиугольника
На чтение 1 мин
Пятиугольник – это многоугольник, который имеет пять углов.
Правильный пятиугольник – это выпуклый пятиугольник, у которого все углы и все стороны равны.
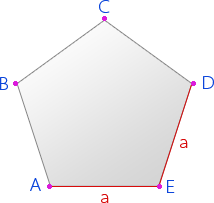 a – сторона правильного пятиугольника
a – сторона правильного пятиугольника
A, B, C, D, E – вершины пятиугольника
Периметр правильного пятиугольника (P) равен сумме 5-ти его сторон (a) или:
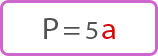
Вам также может понравиться
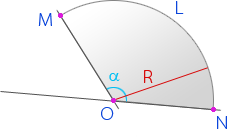
Дуга – это часть окружности, отсекаемая хордой.
0139
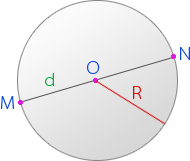
Окружность – геометрическое место точек, равноудаленных
0122

Окружность – геометрическое место точек, равноудаленных
0121
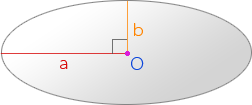
Эллипс – это множество точек плоскости, для которых
02.9к.
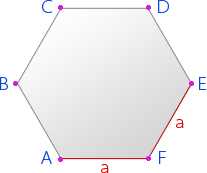
Многоугольник – это геометрическая фигура, которая
0137
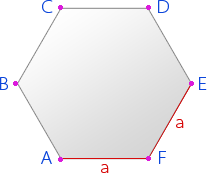
Шестиугольник – это многоугольник, который имеет шесть углов.
0422
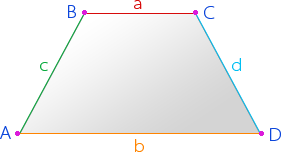
Трапеция – это четырехугольник, у которого параллельна
087
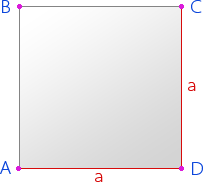
Квадрат – это параллелограмм, у которого все углы и
089
Периметр пятиугольника
Пятиугольник – это многоугольник, который имеет пять углов.
Правильный пятиугольник – это выпуклый пятиугольник, у которого все углы и все стороны равны.
a – сторона правильного пятиугольника
A , B , C , D , E – вершины пятиугольника
Периметр правильного пятиугольника (P) равен сумме 5-ти его сторон ( a ) или:
Периметр пятиугольника (пентагона).
Пятиугольник (пентагон) — геометрическая фигура, ограниченная пятью отрезками. произвольный пятиугольник может иметь разные стороны, разные углы и строиться с самопересечениями, однако такая форма многоугольника крайне редко встречается в реальности.
Формула расчёта периметра пятиугольника (пентагона) зная длину сторон: p = a × 5,
где a — длина стороны.
Формула расчёта периметра пятиугольника (пентагона) зная радиус вписанной окружности: a = 1,4131 × r,
где r — радиус вписанной окружности, дальше используем формулу расчёта периметра пятиугольника (пентагона).
Формула расчёта периметра пятиугольника (пентагона) зная радиус описанной окружности: a = 1,1756 × r,
где r — радиус описанной окружности, дальше используем формулу расчёта периметра пятиугольника (пентагона).
Как найти периметр фигуры

О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Определение периметра
Периметр — это сумма длин всех сторон многоугольника.
Какой буквой обозначается периметр? Заглавной латинской P. Под обозначением P удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.
В чем измеряется периметр? В тех же единицах измерения, что и длина — например, миллиметр, сантиметр, метр, фут, дюйм, локоть и др.
Если в условиях задачки длины сторон переданы в разных единицах длины, мы не сможем узнать периметр фигуры. Для правильного решения нужно перевести все данные в одну единицу измерения.
Формулы нахождения периметра
Как мы только что узнали, периметр — это сумма длин всех сторон многоугольника. А значит, чтобы его найти, нам надо знать длины этих сторон. Давайте посмотрим, как найти периметр, на примерах нескольких фигур.
Равносторонний многоугольник
У равностороннего треугольника все стороны равны. А значит, периметр равностороннего треугольника можно найти как произведение длины стороны на их количество, т. е. на 3.

P = 3 ⋅ a, где a — длина стороны.
Периметр любого другого равностороннего многоугольника можно найти тем же способом: умножив длину его стороны на их количество. Например, у квадрата и ромба все стороны равны, а значит, их периметр можно найти по формуле P = 4 ⋅ a, где a — длина стороны.
А формула для любого равностороннего n-угольника будет такая: P = n ⋅ a, где a — длина стороны, n — количество сторон.
Прямоугольник и параллелограмм
У прямоугольника и параллелограмма противоположные стороны равны, а значит, найти их периметр легко, зная две соседние стороны.
P = 2 ⋅ (a + b), где a — одна сторона, b — соседняя сторона.
Окружность
У окружности нет периметра, потому что это не многоугольник. Но у нее есть длина, которую можно найти, зная радиус. Длина окружности — это произведение пи на два радиуса или произведение пи на диаметр.
L = d ⋅ π = 2 ⋅ r ⋅ π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она приблизительно равна 3,14.
Можно выучить все формулы, а можно, запомнив определение о сумме всех сторон, каждый раз проявлять смекалку и вычислять самостоятельно. Давайте потренируемся, как определять периметр фигур!
Решение задач
Площадь прямоугольника равна 80 см 2 , длина составляет 10 см. Чему равен периметр фигуры?
- Для использования формулы P = 2 × (a + b), нам нужно найти ширину;
- Так как S = a × b, для поиска одной стороны необходимо разделить площадь на известную сторону: 80 : 10 = 8 см;
- Далее подставляем известные данные в формулу: (10 + 8) × 2 = 36 см;
Равнобедренный треугольник имеет периметр 40 см, длина его основания составляет 6 см. Какую длину будут иметь две другие стороны?
- Мы знаем, что периметр — это сумма длин всех сторон, а значит, если вычесть из данного периметра сторону основания — получим сумму двух оставшихся сторон: 40 − 6 = 34 см;
- Известно, что равнобедренный треугольник имеет две равные стороны;
- Далее делим получившуюся сумму на два: 34 : 2 = 17 см;
Ответ: две другие стороны равны по 17 см.
Радиус окружности равен периметру равностороннего пятиугольника со стороной 4 см. Найдите длину окружности.
- Периметр равностороннего пятиугольника равен 4 × 5 = 20 см, значит, радиус окружности равен 20 см;
- Длина окружности равна π × 2 × 20 = 40π см;
Еще больше практических заданий — на курсах по математике в онлайн-школе Skysmart!
[spoiler title=”источники:”]
http://codemg.ru/geometry/perimetr_pyatiugolnika.php
http://skysmart.ru/articles/mathematic/perimetr-figury
[/spoiler]
Как найти периметр пятиугольника
Нахождение периметра пятиугольника – задача, требующая обширных теоретических знаний, пространственного и логического мышления. Важно также и правильно оформить решение.

Вам понадобится
- – Тетрадь;
- – линейка;
- – карандаш;
- – ручка;
- – калькулятор.
Инструкция
Пятиугольник – это многоугольник с пятью углами. Пятиугольники бывают правильными и неправильными. Правильный пятиугольник — это выпуклый многоугольник, у которого все стороны и все углы равны между собой.
Неправильный пятиугольник – это многоугольник, стороны и углы которого не равны. В базовом курсе геометрии чаще рассматриваются правильные пятиугольники.
Периметр многоугольника – это сумма длин всех его сторон. Чтобы найти периметр пятиугольника, вычислите длину каждой стороны, а затем сложите их.
Если в задаче дано, что сторона правильного пятиугольника АВСDF равна 5 см, то периметр его будет равен:
P = 5АВ
P = 5*5 = 25
В данном случае вы просто умножаете длину стороны пятиугольника на количество сторон, т.к. все они равны между собой (Рис.1).
Если же в задании вам встретился неправильный пятиугольник, то вы должны сначала найти длину каждой его стороны, а потом сложить их.
К примеру, в задаче говорится, что ВО = 8, ОF = 4, ВС = 7, угол ВОА = 90, угол ОАМ = 45, ОМ = 3, АВ = DF, ВС = СD. Вначале рассмотрите треугольник АОВ: ВО = 8. Из условия следует, что АО = ОF = 4. Треугольник АОВ является прямоугольным. АО и ОF – катеты, АВ – гипотенуза. По теореме Пифагора, квадрат гипотенузы равен сумме квадратов катетов.
Следовательно, АВ ^2 = АО ^2 + ОF ^2.
АВ ^2 = 8^2 + 4^2
АВ ^2 = 64 + 16
АВ ^2 = 80
АВ = √80
АВ = 8,94
АВ = DF = 8,94.
Затем рассмотрите треугольник АОF. АО = ОF = 4, ОМ = 3. Угол АОВ = DОF = 90 (как накрест лежащие). Следовательно, АОМ = ВОD (как накрест лежащие), и значит АОМ + ВОD = 360 – АОВ + DОF = 180. АОМ = 90.
Отсюда следует, что треугольник АОF – прямоугольный.
Значит угол АМО = АОМ – ОАМ,
АМО = 90 – 45, АМО = 45.
Следовательно, треугольник АОF – равнобедренный. А в равнобедренных треугольниках напротив равных углов лежат равные стороны. Значит АМ = ОМ = 3.
Отсюда АF = 2АМ = 6.
Теперь вы можете вычислить периметр пятиугольника АВСDF.
Р = 8,94*2+7*2+6
Р = 37,88
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Содержание материала
- Формула
- Видео
- Периметр треугольника
- Что такое периметр?
- Площадь квадрата
- Перевод единиц измерения площади
- Нахождение периметра параллелограмма
- Нахождение периметра многоугольника
- Решение задач
Формула
Чтобы найти периметр треугольника $ABC$, необходимо сложить длины всех его сторон.
Напомним, что периметр треугольника — это сумма длин всех его сторон. То есть если задан произвольный треугольник $ABC$ и длины его сторон соответственно равны $AB=c$, $AC=b$, $BC=a$, то периметр треугольника вычисляется по формуле:
$$P_{Delta A B C}=a+b+c$$

Видео
Периметр треугольника
Треугольником следует называть геометрическую фигуру, имеющую три угла (как разного значения, так и одинакового) и состоящую из отрезков, образованных от точек пересечения лучей, образующих углы. Треугольник имеет три стороны и три угла. В нем могут быть из трех равны две стороны. Такой треугольник следует считать равнобедренным. Бывают такие фигуры, в которых равны все три стороны между собой. Принято такие треугольники называть равносторонними.
Что такое периметр треугольника? Его вычисление можно провести по аналогии с периметром четырехугольника. Равен периметр треугольника суммарной длине длин его сторон. Вычисление периметра треугольника, в котором две стороны равны – равнобедренного – упрощается умножением одной длины равных сторон на два. К полученному значению необходимо прибавить значение длины третьей стороны. Вычисление периметра треугольника с равными сторонами можно свести к простому вычислению произведения одной длины стороны треугольника на три.
Читать еще: Тест нарисовать дом дерево человека расшифровка пример. Методика исследования личности «Дом-дерево-человек» Дж

Что такое периметр?
Периметром называют суммарную длину всех сторон геометрической фигуры. Для его обозначения используется буква латинского алфавита «Р». Проще говоря, чтобы найти периметр, необходимо измерить длины всех сторон геометрической фигуры и сложить полученные значения. Длина вычисляется обычным измерительным прибором, таким как линейка, рулетка, сантиметровая лента и прочее.
Единицей измерения соответственно являются сантиметры, метры, миллиметры и другие меры длины. Длина стороны многоугольника вычисляется путем прикладывания измерительного прибора от одной вершины к другой. Начало шкалы деления прибора должно совпадать с одной из вершин. Второе числовое значение, на которое попадает другая вершина и является длиной стороны многоугольника. Таким же образом необходимо измерить все длины сторон фигуры и полученные значения сложить. Единицей измерения периметра является та же самая единица, которая используется для измерения стороны фигуры.
Площадь квадрата
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, на следующем рисунке представлен квадрат со стороной 3 см. Фраза «квадрат со стороной 3 см» означает, что все стороны равны 3 см

Площадь квадрата вычисляется таким же образом, как и площадь прямоугольника — длину умножают на ширину.
Вычислим площадь квадрата со стороной 3 см. Умножим длину 3 см на ширину 3 см
3 × 3 = 9
В данном случае требовалось узнать сколько квадратов со стороной 1 см содержится в исходном квадрате. В исходном квадрате содержится девять квадратов со стороной 1 см. Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз:

Умножив длину на ширину, мы получили выражение 3 × 3, а это есть произведение двух одинаковых множителей, каждый из которых равен 3. Иными словами выражение 3 × 3 представляет собой вторую степень числа 3. А значит процесс вычисления площади квадрата можно записать в виде степени 32.
Поэтому вторую степень числа называют квадратом числа. При вычислении второй степени числа a, человек тем самым находит площадь квадрата со стороной a. Операцию возведения числа во вторую степень по другому называют возведением в квадрат.
Перевод единиц измерения площади
Единицы измерения площади можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:
Пример 1. Выразить 1 квадратный метр в квадратных сантиметрах.
1 квадратный метр это квадрат со стороной 1 м. То есть все четыре стороны имеют длину, равную одному метру.

Но 1 м = 100 см. Тогда все четыре стороны тоже имеют длину, равную 100 см

Вычислим новую площадь этого квадрата. Умножим длину 100 см на ширину 100 см или возведём в квадрат число 100
S = 1002 = 10 000 см2
Получается, что на один квадратный метр приходится десять тысяч квадратных сантиметров.
1 м2 = 10 000 см2
Это позволяет в будущем умножить любое количество квадратных метров на 10 000 и получить площадь, выраженную в квадратных сантиметрах.
Чтобы перевести квадратные метры в квадратные сантиметры, нужно количество квадратных метров умножить на 10 000.
А чтобы перевести квадратные сантиметры в квадратные метры, нужно наоборот количество квадратных сантиметров разделить на 10 000.
Например, переведём 100 000 см2 в квадратные метры. Рассуждать в этом случае можно так: «если 10 000 см2 это один квадратный метр, то сколько раз 100 000 см2 будут содержать по 10 000 см2»
100 000 см2 : 10 000 см2 = 10 м2
Другие единицы измерения можно переводить таким же образом. Например, переведём 2 км2 в квадратные метры.
Один квадратный километр это квадрат со стороной 1 км. То есть все четыре стороны имеют длину, равную одному километру. Но 1 км = 1000 м. Значит, все четыре стороны квадрата также равны 1000 м. Найдём новую площадь квадрата, выраженную в квадратных метрах. Для этого умножим длину 1000 м на ширину 1000 м или возведём в квадрат число 1000
S = 10002 = 1 000 000 м2
Получается, что на один квадратный километр приходится один миллион квадратных метров:
1 км2 = 1 000 000 м2
Это позволяет в будущем умножить любое количество квадратных километров на 1 000 000 и получить площадь, выраженную в квадратных метрах.
Чтобы перевести квадратные километры в квадратные метры, нужно количество квадратных километров умножить на 1 000 000.
Итак, вернёмся к нашей задаче. Требовалось перевести 2 км2 в квадратные метры. Умножим 2 км2 на 1 000 000
2 км2 × 1 000 000 = 2 000 000 м2
А чтобы перевести квадратные метры в квадратные километры, нужно наоборот количество квадратных метров разделить на 1 000 000.
Например, переведём 3 500 000 м2 в квадратные километры. Рассуждать в этом случае можно так: «если 1 000 000 м2 это один квадратный километр, то сколько раз 3 500 000 м2 будут содержать по 1 000 000 м2»
3 500 000 м2 : 1 000 000 м2 = 3,5 км2
Пример 2. Выразить 7 м2 в квадратных сантиметрах.
Умножим 7 м2 на 10 000
7 м2 = 7 м2 × 10 000 = 70 000 см2
Пример 3. Выразить 5 м2 13 см2 в квадратных сантиметрах.
5 м2 13 см2 = 5 м2 × 10 000 + 13 см2 = 50 013 см2
Пример 4. Выразить 550 000 см2 в квадратных метрах.
Узнаем сколько раз 550 000 см2 содержит по 10 000 см2. Для этого разделим 550 000 см2 на 10 000 см2
550 000 см2 : 10 000 см2 = 55 м2
Пример 5. Выразить 7 км2 в квадратных метрах.
Умножим 7 км2 на 1 000 000
7 км2 × 1 000 000 = 7 000 000 м2
Пример 6. Выразить 8 500 000 м2 в квадратных километрах.
Узнаем сколько раз 8 500 000 м2 содержит по 1 000 000 м2. Для этого разделим 8 500 000 м2 на 1 000 000 м2
8 500 000 м2 × 1 000 000 м2 = 8,5 км2
Нахождение периметра параллелограмма
Определение
Параллелограмм – это такой четырехугольник, у которого противоположные стороны порно параллельны.
Характеристики:
- Противоположные стороны равны.
- Противоположные углы равны.
- Диагонали в точке пересечения делятся пополам.
- Как и в прямоугольнике, диагональ параллелограмма делит его на 2 треугольника.
- Два угла на одной стороне равны 180°

Периметр параллелограмма находится точно так же, как и периметр прямоугольника:
[P = a + a + b + b]
[P = 2(a + b)]
[P = 2a + 2b]
Нахождение периметра многоугольника
Определение
Многоугольник – это геометрическая фигура, которая со всех сторон ограничена ломанной линией.
Характеристики:
- Название многоугольника определяется количеством его вершин. Если у многоугольника количество вершин равно n, то он называется n-угольником.
- Многоугольником являются такие фигуры, как: квадрат, ромб, параллелограмм и т.д.
- Если углы с отрезками равны, то это правильный многоугольник.

Чтобы найти периметр n-угольника, нужно сложить всего длины его сторон:
[P = a1 + a2 + … an]
А для правильного n-угольника можно выделить еще одну формулу, потому как его стороны равны:
P = na
Здесь мы умножаем длину одной стороны на n.
Пример 1
Найдите периметр правильного многоугольника, если у него 5 вершин, а длина его одной стороны равна 7.
Решение:
Здесь воспользуемся этой формулой:
P = na
7 × 5 = 35 (см)
Ответ: периметр многоугольника равняется 35 см.
Решение задач
Площадь прямоугольника равна 80 см2, длина составляет 10 см. Чему равен периметр фигуры?
Как решаем:
- Для использования формулы P = 2 × (a + b), нам нужно найти ширину;
- Так как S = a × b, для поиска одной стороны необходимо разделить площадь на известную сторону: 80 : 10 = 8 см;
- Далее подставляем известные данные в формулу: (10 + 8) × 2 = 36 см;
Ответ: 36 см.
Равнобедренный треугольник имеет периметр 40 см, длина его основания составляет 6 см. Какую длину будут иметь две другие стороны?
Как решаем:
- Мы знаем, что периметр — это сумма длин всех сторон, а значит, если вычесть из данного периметра сторону основания — получим сумму двух оставшихся сторон: 40 − 6 = 34 см;
- Известно, что равнобедренный треугольник имеет две равные стороны;
- Далее делим получившуюся сумму на два: 34 : 2 = 17 см;
Ответ: две другие стороны равны по 17 см.
Радиус окружности равен периметру равностороннего пятиугольника со стороной 4 см. Найдите длину окружности.
Как решаем:
- Периметр равностороннего пятиугольника равен 4 × 5 = 20 см, значит, радиус окружности равен 20 см;
- Длина окружности равна π × 2 × 20 = 40π см;
Ответ: 40π см.
Еще больше практических заданий — на курсах по математике в онлайн-школе Skysmart!
Теги
Пятиугольник — это многоугольник с пятью углами. Если углы и стороны такого многоугольника равны, то он считается правильным и называется пентагон. Это оригинальная фигура, которую большинство людей встречает только в учебнике по геометрии.
Геометрия пятиугольника
Пятиугольник — геометрическая фигура, ограниченная пятью отрезками. Произвольный пятиугольник может иметь разные стороны, разные углы и строиться с самопересечениями, однако такая форма многоугольника крайне редко встречается в реальности. Самой распространенной формой пятиугольника считается пентагон — выпуклый многоугольник с равными сторонами и углами. Геометрическая фигура считается выпуклой, если все точки фигуры лежат с одной стороны от любой прямой, проведенной через две соседние вершины.
В отличие от треугольника, изучение которого не прерывалось на протяжении веков, все тайны пятиугольника были открыты еще в Древней Греции. В третьем веке до нашей эры Евклид описал метод построения пентагона с помощью линейки и циркуля. Пифагор изучал диагонали пентагона, которые образуют отдельную фигуру — пентаграмму, идеальную по мнению античного ученого, так как отношение сторон пентаграммы и пентагона демонстрирует золотое сечение.
Пятиугольник в реальности
В человеческой повседневности пятиугольник встречается редко, так как пентагоном невозможно замостить плоскость без пробелов, а пентагональные призмы неудобно хранить. Форма пентагона используется обычно в архитектуре, и наиболее известным объектом, имеющим форму правильного пятиугольника, является здание министерства обороны США.
Додекаэдр – трехмерное воплощение пятиугольника, является правильным многогранником, каждая сторона которого — пентагон. В древности были распространены римские додекаэдры — бронзовые объекты, составленные из 12 пятиугольников, однако истинное назначение предметов до сих пор не выяснено. Сегодня наиболее очевидным реальным додекаэдром является игральная кость, которая выступает в качестве генератора случайных чисел для настольных ролевых игр.
В природе форма пятиугольника не встречается, однако некоторые организмы, например иглокожие, обладают пентасимметрией. Кроме того, в природе не существует кристаллов, грани которых были бы пятиугольными.
Периметр пентагона
Периметр любой геометрической фигуры — это сумма длин всех сторон. Пентагон имеет пять равных сторон, поэтому его периметр находится по простой формуле:
P = 5 a,
где a – длина одной стороны.
Сторона пятиугольника и радиусы вписанной r и описанной R окружностей приблизительно соотносятся как:
- a = 1,1756 R
- a = 1,4131 r
Таким образом, алгоритм нашего калькулятора позволяет рассчитать периметр пентагона, зная только один из трех параметров на выбор:
- сторона;
- радиус описанной окружности;
- радиус вписанной окружности.
Рассмотрим пару примеров на определение периметра правильного пятиугольника.
Примеры из жизни
Пентагон
Пентагон — всемирно известное здание, в котором располагается штаб министерства обороны США. Объект получил название благодаря своей форме, так как здание геометрически является правильным пятиугольником. Давайте посчитаем периметр Пентагона. Согласно данным из Википедии, каждая сторона здания равна 281,05 м. Зная сторону, мы можем легко вычислить периметр штаба:
P = 1 405,25
Таким образом, суммарная длина сторон Пентагона составляет практически полтора километра.
Школьная задача
Допустим, вам нужно определить периметр правильного пятиугольника, зная, что радиус описанной вокруг него окружности равен 5 см. Вы можете последовательно использовать приведенные выше соотношения для вычисления стороны пентагона, а затем и его периметра. Давайте сэкономим время и просто введем значение в форму калькулятора «Радиус описанной окружности R».
P = 29,38
Помимо периметра, калькулятор определил значения стороны пентагона, а также радиус вписанной в него окружности.
Заключение
Правильный пятиугольник — достаточно редкая в человеческой повседневности и природе фигура. Впрочем, вычисление параметров пентагона может понадобиться вам при решении школьных задач или рабочих вопросов. Используйте для этих целей наш онлайн-калькулятор, который определяет периметр пятиугольника, зная только один параметр фигуры.
