Как найти периметр равностороннего ромба

В данной публикации мы рассмотрим, каким образом можно посчитать периметр ромба и разберем примеры решения задач.

Формула вычисления периметра

1. По длине стороны

Периметр (P) ромба равняется сумме длин всех его сторон.

P = a + a + a + a

Т.к. все стороны данной геометрической фигуры равны, формулу можно представить в следующем виде (сторона умноженная на 4):

P = 4*a

2. По длине диагоналей

Диагонали любого ромба пересекаются под углом 90° и в точке пересечения делятся пополам, т.е.:

• AO=OC=d₁/2
• BO=OD=d₂/2

Диагонали делят ромб на 4 равных прямоугольных треугольника: AOB, AOD, BOC и DOC. Давайте подробнее остановимся на AOB.

Найти сторону AB, которая одновременно является гипотенузой прямоугольника и стороной ромба, можно, воспользовавшись теоремой Пифагора:

AB² = AO² + OB²

Подставляем в эту формулу длины катетов, выраженные через половины диагоналей, и получаем:

AB² = (d₁/2)² + (d₂/2)², или

Таким образом, периметр равняется:

Примеры задач

Задание 1
Найдите периметр ромба, если длина его стороны составляет 7 см.

Решение:
Используем первую формулу, подставив в нее известное значение: P = 4 * 7 см = 27 см.

Задание 2
Периметр ромба равен 44 см. Найдите сторону фигуры.

Решение:
Как мы знаем, P = 4*a. Следовательно, чтобы найти одну сторону (a), необходимо периметр разделить на четыре: a = P/4 = 44 см / 4 = 11 см.

Задание 3
Найдите периметр ромба, если известны его диагонали: 6 и 8 см.

Решение:
Воспользовавшись формулой, в которой задействованы длины диагоналей, получаем:

Содержание:

• Определения
• Формулы периметра основных геометрических фигур

Определения

Периметр имеет ту же размерность величин, что и длина. Иногда периметром называют границу геометрической фигуры.
Чаще всего этот термин применяется к треугольнику и многоугольникам и в этом случае означает сумму длин всех сторон фигуры.
То есть периметр – это сумма длин сторон какой-либо геометрической фигуры.

Формулы периметра основных геометрических фигур

Периметр треугольника

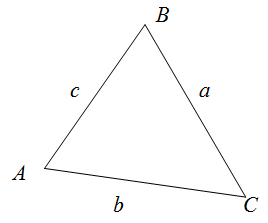
Чтобы найти периметр треугольника $ABC$,
необходимо сложить длины всех его сторон.

Читать дальше: формула периметра треугольника и примеры решений →

Периметр круга

Чтобы найти периметр круга, необходимо вычислить длину окружности, которая его ограничивает.

Для нахождения длины окружности можно использовать одну из формул

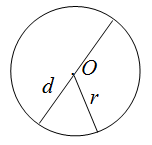
Читать дальше: формула периметра круга и примеры решений →

Периметр квадрата

Чтобы найти периметр квадрата, необходимо длину его стороны умножить на четыре.

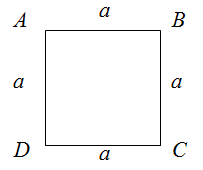
Читать дальше: формула периметра квадрата и примеры решений →

Периметр прямоугольника

Чтобы найти периметр прямоугольника, нужно сумму его ширины и длины умножить на два.

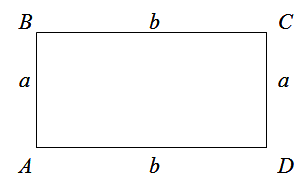
Читать дальше: формула периметра прямоугольника и примеры решений →

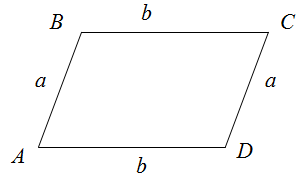
Периметр параллелограмма

Чтобы найти периметр параллелограмма, нужно сумму двух непараллельных сторон умножить на два.

Читать дальше: формула периметра параллелограмма и примеры решений →

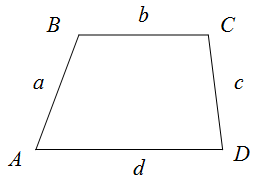
Периметр трапеции

Чтобы найти периметр трапеции необходимо найти сумму длин её сторон.

Читать дальше: формула периметра трапеции и примеры решений →

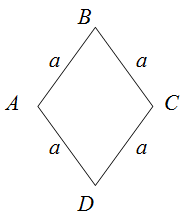
Периметр ромба

Чтобы найти периметр ромба, необходимо длину его стороны умножить на четыре.

Читать дальше: формула периметра ромба и примеры решений →

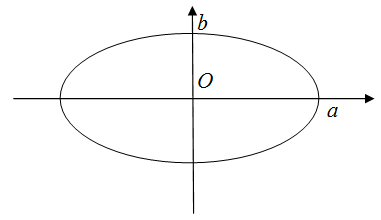
Периметр эллипса

Чтобы найти периметр эллипса
$frac{x^{2}}{a^{2}}+frac{y^{2}}{b^{2}}=1$, нужно воспользоваться формулой

Читать дальше: формула периметра эллипса и примеры решений →

• Как найти периметр треугольника
• Как найти периметр трапеции
• Как найти периметр ромба
• Как найти периметр эллипса
• Как найти периметр многоугольника
• Как найти периметр прямоугольного треугольника
• Как найти периметр равнобедренного треугольника
• Как найти периметр равностороннего треугольника
• Как найти периметр круга
• Как найти длину окружности
• Как найти периметр квадрата
• Как найти периметр прямоугольника
• Как найти периметр параллелограмма

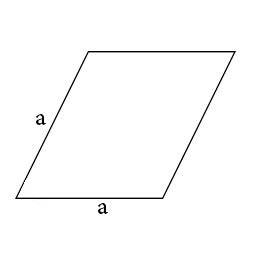
Для того, что бы вычислить периметр ромба нам необходимо знать длину его стороны. Как только нам стала известна длина одной из его сторон и зная что ромб состоит из четырех одинаковых по своей дине стороны мы можем легко вычислить его периметр по нижеследующей формуле:

P=a+a+a+a

P = a4

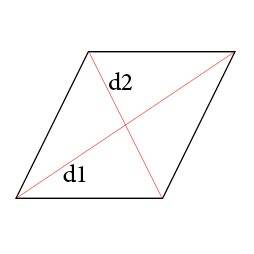
Так же периметр ромба можно вычислить зная длину его диагоналей, т.к. при пересечении диагонали образуют угол равный 90° и тем самым делят ромб на четыре прямоугольных треугольника. Далее используя теорему Пифагора в которой говориться , что квадрат гипотенузы равен сумме квадратов катетов, мы с легкостью сможем высчитать периметр ромба по следующей формуле

Периметр ромба калькулятор онлайн умеет вычислять периметр двумя способами:

1. По стороне ромба.
2. По диагоналям ромба.

Сделав расчет периметра на этом онлайн калькуляторе Вы получите не только ответ, но и детальное, пошаговое решение с выводом формул и промежуточных действий.

Периметр ромба- это сумма всех его сторон. 
Так как у ромба все стороны равны, то периметр равен длине любой его стороны, умноженной на четыре.

Как найти периметр ромба?

Найти периметр ромба очень просто на нашем онлайн калькуляторе. Так же периметр может быть найден самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.

1) По стороне ромба

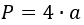
где a- любая из равных сторон ромба.

2) По двум диагонялям

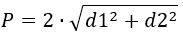
где d1,d2 – диагонали ромба.

Скачать все формулы в формате Word

Формулы периметра геометрических фигур

Формула периметра треугольника

Периметр треугольника ∆ ABC равен сумме длин его сторон

Формулы периметра квадрата

Периметр квадрата равен произведению длины его стороны на четыре.

Периметр квадрата равен произведению длины его диагонали на два корня из двух.

Формула периметра прямоугольника

Периметр прямоугольника ABCD равен удвоенной сумме сторон, прилежащих к одному углу.

Формула периметра параллелограмма

Периметр параллелограмма ABCD равен удвоенной сумме сторон, прилежащих к одному углу

Формула периметра ромба

Периметр ромба равен произведению длины его стороны на четыре.

Формула периметра трапеции

Периметр трапеции равен сумме длин ее сторон.

Формулы длины окружности.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Как найти периметр квадрата, прямоугольника, параллелограмма, трапеции, ромба, эллипса, многоугольника

Вы будете перенаправлены на Автор24

Периметр любой геометрической фигур на плоскости определяется как сумма длин всех его сторон. В этой статье, на примере задач, мы приведем формулы для нахождения периметров квадрата, прямоугольника, параллелограмма, трапеции, ромба, многоугольника и эллипса.

Периметр квадрата

Квадратом будем назвать такую геометрическую фигуру, которая состоит из четырех равных сторон, все углы которой прямые (рис. 1).

Найти периметр квадрата, если его сторона равняется $α$.

Так как все 4 стороны квадрата равны между собой, то, по определению периметра, получим

Вывод: Для нахождения периметра квадрата надо длину его стоны умножить на $4.$

Периметр прямоугольника

Прямоугольником будем назвать такую геометрическую фигуру, которая состоит из четырех сторон, причем противоположные стороны равны между собой, все углы которой прямые (рис. 2).

Найти периметр прямоугольника, если его смежные стороны равняются $α$ и $β$.

Так как противоположные стороны равняются между собой, то

Готовые работы на аналогичную тему

Вывод: Для нахождения периметра прямоугольника надо сумму длин его смежных сторон умножить на $2.$

Периметр параллелограмма

Параллелограммом будем назвать такую геометрическую фигуру, которая состоит из четырех сторон, причем противоположные стороны равны между собой и параллельны друг другу (рис. 3).

Найти периметр параллелограмма, если его смежные стороны равняются $α$ и $β$.

Так как противоположные стороны равняются между собой, то

Вывод: Для нахождения периметра параллелограмма надо сумму длин его смежных сторон умножить на $2.$

Периметр трапеции

Трапецией будем назвать такую геометрическую фигуру, которая состоит из четырех сторон, причем 2 противоположные стороны, которые называются основаниями, параллельны друг другу (рис. 4).

Найти периметр трапеции, если его стороны равняются $α$, $β$, $γ$ и $δ$.

По определению периметра плоской геометрической фигуры получим, что

Вывод: Для нахождения периметра трапеции надо сложить все длины его сторон.

Периметр ромба

Ромбом будем назвать такой параллелограмм, у которого все стороны равны между собой (рис. 5).

Найти периметр ромба, если его сторона равняется $α$.

Так как все 4 стороны ромба равны между собой, то, по определению периметра, получим

Вывод: Для нахождения периметра ромба надо длину его стоны умножить на $4.$

Периметр многоугольника

Отметим, что все фигуры, рассмотренные выше, являются многоугольниками, а именно четырехугольниками. Поэтому можем рассмотреть более обще понятие, а именно понятие -угольника.

$n$-угольником будем назвать такую геометрическую фигуру, которая состоит из $n$ непересекающихся сторон и $n$ углов. (рис. 6).

Найти периметр $n$-угольника, если его стороны равняются $α_1$, $α_2$,…, $α_n$.

По определению периметра плоской геометрической фигуры получим, что

Вывод: Для нахождения периметра -угольника надо сложить все длины его сторон.

Здесь можно выделить периметр правильного $n$-угольника, то есть $n$-угольника, у которого все стороны равняются между собой.

Найти периметр правильного $n$-угольника, если его сторона равняется $α$.

Так как все $n$ сторон правильного $n$-угольника равны между собой, то, по определению периметра, получим

Вывод: Для нахождения периметра правильного $n$-угольника надо длину его стороны умножить на $n$

Периметр эллипса

Здесь просто введем формулу, для вычисления периметра (или еще иначе длины) эллипса. Пусть нам дан эллипс, как на рисунке 7.

Тогда периметр эллипса равняется

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 13 07 2021

Эксперт по предмету «Геометрия»

Работаем по будням с 10:00 до 20:00 по Мск

. и многие другие.
Успешной учебы! Будем рады вам помочь!

Как найти периметр фигуры

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Определение периметра

Периметр — это сумма длин всех сторон многоугольника.

Какой буквой обозначается периметр? Заглавной латинской P. Под обозначением P удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.

В чем измеряется периметр? В тех же единицах измерения, что и длина — например, миллиметр, сантиметр, метр, фут, дюйм, локоть и др.

Если в условиях задачки длины сторон переданы в разных единицах длины, мы не сможем узнать периметр фигуры. Для правильного решения нужно перевести все данные в одну единицу измерения.

Формулы нахождения периметра

Как мы только что узнали, периметр — это сумма длин всех сторон многоугольника. А значит, чтобы его найти, нам надо знать длины этих сторон. Давайте посмотрим, как найти периметр, на примерах нескольких фигур.

Равносторонний многоугольник

У равностороннего треугольника все стороны равны. А значит, периметр равностороннего треугольника можно найти как произведение длины стороны на их количество, т. е. на 3.

P = 3 ⋅ a, где a — длина стороны.

Периметр любого другого равностороннего многоугольника можно найти тем же способом: умножив длину его стороны на их количество. Например, у квадрата и ромба все стороны равны, а значит, их периметр можно найти по формуле P = 4 ⋅ a, где a — длина стороны.

А формула для любого равностороннего n-угольника будет такая: P = n ⋅ a, где a — длина стороны, n — количество сторон.

Прямоугольник и параллелограмм

У прямоугольника и параллелограмма противоположные стороны равны, а значит, найти их периметр легко, зная две соседние стороны.

P = 2 ⋅ (a + b), где a — одна сторона, b — соседняя сторона.

Окружность

У окружности нет периметра, потому что это не многоугольник. Но у нее есть длина, которую можно найти, зная радиус. Длина окружности — это произведение пи на два радиуса или произведение пи на диаметр.

L = d ⋅ π = 2 ⋅ r ⋅ π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она приблизительно равна 3,14.

Можно выучить все формулы, а можно, запомнив определение о сумме всех сторон, каждый раз проявлять смекалку и вычислять самостоятельно. Давайте потренируемся, как определять периметр фигур!

Решение задач

Площадь прямоугольника равна 80 см 2 , длина составляет 10 см. Чему равен периметр фигуры?

• Для использования формулы P = 2 × (a + b), нам нужно найти ширину;
• Так как S = a × b, для поиска одной стороны необходимо разделить площадь на известную сторону: 80 : 10 = 8 см;
• Далее подставляем известные данные в формулу: (10 + 8) × 2 = 36 см;

Равнобедренный треугольник имеет периметр 40 см, длина его основания составляет 6 см. Какую длину будут иметь две другие стороны?

• Мы знаем, что периметр — это сумма длин всех сторон, а значит, если вычесть из данного периметра сторону основания — получим сумму двух оставшихся сторон: 40 − 6 = 34 см;
• Известно, что равнобедренный треугольник имеет две равные стороны;
• Далее делим получившуюся сумму на два: 34 : 2 = 17 см;

Ответ: две другие стороны равны по 17 см.

Радиус окружности равен периметру равностороннего пятиугольника со стороной 4 см. Найдите длину окружности.

• Периметр равностороннего пятиугольника равен 4 × 5 = 20 см, значит, радиус окружности равен 20 см;
• Длина окружности равна π × 2 × 20 = 40π см;

Еще больше практических заданий — на курсах по математике в онлайн-школе Skysmart!

[spoiler title=”источники:”]

http://spravochnick.ru/geometriya/ploschad_formuly_ploschadi/kak_nayti_perimetr_kvadrata_pryamougolnika_parallelogramma_trapecii_romba_ellipsa_mnogougolnika/

http://skysmart.ru/articles/mathematic/perimetr-figury

[/spoiler]