Формулы периметра треугольника

Как найти периметр любого треугольника? Существует
множество способов сделать это, но мы расскажем про
основные. В этой статье вы узнаете, как найти периметр
любого треугольника через известные величины, по формулам.
Ⅰ. Через площадь и радиус вписанной окружности
Известно: площадь и радиус вписанной окружности треугольника.
Чтобы найти периметр любого треугольника,
нужно две площади треугольника разделить
на радиус вписанной окружности.
Как видим, для этой формулы нужно знать всего
лишь радиус вписанной окружности и площадь.
Ⅱ. Через три стороны
Известно: три стороны треугольника.
Чтобы найти периметр любого треугольника,
нужно сложить все стороны треугольника.
Результатом и будет периметр.
Это самая простая формула.
Ⅲ. Через Теорему Косинусов
Известно: две стороны и угол между ними.
Чтобы найти периметр любого треугольника,
нужно для начала найти третью сторону треугольника,
затем косинус угла, если косинус неизвестен.
Это формулу удобней применить,
если вам известны две стороны
и косинус между ними.
Нахождение периметра треугольника: формула и задачи
В данной публикации мы рассмотрим, каким образом можно посчитать периметр треугольника и разберем примеры решения задач.
Формула вычисления периметра
Периметр (P) любого треугольника равняется сумме длин всех его сторон.
P = a + b + c

Периметр равнобедренного треугольника
Равнобедренным называют треугольник, у которого две боковые стороны равны (примем их за b). Сторона a, имеющая отличную от боковых длину, является основанием. Таким образом, периметр можно считать так:
P = a + 2b
Периметр равностороннего треугольника
Равносторонним или правильным называется треугольник, у которого все стороны равны (примем ее за a). Периметр такой фигуры вычисляется так:
P = 3a
Примеры задач
Задание 1
Найдите периметр треугольника, если его стороны равны: 3, 4 и 5 см.
Решение:
Подставляем в формулу известные по условиям задачи величины и получаем:
P = 3 см + 4 см + 5 см = 12 см.
Задание 2
Найдите периметр равнобедренного треугольника, если его основание равняется 10 см, а боковая сторона- 8 см.
Решение:
Как мы знаем, боковые стороны равнобедренного треугольника равны, следовательно:
P = 10 см + 2 ⋅ 8 см = 26 см.
Как найти периметр треугольника

О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение
Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской буквой P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах и ходе решении.
Важно, чтобы все параметры были переданы в одной единице длины, иначе мы не сможем подсчитать результат. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
В чем измеряется периметр:
Как узнать периметр треугольника
Рассмотрим какие существуют формулы, и при каких известных исходных данных их можно применять.
Если известны три стороны, то периметр треугольника равен их сумме. Этот способ проходят во втором классе.
P = a + b + c, где a, b, c — длина стороны.
Если известна площадь и радиус вписанной окружности:
P = 2 * S : r, где S — площадь, r — радиус вписанной окружности.
Если известны две стороны и угол между ними, вычислить периметр треугольника можно так:
P = √ b 2 + с 2 – 2 * b * с * cosα + (b + с), где b, с — известные стороны, α — угол между известными сторонами.
Если известна одна сторона в равностороннем треугольнике:
P = 3 * a, где a — длина стороны.
Все стороны в равносторонней фигуре равны.
Если известна боковая сторона и основание в равнобедренном треугольнике:
P = 2 * a + b, где a — боковая сторона, b — основание.
Боковые стороны в равнобедренной фигуре равны.
Если известна боковая сторона и высота в равнобедренном треугольнике:
P = 2 * (√ a 2 + h 2 ) + 2 * a, где a — боковая сторона, h — высота.
Высотой принято называть отрезок, который вышел из вершины и опустился на основание. В равнобедренной фигуре высота делит основание пополам.
Если известны катеты в прямоугольном треугольнике:
P = √ a 2 + b 2 + (a + b), где a, b — катеты.
Катет — одна из двух сторон, которые образуют прямой угол.
Если известны катет и гипотенуза в прямоугольном треугольнике:
P = √ c 2 – a 2 + (a + c), где a — любой катет, c — гипотенуза.
Гипотенуза — сторона, которая лежит напротив прямого угла.
Скачать онлайн таблицу
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/perimetr-treugolnika
[/spoiler]
Периметр равностороннего треугольника по длине биссектрисы угла Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Длина биссектрисы равностороннего треугольника: 7 метр –> 7 метр Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
24.2487113059643 метр –> Конверсия не требуется
9 Периметр равностороннего треугольника Калькуляторы
Периметр равностороннего треугольника по длине биссектрисы угла формула
Периметр равностороннего треугольника = 2*sqrt(3)*Длина биссектрисы равностороннего треугольника
P = 2*sqrt(3)*lAngle Bisector
Основные определения
Наверное, каждый из нас сталкивался с треугольником. Это могло быть в школе, вузах, колледжах, на работе, во время помощи детям. Треугольник – это одна из самых простых геометрических фигур, но в то же время она выполняет очень важную роль. Множество свойств хранит треугольник. Но сегодня не будем вдаваться в подробности, а поговорим про периметр и порешаем задачи по нахождению его.
Если мы отметим на плоскости 3 точки и проведём к ним линии, то как раз получим треугольник.
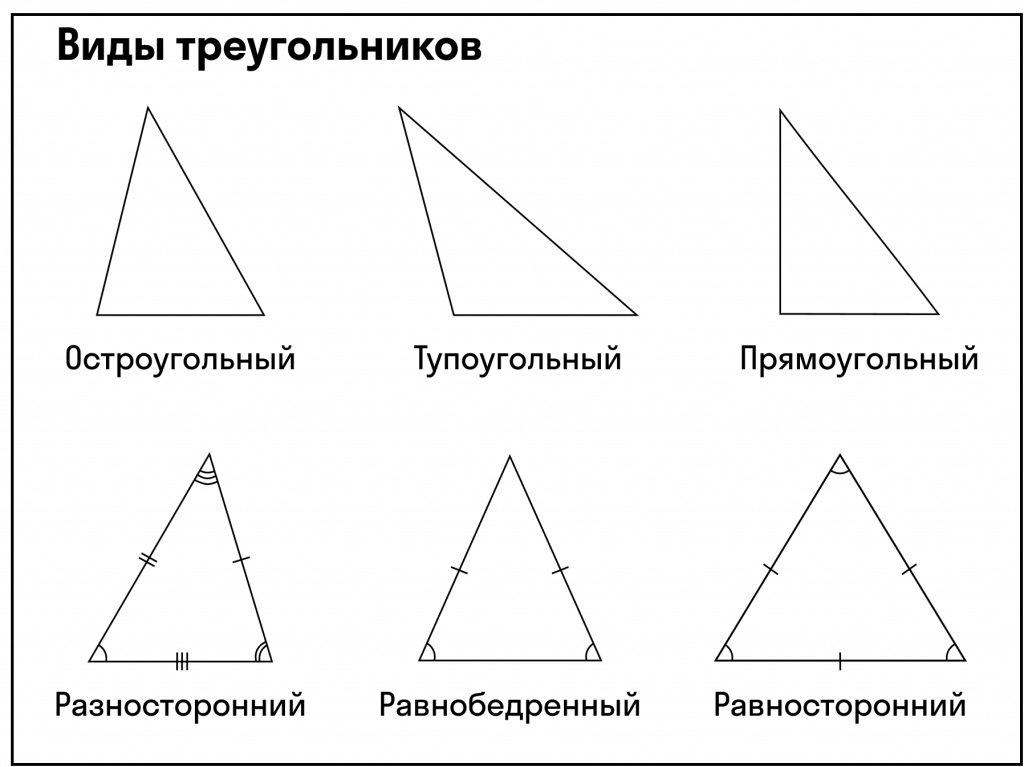
Понятия
Треугольник – это геометрическая фигура, состоящая из трёх точек, которые соединены отрезками – сторонами. В зависимости от отношений между сторонами фигуры, то они бывают равносторонними, разносторонними и равнобедренными (р/б – равнобедренный, р/с – равносторонний).
Вершины треугольника – это точки, где соединяются 2 стороны фигуры.
Р/б треугольник – это треугольник у которого две стороны равны, но не равны третьей.
Р/с треугольник – это треугольник, у которого все стороны равны между собой.
Разносторонний треугольник – это треугольник, у которого все стороны не равны между собой.
Прямоугольный треугольник — это треугольник, у у которого один угол равен 90о. Самая длинная сторона называется гипотенузой, а две другие катетами.
Формула нахождения периметра
Из определения следует, что периметр геометрической фигуры – это сумма длин всех сторон, и треугольник не стал исключением. Общая формула имеет вид: Р = а + b + с. Периметр будет обозначаться Р. а, b и с — стороны треугольника. Решим задачу №1.
Задача 1
Пусть нам дан треугольник со сторонами 13 см, 15 см, 12 см. Нужно найти периметр данного треугольника.
Решение: [P=13+15+12=40] см.
Ответ: 40 см.
Периметр разностороннего треугольника
В прошлой задаче мы как раз нашли периметр разностороннего треугольника. Решим похожую задачу №2
Задача 2
Дан треугольник со сторонами 25 дм, 30 дм, 15 дм. Найдите периметр треугольника. Ответ выразите в метрах.
Решение:
P = 30 + 25 + 15 = 70 дм
70 : 10 = 7 м
Ответ: 7 м.
Периметр равнобедренного треугольника
Так как в р/б треугольнике 2 стороны равны (боковые), то формулу нахождения можно представить как: P = 2a + b. Решим 2 задачи.
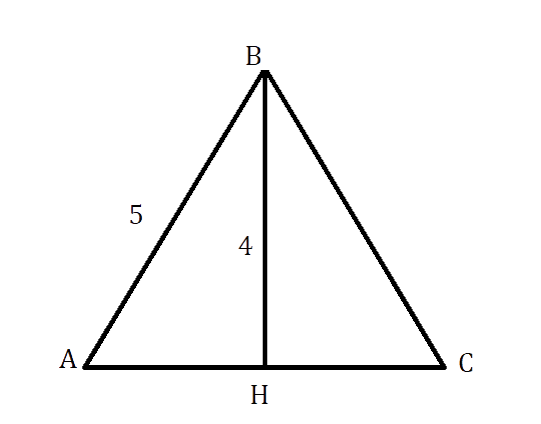
Задачи 3 — 4
Дан равнобедренный треугольник АВС с биссектрисой, проведённой к основанию и равной 4 см, а также с боковой
стороной, равной 5 см. Найдите периметр данного треугольника.
Решение:
Так как ВН – биссектриса р/б треугольника АВС, то она является как высотой, так и медианой. Следовательно, ΔАВН прямоугольный и АН = НС.
В ΔАВН по теореме Пифагора [A H^{2}=A B^{2}-B H^{2}=25-16=9]см
АН = НС = √9 = 3 см
АС = АН + НС = 3 + 3 = 6 см
Р = 6 + 2*5 = 16 см
Ответ: 16 см.
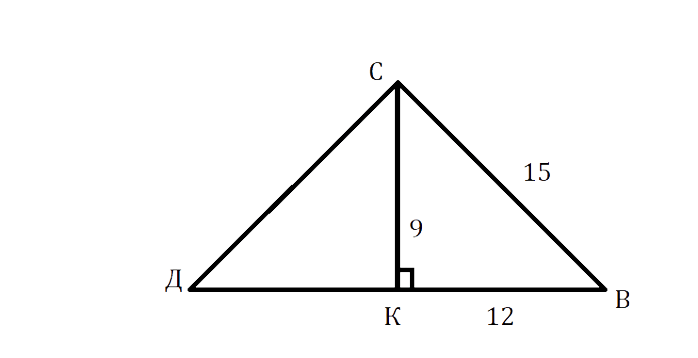
В треугольнике ДСВ ДС = СВ = 15 см, высота СК = 9 см. Найдите периметр этого треугольника.
Решение:
В ΔСКД по теореме Пифагора:
[text { ДК² }=text { ДС }^{2}-mathrm{CK}^{2}=225-81=144]см
ДК = √144 = 12 см.
Так как СК — высота в р/б треугольнике, проведённая к основанию, то она является медианой, следовательно, ДВ = ДК + КВ = 12 + 12 = 24 см.
Р = ДС + СВ + ДВ = 15 + 15 + 24 = 54 см.
Ответ: 54 см.
Нет времени решать самому?
Наши эксперты помогут!
Периметр равностороннего треугольника
А это один из самых “хороших” треугольников, его ещё называют правильным, так как все стороны и углы равны между собой. Формула нахождения периметра будет иметь вид: P = 3a.
Задачи 5 — 6
Дан равносторонний треугольник со стороной а = 13. Найдите периметр этого треугольника.
Решение:
Р = 3а = 3 * 13 = 39
Ответ: 39.
В равностороннем треугольнике АВС есть стороны: АВ = АС = СВ = 15 см, Найдите периметр данного треугольника.
Решение:
Р = 3АВ = 15 * 3 = 45 см.
Ответ: 45 см.
Периметр прямоугольного треугольника
Вычисляем по стандартной формуле: Р = а + в + с. Но у такого вида треугольников есть огромное преимущество – применение теоремы Пифагора.
Задачи 7 — 8
Дан прямоугольный треугольник с катетами а = 6 и в = 8. Найдите периметр.
Решение:
По теореме Пифагора: [c^{2}=в^{2}+a^{2}=64+36=100]
с = √100 = 10
Р = а + в + с = 6 + 8 + 10 = 24
Ответ: 24.
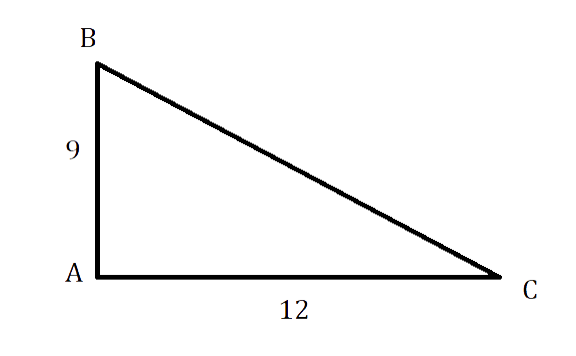
В прямоугольном треугольнике АВС, [angle mathrm{A}=90^{circ}, mathrm{AB}=9 mathrm{~см}, mathrm{AC} = 12см]. Надо найти периметр и площадь АВС.
Решение
По теореме Пифагора в ΔАВС:
[mathrm{CB}^{2}=mathrm{AC}^{2}+A mathrm{C}^{2}=144+81=225 mathrm{~см}]
СВ = √225 = 15 см
S = (АС * АВ) : 2 = (9 * 12) : 2 = 54 см
P = 15 + 9 + 12 = 36 см
Ответ: 36 см; 54 см.

kirillderbilov
+10
Ответ дан
2 года назад
Геометрия
5 – 9 классы
Биссектриса равностороннего треугольника равна 21√3.Найдите периметр этого треугольника. Помогите пожалуйста.!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Ответ проверен экспертом
1/5
(4 оценки)
5

manyny06
2 года назад
Светило науки – 24673 ответа – 41155 раз оказано помощи
Ответ:
решение смотри на фотографии

Оцените пользу ответа
Ответ
1.5/5
(2 оценки)
1

Iutcahcihhia
2 года назад
Светило науки – 183 ответа – 0 раз оказано помощи
3*21√3/cos30=126
21√3/cos30-длина стороны треугольника
ответ 126
Оцените пользу ответа

Мозг
Отвечающий
Остались вопросы?
Задать вопрос
Содержание:
- Формула
- Примеры вычисления периметра равностороннего треугольника
Формула
Чтобы найти периметр равностороннего треугольника, надо длину его стороны умножить на три.
Периметр равностороннего треугольника – это сумма длин его сторон. У равностороннего треугольника
все стороны равны. Поэтому чтобы найти периметр равностороннего треугольника
$ABC$, со стороной
$a$ нужно воспользоваться формулой
$$P_{Delta A B C}=a+a+a=3 a$$
Примеры вычисления периметра равностороннего треугольника
Пример
Задание. Найти периметр треугольника
$ABC$ со стороной, равной 5 дм.
Решение. Воспользуемся формулой для нахождения периметра равностороннего треугольника:
$$P_{Delta A B C}=3a$$
Тогда искомый периметр равен:
$P_{Delta A B C}=3 cdot 5=15$ (дм)
Ответ. $P_{Delta A B C}=15$ (дм)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Периметр равностороннего треугольника
$ABC$ равен
27 см. Найти длины его стороны.
Решение. Периметр равностороннего треугольника вычисляется по формуле:
$$P_{Delta A B C}=3 a$$
Подставим в нее заданное значение периметра и выразим из полученного уравнения искомую длину
$a$:
$27=3 a Rightarrow a=27: 3=9$ (см)
Ответ. $a=9$ (см)
Читать дальше: как найти периметр круга.

