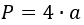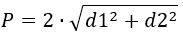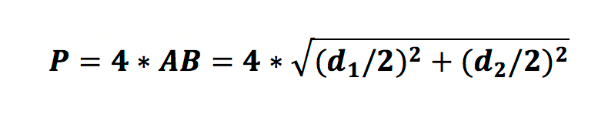В данной публикации мы рассмотрим, каким образом можно посчитать периметр ромба и разберем примеры решения задач.
- Формула вычисления периметра
- Примеры задач
Формула вычисления периметра
1. По длине стороны
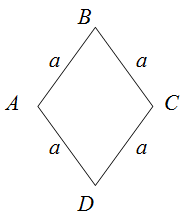
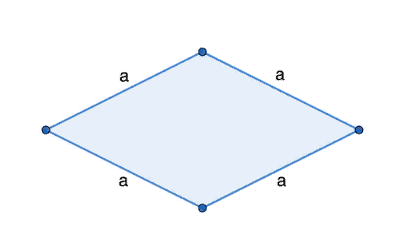
Периметр (P) ромба равняется сумме длин всех его сторон.
P = a + a + a + a
Т.к. все стороны данной геометрической фигуры равны, формулу можно представить в следующем виде (сторона умноженная на 4):
P = 4*a
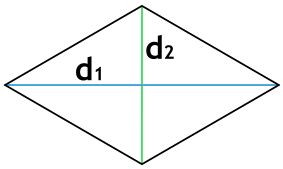
2. По длине диагоналей
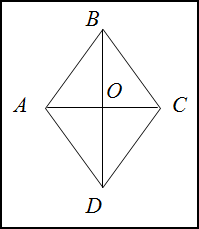
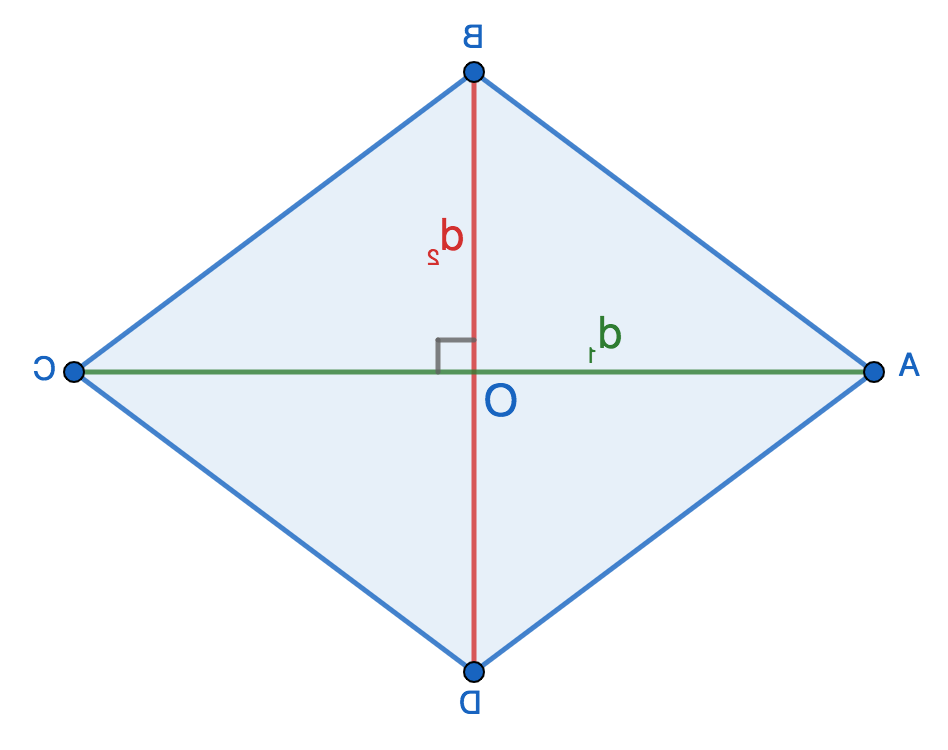
Диагонали любого ромба пересекаются под углом 90° и в точке пересечения делятся пополам, т.е.:
- AO=OC=d1/2
- BO=OD=d2/2
Диагонали делят ромб на 4 равных прямоугольных треугольника: AOB, AOD, BOC и DOC. Давайте подробнее остановимся на AOB.
Найти сторону AB, которая одновременно является гипотенузой прямоугольника и стороной ромба, можно, воспользовавшись теоремой Пифагора:
AB2 = AO2 + OB2
Подставляем в эту формулу длины катетов, выраженные через половины диагоналей, и получаем:
AB2 = (d1/2)2 + (d2/2)2, или
Таким образом, периметр равняется:
Примеры задач
Задание 1
Найдите периметр ромба, если длина его стороны составляет 7 см.
Решение:
Используем первую формулу, подставив в нее известное значение: P = 4 * 7 см = 27 см.
Задание 2
Периметр ромба равен 44 см. Найдите сторону фигуры.
Решение:
Как мы знаем, P = 4*a. Следовательно, чтобы найти одну сторону (a), необходимо периметр разделить на четыре: a = P/4 = 44 см / 4 = 11 см.
Задание 3
Найдите периметр ромба, если известны его диагонали: 6 и 8 см.
Решение:
Воспользовавшись формулой, в которой задействованы длины диагоналей, получаем:
Содержание:
- Формула
- Примеры вычисления периметра ромба
Формула
Чтобы найти периметр ромба, необходимо длину его стороны умножить на четыре.
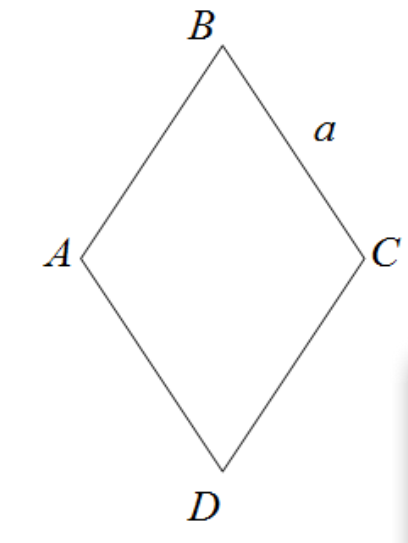
По определению ромб – это параллелограмм, у которого все стороны равны. Таким образом, формула для нахождения периметра ромба
$ABCD$ со стороной $a$ имеет вид:
$$P_{Delta A B C D}=a+a+a+a=4 a$$
Примеры вычисления периметра ромба
Пример
Задание. Найти периметр ромба
$ABCD$ со стороной $a=2,5$ дм.
Решение. Для нахождения периметра ромба
$ABCD$ воспользуемся формулой:
$$P_{Delta A B C D}=4 a$$
Подставляя в неё $a=2,5$ дм, получим:
$P_{Delta A B C D}=4 cdot 2,5=10$ (дм)
Ответ. $P_{Delta A B C D}=10$ (дм)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти периметр ромба
$ABCD$, если его диагонали равны соответственно
$AC=6$ м и
$BD=8$ м.
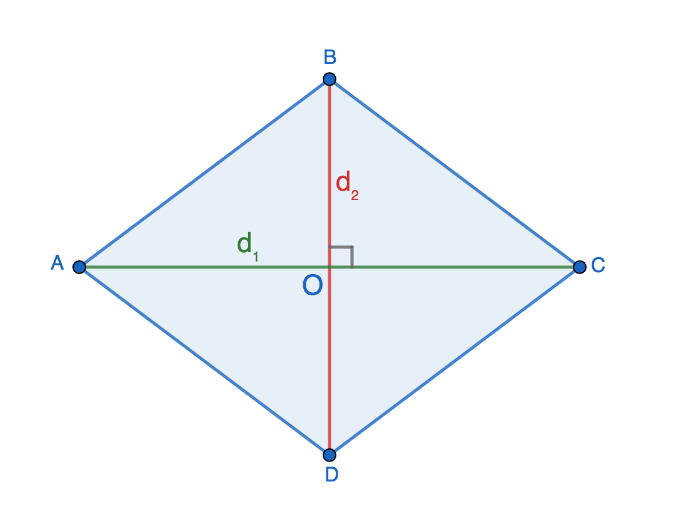
Решение. Сделаем рисунок.
Обозначим
$O$ точку пересечения диагоналей. По свойству
ромба его диагонали пересекаются под прямым углом и в точке пересечения делятся пополам. Рассмотрим треугольник $ABO$. Он прямоугольный
$angle 0=90^{circ}$. Его катеты
$A O=frac{A C}{2}=6: 2=3$ (м) и
$B O=frac{B D}{2}=8: 2=4$ (м). Тогда по теореме Пифагора сторона
$AC$ равна:
$A C=sqrt{A O^{2}+B O^{2}}=sqrt{3^{2}+4^{2}}=sqrt{9+16}=sqrt{25}=5$ (м)
Искомый периметр
$P_{Delta A B C D}=4 cdot 5=20$ (м)
Ответ. $P_{Delta A B C D}=20$ (м)
Читать дальше: как найти периметр эллипса.
Чтобы найти периметр ромба достаточно знать его сторону или диагонали и воспользоваться простейшей формулой. Чтобы облегчить эту задачу мы создали онлайн калькулятор, который мгновенно найдет периметр.
У нас вы также можете рассчитать периметр других четырехугольников: квадрата, прямоугольника, параллелограмма, трапеции.
Содержание:
- калькулятор периметра ромба
- формула периметра ромба через сторону
- формула периметра ромба через диагонали
- примеры задач
Ромб – параллелограмм, у которого все стороны равны.
Формула периметра ромба через сторону
{P = 4a}
a – сторона ромба
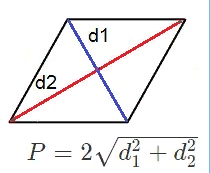
Формула периметра ромба через диагонали
{P = 2 sqrt{{d_1}^2+{d_2}^2}}
d1 и d2 – диагонали ромба
Примеры задач на нахождение периметра ромба
Задача 1
Найдите периметр ромба, если его диагонали равны 60см и 80см.
Решение
Для решения задачи используем вторую формулу.
P = 2 sqrt{{d_1}^2+{d_2}^2} = 2 sqrt{{60}^2+{80}^2} = 2 sqrt{3600+6400} = 2 sqrt{10000} = 2 cdot 100 = 200 : см
Ответ: 200 см
Проверим ответ на калькуляторе .
Задача 2
Найти периметр ромба, если его сторона равна 12см.
Решение
Воспользуемся первой формулой. Подставим в нее значение стороны ромба и вычислим его периметр:
P = 4a = 4 cdot 12 = 48 : см
Ответ: 48 см
Проверим ответ с использованием калькулятора .
Периметр ромба калькулятор онлайн умеет вычислять периметр двумя способами:
- По стороне ромба.
- По диагоналям ромба.
Сделав расчет периметра на этом онлайн калькуляторе Вы получите не только ответ, но и детальное, пошаговое решение с выводом формул и промежуточных действий.
Периметр ромба- это сумма всех его сторон.
Так как у ромба все стороны равны, то периметр равен длине любой его стороны, умноженной на четыре.
Как найти периметр ромба?
Найти периметр ромба очень просто на нашем онлайн калькуляторе. Так же периметр может быть найден самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.
1) По стороне ромба
где a- любая из равных сторон ромба.
2) По двум диагонялям
где d1,d2 – диагонали ромба.
Скачать все формулы в формате Word
Что нужно знать о периметре ромба — основные сведения
Содержание:
-
Основные сведения о фигуре ромб
- Понятие периметра ромба
-
Способы нахождения периметра
- Через стороны
- Через длину диагонали
- Формулы для каждого способа
- Примеры решения задач
Основные сведения о фигуре ромб
Рассмотрим особый вид параллелограмма, для которого характерны следующие признаки:
- Две стороны, являющиеся смежными, равны по величине.
- Проведенные из углов диагонали пересекаются в центре фигуры таким образом, что образуют прямой угол.
- Определенная диагональ разделяет углы, которые она соединяет, пополам.
По этим признакам можно четко определить, когда параллелограмм является ромбом.
Ромбом называется геометрическая фигура, которая является параллелограммом и имеет все четыре стороны равной длины.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Произошло название от греческого слова ῥόμβος либо латинского rombus. В переводе они означают «бубен».
При этом геометрическими свойствами ромба являются:
- Поскольку ромб — параллелограмм, его стороны, лежащие противоположно, имеют равные величины и попарную параллельность. Кроме этого, для всех ромбов характерно равенство противоположных углов, а также факт, что соседние с ними углы составляют в сумме 180о.
- С помощью проведения диагоналей можно разделить ромб на четыре треугольника, имеющих прямые углы. При этом диагонали пересекутся в центре фигуры в точке, которая разделит их пополам.
- Вышеуказанные диагонали будут биссектрисами углов ромба.
- Если длину диагоналей возвести в квадрат и сложить эти квадраты, то получишь квадрат стороны, увеличенный в 4 раза (данное свойство вытекает из тождества параллелограмма).
- В ромб можно вписать прямоугольник, при этом его углы будут располагаться на серединах его сторон.
- Оси симметрии ромба обязательно будут перпендикулярны диагоналям ромба.
- Кроме прямоугольника в ромб можно вписать окружность. Ее центр будет совпадать с точкой, в которой пересекаются диагонали.
Зная вышеизложенные свойства, легко проводить вычисления величин, характеризующих данный ромб и строить внутри него геометрические фигуры.
Понятие периметра ромба
Периметр любой плоской геометрической фигуры составляет сумму длин его границ. Ромб не является исключением.
Исходя из определения, единицы измерения периметра аналогичны единицам длины.
Однако найти периметр ромба можно не только сложив длины всех четырех сторон. В геометрии существует еще один метод, который детально будет рассмотрен ниже.
Способы нахождения периметра
Через стороны
Поскольку у ромба все четыре стороны равны, его периметр можно выразить произведением длины одной стороны на 4.
P=4a
где P — периметр, a — длина стороны.
Нахождение периметра ромба можно проводить по еще одной формуле, используя длины диагоналей.
Через длину диагонали
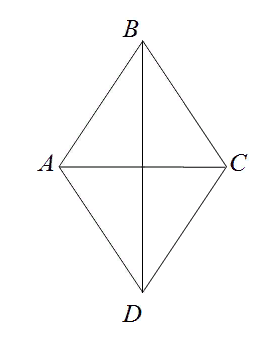
Рассмотрим рисунок.
Проведем в ромбе ABCD диагонали BD и AC. Они пересекаются в точке O под прямым углом и делятся этой точкой пополам. Можно записать равенства:
AO=OC=d1/2
BO=OD=d2/2
В результате деления ромба диагоналями на четыре треугольника, имеющих прямые углы, образовались геометрические фигуры AOB, AOD, BOC, DOC. Подробнее рассмотрим один треугольник — AOB.
Из рисунка видно, что сторона AB являясь стороной ромба, представляет собой гипотенузу в прямоугольнике. Далее воспользуемся известной теоремой Пифагора:
AB2=AO2+OB2
В эту формулу подставим величины длин катетов. Однако перед этим выразим их через ½ диагоналей.
AB2=(d1/2)2+(d2/2)2
Извлекая квадрат из этого выражения, получаем:
AB=√((d1/2)2+(d2/2)2)
В итоге находим периметр ромба:
Формулы для каждого способа
В ходе решения задач по теме «ромб» применяются следующие формулы:
- Для нахождения периметра:
Через длину стороны: P=4a
Используя длины диагоналей:
Кроме этого, на уроках по изучению характеристик ромба, рассматриваются формулы по нахождению его площади. Ее можно определить с помощью двух способов: через вычисление произведения высоты на длину стороны или половину произведения двух диагоналей.
Примеры решения задач
Задача 1
Длина стороны ромба составляет 10 см. Чему равен его периметр?
Решение.
Находить следует с использованием формулы: P=4a. Подставляем значение длины стороны и получаем P=40 см
Задача 2
Периметр ромба равен 36 см. Чему равна длина его стороны?
Решение.
Используется формула для нахождения периметра. Из нее вытекает действие для нахождения длины стороны: a=P/4
a=36/4=9 см
Задача 3
Дан ромб с длинами диагоналей 8 и 6 см. Чему равен его периметр?
Решение.
Используем способ нахождения периметра через квадрат из суммы квадратов половины диагоналей:
P=4*√((8/2)2+(6/2)2)=20см
Задача 4
Известно, что в ромбе одна из диагоналей равна 6 см, а один из углов равен 60о. Каков периметр этого ромба?
Решение.
Предположим, что длина диагонали AC составляет 6 см, а угол ABC составляет 60о
Обозначим длину стороны ромба (а по определению длины всех сторон равны) буквой a.
По основному свойству ромба о равенстве длин его сторон, треугольник ABC равнобедренный. В то же время, поскольку один из его углов равен 60о, он еще и равносторонний.
a=AC=6см
Теперь применяем формулу для нахождения периметра ромба через длину стороны:
PABCD=4*6=24 см