Приложения:
Ответы
Ответ:
20
Пошаговое объяснение:
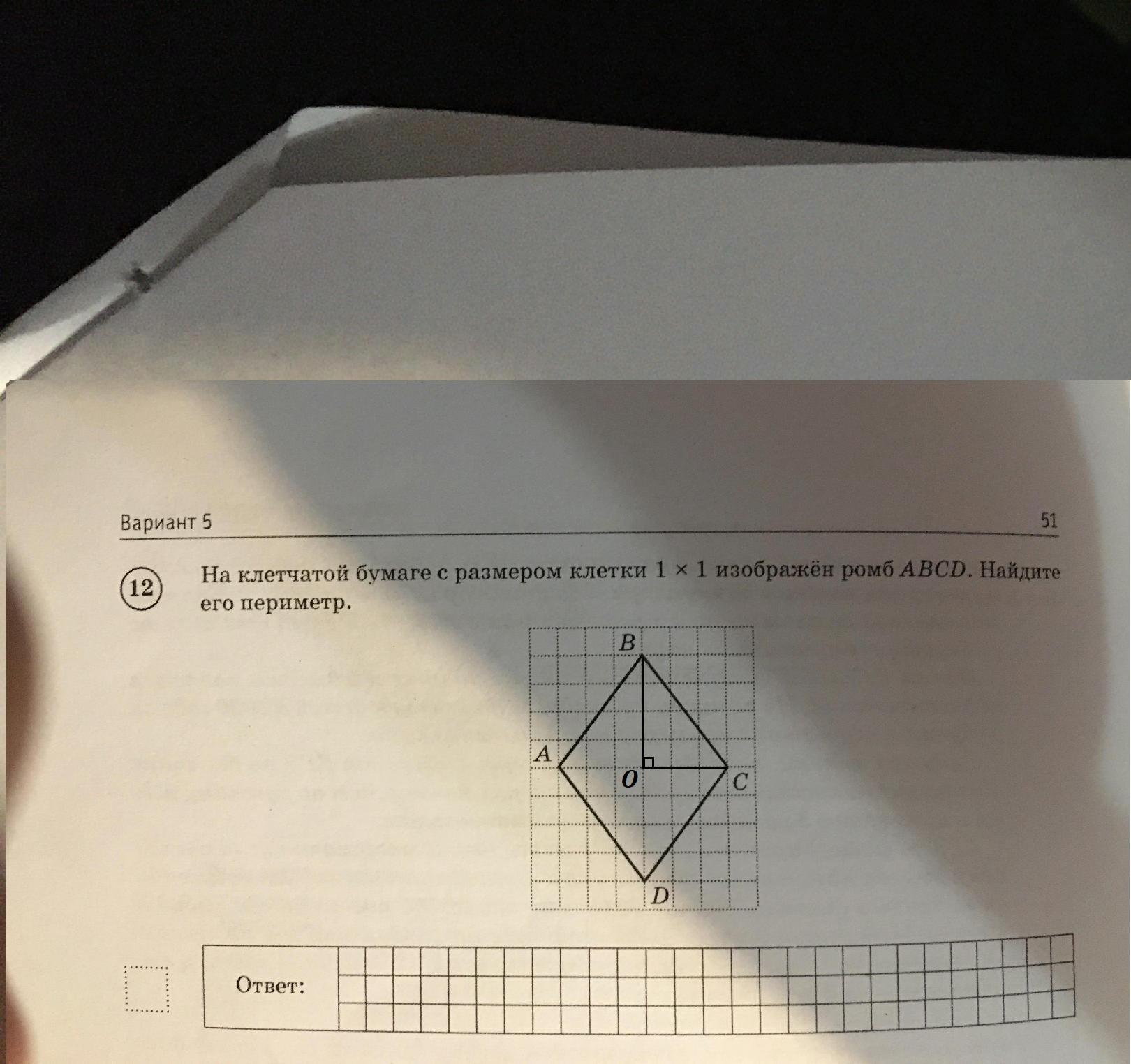
- Ромб – параллелограмм, у которого все стороны равны.
⇒ AB = BC = CD = AD
Внутри данного ромба построим прямоугольный ΔBOC, где BC – гипотенуза.
Так как 1 клетка = 1 ⇒ OC = 3 (так как 3 клетки) и BO = 4 (так как 4 клетки)
В ΔBOC:
Найдём BC по теореме Пифагора:
⇒ AB = BC = CD = AD = 5
- Периметр фигуры – сумма всех её сторон.
⇒
Или:
Так как в ромбе все стороны равны и этих сторон всего 4, то:
Приложения:
Интересные вопросы
Задания
Версия для печати и копирования в MS Word
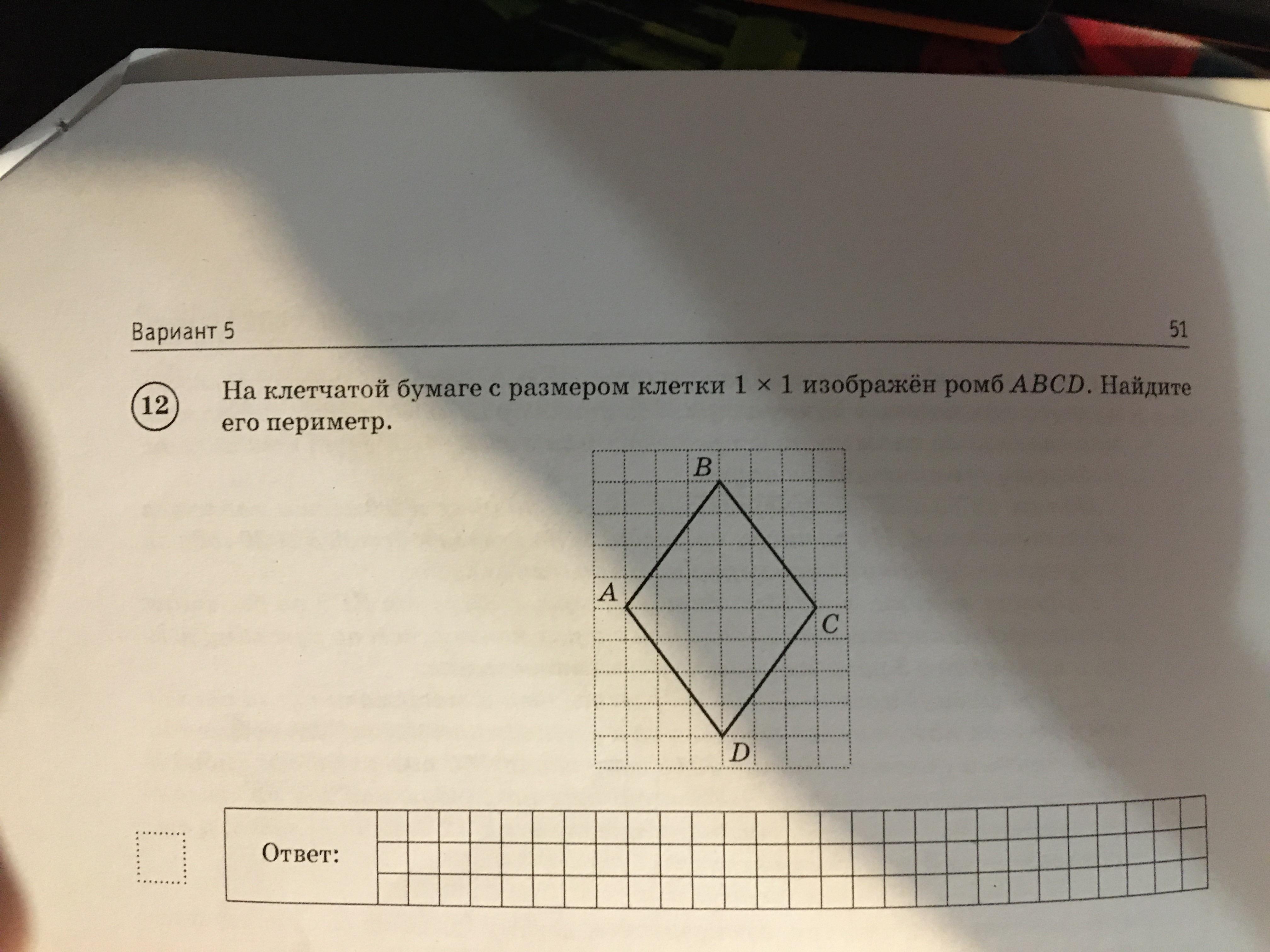
На клетчатой бумаге с размером клетки 1 × 1 изображён ромб ABCD. Найдите его периметр.
Спрятать решение
Решение.
Диагонали ромба пересекаются под углом 90° и точкой пересечения делятся пополам. Из рисунка видно, что диагонали AC и BD равны 8 и 6 соответственно. Из прямоугольного треугольника, катетами которого являются половины диагоналей ромба, а гипотенузой — сторона ромба, по теореме Пифагора найдём сторону ромба: Так как все стороны ромба равны, то периметр равен:
Ответ: 20.
Найдите периметр четырехугольника ABCD
27851. Найдите периметр четырехугольника ABCD, если стороны квадратных клеток равны √10.
Стороны ромба равны. Вычислим одну сторону и умножим её на 4. Сторона ромба является гипотенузой в прямоугольном треугольнике с катетами 1 и 3. Вычисляем:
Таким образом, периметр равен 40.
Проект “МатематикаЕГЭ” – Решение задач из открытого банка заданий ЕГЭ
Как найти периметр сторон четырехугольника, формула нахождения
Совсем недавно в России родители отправляли своих детей в первый класс и с нетерпением ждали их первых заданий. Они с удовольствием наблюдали за тем, как их дети знакомятся с буквами русского алфавита, учатся считать палочки и точечки, выводить различные кривые и прямые линии. Родители помогали знакомиться своим детям с тем, что тетрадь в клеточку предназначена для написания цифр, а тетрадь в линеечку — для письма.
Сегодня, будучи второклассниками, ученики России достигли больших успехов в сфере начального образования, а точнее, в математическом прогрессе. Учителя научили их складывать и вычитать, умножать, делить, измерять.
Кстати, по поводу измерения: с линейкой ребята вторых классов России уже знакомы, и применение ей, кроме как стрелять с задней парты в соседа бумажки, они тоже знают. Именно об измерениях мы и заведем сегодняшний разговор.
Как мы видим, прогресс обучения нынешних учеников проходит слегка в ускоренном режиме. С теми темами, например, такими как периметр, дети 90-х знакомились позже, а наши ребята узнают сегодня. Конечно, в этом нет ничего страшного. Время меняется, и программа обучения тоже должна не стоять на месте. Зато, как считают многие, наши дети будут умнее нас.
Школьное задание
Наверное, многих родителей сегодня удивляют нынешние задания для второклассников. В учебнике по математике для второго класса можно встретить такое задание, как, например: «Найди периметр четырехугольника, две стороны которого равны по 2 сантиметра, а другие две будут по 3 сантиметра». Как справиться с данным заданием?
Многие родители настоящего времени являются теми самыми детьми девяностых годов, и, естественно, в большинстве случаев, мало кто помнит, что такое периметр. Особенно, если учились не на отлично, да и не совсем на «хорошо».
Естественно, каждому родителю хотелось бы, чтоб его ребенку было проще в обучении, и они всеми силами стараются ему в этом помочь. Некоторым родителям сначала приходится справиться со своей душевной паникой, а уже потом продолжать объяснять своему ребенку. В этом случае многим помогает интернет, место, где можно найти ответы на все тревожные вопросы. Во времена девяностых, к сожалению, такой «роскоши» не было.
Вопросы:
- Что такое «периметр»?
- Как находить периметр четырехугольника?
Ответы на вопросы:
Для тех, кто знает, вспоминаем, а кто не знает — объясняем:
- Периметр — это сумма всех сторон четырехугольника. Всего лишь каждая грань по отдельности будет равна после сложения единому числу.
- Найти периметр, значит, что нужно взять линейку и измерить каждую границу четырехугольника. После выполнения данного действия необходимо сложить полученные числа между собой. Общая полученная сумма и будет являться периметром.
Решение:
В данном случае, по действиям нашей задачи, нам известны суммы сторон четырехугольника, а именно две из них по 2 сантиметра и две по 3 сантиметра. Поэтому нам остается всего лишь перечертить четырехугольник в тетрадь и сложить известные нам суммы каждой грани.
2+2+3+3=10
Как мы видим, периметр нашей четырехугольной фигуры равен 10.
В математике сумму всех сторон (периметр) мы обозначаем символом Р.
Теперь записываем правильное решение этой задачи:
Р=2+2+3+3;
Ответ: Р=10.
В математике существует формула, запомнив которую, вы никогда не будете забывать, как найти периметр (общую сумму всех сторон) четырехугольника и выглядит она так:
P = a + b + c + d (где a , b, c, d являются границами четырехугольника).
Кроме того, хотелось бы обратить внимание, что четырехугольник не обязательно будет являться прямоугольником. Это может быть и квадрат, у которого все стороны равны, и любая другая геометрическая фигура, у которой есть четыре стороны и такое же количество углов.
Грани произвольного четырехугольника могут совсем не совпадать ни с одной из сторон фигуры. Это могут быть совершенно разные числа. И, в итоге, получаются фигуры с четырьмя сторонами и теми же четырьмя углами. Фигура не будет похожа ни на квадрат, ни на прямоугольник, так как углы ее прямыми не будут. И периметр, соответственно мы вычисляем по той же самой единой формуле.
Или взять, например трапецию. Обычно у трапеции две стороны одинаковые, а другие две совсем не совпадают, но между собой параллельные.
На примере трапеция может выглядеть так: верхняя грань равна 2 сантиметра, левая и правая стороны по 3 сантиметра, соединяем их с нижней гранью и получаем трапецию. Высчитываем каждую ее сторону и снова получаем периметр четырехугольника.
Вычислить по формуле всегда будет проще, и не важно, каким числам равна каждая сторона.
Так как современные дети страны уже дошли до таблицы умножения, с периметром квадрата у них проблем не будет. Зная размер одной стороны квадрата, нужно умножить ее на все четыре равные стороны.
В общем, теперь стоит взять линейку с карандашом и лист бумаги. После этого следует начертить произвольные фигуры с четырьмя углами и высчитать общую сумму ее сторон.
Нахождение периметра ромба: формула и задачи
В данной публикации мы рассмотрим, каким образом можно посчитать периметр ромба и разберем примеры решения задач.
Формула вычисления периметра
1. По длине стороны
Периметр (P) ромба равняется сумме длин всех его сторон.
P = a + a + a + a
Т.к. все стороны данной геометрической фигуры равны, формулу можно представить в следующем виде (сторона умноженная на 4):
P = 4*a
2. По длине диагоналей
Диагонали любого ромба пересекаются под углом 90° и в точке пересечения делятся пополам, т.е.:
- AO=OC=d1/2
- BO=OD=d2/2
Диагонали делят ромб на 4 равных прямоугольных треугольника: AOB, AOD, BOC и DOC. Давайте подробнее остановимся на AOB.
Найти сторону AB, которая одновременно является гипотенузой прямоугольника и стороной ромба, можно, воспользовавшись теоремой Пифагора:
AB 2 = AO 2 + OB 2
Подставляем в эту формулу длины катетов, выраженные через половины диагоналей, и получаем:
Таким образом, периметр равняется:
Примеры задач
Задание 1
Найдите периметр ромба, если длина его стороны составляет 7 см.
Решение:
Используем первую формулу, подставив в нее известное значение: P = 4 * 7 см = 27 см.
Задание 2
Периметр ромба равен 44 см. Найдите сторону фигуры.
Решение:
Как мы знаем, P = 4*a. Следовательно, чтобы найти одну сторону (a), необходимо периметр разделить на четыре: a = P/4 = 44 см / 4 = 11 см.
Задание 3
Найдите периметр ромба, если известны его диагонали: 6 и 8 см.
Решение:
Воспользовавшись формулой, в которой задействованы длины диагоналей, получаем:
[spoiler title=”источники:”]
http://liveposts.ru/articles/education-articles/matematika/kak-najti-perimetr-storon-chetyrehugolnika-formula-nahozhdeniya
[/spoiler]
