Как найти периметр ромба в прямоугольнике.
vSyler
Пользователь
Регистрация:
29.08.2015
Сообщения: 151
Рейтинг: 53
Регистрация:
29.08.2015
Сообщения: 151
Рейтинг: 53
Есть прямоугольник, на сторонах которого расставлены точки. Если соединить 2 вершины прямоугольника и эти точки, то получится ромб. Как найти периметр ромба, если известны стороны прямоугольника?
peexthree
Пользователь
Регистрация:
15.09.2015
Сообщения: 202
Рейтинг: 74
Регистрация:
15.09.2015
Сообщения: 202
Рейтинг: 74
vSyler сказал(а):↑
Есть прямоугольник, на сторонах которого расставлены точки. Если соединить 2 вершины прямоугольника и эти точки, то получится ромб. Как найти периметр ромба, если известны стороны прямоугольника?
Нажмите, чтобы раскрыть…
ну смотри,если соединяем 2 вершины и точки прямугольника,то мы получаем пересечение 2х прямоугольников в прямоугольнике,высчитываешь эти 2 прямоугольника,получаешь пропорциональные стороны ромба.Далее просто.
2tangopls
Пользователь
Регистрация:
23.07.2014
Сообщения: 2602
Рейтинг: 1906
Регистрация:
23.07.2014
Сообщения: 2602
Рейтинг: 1906
vSyler сказал(а):↑
Есть прямоугольник, на сторонах которого расставлены точки. Если соединить 2 вершины прямоугольника и эти точки, то получится ромб. Как найти периметр ромба, если известны стороны прямоугольника?
Нажмите, чтобы раскрыть…
Точки произвольные? Дано соотношение разбитых сторон? если да, то по теореме пифагора найди 1 сторону
DEADLY9999
Пользователь
Регистрация:
25.06.2014
Сообщения: 903
Рейтинг: 327
Регистрация:
25.06.2014
Сообщения: 903
Рейтинг: 327
госпаде по пифагору вычисляешь гипотенузу, потом гипотенуза умножить на 4 т.к. ромб и изи
peexthree
Пользователь
Регистрация:
15.09.2015
Сообщения: 202
Рейтинг: 74
Регистрация:
15.09.2015
Сообщения: 202
Рейтинг: 74
ромб это Параллелограмм, все стороны к-рого равны,вот тебе еще помощь
vSyler
Пользователь
Регистрация:
29.08.2015
Сообщения: 151
Рейтинг: 53
Регистрация:
29.08.2015
Сообщения: 151
Рейтинг: 53
2tangopls сказал(а):↑
Точки произвольные? Дано соотношение разбитых сторон? если да, то по теореме пифагора найди 1 сторону
Нажмите, чтобы раскрыть…
Точки произвольные, соотношение разбитых сторон не дано.
yuokiex
Пользователь
Регистрация:
18.01.2015
Сообщения: 764
Рейтинг: 795
Регистрация:
18.01.2015
Сообщения: 764
Рейтинг: 795
vSyler
Пользователь
Регистрация:
29.08.2015
Сообщения: 151
Рейтинг: 53
Регистрация:
29.08.2015
Сообщения: 151
Рейтинг: 53
yuokiex сказал(а):↑
Нажмите, чтобы раскрыть…
2 вершины прямоугольника – вершины ромба. Но спасибо.
yuokiex
Пользователь
Регистрация:
18.01.2015
Сообщения: 764
Рейтинг: 795
Регистрация:
18.01.2015
Сообщения: 764
Рейтинг: 795
ecFulgrim
Пользователь
Регистрация:
02.08.2014
Сообщения: 821
Рейтинг: 644
Регистрация:
02.08.2014
Сообщения: 821
Рейтинг: 644
yuokiex сказал(а):↑
сори я туповат)
Нажмите, чтобы раскрыть…
Так то с твоим примером, он сам теперь сможет додумать, просто развернув ромб как ему надо и проделав практически идентичные операции.
vSyler
Пользователь
Регистрация:
29.08.2015
Сообщения: 151
Рейтинг: 53
Регистрация:
29.08.2015
Сообщения: 151
Рейтинг: 53
ecFulgrim сказал(а):↑
Так то с твоим примером, он сам теперь сможет додумать, просто развернув ромб как ему надо и проделав практически идентичные операции.
Нажмите, чтобы раскрыть…
Не совсем
Тема закрыта
-
Заголовок
Ответов Просмотров
Последнее сообщение
-
Сообщений: 7
19 May 2023 в 10:42Сообщений:7
Просмотров:22
-
Сообщений: 1
19 May 2023 в 10:03Сообщений:1
Просмотров:10
-
Сообщений: 7
19 May 2023 в 10:02Сообщений:7
Просмотров:30
-
Сообщений: 20
19 May 2023 в 09:53Сообщений:20
Просмотров:58
-
Сообщений: 16
19 May 2023 в 09:39Сообщений:16
Просмотров:36
В данной публикации мы рассмотрим, каким образом можно посчитать периметр ромба и разберем примеры решения задач.
- Формула вычисления периметра
- Примеры задач
Формула вычисления периметра
1. По длине стороны
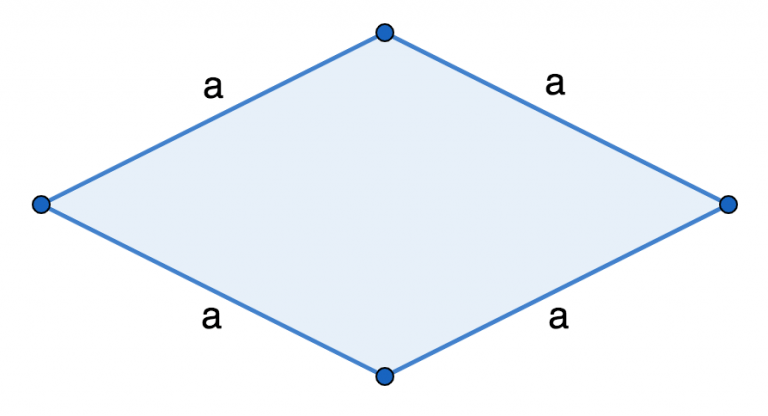
Периметр (P) ромба равняется сумме длин всех его сторон.
P = a + a + a + a
Т.к. все стороны данной геометрической фигуры равны, формулу можно представить в следующем виде (сторона умноженная на 4):
P = 4*a
2. По длине диагоналей
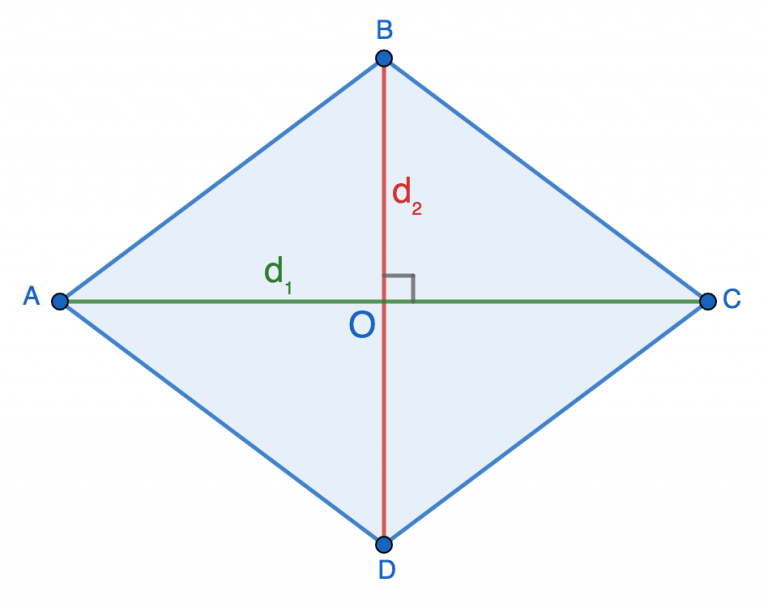
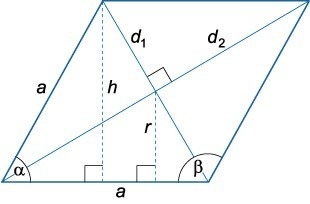
Диагонали любого ромба пересекаются под углом 90° и в точке пересечения делятся пополам, т.е.:
- AO=OC=d1/2
- BO=OD=d2/2
Диагонали делят ромб на 4 равных прямоугольных треугольника: AOB, AOD, BOC и DOC. Давайте подробнее остановимся на AOB.
Найти сторону AB, которая одновременно является гипотенузой прямоугольника и стороной ромба, можно, воспользовавшись теоремой Пифагора:
AB2 = AO2 + OB2
Подставляем в эту формулу длины катетов, выраженные через половины диагоналей, и получаем:
AB2 = (d1/2)2 + (d2/2)2, или
Таким образом, периметр равняется:
Примеры задач
Задание 1
Найдите периметр ромба, если длина его стороны составляет 7 см.
Решение:
Используем первую формулу, подставив в нее известное значение: P = 4 * 7 см = 27 см.
Задание 2
Периметр ромба равен 44 см. Найдите сторону фигуры.
Решение:
Как мы знаем, P = 4*a. Следовательно, чтобы найти одну сторону (a), необходимо периметр разделить на четыре: a = P/4 = 44 см / 4 = 11 см.
Задание 3
Найдите периметр ромба, если известны его диагонали: 6 и 8 см.
Решение:
Воспользовавшись формулой, в которой задействованы длины диагоналей, получаем:
В данной публикации мы рассмотрим, каким образом можно посчитать периметр ромба и разберем примеры решения задач.
1. По длине стороны
Периметр (P) ромба равняется сумме длин всех его сторон.
Т.к. все стороны данной геометрической фигуры равны, формулу можно представить в следующем виде (сторона умноженная на 4):
2. По длине диагоналей
Диагонали любого ромба пересекаются под углом 90° и в точке пересечения делятся пополам, т.е.:
Диагонали делят ромб на 4 равных прямоугольных треугольника: AOB, AOD, BOC и DOC. Давайте подробнее остановимся на AOB.
Найти сторону AB, которая одновременно является гипотенузой прямоугольника и стороной ромба, можно, воспользовавшись теоремой Пифагора:
Подставляем в эту формулу длины катетов, выраженные через половины диагоналей, и получаем:
Задание 1
Найдите периметр ромба, если длина его стороны составляет 7 см.
Решение:
Используем первую формулу, подставив в нее известное значение: P = 4 * 7 см = 27 см.
Задание 2
Периметр ромба равен 44 см. Найдите сторону фигуры.
Решение:
Как мы знаем, P = 4*a. Следовательно, чтобы найти одну сторону (a), необходимо периметр разделить на четыре: a = P/4 = 44 см / 4 = 11 см.
Задание 3
Найдите периметр ромба, если известны его диагонали: 6 и 8 см.
Решение:
Воспользовавшись формулой, в которой задействованы длины диагоналей, получаем:
Чтобы найти периметр ромба, необходимо длину его стороны умножить на четыре.
По определению ромб — это параллелограмм, у которого все стороны равны. Таким образом, формула для нахождения периметра ромба $ABCD$ со стороной $a$ имеет вид:
Задание. Найти периметр ромба $ABCD$ со стороной $a=2,5$ дм.
Решение. Для нахождения периметра ромба $ABCD$ воспользуемся формулой:
Ответ. $P_=10$ (дм)
Задание. Найти периметр ромба $ABCD$, если его диагонали равны соответственно $AC=6$ м и $BD=8$ м.
Решение. Сделаем рисунок.
Ответ. $P_=20$ (м)
Работы любой сложности
Квалифицированная помощь от опытных авторов
- Периметр ромба
- Способы нахождения
- По сторонам
- По двум диагоналям
- По диагонали и углу
- По площади и радиусу вписанной окружности
- По площади и синусу одного из углов
- Через большую диагональ и половинный угол
- Периметр ромба
- Способы нахождения
- По сторонам
- По двум диагоналям
- По диагонали и углу
- По площади и радиусу вписанной окружности
- По площади и синусу одного из углов
- Через большую диагональ и половинный угол
Периметр ромба
Ромб — это четырехугольник с равными сторонами.
Также его называют параллелограммом, у которого все ребра равны. При этом его противоположные углы тоже равны между собой. Если все углы равны 90 градусов, то это квадрат.
Периметр ромба — сумма длин всего его сторон или произведение любой его стороны на 4.
Способы нахождения
Рассмотрим все способы нахождения периметра этой фигуры.
По сторонам
Если нам известны величины одного из его ребер, мы без проблем можем найти P по формуле:
где a — это сторона ромба.
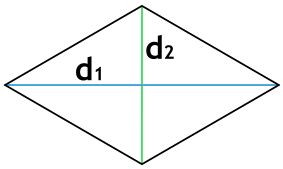
По двум диагоналям
Если наш ромб — не квадрат, то две его диагонали будут не равны между собой. Также в любом ромбе они пересекаются под углом 90 градусов, а в точке пересечения делятся пополам. Если обе из них нам известны, то можем вычислить периметр фигуры следующим образом:
где (d_1) и (d_2) — это диагонали четырехугольника.
Подобные вычисления получились исходя из свойств диагоналей равностороннего четырехугольника. Вместе со сторонами фигуры они образуют прямоугольный треугольник. По теореме Пифагора:
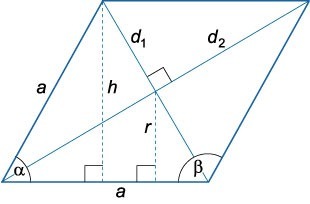
По диагонали и углу
Чтобы вычислить сумму всех ребер ромба данным способом, для начала нужно определить величину одной стороны:
- если нам известен острый угол α: (a=frac>;)
- если известен тупой угол (β: a=frac>.)
Далее расчет P будет выглядеть следующим образом:
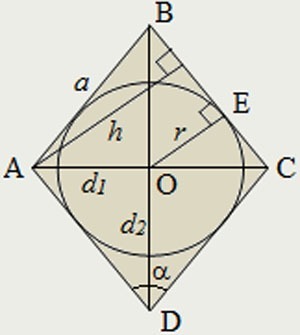
По площади и радиусу вписанной окружности
По известной площади и радиусу вписанной окружности можно находить P, опираясь на формулу:
где r — это радиус вписанной окружности.
По площади и синусу одного из углов
В этом случае формула расчета суммы всех сторон выглядит так:
Через большую диагональ и половинный угол
Получите помощь лучших авторов по вашей теме
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Ромб — это параллелограмм, у которого все стороны равны.
Формула периметра ромба ABCD , со сторонами: AB = CD = BC = AD = a
[ LARGE P_ = 4 cdot a ]
где:
P — периметр ромба
a — сторона ромба
Свойства ромба
- Диагонали ромба перпендикулярны;
- Диагонали ромба являются биссектрисами его углов.
Признаки ромба
- Параллелограмм, диагонали которого пересекаются под прямым углом, есть ромб;
- Параллелограмм, диагонали которого являются биссектрисами его углов, есть ромб.
Для нахождения периметра заданного ромба воспользуемся формулой
Подставляя значение a = 10 см, получим:
[ P_ = 4 cdot 10 = 40 text <см >]
Периметр ромба равен ( P_ ) = 40 см
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
- Математика
- Информатика
- Финансы
- Жизнь
- Здоровье
- Работа с текстом
- Работа с цветом
- Конвертеры
- Графики
- Алгебра
- Геометрия
- Тригонометрия
- Физика
- Химия
- Литература
- Информатика
- Астрономия
- Законы
- Единицы измерений
- Таблицы
- Инструкции
- Знаменитые химики
- Знаменитые физики
- Знаменитые математики
- Знаменитые биологи
- Знаменитые психологи
- Знаменитые философы
- ЕГЭ
- Гаджеты
- Разное
О сайте
На нашем сайте вы найдете множество полезных калькуляторов, конвертеров, таблиц, а также справочных материалов по основным дисциплинам.
Самый простой способ сделать расчеты в сети — это использовать подходящие онлайн инструменты. Воспользуйтесь поиском, чтобы найти подходящий инструмент на нашем сайте.
calcsbox.com
На сайте используется технология LaTeX.
Поэтому для корректного отображения формул и выражений
пожалуйста дождитесь полной загрузки страницы.
- Пользовательское соглашение
- Cookie
- О сайте
© 2021 Все калькуляторы online
Копирование материалов запрещено
Ромб представляет собой параллелограмм, у которого все стороны равны, а углы непрямые. Частным случаем ромба считается квадрат, однако классическая фигура должна иметь два острых и два тупых угла. Ромбические элементы иногда встречаются в реальной жизни, поэтому поиск периметра косоугольника может быть не только школьным заданием, но и житейской задачей.
Геометрия ромба
Ромб — это косоугольник с равными сторонами и равными высотами. Параллелограмм считается ромбом, если соблюдается хотя бы одно из перечисленных условий:
- диагонали фигуры пересекаются под прямым углом;
- диагонали одновременно являются биссектрисами углов;
- смежные стороны фигуры равны, а значит, равны все стороны четырехугольника.
Несколько ромбов с одинаковой длиной стороны могут выглядеть совершенно по-разному. Все дело в различной величине внутренних углов, соответственно, для определения угла фигуры недостаточно знать только длину ее стороны. Для этого необходимо измерить диагонали ромбовидной фигуры, так как они разбивают четырехугольник на 4 прямоугольных треугольника. Кроме того, ромб — симметричная фигура, поэтому его диагонали одновременно являются осями симметрии и биссектрисами для углов, из которых они выходят.
Ромб в реальной жизни
В трехмерной повседневности ромб встречается не слишком часто: наибольшее применение он находит в металлообработке, машиностроении, архитектуре, геральдике и дизайне. К примеру, ромбовидную форму имеют резцы металлообрабатывающих станков, нестандартные ромбические окна или геометрические узоры на коврах или стенных покрытиях. Наиболее очевидным примером ромба в реальности является тротуарная плитка, которая чаще всего выполняется именно в ромбовидной форме. Кроме того, форму ромба имеют отличительные знаки выпускников военных училищ и гражданских учебных заведений. Несмотря на довольно скудное распространение в реальном мире, вам может понадобиться вычислить периметр ромба для решения каких-либо практических задач.
Периметр ромбической фигуры
Периметр вычисляется как сумма длин всех сторон плоской геометрической фигуры. Ромб — четырехугольник с равными между собой сторонами, а значит, его периметр определяется простой формулой:
где a — длина одной стороны.
Если вам необходимо найти периметр ромбовидной фигуры для решения школьных заданий или практических задач, воспользуйтесь нашим онлайн-калькулятором. Для определения периметра наиболее простым способом вам понадобится измерить только сторону ромба, однако алгоритм калькулятора требует ввода двух переменных, поэтому в форму «Высота» введите 1. Также вы можете определить периметр, введя следующие сочетания переменных:
- две диагонали;
- диагональ и величина угла.
Примеры из реальной жизни
Рассмотрим пару примеров.
Пример №1
Определите периметр ромба, если длина его стороны равна 6 см. Если дана сторона, то это самый простой способ для определения периметра. Если вы помните простую формулу, то просто умножьте длину на 4. Если же нет, то наш калькулятор к вашим услугам. Введите значение в форму калькулятора, укажите высоту равную 1 и получите простой ответ:
В школьных заданиях определение периметра может усложняться.
Пример №2
Найдите периметр ромбической фигуры, если длина одной его диагонали равна 8 см, а величина острого угла составляет 60 градусов. Решая эту задачу вручную, вам бы понадобилось определять длину стороны, используя тригонометрические расчеты. Однако при помощи нашего сервиса вы можете просто ввести эти данные в форму калькулятора и получить готовый результат в виде:
Вы можете вычислить периметр ромбической фигуры, оперируя разными параметрами. Кроме того, калькулятор автоматически подсчитает все остальные атрибуты ромба, как острый и тупой угол, длины обеих диагоналей и длину стороны.
Заключение
Несмотря на то, что ромбовидные фигуры редко встречаются в реальности, у вас может возникнуть потребность определения периметра ромба, как для решения абстрактных школьных заданий, так и бытовых или производственных вопросов. Используя наш инструментарий, вы быстро и без ошибок вычислите все необходимые атрибуты любой геометрической фигуры.
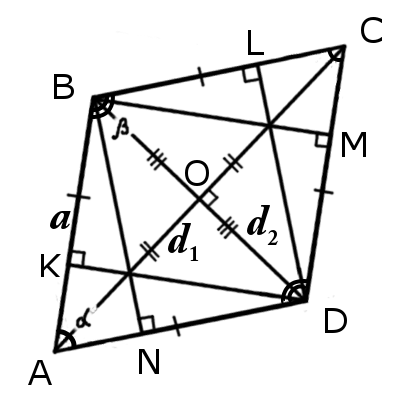
|
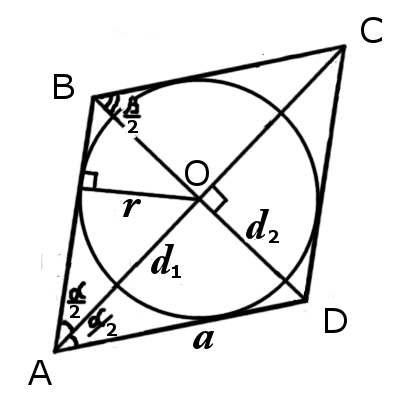 Рис.1 Рис.2 Рис.1 Рис.2
Признаки ромба∠BAC = ∠CAD или ∠BDA = ∠BDC Δ ABO = Δ BCO = Δ CDO = Δ ADO Основные свойства ромба∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC AC 2 + BD 2 = 4AB 2 Сторона ромбаФормулы определения длины стороны ромба:1. Формула стороны ромба через площадь и высоту:
|
Чтобы найти периметр ромба достаточно знать его сторону или диагонали и воспользоваться простейшей формулой. Чтобы облегчить эту задачу мы создали онлайн калькулятор, который мгновенно найдет периметр.
У нас вы также можете рассчитать периметр других четырехугольников: квадрата, прямоугольника, параллелограмма, трапеции.
Содержание:
- калькулятор периметра ромба
- формула периметра ромба через сторону
- формула периметра ромба через диагонали
- примеры задач
Ромб – параллелограмм, у которого все стороны равны.
Формула периметра ромба через сторону
{P = 4a}
a – сторона ромба
Формула периметра ромба через диагонали
{P = 2 sqrt{{d_1}^2+{d_2}^2}}
d1 и d2 – диагонали ромба
Примеры задач на нахождение периметра ромба
Задача 1
Найдите периметр ромба, если его диагонали равны 60см и 80см.
Решение
Для решения задачи используем вторую формулу.
P = 2 sqrt{{d_1}^2+{d_2}^2} = 2 sqrt{{60}^2+{80}^2} = 2 sqrt{3600+6400} = 2 sqrt{10000} = 2 cdot 100 = 200 : см
Ответ: 200 см
Проверим ответ на калькуляторе .
Задача 2
Найти периметр ромба, если его сторона равна 12см.
Решение
Воспользуемся первой формулой. Подставим в нее значение стороны ромба и вычислим его периметр:
P = 4a = 4 cdot 12 = 48 : см
Ответ: 48 см
Проверим ответ с использованием калькулятора .
Download Article
Download Article
A rhombus is a parallelogram with four congruent sides.[1]
These properties allow for numerous methods for finding the perimeter. Since all four sides of a rhombus are of equal length, finding the perimeter is possible when one side length is known. However, using geometry and trigonometry, it is also possible to find the perimeter even if you do not know the lengths of any sides of the rhombus.
-
1
Set up the formula for perimeter of a rhombus. Since, by definition, all four sides of a rhombus are the same length, the formula is
, where
equals the perimeter, and
equals the length of one side.[2]
- You could also use the formula
to find the perimeter, since the perimeter of any polygon is the sum of all its sides.[3]
- If you know that not all sides are the same length, then you are not working with a rhombus, and you cannot use this formula.
- If you don’t know the length of any side of the rhombus, you cannot use this method.
- A square is a special type of rhombus, with four 90-degree angles.
- You could also use the formula
-
2
Plug in the side length of the rhombus. Make sure you are substituting for the variable
.
- For example, if you know one side of the rhombus is 4 meters long, your formula will look like this:
.
Advertisement
- For example, if you know one side of the rhombus is 4 meters long, your formula will look like this:
-
3
Solve for
. To do this, multiply
by 4.
Advertisement
-
1
Notice that the two diagonals of your rhombus create four congruent triangles. Outline one of these triangles. You will use it to find the length of one side of the rhombus.
- Since the triangles are congruent, it doesn’t matter which one you outline.
-
2
Identify the 90 degree angle of your triangle. The two diagonals of a rhombus are perpendicular, so the central angle of your triangle will be 90 degrees. [4]
-
3
Label the hypotenuse of your triangle. The hypotenuse is the side opposite a 90 degree angle.[5]
Traditionally, the hypotenuse is labeled.
- The hypotenuse of your triangle is one side of the rhombus. So, if you find the length of
, you will know the length of one side of the rhombus.
- The hypotenuse of your triangle is one side of the rhombus. So, if you find the length of
-
4
Label the other two sides of your triangle. Traditionally, these are labeled
and
.
-
5
Find the length of side
. To do this, divide the length of the diagonal that
runs along by 2. Label the side length on your triangle.
-
6
Find the length of side
. To do this, divide the length of the diagonal that
runs along by 2. Label the side length on your triangle.
-
7
Set up the Pythagorean Theorem. The theorem states that
. This is a basic geometric formula for finding the side lengths of a right triangle.
-
8
Plug in the known side lengths of your triangle into the Pythagorean Theorem. Make sure you substitute for
and
, but the order doesn’t matter due to the commutative property.
-
9
-
10
-
11
Write your final answer. Don’t forget to include the correct unit of measurement.
- For example, a rhombus that has diagonals measuring 12 and 16 meters long has a perimeter of 40 meters.
Advertisement
-
1
Label the vertices of your rhombus, if they are not already labeled. It doesn’t matter which variables you give them.
-
2
Notice that the two diagonals of your rhombus create four congruent triangles. Outline one of these triangles. You will use it to find the length of one side of the rhombus.
- Since the triangles are congruent, it doesn’t matter which one you outline; however, for simplicity you should outline a triangle that shares a known angle of the rhombus.
- For example, I know that angle
of the rhombus is 70 degrees, so I would outline a triangle that includes point A.
-
3
Identify the 90 degree angle of your triangle. The two diagonals of a rhombus are perpendicular, so the central angle of your triangle will be 90 degrees. [7]
If this angle is not already labeled, label it.
-
4
-
5
Determine the measurement of the missing angle. Remember, the interior degrees of a triangle will add up to 180.[9]
So, if you know the measurement of two angles, you can subtract to find the measurement of the third angle. Label the degrees for this angle on your triangle. -
6
Determine the length of one side of your triangle. To do this, divide the length of the diagonal that the side runs along by 2. Label the side length on your triangle.
-
7
Set up a sine or cosine ratio. Whether you use sine or cosine will depend on which side and angle measurements of your triangle you know. For more information, read Use Right Angled Trigonometry.
- If you know the length of the side opposite to your angle, use sine. Set up the ratio
, where
is the measurement of the angle, “Opposite” is the length of the opposite side, and
is the length of the hypotenuse.
- If you know the length of the side adjacent to your angle, use cosine. Set up the ratio
. Where
is the measurement of the angle, “Adjacent” is the length of the adjacent side, and
is the length of the hypotenuse.
- For example, if you know that angle
of your triangle is 35 degrees, and the adjacent side is 8 centimeters, you should use cosine:
- If you know the length of the side opposite to your angle, use sine. Set up the ratio
-
8
Solve the ratio to find the length of the hypotenuse. The length of the hypotenuse is also the length of one side of your rhombus, so you need this measurement to find the perimeter of the rhombus.
-
9
-
10
Write your final answer. Your answer will be approximate since you rounded the sine or cosine measurement. Don’t forget to include the correct unit of measurement.
Advertisement
Add New Question
-
Question
What is the perimeter and area of a rhombus with diagonals of 24 cm and 7 cm?
To find the perimeter, follow the steps described in method 2, where you use the lengths of the diagonals to set up the Pythagorean Theorem.
1/2 of 24 = 12; 1/2 of 7 = 3.5.
So:
12^2 + 3.5^2 = c^2
144 + 12.25 = c^2
156.25 = c^2
12.5 = c, or the length of one side of the rhombus (S)
P = 4S
P = 4(12.5)
P= 50 cmTo find the area, you can read the article “Calculate the Area of a Rhombus.” (http://www.wikihow.com/Calculate-the-Area-of-a-Rhombus)
-
Question
What if the sides are not equal?
If the sides of the shape are not equal, then the figure is not a rhombus. You can still find the perimeter of any shape by adding up the length of all its sides.
-
Question
How do I find the perimeter of a rhombus whose area is 60 cm2 and has a diagonal of 15 cm?
The area (60) is half the product of the diagonals. If d is the unknown diagonal, then 60 = 15d / 2. So 15d = 120, and d = 8 cm. The diagonals of a rhombus are perpendicular to and bisect each other, forming four right triangles, each with legs of 7.5 cm and 4 cm (half each diagonal). By the Pythagorean theorem, we find that each of the sides of the rhombus is √([7.5)² + (4)²] = √[56.25 + 16] = √72.25 = 8.5 cm. The perimeter of the rhombus is four times the length of one side: 34 cm.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
You can add up the lengths of the sides to get the perimeter of any polygon – a triangle, rectangle, pentagon, or other straight-sided shape. Circles and other curved shapes require different formulas.
Thanks for submitting a tip for review!
Advertisement
References
About This Article
Article SummaryX
To find the perimeter of a rhombus when you have the length of one of the sides, multiply that length by 4. This works because all 4 sides of a rhombus are equal length. Keep reading to learn how to use the Pythagorean Theorem to find the perimeter of a rhombus when you know the diagonal!
Did this summary help you?
Thanks to all authors for creating a page that has been read 102,439 times.