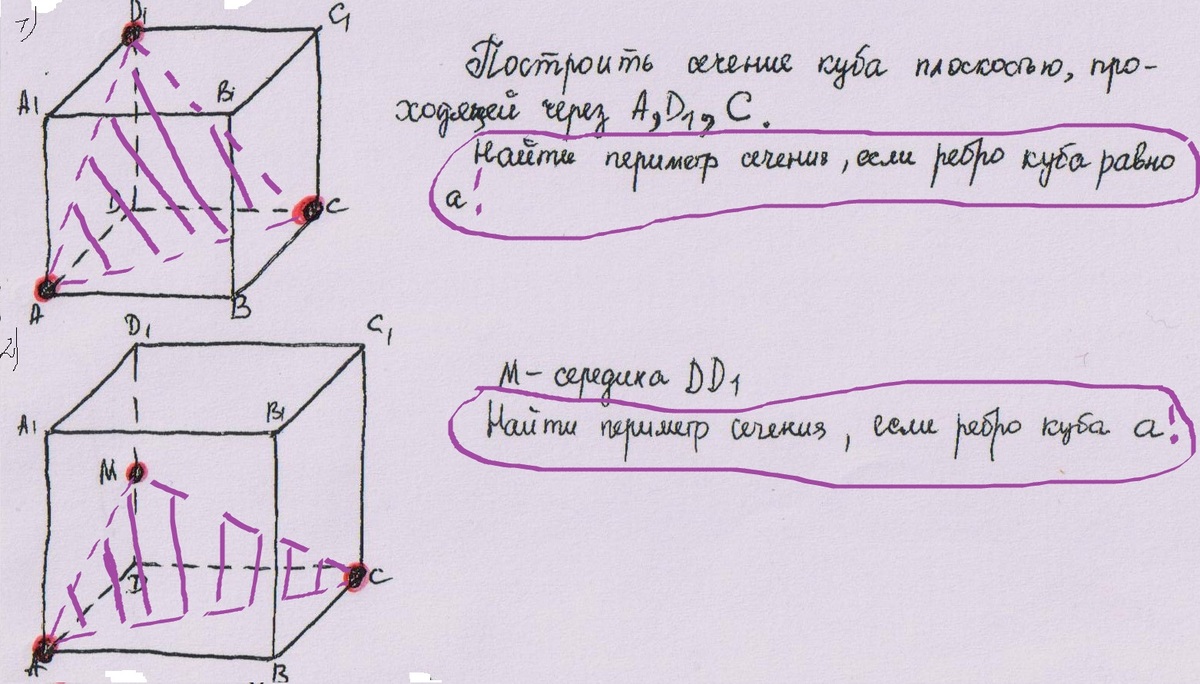
Найти периметры сечений, если ребро куба равно а.

Вы зашли на страницу вопроса Найти периметры сечений, если ребро куба равно а?, который относится к
категории Геометрия. По уровню сложности вопрос соответствует учебной
программе для учащихся 10 – 11 классов. В этой же категории вы найдете ответ
и на другие, похожие вопросы по теме, найти который можно с помощью
автоматической системы «умный поиск». Интересную информацию можно найти в
комментариях-ответах пользователей, с которыми есть обратная связь для
обсуждения темы. Если предложенные варианты ответов не удовлетворяют,
создайте свой вариант запроса в верхней строке.
Светило науки – 7292 ответа – 165986 раз оказано помощи
Через две точки можно провести прямую, если эти точки лежат в одной плоскости.
Здесь А и Д лежат в одной плоскости, поэтому
через них можно провести прямую.
Соединим их.
А и М тоже лежат в одной плоскости, соединим их.
Плоскость (BCC₁) параллельна плоскости (ADD₁),поэтому через М проводим прямую параллельно DD1.
Она пересеклась с СС1. Обозначим точку их пересечения К.
Точки
К и D₁ лежат в одной плоскости
, ⇒ через них можно провести прямую, лежащую в этой плоскости.
Получено нужное сечение АМКD₁.
Для того, чтобы вычислить периметр сечения, нужно найти длину всех стороны четырехугольника АМКD₁
АD₁ – диагональ квадрата
со стороной 4
АD₁=4√2
МК параллельна ВС₁=AD₁ и является средней линией треугольника ВСС₁.
Она равна половине ВС₁
МК=2√2
⊿АВМ=⊿КС₁D₁ по двум сторонам и углу между ними.
АМ=КD₁
Из треугольника АВМ
, где АВ=4, ВА=2
АМ=√(АВ²+ВМ²)=√(16+4)=2√5
Периметр АМКD₁
Р=2*2√5+4√2+2√2Р=6√2+4√5 (единиц длины)
———-
bzs@

как найти периметр куба
Наша Группа
Знаток
(466),
закрыт
4 года назад
Дре
Знаток
(355)
9 лет назад
Чтобы найти периметр куба, определите длину одного из его ребер и умножьте это число на 12. В виде формулы это правило можно записать следующим образом: P = 12 * a,где: Р – периметр куба, а – длина его стороны. Подобная формула может понадобиться если нужно собрать каркас куба, равного существующему.
14 января 2023 21:44
288
Найти периметры сечений, если ребро куба равно а.
Посмотреть ответы
1)AD1=D1C=AC
найти:P(ad1c)=AD1+D1C+AC=3AC=?
Рассмотрим ADC: – прямоугольный треугольник
AC^2=AD^2+DC^2
AC^2=2a^2
AC=a*√2
P=3*a*√2
2)MD=a/2
найти:P(amc)=AM+MC+AC
Рассмотрим AMD: – прямоугольный треугольник
AM^2=AD^2+MD^2
AM^2=a^2+a^2/4=5a^2/4
AM=a*√5 :2
AM=MC
AC=a*√2 – это мы получили из первой задачи.
P(amc)=AM+MC+AC=2*(a*√5 :2)+a*√2 =a*√5+a*√2
Еще вопросы по категории Геометрия
Это пример построения с использованием параллельности прямых.
Дело в том, что в данном случае точка и ребро лежат в параллельных плоскостях. Поэтому и линия пересечения плоскости сечения с гранью, в которой лежит точка, дожна быть параллельна ребру, через которое сечение проходит. А ребро параллельно одной из сторон грани.
Скажем, если мы выбрали ребро основания, пусть ближнее к нам, и центр дальней от нас боковой грани, то по той боковой грани пройдет в сечении прямая, параллельная основанию, то есть “нижнему” ребру боковой грани. Теперь полностью ясно, как строить сечение – в плоскости боковой грани через центр проводим прямую, параллельную основанию (такую “горизонтальную среднюю линюю”) и середины сторон, которые она пересечет, соединяем с концами того ребра основания, через которое мы сечем… то есть просто в плоскостях боковых граней замыкаем фигуру сечения. Это будет прямоугольник со сторонами а и а*корень(5)/2. Периметр а*(2 + корень(5)).