Сечения трехмерных фигур — площади и периметр
Умеешь строить сечения трехмерных фигур – точно не пропадешь.
В этой статье я расскажу тебе об алгоритме построения сечений и разберу пример!
Поехали!
Алгоритм определения площади и периметра сечения объемных фигур
- Нарисовать сечение.
- Определить фигуру, которая получилась в этом сечении.
- Вспомнить формулы площади/периметра этой фигуры.
- Найти площадь/периметр фигуры.
Стандартное сечение имеет вид треугольника, круга или четырехугольника. Следовательно, нам необходимо искать площади именно этих фигур.
Площадь сечения
Площадь треугольника
![]()
![]()
Площадь круга
![]()
![]()
Площадь прямоугольника
![]()
![]()
Пример решения задачи
![]()
Диаметр основания конуса ( displaystyle left( AB right)) равен ( displaystyle 8) см.
Длина образующей ( displaystyle left( AC; BC right)) равна ( displaystyle 5) см (линия от вершины конуса до любой точки его основания).
Найдите площадь осевого сечения этого конуса.
Осевое сечение конуса – это равнобедренный треугольник ( displaystyle left( ABC right)), высота которого совпадает с высотой конуса ( displaystyle left( CO right)), а основание ( displaystyle left( AB right)) является диаметром основания конуса.
Значит, ( displaystyle S) осевого сечения конуса =( displaystyle S) треугольника ( displaystyle ABC).
Вспомним формулу площади треугольника:
| ( displaystyle S=frac{(COcdot AB)}{2} ) | begin{matrix} AB -длина стороны треугольника \ CO – высота, опущенная на сторону AB \ end{matrix} |
Найдем высоту ( displaystyle Delta ABC):
Рассмотрим ( displaystyle Delta COA).
т.к. ( displaystyle OC) – высота ( displaystyle Delta ABC rightarrow angle COA=90{}^circ rightarrow Delta COA) – прямоугольный.
( displaystyle AO=frac{AB}{2}=frac{8}{2}=4) (т.к. ( displaystyle AO) – радиус окружности, ( displaystyle AB) – диаметр).
Найдем ( displaystyle AC):
По теореме Пифагора:
( displaystyle A{{C}^{2}}=C{{O}^{2}}+A{{O}^{2}}; C{{O}^{2}}=A{{C}^{2}}-A{{O}^{2}}={{5}^{2}}-{{4}^{2}}=9см; CO=sqrt{9}=3см)
Подставим получившиеся значения в формулу площади:
( displaystyle {{S}_{ABC}}=frac{left( COcdot AB right)}{2}=frac{3cdot 8}{2}=)( displaystyle 12см{{ }^{2}})
Площадь осевого сечения этого конуса равна ( displaystyle 12см{{ }^{2}}).
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
![]()
Алексей Шевчук — ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 — WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org — email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж — c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
- отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».
Ответ:
10 ед.
Объяснение:
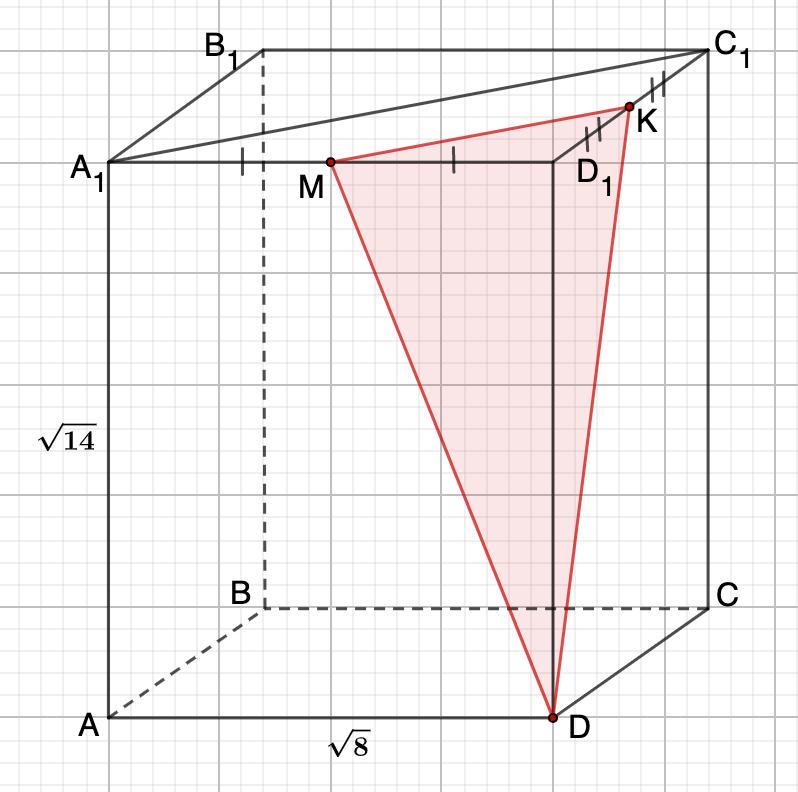
Дано: Правильная призма ABCDA₁B₁C₁D₁;
A₁M=MD₁; D₁K=KC₁;
AA₁=√14; AD=√8
Найти: Рс – периметр сечения.
Решение:
Призма правильная ⇒ в основании квадрат.
1) Рассмотрим ΔA₁C₁D₁ – прямоугольный, равнобедренный.
A₁M=MD₁; D₁K=KC₁ (условие)
⇒ МК – средняя линия
МК=А₁С₁:2=4:2=2 (средняя линия равна половине основания)
2) Рассмотрим ΔMDD₁ – прямоугольный.
По теореме Пифагора:
Аналогично
3) Найдем периметр сечения.
Периметр – сумма длин всех сторон треугольника.
(ед)
Приложения:
Онлайн-урок: Каждое ребро тетраэдра DABC равно 2 см. Постройте сечение тетраэдра плоскостью, проходящей через точки В, С и середину ребра AD. Вычислите периметр сечения.
Дано:
DАВС – тетраэдр
Все ребра 2 см
Найти:
1) Сечение через В и С и середину ребра АD
2) P – ?
Решение:
Согласно условию задачи, выполним чертеж (Рис.1):
Рис.1
1) Так как по условию все ребра равны, то перед нами правильный тетраэдр.
Обозначим точкой Е середину ребра АD. Проведем высоту АК, которая является также медианой в треугольнике АВС.
Соединим точки В, С и Е. Треугольник ЕВС – искомое сечение.
2) Периметр сечения равен:
Р = ВС + ЕВ + СЕ
Где ВС = 2 см по условию задачи
Треугольники АЕС и АЕВ равны между собой по двум сторонам и углу между ними, так как:
АВ = АС по условию
АЕ – общая сторона
∠ЕАС = ∠ЕАВ = 60 º так как по условию АВ = АС = ВС
Тогда, из равенства треугольников следует:
ЕС = ЕВ
Треугольник ЕВС – равнобедренный, где ЕК – высота, медиана и биссектриса.
Угол КАВ = 0,5 · САВ = 0,5 · 60 = 30º
Найдем АК:
Треугольник АЕК является прямоугольным, согласно теореме о трех перпендикулярах, где ∠АЕК = 90º
Тогда, по тереме Пифагора:
Тогда периметр равен:
The cross section of a solid is a plane section resulting
from a cut (real or imaginary) perpendicular to the length (or breadth of
height) of the solid.
If the shape and size of the cross section is the same at
every point along the length (or breadth or height) of the solid then the cross
section is uniform.
|
|
|
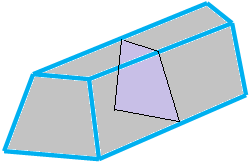
The two solids shown above have uniform cross sections.
The figure given below is a solid (Cone) whose cross sections perpendicular to height are not uniform.
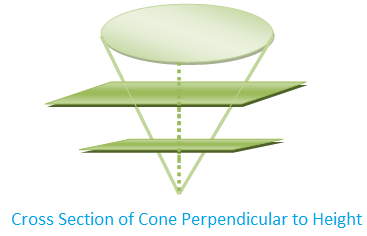
Volume of a solid figure with uniform cross section
= (Area of the cross section) × length (or height or breadth)
= A × h
Lateral surface area of a solid figure with uniform cross section
= (Perimeter of the cross section) × length (or height or breadth)
= P × h
Total surface area of a solid figure with uniform cross section
= Lateral surface area + Sum of the areas of the two plane ends
= P × h + 2 × A
9th Grade Math
From Cross Section to HOME PAGE
Didn’t find what you were looking for? Or want to know more information
about Math Only Math.
Use this Google Search to find what you need.

Дано: А…D1 – куб. Sполн=12. Найти: периметр сечения куба плоскостью, проходящей через вершины А1, С1 и D

Комментарии

Sполн=12=>S(1 кв) =12:6=2=> сторона квадрата √2

Длина одной диагонали квадрата по т Пифагора 2. Диагонали равных квадратов равны=> в сечении равносторонний треугольник. Площадь равностороннего треугольника равна (а^2√3)/4 .



Светило науки – 481 ответ – 0 раз оказано помощи
Смотрите фото. Sграни=12/6=2 ед. изм.² => А1В1=√2 ед. изм. => по т. Пифагора А1С1=√2*А1В1²=√2*2=√4=2 ед. изм. Т. к. А1С1=DC1=A1D => Pсеч=3*А1С1=3*2=6 ед. изм.
Ответ: 6 ед. изм.