Как найти периметр сечения правильной треугольной призмы

Как найти периметр сечения правильной треугольной призмы

vevexa122

vevexa122

Вопрос по геометрии:

каждое ребро треугольной призмы равна а. Найдите периметр сечения призмы плоскостью основания и противоположную вершину верхного основания.

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!

Ответы и объяснения 1

grorisifo643

grorisifo643

Правильное условие:

Каждое ребро треугольной призмы равна а. Найдите периметр сечения призмы плоскостью проходящей через сторону основания и противоположную вершину верхнего основания.

Изображение к ответу

Знаете ответ? Поделитесь им!

Гость

Гость ?

Как написать хороший ответ?

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

  • Отвечать достоверно на те вопросы, на которые знаете
    правильный ответ;
  • Писать подробно, чтобы ответ был исчерпывающий и не
    побуждал на дополнительные вопросы к нему;
  • Писать без грамматических, орфографических и
    пунктуационных ошибок.

Этого делать не стоит:

  • Копировать ответы со сторонних ресурсов. Хорошо ценятся
    уникальные и личные объяснения;
  • Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
    знаю» и так далее;
  • Использовать мат – это неуважительно по отношению к
    пользователям;
  • Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Источник

Вы можете увидеть призмы как на уроке математики, так и на протяжении всей вашей повседневной жизни. Кирпич – это прямоугольная призма. Упаковка апельсинового сока – это тип призмы. Коробка из ткани представляет собой прямоугольную призму. Амбары представляют собой тип пятиугольной призмы. Пентагон – это пятиугольная призма. Аквариум представляет собой прямоугольную призму. Этот список можно продолжать и продолжать.

Призмы по определению – это сплошные объекты с одинаковыми концевыми формами, одинаковыми сечениями и плоскими боковыми гранями (без кривых) И хотя большинство математических задач и примеров из реальной жизни, касающихся вычислений призмы, связаны с формулой объема или формулой площади поверхности, прежде чем вы сможете это сделать, вам нужно сначала понять один расчет: периметр призмы.

Что такое призма?

Общее определение призмы – это трехмерная сплошная форма, которая имеет следующие характеристики:

  • Это многогранник (то есть это сплошная фигура).
  • Поперечное сечение объекта является одинаковым по всей длине объекта.
  • Это параллелограмм (четырехсторонняя форма, в которой противоположные стороны параллельны друг другу).
  • Грани объекта плоские (без изогнутых граней).
  • Две концевые формы идентичны.

Название призмы происходит от формы двух концов, которые известны как основания. Это может быть любая форма (кроме кривых или кругов). Например, призма с треугольными основаниями называется треугольной призмой. Призма с прямоугольными основаниями называется прямоугольной призмой. Этот список можно продолжить.

Рассматривая характеристики призм, это исключает сферы, цилиндры и конусы как призмы, потому что они имеют изогнутые грани. Это также устраняет пирамиды, потому что они не имеют одинаковых основных форм или идентичных поперечных сечений повсюду.

Периметр призмы

Говоря о периметре призмы, вы на самом деле имеете в виду периметр базовой формы. Периметр основания призмы такой же, как периметр вдоль любого поперечного сечения призмы, поскольку все поперечные сечения одинаковы по всей длине призмы.

Периметр измеряет сумму длин любого многоугольника. Таким образом, для каждого типа призмы вы найдете сумму длин любой формы, являющейся основанием, и это будет периметр призмы.

Например, формула для нахождения периметра треугольной призмы будет суммой трех длин треугольника, составляющего основание, или:

Периметр треугольника = a + b + c, где a , b и c – три длины треугольника.

Это будет периметр формулы прямоугольной призмы:

Периметр прямоугольника: 2l + 2w, где l – длина прямоугольника, а w – ширина.

Примените стандартные расчеты периметра к базовой форме призмы, и это даст вам периметр.

Зачем вам нужно рассчитывать периметр призмы?

Поиск периметра призмы не кажется слишком сложным, если вы понимаете, о чем идет речь. Однако периметр является важным расчетом, который учитывает формулы площади и объема поверхности для некоторых призм.

Например, это формула для определения площади поверхности правой призмы (правая призма имеет идентичные основания и стороны, которые все прямоугольные):

Площадь поверхности = 2b + ph

где b равно площади основания, p равно периметру основания, а h равно высоте призмы. Вы можете видеть этот периметр, необходимый для определения площади поверхности.

Пример задачи: периметр прямоугольной призмы

Допустим, у вас есть проблема с правильной прямоугольной призмой, и вас попросили найти периметр. Вам даны следующие значения:

Длина = 75 см

Ширина = 10 см

Высота = 5 см

Чтобы найти периметр, используйте формулу для нахождения периметра прямоугольной призмы, поскольку имя говорит о том, что основание представляет собой прямоугольник:

Периметр = 2l + 2w = 2 (75 см) + 2 (10 см) = 150 см + 20 см = 170 см

Затем вы можете продолжить, чтобы найти площадь поверхности, потому что у вас есть высота, у вас есть периметр основания, и это считается, что эта призма является правой призмой.

Площадь основания равна длине × ширине (как всегда для прямоугольника), которая равна:

Площадь основания = 75 см × 10 см = 750 см 2

Теперь у вас есть все значения для расчета площади поверхности:

Площадь поверхности = 2b + ph = 2 (750 см 2) + 170 см (5 см) = 1500 см 2 + 850 см = 2350 см 2

Источник

Всего: 10    1–10

Добавить в вариант

Треугольная пирамида ABCD пересекается с плоскостью P по четырехугольнику EFGH так, что вершины E и F лежат на ребрах AB и AC и длина отрезка EF равна 1. Известно, что плоскость P параллельна противоположным ребрам AD и BC, которые равны соответственно 4 и 2. Найти периметр четырехугольника.

В основании правильной треугольной призмы ABCA1B1C1 лежит треугольник со стороной 6. Высота призмы равна 4. Точка N  — середина ребра A1C1.

а)  Постройте сечение призмы плоскостью BAN.

б)  Найдите периметр этого сечения.

В основании правильной треугольной призмы ABCA1B1C1лежит треугольник со стороной 8. Высота призмы равна 3. Точка N  — середина ребра A1C1.

а)  Постройте сечение призмы плоскостью BAN.

б)  Найдите площадь этого сечения.

Основанием прямой четырехугольной призмы ABCDA’B’C’D’ является квадрат ABCD со стороной 3 корень из: начало аргумента: 2 конец аргумента , высота призмы равна 2 корень из: начало аргумента: 7 конец аргумента . Точка K  — середина ребра BB’. Через точки K и С’ проведена плоскость α, параллельная прямой BD’.

а)  Докажите, что сечение призмы плоскостью α является равнобедренным треугольником.

б)  Найдите периметр треугольника, являющегося сечением призмы плоскостью α.

В основании правильной треугольной призмы ABCA1B1C1лежит треугольник со стороной 6. Высота призмы равна 4. Точка N  — середина ребра A1C1.

а)  Постройте сечение призмы плоскостью BAN.

б)  Найдите периметр этого сечения.

Основанием прямой четырёхугольной призмы ABCDA1B1C1D1 является квадрат ABCD со стороной 5 корень из 2 , высота призмы равна 2 корень из 1 4. Точка K  — середина ребра BB1. Через точки K и C1 проведена плоскость α параллельная прямой BD1.

а)  Докажите, что сечение призмы плоскостью α является равнобедренным треугольник.

б)  Найдите периметр треугольника, являющегося сечением призмы плоскостью α.

В правильной треугольной пирамиде SABC сторона основания AB равна 6, а боковое ребро SA равно 4. Точки M и N  — середины рёбер SA и SB соответственно. Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды.

а)  Докажите, что плоскость α делит медиану CE основания в отношении 5 : 1, считая от точки C.

б)  Найдите периметр многоугольника, являющегося сечением пирамиды SABC плоскостью α.

ABCA1B1C1  — правильная призма, сторона AB равна 16. Через точки M и P, лежащие на рёбрах AC и BB1 соответственно, проведена плоскость α, параллельная прямой AB. Сечение призмы этой плоскостью  — четырёхугольник, одна сторона которого равна 16, а три другие равны между собой.

а)  Докажите что периметр сечения призмы плоскостью α больше 40.

б)  Найдите расстояние от точки A до плоскости α, если упомянутый периметр равен 46.

ABCA1B1C1  — правильная призма, сторона AB равна 25. Через точки M и P, лежащие на рёбрах AC и BB1 соответственно, проведена плоскость α, параллельная прямой AB. Сечение призмы этой плоскостью  — четырёхугольник, одна сторона которого равна 25, а три другие равны между собой.

а)  Докажите что периметр сечения призмы плоскостью α больше 62,5.

б)  Найдите расстояние от точки A до плоскости α, если упомянутый периметр равен 64.

Всего: 10    1–10

Источник

Ответ:

10 ед.

Объяснение:

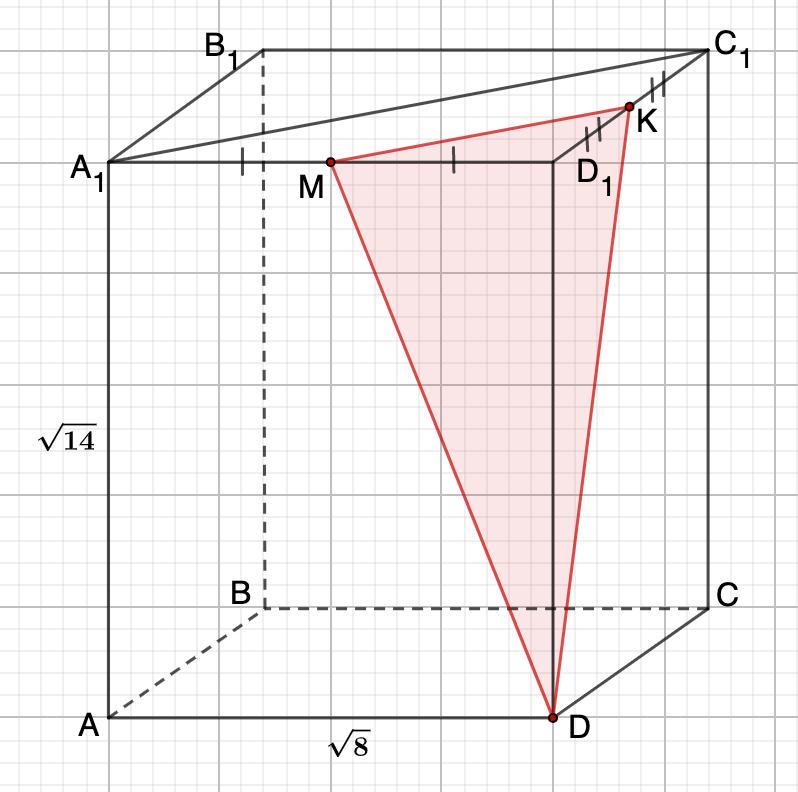
Дано: Правильная призма ABCDA₁B₁C₁D₁;

A₁M=MD₁; D₁K=KC₁;

AA₁=√14; AD=√8

Найти: Рс – периметр сечения.

Решение:

Призма правильная ⇒ в основании квадрат.

1) Рассмотрим ΔA₁C₁D₁ – прямоугольный, равнобедренный.

A_1C_1=sqrt{A_1D_1^2+D_1C_1^2}=sqrt{8+8}=4

A₁M=MD₁; D₁K=KC₁ (условие)

⇒ МК – средняя линия

МК=А₁С₁:2=4:2=2 (средняя линия равна половине основания)

2) Рассмотрим ΔMDD₁ – прямоугольный.

displaystyle MD_1=frac{sqrt{8} }{2}=frac{2sqrt{2} }{2}=sqrt{2}

По теореме Пифагора:

displaystyle MD=sqrt{MD_1^2+D_1D^2}=sqrt{2+14}=4

Аналогично

displaystyle DK=4

3) Найдем периметр сечения.

Периметр – сумма длин всех сторон треугольника.

displaystyle P_{DMK}=2+4+4=10 (ед)

Приложения:

Источник


  •
  • 0




Высота правильной треугольной призмы АВСА1В1С1 = 3, а сторона основания = 8. Найти периметр сечения, проходящего через вершину А и середины рёбер А1В1 и А1С1

  • Комментариев (0)



  • 0


1. Рассмотрим треугольник АА1М. Он прямоугольный (по условию). Найдём АМ по теореме Пифагора:
АМ²=АА1²+А1М²
АМ²=3²+4²
АМ²=25
АМ=5
2. Треугольники АА1М и АА1N равны как прямоугольные по двум катетам (А1М=А1N по условию, АА1 — общая). Тогда АМ=AN=5.
3. Рассмотрим треугольники С1А1В1 и МАN. Они подобны по двум сторонам и общему углу С1А1В1 — А1M:A1C1=A1N:A1B1=1:2. Тогда MN=½C1B1=8:2=4.
P AMN=AM+AN+MN=5+5+4=14
Ответ: 14.

RE: Высота правильной треугольной призмы АВСА1В1С1 = 3, а сторона основания = 8. Найти периметр сече...

  • Комментариев (0)

Источник

Добавить комментарий