Периметр кругового сектора Калькулятор
| Search | ||
| Дом | математика ↺ | |
| математика | Геометрия ↺ | |
| Геометрия | 2D геометрия ↺ | |
| 2D геометрия | Круг ↺ | |
| Круг | Круговой сектор ↺ | |
| Круговой сектор | Периметр кругового сектора ↺ |
|
✖Угол кругового сектора — это угол между радиальными ребрами кругового сектора или центральный угол, в котором круг разрезается, образуя круговой сектор.ⓘ Угол кругового сектора [∠Sector] |
+10% -10% |
||
|
✖Радиус кругового сектора — это радиус круга, из которого образован круговой сектор.ⓘ Радиус кругового сектора [r] |
+10% -10% |
|
✖Периметр кругового сектора — это общая длина всех граничных ребер кругового сектора.ⓘ Периметр кругового сектора [P] |
⎘ копия |
Периметр кругового сектора Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Угол кругового сектора: 40 степень –> 0.698131700797601 Радиан (Проверьте преобразование здесь)
Радиус кругового сектора: 5 метр –> 5 метр Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
13.490658503988 метр –> Конверсия не требуется
3 Периметр кругового сектора Калькуляторы
Периметр кругового сектора формула
Периметр кругового сектора = (Угол кругового сектора+2)*Радиус кругового сектора
P = (∠Sector+2)*r
Что такое круговой сектор?
Круговой сектор — это, по сути, часть площади круга, прорезанная через два радиуса. Геометрически круговой сектор — это область, окруженная дугой окружности и соответствующими радиусами под определенным центральным углом.
Что такое Круг?
Окружность — это базовая двухмерная геометрическая фигура, которая определяется как совокупность всех точек на плоскости, находящихся на фиксированном расстоянии от фиксированной точки. Фиксированная точка называется центром круга, а фиксированное расстояние называется радиусом круга. Когда два радиуса становятся коллинеарными, эта общая длина называется диаметром круга. То есть диаметр — это длина отрезка внутри круга, проходящего через центр, и он будет в два раза больше радиуса.
В этом простом онлайн-калькуляторе для нахождения величин сектора круга можно быстро определить длину дуги сектора, зная площадь, периметр или центральный угол сектора. Для этого нужно заполнить по одному пустующему слота в калькуляторах окружности и сектора окружности, после чего нажать на кнопку “Рассчитать”. В результате высветятся все недостающие значения вместе с формулами.
Калькулятор окружности:
Достаточно заполнить только одну ячейку — остальное калькулятор посчитает сам.
Периметр или длина окружности (P)
Калькулятор сектора окружности:
Достаточно ввести только одно значение и указать радиус окружности — остальное калькулятор посчитает сам.
Центральный угол сектора в градусах (α)
Площадь сектора окружности (S1)
Калькулятор сегмента окружности:
Достаточно ввести только одно* значение и указать радиус окружности — остальное калькулятор посчитает сам.
Исключения:
* – при известном периметре (P2) нужно дополнительно указать длину дуги (l1) или хорды (c).
* – при известной площади (S2) нужно дополнительно указать длину хорды (c) или высоты (h).
Угол сегмента в градусах (α1)
Площадь сегмента окружности (S2)
Округление:
* – обязательно заполнить
Определения. Все приводимые определения эквивалентны:
- Сектор круга — это пересечение круга и некоторого его центрального угла.
- Сектор круга — это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром.
- Сектор круга — это часть угла, включающая точки удаленные от вершины угла не более чем на некоторое расстояние (радиус сектора).
Параметры сектора. Форму и размеры сектора полностью определяют два параметра:
- угол θ,
- радиус R.
Критерий конгруэнтности. Сектора, у которых совпадают оба параметры параметра R и θ, — конгруэнтны.
Критерий подобия. Сектора, у которых совпадают параметры θ, — подобны.
Площадь сектора:
- S = θR2/2, если угол θ выражен в радианах,
- S = (θ/360°)·πR2, если угол θ выражен в градусах.
Периметр сектора:
- P = (2 + θ)·R, если угол θ выражен в радианах,
- P = (2 + πθ/180°)·R, если угол θ выражен в градусах, а π — постоянная пи.
Частные случаи секторов:
- При θ = 0 получается вырожденный сектор, совпадающий с отрезком длиной R.
- У сектора с углом θ = 1 радиан (≈57°) длины всех сторон равны R, а периметр — 3R.
- Сектор с углом θ = 90° называется квадрантом; особенность квадранта: все три его угла имеют величину 90°.
- У сектора с углом θ = 2 радиана (≈114°) площадь равна квадрату радиуса R2.
- Сектор с углом θ = 180° представляет собой половину окружности; особенность: такой сектор имеет только 2 угла величиной 90°.
- При θ > 180° сектор становится невыпуклой фигурой.
- При θ = 360° сектор вырождается в полную окружность.
Дополнительные сектора. Любые два радиуса разбивают круг на пару секторов. Такие сектора называются взаимно дополнительными, их сумма углов составляет 360°.
Круговые диаграммы. Два или более радиусов разбивают круг на такое же число секторов, сумма углов которых составляет 360°. Это свойство используется при построении так называемых секторных (круговых) диаграмм, в которых вся окружность принимается за 100% некоторого ресурса, а отдельные сектора отражают его разделение по долям.
Развертка конуса. Любой невырожденный сектор представляет собой развертку конуса (без основания). Высоту h этого конуса можно найти по формуле:
- h = R√(1 — θ2/4π2), если угол θ выражен в радианах,
- h = R√(1 — (θ/360°)2), если угол θ выражен в градусах.
Источники:
- Википедия: Круг
- Википедия: Сектор (геометрия)
Дополнительно от Генона:
- Как найти площадь круга?
- Как найти длину хорды?
- Как найти площадь треугольника?
- Как вычислить площадь прямоугольного треугольника?
- Каково точное значение числа пи?

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).
На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота
Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:
Формулы вычисления параметров сегмента
Площадь сегмента:
[1]
Длина дуги:
Длина хорды:
Высота сегмента:
![]()
Сегмент
Угол в градусах, образуемый радиусами сектора
Точность вычисления
Знаков после запятой: 2
Однако, как справедливо заметил наш пользователь:«на практике часто случается, что как радиус дуги, так и угол неизвестны» (см. длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:
![]()
Параметры сегмента по хорде и высоте
Точность вычисления
Знаков после запятой: 2
Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:
Далее, зная радиус и длину хорды, легко найти угол сегмента по формуле:
Остальные параметры сегмента вычисляются аналогично первому калькулятору, по формулам, приведенным в начале статьи.
Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу:
![]()
Площадь сегмента круга по радиусу и высоте
Точность вычисления
Знаков после запятой: 2
Этот калькулятор вычисляет угол из высоты и радиуса по следующей формуле:
далее используется формула [1] для получения площади.
15 вычислений по сегменту круга в одной программе
Последний калькулятор включает в себя все оставшиеся вычисления параметров кругового сегмента:
- длина дуги
- угол
- хорда
- высота
- радиус
- площадь
Выберите два известных аргумента и калькулятор выдаст вам все оставшиеся.
![]()
Круговой сегмент – все варианты расчета
Точность вычисления
Знаков после запятой: 2
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
We will discuss the Area
and perimeter of a sector of a circle
We know that
Therefore,
Area of a sector of a circle = (frac{ theta^{circ}}{360^{circ}}) × Area of the circle = (frac{ θ}{360}) ∙ πr2
where r is the radius of the circle and (theta^{circ}) is the sectorial angle.
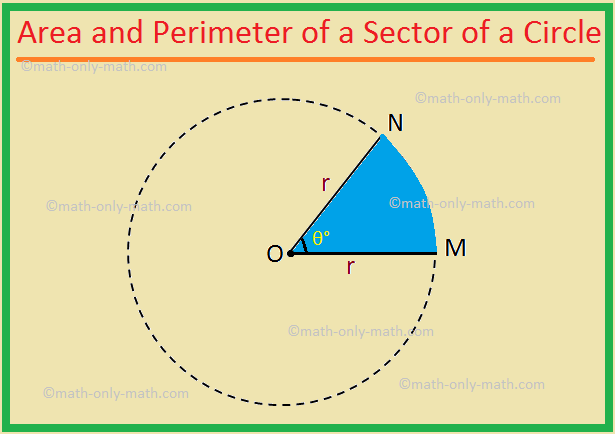
Also, we know that
![]()
Therefore,
Arc MN = (frac{ theta^{circ}}{360^{circ}}) ×
Circumference of the circle = (frac{ θ}{360}) ∙ 2πr = (frac{πθr}{180})
where r is the radius of the circle and (theta^{circ})
is the sectorial angle.
Thus,
perimeter of a sector of a circle = ((frac{πθ}{180}) ∙ r
+ 2r) = ((frac{πθ}{180}) + 2)r
where r is the radius of the circle and θ° is the sectorial
angle.
Problems on Area and Perimeter of a Sector of a Circle:
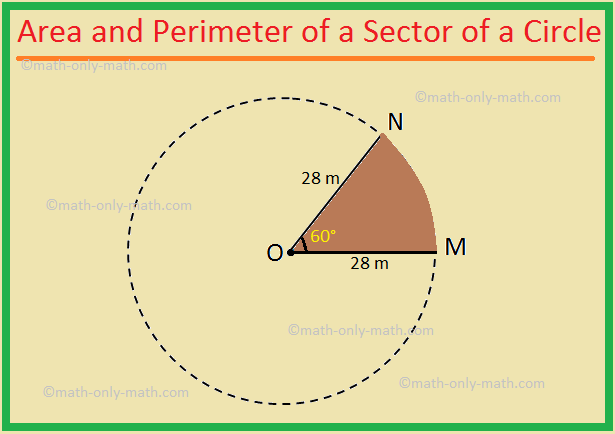
1. A plot of land is in the shape of a sector of a circle of
radius 28 m. If the sectorial angle (central angle) is 60°, find the area and
the perimeter of the plot. (Use π = (frac{22}{7}).)
Solution:
Area of the plot = (frac{60^{circ}}{360^{circ}}) × πr2 [Since θ = 60]
=
(frac{1}{6}) × πr2
=
(frac{1}{6}) × (frac{22}{7}) × 282 m2.
=
(frac{1}{6}) × (frac{22}{7}) × 784 m2.
=
(frac{17248}{42}) m2.
=
(frac{1232}{3}) m2.
=
410(frac{2}{3}) m2.
Perimeter of the plot = ((frac{πθ}{180}) + 2)r
= ((frac{22}{7}) ∙ (frac{60}{180}) + 2) 28 m
= ((frac{22}{21}) + 2) 28 m
= (frac{64}{21}) ∙ 28 m
= (frac{1792}{21}) m
= (frac{256}{3}) m
= 85(frac{1}{3}) m.
10th Grade Math
From Area and Perimeter of a Sector of a Circle to HOME PAGE
Didn’t find what you were looking for? Or want to know more information
about Math Only Math.
Use this Google Search to find what you need.
