Как найти периметр семиугольника 5 класс - Сайт, где вы сможете решить свои вопросы

Среди геометрических фигур очень большую часть составляют многоугольники. Это квадрат, прямоугольник, параллелограмм, ромб, треугольник, трапеция и другие n-угольники (n — количество сторон многоугольника).

Периметр любого многоугольника – это сумма длин всех его сторон.

Онлайн-калькулятор периметра многоугольника

Формула периметра многоугольника

Общая формула периметра многоугольника

P=a+b+c+d+e+…P=a+b+c+d+e+…,

где a,b,c,d,e,…a, b, c, d, e,… — длины сторон многоугольника.

Частным случаем многоугольника является так называемый правильный многоугольник.

Определение правильного многоугольника

Правильный многоугольник – это такой многоугольник, у которого все стороны равной длины.

Если говорить о периметре правильного многоугольника, то его можно найти, умножив длину стороны фигуры на количество сторон.

Периметр правильного многоугольника

P=n⋅aP=ncdot a

aa — длина стороны многоугольника;
nn — количество сторон многоугольника.

Разберем задачи на нахождение периметра правильного и неправильного многоугольников.

Задача 1

Найти периметр правильного шестиугольника со стороной 10 см.

Решение

a=10a=10
n=6n=6

Воспользуемся формулой для нахождения периметра правильного шестиугольника и подставим вместо aa численное значение:

P=n⋅a=6⋅10=60P=ncdot a=6cdot 10=60 см.

Ответ: P=60P=60 см.

Задача 2

Стороны многоугольника равны 6 см, 5 см, 2 см, 3 см и 1 см. Найти периметр данной фигуры.

Решение

a=6a=6
b=5b=5
c=2c=2
d=3d=3
e=1e=1

В данной задаче нам дан неправильный многоугольник, так как его стороны разной длины. В этом случае нам подходит первая стандартная формула нахождения периметра. Сложим длины всех сторон многоугольника и найдем его периметр:

P=a+b+c+d+e=6+5+2+3+1=17P=a+b+c+d+e=6+5+2+3+1=17 см.

Ответ: P=17P=17 см.

Ищете, где где можно заказать контрольную работу недорого? Обратитесь к нашим экспертам!

Тест по теме “Периметр многоугольника”

Источник

Периметр семиугольника Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. Преобразование входов в базовый блок

Сторона семиугольника: 10 метр –> 10 метр Конверсия не требуется

ШАГ 2: Оцените формулу

ШАГ 3: Преобразуйте результат в единицу вывода

70 метр –> Конверсия не требуется

8 Периметр семиугольника Калькуляторы

3 Периметр семиугольника Калькуляторы

Периметр семиугольника формула

Периметр семиугольника = 7*Сторона семиугольника

P = 7*S

что такое семиугольник?

Гептагон – это многоугольник с семью сторонами и семью вершинами. Как и любой многоугольник, семиугольник может быть выпуклым или вогнутым, как показано на следующем рисунке. Когда он выпуклый, все его внутренние углы меньше 180 °. С другой стороны, когда он вогнутый, один или несколько его внутренних углов больше 180 °. Когда все стороны семиугольника равны, он называется равносторонним.

Источник

Как найти периметр многоугольника

Здравствуйте!
Нужна помощь в вопросе «как найти периметр многоугольника». Помогите, пожалуйста!
Спасибо!

Разберемся, как найти периметр многоугольника.
Поскольку периметр фигуры — это сумма длин сторон этой фигуры, то и для многоугольника это будет длин всех сторон многоугольника или, другими словами, сумма всех расстояний между его углами (или вершинами).
С помощью формулы для общего случая n-угольника можно записать его периметр:

$[P_{n-ugoln}=st_1+st_2+st_3+dots +st_n.]$

Если все стороны n-угольника равны, то есть имеем дело с правильным n-угольником, то его периметр будет вычисляться по следующей формуле:

$[P_{n-ugoln}=ncdot storona.]$

Пример 1.
Стороны семиугольника равны 11 см, 13см, 17 см, 19 см, 23 см, 29 см, 31 см. Найдем его периметр.

Решение.
Периметр семиугольника будем находить по формуле:

$[P_{7-ugoln}=st_1+st_2+st_3+st_4+st_5+st_6+st_7.]$

$P_{7-ugoln}=11+13+17+19+23+29+31=143$

Подставим известные длины его сторон:
(см).

Ответ. $P_{7-ugoln}=143$ (см).

Пример 2.
Окружность с радиусом см вписана в правильный шестиугольник. Найдем периметр данного шестиугольника.

Решение.
Воспользуемся соотношением, которое связывает радиус вписанной в правильный шестиугольник окружности и его сторону:

$[radius=frac{storonacdot sqrt{3}}{2}.]$

Выразим из данного соотношения длину стороны:

$[11sqrt{13}=frac{storonacdot sqrt{3}}{2};]$

$storona=frac{2cdot 11sqrt{13}}{sqrt{3}}=22sqrt{frac{13}{3}}=22sqrt{4frac{1}{3}}$ (см).
Поскольку по условию задачи имеем правильный шестиугольник, то его периметр найдем с помощью следующей формулы:
$P_{6-ugoln}=6cdot storona=6cdot 22sqrt{4frac{1}{3}}=132sqrt{4frac{1}{3}}$ (см).

Ответ. $P_{6-ugoln}=132sqrt{4frac{1}{3}}$ (см).

Семиугольник, виды, свойства и формулы

Семиугольник – это многоугольник, общее количество углов (вершин) которого равно семи.

Семиугольник, выпуклый и невыпуклый семиугольник:

Семиугольник – это многоугольник с семью углами.

Семиугольник – это многоугольник, общее количество углов (вершин) которого равно семи.

Семиугольник может быть выпуклым и невыпуклым.

Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.

Соответственно выпуклый семиугольник – это семиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

Звёздчатый семиугольник – семиугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного семиугольника многоугольника. Стороны звёздчатого семиугольника могут пересекаться между собой.

Рис. 1. Выпуклый семиугольник

Рис. 2. Невыпуклый семиугольник

Сумма внутренних углов любого выпуклого семиугольника равна 900°.

Правильный семиугольник (понятие и определение):

Правильный семиугольник – это правильный многоугольник с семью сторонами.

В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.

Правильный семиугольник – это семиугольник, у которого все стороны равны, а все внутренние углы равны 128 4/7° ≈ 128,571°.

Рис. 3. Правильный семиугольник

Правильный семиугольник имеет 7 сторон, 7 углов и 7 вершин.

Углы правильного семиугольника образуют семь равнобедренных треугольников .

Правильный семиугольник можно невозможно построить с помощью циркуля и линейки, но можно построить с помощью циркуля и невсиса, то есть размеченной линейки, на которой можно делать отметки и с помощью которой можно проводить прямые, проходящие через какую-нибудь точку, причём отмеченные на линейке точки будут принадлежать данным линиям (прямым или окружностям).

Свойства правильного семиугольника:

1. Все стороны правильного семиугольника равны между собой.

2. Все углы равны между собой и составляют 128 4/7° ≈ 128,571°.

Рис. 4. Правильный семиугольник

3. Сумма внутренних углов любого правильного семиугольника равна 900°.

4. Все биссектрисы углов между сторонами равны и проходят через центр правильного семиугольника O.

Рис. 5. Правильный семиугольник

5. Количество диагоналей правильного семиугольника равно 14.

Рис. 6. Правильный семиугольник

6. Центр вписанной окружности O₁ совпадает с центром описанной окружности O₂, что и образуют центр многоугольника O.

Рис. 7. Правильный семиугольник

Формулы правильного семиугольника:

Пусть a – сторона семиугольника, r – радиус окружности, вписанной в семиугольник, R – радиус описанной окружности семиугольника, P – периметр семиугольника, S – площадь семиугольника.

Формулы стороны правильного семиугольника:

Формулы периметра правильного семиугольника:

Формулы площади правильного семиугольника:

Формулы радиуса окружности, вписанной в правильный семиугольник:

Семиугольник в природе, технике и культуре:

В некоторых странах, например, в Великобритании, некоторые монеты имеют правильную криволинейную семиугольную форму.

Формула расчета периметра многоугольника

Периметр многоугольника в геометрии — это результат сложения длин всех его сторон.

Свойства многоугольника

Все стороны прямые.
Стороны не пересекаются (кроме звездчатых).
Двумерная фигура.
Сумма внешних углов всегда равна 360º.
Сумма внутренних углов равна (frac2) (для правильных фигур).

Как вычислить периметр правильного многоугольника

Свойства правильного многоугольника

Все стороны равны.
Все углы равны.
Центр равно удален ото всех вершин и сторон.
Сумма всех углов равна 180º×(n−2).
Все внешние углы при сложении их градусных мер дадут 360º.
Все биссектрисы углов между сторонами равны и пересекают центр фигуры.
Возможно вписать окружность и описать круг. Площадь кольца зависит от длины стороны многоугольника.

Формула

где a — длина стороны, n — количество сторон.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Для неправильного многоугольника

Описание

У неправильного многоугольника все стороны разного размера.

Формула

Его периметр (P) можно рассчитать, сложив все длины его сторон (a, b, c,d и т.д.). Это первый способ.

Второй способ: если есть стороны с одинаковыми длинами, формулу можно сократить, использовав умножение.

Дан прямоугольник со сторонами 4см, 4см, 2см и 2см. Чтобы узнать периметр, можно просто их все сложить, как показано в формуле выше. А можно сделать так: 4×2+2×2, так как стороны попарно равны.

Этот способ подойдет и для фигур с большим количеством сторон, некоторые из которых равны.

Дан восьмиугольник со сторонами 5см, 5см, 3см, 3см, 3см, 2см и 1см. Периметр можно высчитать сложением, а можно считать так: 5×2+3×3+2+1.

По заданным координатам

Как начертить многоугольник

Еще один способ вычисления периметра многоугольника — построить фигуру на координатной прямой.

Для этого нужно:

Построить координатные оси.
Нанести на них заданные координаты (длины) сторон. Соединить точки.

Формула для расчета периметра

Далее нужно находить длины всех получившихся сторон.

Размеры прямых сторон легко узнавать методом подсчета координатных меток между точками сторон. Записать получившиеся значения рядом со сторонами.
Найти длину наклонных сторон. Это можно сделать по формуле: (d=sqrt)

В формулу нужно подставить вместо x и y координаты сторон.

3. Найти периметр сложением длин всех сторон по формуле для неправильного многоугольника: P=a+b+c+d. где a,b,c,d. — длины сторон. А если получился правильный: P=a×n, где a — длина стороны, а n — количество сторон фигуры.

Примеры решения задач

Задания приведены разного уровня сложности. Расположены по принципу «от простого к сложному».

Во всех задачах нужно найти периметр фигур. Этот вопрос дублироваться в каждом примере ниже не будет.

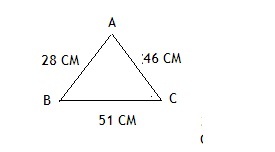
Пример 1

Дан треугольник ABC. AB=28см, BC=51см, AC=46см.

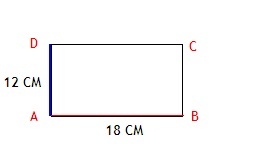
Пример 2

В прямоугольнике ABCD длина синей стороны 12 см, а красной 18 см.

Пример 3

Дан квадрат со стороной 12 см.

Мы знаем, что все стороны квадрата одинаковые. Их всего 4. Значит, P=12×4=48см.

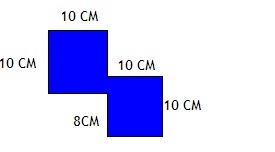
Пример 4

Дана фигура (данные на рисунке).

На рисунке мы видим восьмиугольник. У него шесть сторон по 10 см и две стороны по 8 см. Значит, P=10×6+8×2=60+16+76см.

Источник

Семиугольник, виды, свойства и формулы.

Семиугольник – это многоугольник, общее количество углов (вершин) которого равно семи.

Семиугольник, выпуклый и невыпуклый семиугольник

Правильный семиугольник (понятие и определение)

Свойства правильного семиугольника

Формулы правильного семиугольника

Семиугольник в природе, технике и культуре

Шестиугольник, семиугольник, восьмиугольник

Семиугольник, выпуклый и невыпуклый семиугольник:

Семиугольник – это многоугольник с семью углами.

Семиугольник – это многоугольник, общее количество углов (вершин) которого равно семи.

Семиугольник может быть выпуклым и невыпуклым.

Рис. 1. Выпуклый семиугольник

Рис. 2. Невыпуклый семиугольник

Сумма внутренних углов любого выпуклого семиугольника равна 900°.

Правильный семиугольник (понятие и определение):

Правильный семиугольник – это правильный многоугольник с семью сторонами.

В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.

Рис. 3. Правильный семиугольник

Правильный семиугольник имеет 7 сторон, 7 углов и 7 вершин.

Углы правильного семиугольника образуют семь равнобедренных треугольников.

Правильный семиугольник невозможно построить с помощью циркуля и линейки, но можно построить с помощью циркуля и невсиса, то есть размеченной линейки, на которой можно делать отметки и с помощью которой можно проводить прямые, проходящие через какую-нибудь точку, причём отмеченные на линейке точки будут принадлежать данным линиям (прямым или окружностям).

Свойства правильного семиугольника:

1. Все стороны правильного семиугольника равны между собой.

a₁ = a₂ = a₃ = a₄= a₅ = a₆ = a₇.

2. Все углы равны между собой и составляют 128 4/7° ≈ 128,571°.

α₁ = α₂ = α₃ = α₄ = α₅ = α₆ = α₇ = 128 4/7° ≈ 128,571°.

Рис. 4. Правильный семиугольник

3. Сумма внутренних углов любого правильного семиугольника равна 900°.

4. Все биссектрисы углов между сторонами равны и проходят через центр правильного семиугольника O.

Рис. 5. Правильный семиугольник

5. Количество диагоналей правильного семиугольника равно 14.

Рис. 6. Правильный семиугольник

Рис. 7. Правильный семиугольник

Формулы правильного семиугольника:

Формулы стороны правильного семиугольника:

Формулы периметра правильного семиугольника:

Формулы площади правильного семиугольника:

Формулы радиуса окружности, вписанной в правильный семиугольник:

Семиугольник в природе, технике и культуре:

Некоторые виды кактусовых имеют форму звездчатого семиугольника.

Прямоугольник

Прямоугольный треугольник

Равнобедренный треугольник

Равносторонний треугольник

Шестиугольник

Восьмиугольник

Коэффициент востребованности
2 371

Источник

yposoderouch

Вопрос по математике:

Найдите периметр семиугольника каждая сторона которого равна а)2 см б)5 см в)7 см

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!

Ответы и объяснения 1

rothedstesep379

Р=а×7
а)2×7=14см
Б)5×7=35см
В)7×7=49см

Знаете ответ? Поделитесь им!

Гость

Гость ?

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

Отвечать достоверно на те вопросы, на которые знаете
правильный ответ;
Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему;
Писать без грамматических, орфографических и
пунктуационных ошибок.

Этого делать не стоит:

Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения;
Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее;
Использовать мат – это неуважительно по отношению к
пользователям;
Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Математика.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!

Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.

Источник

Онлайн-калькулятор периметра многоугольника

Формула периметра многоугольника

Тест по теме “Периметр многоугольника”

Периметр семиугольника Решение

8 Периметр семиугольника Калькуляторы

3 Периметр семиугольника Калькуляторы

Периметр семиугольника формула

что такое семиугольник?

Как найти периметр многоугольника

Семиугольник, виды, свойства и формулы

Семиугольник, выпуклый и невыпуклый семиугольник:

Правильный семиугольник (понятие и определение):

Свойства правильного семиугольника:

Формулы правильного семиугольника:

Семиугольник в природе, технике и культуре:

Формула расчета периметра многоугольника

Свойства многоугольника

Как вычислить периметр правильного многоугольника

Свойства правильного многоугольника

Формула

Для неправильного многоугольника

Описание

Формула

По заданным координатам

Как начертить многоугольник

Формула для расчета периметра

Примеры решения задач

Семиугольник, виды, свойства и формулы.

Семиугольник, выпуклый и невыпуклый семиугольник:

Правильный семиугольник (понятие и определение):

Свойства правильного семиугольника:

Формулы правильного семиугольника:

Семиугольник в природе, технике и культуре:

Ответы и объяснения 1

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Есть сомнения?

Вам также может понравиться

Как найти название вай фай роутера

Как найти разведение раствора

Аватары клиента как составить

Добавить комментарий Отменить ответ