Правильный шестиугольник — это выпуклая многоугольная фигура с шестью сторонами одинаковой длины и
углами равной величины. Другое название — гексагон. Он имеет ряд следующих особенностей и
признаков:
- Длина стороны равнозначна радиусу описанной вокруг него окружности.
- Длинная диагональ представляет собой диаметр описанной окружности вокруг шестиугольника и её
числовое значение — это удвоенная величина стороны. - Короткая диагональ этой фигуры больше его стороны в √3 раза.
- Величина каждого из шести углов имеет значение 120 градусов.
- Короткая диагональ гексагона — это перпендикуляр к одной из его сторон.
- Прямоугольный треугольник, который образуется посредством одной из сторон данной фигуры, а также
его диагоналями — короткой и длинной, — имеет острые углы 30 и 60 градусов. - Если провести 6 длинных диагоналей, то образуется 6 правильных треугольников. Все их углы будут
по 60 градусов, а каждая высота равнозначна радиусу окружности, вписанной в данную фигуру.
Вариантов нахождения периметра гексагона существует множество. Например, с использованием диагоналей
и площади. Ведь по условию не всегда известна длина стороны.
- Периметр правильного шестиугольника через площадь
- Периметр правильного шестиугольника через короткую
диагональ - Периметр правильного шестиугольника через длинную
диагональ - Периметр правильного шестиугольника через радиус описанной
окружности - Периметр правильного шестиугольника через радиус вписанной
окружности - Периметр правильного шестиугольника через сторону
Через площадь
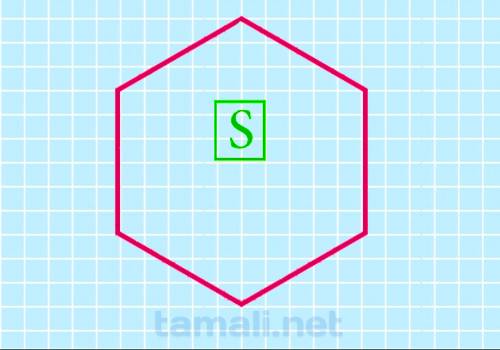
Если по условию известна только площадь, то и с этим исходным значением получится найти
периметр данной фигуры. Формула используется для этого следующая: a=sqrt(2/3*S/sqrt(3)).
Вычислив
значение «a», можно отыскать периметр, расчёт выглядит так:
P = 6*a
В данной и последующих формулах sqrt — это обозначение квадратного корня.
Площадь правильного
шестиугольника — это одна из основных числовых характеристик фигуры. С её помощью могут вычисляться
другие параметры, значение которых нужно найти в задании.
Находится по формуле: S=(3√3*a²)/2, где S
обозначается площадь правильного шестиугольника; «а» — длина его стороны.
Цифр после
запятой:
Результат в:
Через короткую диагональ
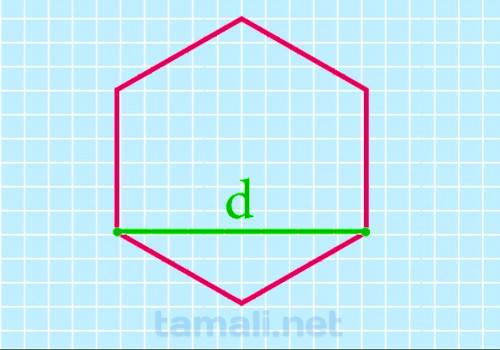
Меньшая диагональ гексагона — это величина отрезка, который соединяет одну его вершину с другой,
находящейся через один угол. Она в √3 раз больше его стороны. Отрезок отсекает в шестиугольнике
треугольник, который получается равнобедренным.
Для нахождения периметра в этом случае
используют следующую формулу:
P = 6 * (d/√3)
где d — короткая диагональ.
Цифр после
запятой:
Результат в:
Через длинную диагональ
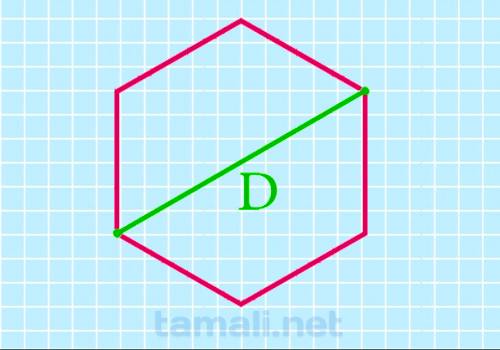
Длинная диагональ гексагона является отрезком, который проходит из одной вершины многоугольника до
противоположной. Противоположная вершина находится через два угла.
P = 3 * d
Большая диагональ шестиугольника правильной формы является диаметром описанной вокруг него окружности
и равна сумме двух его сторон. Соответственно, чтобы найти его периметр данным способом, нужно
умножить известную величину на 3.
Цифр после
запятой:
Результат в:
Через радиус описанной окружности
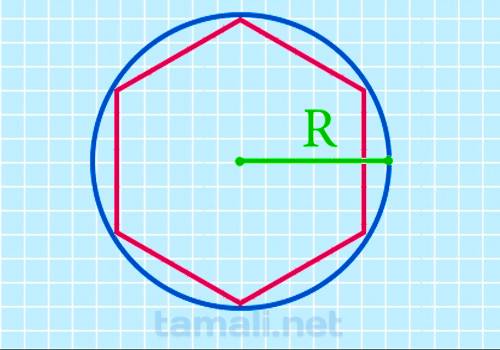
Радиус — отрезок, который идет из центра окружности к любой точке, расположенной на окружности.
Радиус описанной окружности вокруг гексагона равен длине одной его стороны.
Отсюда следует, что
P = 6 * r
где r — радиус описанной окружности.
Вокруг каждой правильной геометрической фигуры можно
описать окружность или вписать её внутрь. Правильный шестиугольник имеет только одну описанную
окружность. Периметр равен шести радиусам этой окружности.
Цифр после
запятой:
Результат в:
Через радиус вписанной окружности
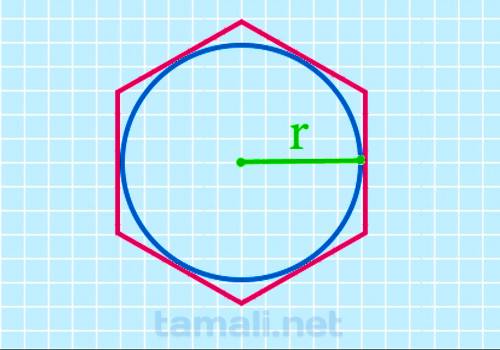
Также можно рассчитать периметр данной фигуры, если нам известен радиус вписанной в многоугольник
окружности . Искомая величина равна произведению четырёх корней из трёх и радиуса вписанной
окружности. Математическая формула выглядит так:
P = 4 * √3 * r
где r — радиус вписанной окружности.
Цифр после
запятой:
Результат в:
Через сторону
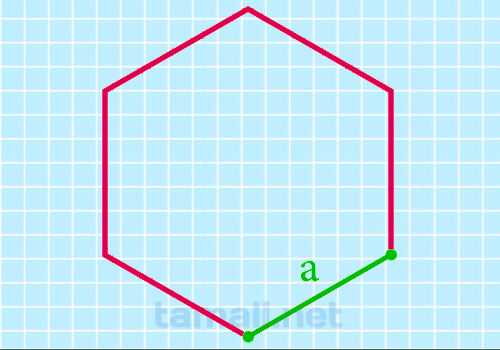
Периметр — это суммарная величина длин всех сторон плоской фигуры. Так как рассматривается
шестиугольник правильной формы, требуется измерить только одну из его сторон (здесь и далее она
обозначается как «а») и умножить на 6.
Р = 6 * a
Цифр после
запятой:
Результат в:
Данный способ очень простой, используется часто, но не является единственным. Так как значение
стороны может быть неизвестно, а по условию задачи будут доступны другие исходные данные.
Найти периметр любой фигуры легко, если знать необходимые формулы и правила, а также свойства и
признаки фигур. Иногда недостаточно применять только способ сложения длин всех сторон. Для этого
может не хватать исходных данных по условию, поэтому используют формулы с участием иных терминов.
Необходимо понимать и применять аксиомы, теоремы для решения подобных и других задач. Формулы,
разобранные выше, основаны на свойствах прямоугольных треугольников. (Теорема Пифагора, синусы
углов, косинусы углов и другие.)
Периметр шестиугольника с заданной площадью Калькулятор
| Search | ||
| Дом | математика ↺ | |
| математика | Геометрия ↺ | |
| Геометрия | 2D геометрия ↺ | |
| 2D геометрия | Шестиугольник ↺ | |
| Шестиугольник | Периметр шестиугольника ↺ |
|
✖Площадь шестиугольника — это общее количество плоскостей, заключенных между граничными линиями шестиугольника.ⓘ Площадь шестиугольника [A] |
+10% -10% |
|
✖Периметр шестиугольника — это общая длина всех граничных линий шестиугольника.ⓘ Периметр шестиугольника с заданной площадью [P] |
⎘ копия |
Периметр шестиугольника с заданной площадью Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Площадь шестиугольника: 95 Квадратный метр –> 95 Квадратный метр Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
36.2816567117923 метр –> Конверсия не требуется
9 Периметр шестиугольника Калькуляторы
3 Периметр шестиугольника Калькуляторы
Периметр шестиугольника с заданной площадью формула
Периметр шестиугольника = sqrt(8*sqrt(3)*Площадь шестиугольника)
P = sqrt(8*sqrt(3)*A)
Что такое шестиугольник?
Правильный шестиугольник определяется как равносторонний и равноугольный шестиугольник. Просто это шестисторонний правильный многоугольник. Он бицентрический, что означает, что он одновременно циклический (имеет описанную окружность) и тангенциальный (имеет вписанную окружность). Общая длина сторон равна радиусу описанной окружности или описанной окружности, которая равна 2/sqrt(3), умноженной на апофему (радиус вписанной окружности). Все внутренние углы равны 120 градусов. Правильный шестиугольник имеет шесть вращательных симметрий.
Правильный шестиугольник, многоугольнике с 6 вершинами, вычислить его параметры. Шестиугольник-это фигура, из которой можно складывать мозаику (черепицу). Введите одно из известных значений. Затем нажмите кнопку вычислить.
.
Поделиться расчетом:
Калькулятор шестиугольников
Длина стороны(a)
Большая диагональ(d1)
Меньшая диагональ(d2)
Периметр(p)
Площадь(S)
Радиус вписанной окружности(r)
Вычислить
Очистить
Формулы:

d2 = √3 * a
p = 6 * a
S = 3/2 * √3 * a2
r = √3 / 2 * a
Высота = d2 = 2 * r
Радиус окружности = a
Внутренние углы: 120°, 9 диагоналей





A polygon is a closed two-dimensional (2-D) shape composed of straight-line segments. In mathematics, a hexagon is a six-sided polygon. A regular hexagon is one in which the lengths of all the sides and the measurements of all the angles are equal. To look at it another way, the sides of a regular hexagon are congruent.
The area of a hexagon is the region that it occupies within its six sides. A hexagon is a closed polygon that consists of six-line segments and six internal angles. The name hexagon is derived from the Greek words ‘Hexa’ (six) and ‘Gonia’ (corners). The sum of internal angles in a hexagon is always 720°.
A hexagon is termed as a polygon with six sides. Hexagons are classified into three types: regular hexagons, irregular hexagons, and concave hexagons. A hexagon is called a regular hexagon if all of its sides are equal and all of its angles are the same.
Properties of Hexagon
- It is made up of six sides and six angles.
- All of the sides’ lengths and angles’ measurements are equal.
- A regular hexagon has a total of nine diagonals.
- The sum of all internal angles is 720 degrees, with each inside angle measuring 120 degrees.
- The sum of all external angles is 360 degrees, with each exterior angle measuring 60 degrees.
Hexagon Formula
Hexagon
A specified set of formulae for calculating the perimeter and area of a regular hexagon is known as the hexagon formula. The hexagon formula for a hexagon with side length s is as follows :
Area of Hexagon
The formula for Area of Hexagon is
Area = (3√3s2) / 2
here s is the side of hexagon
Perimeter of Hexagon
The formula of Perimeter of Hexagon is
Perimeter = 6s
here s is the side of Hexagon
Sample Problems
Problem 1: Calculate the perimeter and area of a regular hexagon having a side equal to 5 units.
Solution:
To Find : Perimeter and Area
Given : s = 5 units.
Using the hexagon formula for perimeter
Perimeter(P) = 6s
P = 6 × 5
P = 30 units
Using the regular hexagon formula for Area
= (3√3s2 ) / 2
= {(3√3(5)2 }/ 2
= {(3√3 (25)} / 2
= (3 x 1.7320 x 25 ) / 2
= 129.9/ 2
= 64.95 sq. unit
Therefore the perimeter of Hexagon is 30 units and area is 64.95 sq. units .
Problem 2: A hexagonal board which has a perimeter of 18 inches. Find its area.
Solution:
To Find : Area of the hexagon.
Given : Perimeter = 18 inches.
The perimeter of hexagon = 6s
18 = 6 s
s = 18/6
= 3 inches.
Using the hexagon formula for Area :
Area of hexagon
= { 3√3(3)2 } / 2
= { 3 x 1.7320 x 9 } / 2
= 46.764 / 2
= 23.382 sq. inches .
therefore the Area of hexagonal board is 23.382 sq . inches .
Problem 3: Determine the side of the regular hexagon whose perimeter is 30 units.
Solution:
To Find : Side of hexagon = s
Given : perimeter = 30 units.
Using the hexagon formula for perimeter
Perimeter(P) of hexagon = 6s
30 = 6 × s
s = 30/6 units
= 5 units
hence the side of hexagon is 5 units .
Problem 4: What is the area of a regular hexagon whose side length is equal to 6 cm?
Solution:
As we know ;
Area of hexagon = (3√3 s2)/2
Area = {3√3 (6)2 /2
Area = { 3 × 1.7320 × 36 } / 2
= 187.056/ 2
= 93.52 sq . cm
hence the area of hexagon is 93.52 sq . cm
Problem 5: Determine the side of the regular hexagon whose perimeter is 72 units.
Solution:
To Find : Side of hexagon = s
Given : perimeter = 72 units.
Using the hexagon formula for perimeter
Perimeter(P) of hexagon = 6s
72 = 6 × s
s = 72/6 units
= 12 units
hence the side of hexagon is 12 units .
Problem 6: What is the area of a regular hexagon whose side length is equal to 7 cm?
Solution:
As we know ;
Area of hexagon = (3√3 s2)/2
Area = {3√3 (7)2 } /2
Area = { 3 × 1.7320 × 49 } / 2
= 254.60 / 2
= 127.30 sq . cm
hence the area of hexagon is 127.30 sq . cm
Last Updated :
16 May, 2022
Like Article
Save Article
|
Периметр шестиугольника так же вычисляется как и периметр треугольника, четырехугольника… Периметр- это сумма длин всех сторон геометрической фигуры. Измеряйте длину каждой стороны вашего шестиугольника, запишите данные и сложите их. система выбрала этот ответ лучшим Невозмутимый Дождь 2 года назад Шестиугольник обладает периметром, который исчисляется по такой же формуле, по которой учащийся ищет периметры пятиугольников или треугольников. Но в формуле, касающейся шестиугольника, учитывается число его сторон, равное шести. При равенстве сторон длина одной стороны умножается на 6. Например: длина одной стороны – 3 сантиметра. 3 X 6 = 18. Получается, периметр шестиугольника равен 18-ти сантиметрам при условии, если его каждая сторона равна 3-ем сантиметрам. Если у шестиугольника разные стороны, то предыдущий способ вычисления периметра не подойдет. Здесь просто нужно сложить все стороны. К примеру, стороны шестиугольника равны 2,3,4,5,6,7 сантиметрам. Тогда делаем так: 2 + 3 + 4 + 5 + 6 + 7 = 27. То есть периметр нашего неправильного шестиугольника будет равен 27-ми сантиметрам. З В Ё Н К А 2 года назад Периметры шестиугольников представляют собой суммы всех отрезков, каждый из которых равен длине одной из их сторон. Таким образом, мы должны будем условно обозначить для удобства каждый угол такого шестиугольника. Например, буквами. Это сделано будет для того, чтобы измерять и суммировать отрезки, не путая их. Теперь по формуле типа “а + б + в + г… = P” мы ищем число, которое будет соответствовать периметру данной шестиугольной геометрической фигуры. Шесть углов – это шесть сторон. Следовательно, у нам должно быть ровно шесть слагаемых. На рисунке вы видите шестиугольник, правильным не являющийся: Например:
Прежде всего вспомним, что периметр любого многоугольника представлется собой сумму длин всех его сторон. Это самая простая и универсальная формула, которая подходит для вычисления периметра фигур, начиная от тругольника и заканчивая n-угольником. Квадраты, ромбы, равносторонние и равнобедренные треугольники, прямоугольники и так далее тоже относятся к многоугольникам. В каждом из вышеприведенных примеров, так же как и в правильных многоульниках, формулу для вычисления периметра можно “усовершенствовать”. В нашем случае, при условии, что шестиугольник является правильным, формула будет выглядеть следующим образом: P=6*a, где a – длина одной стороны. Если шестиугольник правильный, то для получения периметра надо умножить одну сторону на шесть. P = 6a. Также вокруг правильного шестиугольника можно нарисовать окружность. Радиус описанной окружности будет равен стороне. Потому, если по данным задачи известен радиус, то используем в формуле его. P = 6R. Если же по заданию окружность не описанная, а вписанная, то можно определить сторону правильно шестиугольника, исходя из радиуса. А уже после рассчитать периметр. a = 2r/√3. Если шестиугольник неправильный, то стороны будут отличаться и данные формулы применять нельзя. Тогда исходим уже из исходящих данных. ИнгаМус 8 лет назад Чтобы найти периметр шестиугольника, помню еще с уроков математики, надо знать длину каждой его стороны. Или просто измерить каждую его сторону. А затем надо сложить все полученные измерения и мы получим периметр. Анна Сергеевна 1984 8 лет назад Чтобы найти периметр многоугольника, нужно сложить длины его сторон. Валерий Альбертович 2 года назад Шестиугольники бывают разные, как и способы найти их периметры. Если речь идёт про правильный шестиугольник, то периметр будет вычисляться как длина стороны, умноженная на количество сторон, то есть в случае шестиугольника: P = 6*a, где а – сторона шестиугольника Если же шестиугольник, к примеру, неправильный, то достаточно просто сложить все его стороны, тогда получится периметр (это относится ко всем периметрам). bezdelnik 8 лет назад Шестиугольники могут быть разными: выпуклыми, с прямолинейными сторонами или с криволинейными, правильными у которого все стороны равны или неправильными. Периметр любого многоугольника равен сумме длин всех его сторон. Определенный ответ можно дать только о периметре правильного выпуклого прямолинейного шестиугольника вписанного в окружность с радиусом равным 1. Периметр такого шестиугольника равен 6-ти радиусам. валентин1943 8 лет назад Периметр правильного шестиугольника равен трём его центральным хордам, соединяющим противоположные вершины(или трём диаметрам описывающей шестигранник окружности).Если этот шестигранник неправильный и находится на пересеченной местности, то можно пройтись по его сторонам с шагомером. anna95 2 года назад Периметр шестиугольника можно найти так же как и у любой другой геометрической фигуры. Нужно измерить все его стороны и просто сложить, получившаяся сумма и будет периметром шестиугольника. Здесь ничего сложного нет. Знаете ответ? |



