From Wikipedia, the free encyclopedia
The first seven iterations in animation
Zooming into a vertex of the Koch curve
Zooming into a point that is not a vertex may cause the curve to rotate
First four iterations
Sixth iteration
The Koch snowflake (also known as the Koch curve, Koch star, or Koch island[1][2]) is a fractal curve and one of the earliest fractals to have been described. It is based on the Koch curve, which appeared in a 1904 paper titled “On a Continuous Curve Without Tangents, Constructible from Elementary Geometry”[3] by the Swedish mathematician Helge von Koch.
The Koch snowflake can be built up iteratively, in a sequence of stages. The first stage is an equilateral triangle, and each successive stage is formed by adding outward bends to each side of the previous stage, making smaller equilateral triangles. The areas enclosed by the successive stages in the construction of the snowflake converge to 
Construction[edit]
The Koch snowflake can be constructed by starting with an equilateral triangle, then recursively altering each line segment as follows:
- divide the line segment into three segments of equal length.
- draw an equilateral triangle that has the middle segment from step 1 as its base and points outward.
- remove the line segment that is the base of the triangle from step 2.
The first iteration of this process produces the outline of a hexagram.
The Koch snowflake is the limit approached as the above steps are followed indefinitely. The Koch curve originally described by Helge von Koch is constructed using only one of the three sides of the original triangle. In other words, three Koch curves make a Koch snowflake.
A Koch curve–based representation of a nominally flat surface can similarly be created by repeatedly segmenting each line in a sawtooth pattern of segments with a given angle.[4]
A fractal rough surface built from multiple Koch curve iterations
Properties[edit]
Perimeter of the Koch snowflake[edit]
Each iteration multiplies the number of sides in the Koch snowflake by four, so the number of sides after 
If the original equilateral triangle has sides of length 

an inverse power of three multiple of the original length.
The perimeter of the snowflake after 
The Koch curve has an infinite length, because the total length of the curve increases by a factor of 




Limit of perimeter[edit]
As the number of iterations tends to infinity, the limit of the perimeter is:
since 
An 
Area of the Koch snowflake[edit]
In each iteration a new triangle is added on each side of the previous iteration, so the number of new triangles added in iteration 
The area of each new triangle added in an iteration is 

where 

The total area of the snowflake after 
Collapsing the geometric sum gives:
Limits of area[edit]
The limit of the area is:
since 
Thus, the area of the Koch snowflake is 

Solid of revolution[edit]
The volume of the solid of revolution of the Koch snowflake about an axis of symmetry of the initiating equilateral triangle of unit side is 
Other properties[edit]
The Koch snowflake is self-replicating with six smaller copies surrounding one larger copy at the center. Hence, it is an irrep-7 irrep-tile (see Rep-tile for discussion).
The fractal dimension of the Koch curve is 


The Koch curve is continuous everywhere, but differentiable nowhere.
Tessellation of the plane[edit]
It is possible to tessellate the plane by copies of Koch snowflakes in two different sizes. However, such a tessellation is not possible using only snowflakes of one size. Since each Koch snowflake in the tessellation can be subdivided into seven smaller snowflakes of two different sizes, it is also possible to find tessellations that use more than two sizes at once.[8] Koch snowflakes and Koch antisnowflakes of the same size may be used to tile the plane.
Thue–Morse sequence and turtle graphics[edit]
A turtle graphic is the curve that is generated if an automaton is programmed with a sequence.
If the Thue–Morse sequence members are used in order to select program states:
the resulting curve converges to the Koch snowflake.
Representation as Lindenmayer system[edit]
The Koch curve can be expressed by the following rewrite system (Lindenmayer system):
- Alphabet : F
- Constants : +, −
- Axiom : F
- Production rules:
- F → F+F–F+F
Here, F means “draw forward”, – means “turn right 60°”, and + means “turn left 60°”.
To create the Koch snowflake, one would use F–F–F (an equilateral triangle) as the axiom.
Variants of the Koch curve[edit]
Following von Koch’s concept, several variants of the Koch curve were designed, considering right angles (quadratic), other angles (Cesàro), circles and polyhedra and their extensions to higher dimensions (Sphereflake and Kochcube, respectively)
| Variant (dimension, angle) | Illustration | Construction |
|---|---|---|
| ≤1D, 60-90° angle |  Cesàro fractal (85°) |
The Cesàro fractal is a variant of the Koch curve with an angle between 60° and 90°.[citation needed]  First four iterations of a Cesàro antisnowflake (four 60° curves arranged in a 90° square) |
| ≈1.46D, 90° angle |  Quadratic type 1 curve |
 First two iterations |
| 1.5D, 90° angle |  Quadratic type 2 curve |
Minkowski Sausage[9]  First two iterations. Its fractal dimension equals  and is exactly half-way between dimension 1 and 2. It is therefore often chosen when studying the physical properties of non-integer fractal objects. and is exactly half-way between dimension 1 and 2. It is therefore often chosen when studying the physical properties of non-integer fractal objects.
|
| ≤2D, 90° angle |  Third iteration |
Minkowski Island 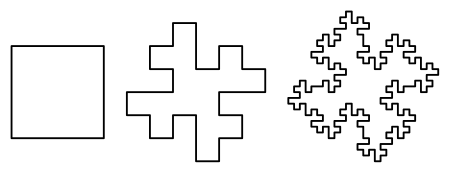 Four quadratic type 2 curves arranged in a square |
| ≈1.37D, 90° angle |  Quadratic flake |
 4 quadratic type 1 curves arranged in a polygon: First two iterations. Known as the “Minkowski Sausage”,[10][11][12] its fractal dimension equals  .[13] .[13]
|
| ≤2D, 90° angle | Quadratic antiflake |
Anticross-stitch curve, the quadratic flake type 1, with the curves facing inwards instead of outwards (Vicsek fractal) |
| ≈1.49D, 90° angle |  Quadratic Cross |
Another variation. Its fractal dimension equals  . .
|
| ≤2D, 90° angle |  Quadratic island[14] |
 Quadratic curve, iterations 0, 1, and 2; dimension of 
|
| ≤2D, 60° angle |  von Koch surface |
 First three iterations of a natural extension of the Koch curve in two dimensions. |
| ≤2D, 90° angle |  First (blue block), second (plus green blocks), third (plus yellow blocks) and fourth (plus transparent blocks) iterations of the type 1 3D Koch quadratic fractal |
Extension of the quadratic type 1 curve. The illustration at left shows the fractal after the second iteration  Animation quadratic surface |
| ≤3D, any |  Koch curve in 3D |
A three-dimensional fractal constructed from Koch curves. The shape can be considered a three-dimensional extension of the curve in the same sense that the Sierpiński pyramid and Menger sponge can be considered extensions of the Sierpinski triangle and Sierpinski carpet. The version of the curve used for this shape uses 85° angles. |
Squares can be used to generate similar fractal curves. Starting with a unit square and adding to each side at each iteration a square with dimension one third of the squares in the previous iteration, it can be shown that both the length of the perimeter and the total area are determined by geometric progressions. The progression for the area converges to 

The total area covered at the 
while the total length of the perimeter is:
which approaches infinity as 
See also[edit]
- List of fractals by Hausdorff dimension
- Gabriel’s Horn (infinite surface area but encloses a finite volume)
- Gosper curve (also known as the Peano–Gosper curve or flowsnake)
- Osgood curve
- Self-similarity
- Teragon
- Weierstrass function
- Coastline paradox
References[edit]
- ^ Addison, Paul S. (1997). Fractals and Chaos: An Illustrated Course. Institute of Physics. p. 19. ISBN 0-7503-0400-6.
- ^ Lauwerier, Hans (1991). Fractals: Endlessly Repeated Geometrical Figures. Translated by Gill-Hoffstädt, Sophia. Princeton University Press. p. 36. ISBN 0-691-02445-6.
Mandelbrot called this a Koch island.
- ^ von Koch, Helge (1904). “Sur une courbe continue sans tangente, obtenue par une construction géométrique élémentaire”. Arkiv för matematik, astronomi och fysik (in French). 1: 681–704. JFM 35.0387.02.
- ^ Alonso-Marroquin, F.; Huang, P.; Hanaor, D.; Flores-Johnson, E.; Proust, G.; Gan, Y.; Shen, L. (2015). “Static friction between rigid fractal surfaces” (PDF). Physical Review E. 92 (3): 032405. Bibcode:2015PhRvE..92c2405A. doi:10.1103/PhysRevE.92.032405. hdl:2123/13835. PMID 26465480. — Study of fractal surfaces using Koch curves.
- ^ Zhu, Zhi Wei; Zhou, Zuo Ling; Jia, Bao Guo (October 2003). “On the Lower Bound of the Hausdorff Measure of the Koch Curve”. Acta Mathematica Sinica. 19 (4): 715–728. doi:10.1007/s10114-003-0310-2. S2CID 122517792.
- ^ “Koch Snowflake”. ecademy.agnesscott.edu.
- ^ McCartney, Mark (2020-04-16). “The area, centroid and volume of revolution of the Koch curve”. International Journal of Mathematical Education in Science and Technology. 52 (5): 782–786. doi:10.1080/0020739X.2020.1747649. ISSN 0020-739X. S2CID 218810213.
- ^ Burns, Aidan (1994). “Fractal tilings”. Mathematical Gazette. 78 (482): 193–6. doi:10.2307/3618577. JSTOR 3618577. S2CID 126185324..
- ^ Paul S. Addison, Fractals and Chaos: An illustrated course, p. 19, CRC Press, 1997 ISBN 0849384435.
- ^ Weisstein, Eric W. (1999). “Minkowski Sausage”, archive.lib.msu.edu. Accessed: 21 September 2019.
- ^ Pamfilos, Paris. “Minkowski Sausage”, user.math.uoc.gr/~pamfilos/. Accessed: 21 September 2019.
- ^ Weisstein, Eric W. “Minkowski Sausage”. MathWorld. Retrieved 22 September 2019.
- ^ Mandelbrot, B. B. (1983). The Fractal Geometry of Nature, p.48. New York: W. H. Freeman. ISBN 9780716711865. Cited in Weisstein, Eric W. “Minkowski Sausage”. MathWorld. Retrieved 22 September 2019..
- ^ Appignanesi, Richard; ed. (2006). Introducing Fractal Geometry. Icon. ISBN 978-1840467-13-0.
- ^ Demonstrated by James McDonald in a public lecture at KAUST University on January 27, 2013. “KAUST | Academics | Winter Enrichment Program”. Archived from the original on 2013-01-12. Retrieved 2013-01-29. retrieved 29 January 2013.
Further reading[edit]
- Kasner, Edward; Newman, James (2001) [1940]. “IX Change and Changeability § The snowflake”. Mathematics and the Imagination. Dover Press. pp. 344–351. ISBN 0-486-41703-4.
External links[edit]
Wikimedia Commons has media related to Koch curve.
| External video |
|---|
|
- (2000) “von Koch Curve”, efg’s Computer Lab at the Wayback Machine (archived 20 July 2017)
- The Koch Curve poem by Bernt Wahl, Wahl.org. Retrieved 23 September 2019.
- Weisstein, Eric W. “Koch Snowflake”. MathWorld. Retrieved 23 September 2019.
- “7 iterations of the Koch curve”. Wolfram Alpha Site. Retrieved 23 September 2019.
- “Square Koch Fractal Curves”. Wolfram Demonstrations Project. Retrieved 23 September 2019.
- “Square Koch Fractal Surface”. Wolfram Demonstrations Project. Retrieved 23 September 2019.
- Application of the Koch curve to an antenna
- A WebGL animation showing the construction of the Koch surface, tchaumeny.github.io. Retrieved 23 September 2019.
- “A mathematical analysis of the Koch curve and quadratic Koch curve” (PDF). Archived from the original (pdf) on 26 April 2012. Retrieved 22 November 2011.
Фрактальная и математическая кривая 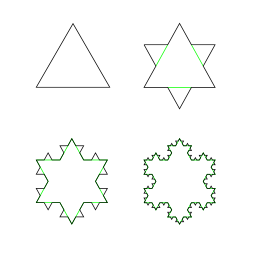




Снежинка Коха (также известная как кривая Коха, звезда Коха или остров Коха ) – это фрактальная кривая и один из самых ранних фракталов, которые были описаны. Он основан на кривой Коха, появившейся в 1904 году в статье шведского математика «На непрерывной кривой без касательных, построенной из элементарной геометрии» Хельге фон Кох.
Снежинка Коха может быть построена итеративно, в последовательности этапов. Первый этап представляет собой равносторонний треугольник, и каждый последующий этап формируется путем добавления внешних изгибов к каждой стороне предыдущего этапа, образуя меньшие равносторонние треугольники. Площади, окруженные последовательными стадиями построения снежинки, сходятся в 8/5 раз больше площади исходного треугольника, в то время как периметры последовательных стадий неограниченно увеличиваются. Следовательно, снежинка охватывает ограниченную площадь, но имеет бесконечный периметр.
Содержание
- 1 Конструкция
- 2 Свойства
- 2.1 Периметр снежинки Коха
- 2.1.1 Предел периметра
- 2.2 Площадь снежинки Коха
- 2.2.1 Границы площади
- 2.2.2 Твердое тело вращения
- 2.3 Другие свойства
- 2.1 Периметр снежинки Коха
- 3 Тесселяция плоскости
- 4 Последовательность Туэ – Морса и черепаха графика
- 5 Представление в виде системы Линденмайера
- 6 Варианты кривой Коха
- 7 См. также
- 8 Ссылки
- 9 Дополнительная литература
- 10 Внешние ссылки
Строительство
Снежинку Коха можно построить, начав с равностороннего треугольника, а затем рекурсивно изменив каждый сегмент линии следующим образом:
- разделив сегмент линии на три сегмента равной длины.
- draw равносторонний треугольник, у которого средний сегмент из шага 1 является его основанием и направлен наружу.
- удалить линейный сегмент, являющийся основанием треугольника из шага 2.
Первая итера ция этого процесса создает контур гексаграммы.
Снежинка Коха – это предел, к которому приближается, поскольку вышеуказанные шаги выполняются бесконечно. Кривая Коха, первоначально описанная Хельге фон Кохом, построена с использованием только одной из трех сторон исходного треугольника. Другими словами, три кривые Коха образуют снежинку Коха.
Представление номинально плоской поверхности на основе кривой Коха можно аналогичным образом создать, многократно сегментируя каждую линию в виде пилообразного узора сегментов с заданным углом.
Фрактальная шероховатая поверхность, построенная из нескольких итераций кривой Коха
Свойства
Периметр снежинки Коха
Каждая итерация умножает количество сторон снежинки Коха на четыре, поэтому количество сторон после n итераций определяется как:
- N N знак равно N N – 1 ⋅ 4 знак равно 3 ⋅ 4 N. { displaystyle N_ {n} = N_ {n-1} cdot 4 = 3 cdot 4 ^ {n} ,.}
Если исходный равносторонний треугольник имеет стороны длиной s, длина каждой стороны снежинка после n итераций:
- S n = S n – 1 3 = s 3 n, { displaystyle S_ {n} = { frac {S_ {n-1}} {3}} = { frac {s} {3 ^ {n}}} ,,}
обратная степень, равная трем кратным исходной длине. Периметр снежинки после n итераций равен:
- P n = N n ⋅ S n = 3 ⋅ s ⋅ (4 3) n. { displaystyle P_ {n} = N_ {n} cdot S_ {n} = 3 cdot s cdot { left ({ frac {4} {3}} right)} ^ {n} ,. }
Кривая Коха имеет бесконечную длину, потому что общая длина кривой увеличивается в 4/3 раза с каждой итерацией. Каждая итерация создает в четыре раза больше линейных сегментов, чем в предыдущей итерации, причем длина каждого из них составляет 1/3 длины сегментов на предыдущем этапе. Следовательно, длина кривой после n итераций будет (4/3) раз больше периметра исходного треугольника и не ограничена, поскольку n стремится к бесконечности.
Предел периметра
Поскольку количество итераций стремится к бесконечности, предел периметра равен:
- lim n → ∞ P n = lim n → ∞ 3 ⋅ s ⋅ ( 4 3) N = ∞, { Displaystyle lim _ {n rightarrow infty} P_ {n} = lim _ {n rightarrow infty} 3 cdot s cdot left ({ frac {4} {3}} right) ^ {n} = infty ,,}
начиная с | 4/3 |>1.
Трехмерная мера ln 4 / ln существует, но до сих пор не рассчитана. Были изобретены только верхняя и нижняя границы.
Площадь снежинки Коха
На каждой итерации новый треугольник добавляется с каждой стороны предыдущей итерации, поэтому количество новых треугольников добавляется в итерация n:
- T n = N n – 1 = 3 ⋅ 4 n – 1 = 3 4 ⋅ 4 n. { displaystyle T_ {n} = N_ {n-1} = 3 cdot 4 ^ {n-1} = { frac {3} {4}} cdot 4 ^ {n} ,.}
Площадь каждого нового треугольника, добавленного на итерации, составляет 1/9 площади каждого треугольника, добавленного на предыдущей итерации, поэтому площадь каждого треугольника, добавленного на итерации n, составляет:
- an = an – 1 9 = a 0 9 п. { displaystyle a_ {n} = { frac {a_ {n-1}} {9}} = { frac {a_ {0}} {9 ^ {n}}} ,.}
где a 0 – площадь исходного треугольника. Таким образом, общая новая площадь, добавленная на итерации n, составляет:
- bn = T n ⋅ an = 3 4 ⋅ (4 9) n ⋅ a 0 { displaystyle b_ {n} = T_ {n} cdot a_ {n} = { frac {3} {4}} cdot { left ({ frac {4} {9}} right)} ^ {n} cdot a_ {0}}
Общая площадь снежинка после n итераций:
- A n = a 0 + ∑ k = 1 nbk = a 0 (1 + 3 4 ∑ k = 1 n (4 9) k) = a 0 (1 + 1 3 ∑ k = 0 п – 1 (4 9) л). { displaystyle A_ {n} = a_ {0} + sum _ {k = 1} ^ {n} b_ {k} = a_ {0} left (1 + { frac {3} {4}} сумма _ {k = 1} ^ {n} left ({ frac {4} {9}} right) ^ {k} right) = a_ {0} left (1 + { frac {1} {3}} sum _ {k = 0} ^ {n-1} left ({ frac {4} {9}} right) ^ {k} right) ,.}
Сворачивание геометрическая сумма дает:
- A n = a 0 (1 + 3 5 (1 – (4 9) n)) = a 0 5 (8 – 3 (4 9) n). { displaystyle A_ {n} = a_ {0} left (1 + { frac {3} {5}} left (1- left ({ frac {4} {9}} right) ^ { n} right) right) = { frac {a_ {0}} {5}} left (8-3 left ({ frac {4} {9}} right) ^ {n} right) ,.}
Границы области
Границы области:
- lim n → ∞ A n = lim n → ∞ a 0 5 ⋅ (8 – 3 (4 9) п) знак равно 8 5 ⋅ a 0, { displaystyle lim _ {n rightarrow infty} A_ {n} = lim _ {n rightarrow infty} { frac {a_ {0}} {5}} cdot left (8-3 left ({ frac {4} {9}} right) ^ {n} right) = { frac {8} {5}} cdot a_ {0} ,,}
с | 4/9 |< 1.
Таким образом, площадь снежинки Коха составляет 8/5 площади исходного треугольника. Выраженный в терминах длины стороны s исходного треугольника, это:
- 2 s 2 3 5. { displaystyle { frac {2s ^ {2} { sqrt {3}}} {5}}.}
Твердое тело вращения
Объем тела вращения снежинки Коха относительно оси симметрии исходного равностороннего треугольника единичной стороны составляет 11 3 135 π. { displaystyle { frac {11 { sqrt {3}}} {135}} pi.}
Другие свойства
Снежинка Коха самовоспроизводится с шестью меньшими копиями, окружающими одну большую копию в центре. Следовательно, это реплика-7 реплика (см. Реп-плитка для обсуждения).
фрактальная размерность кривой Коха ln 4 / ln 3 ≈ 1,26186. Это больше, чем у линии (= 1), но меньше, чем у кривой Пеано, заполняющей пространство (= 2).
Кривая Коха непрерывна везде, но дифференцируема нигде.
Тесселяция плоскости

Можно мозаику плоскости копиями снежинок Коха двух разных размеров. Однако такая мозаика невозможна с использованием снежинок только одного размера. Так как каждую снежинку Коха в тесселяции можно разделить на семь меньших снежинок двух разных размеров, также можно найти тесселяцию, в которой одновременно используется более двух размеров. Для облицовки плоскости можно использовать снежинки Коха и антиснежинки Коха одинакового размера.
Последовательность Туэ – Морзе и графика черепахи
A графика черепахи – это кривая, которая генерируется, если автомат запрограммирован с помощью последовательности. Если элементы последовательности Туэ – Морзе используются для выбора состояний программы:
- Если t (n) = 0, двигаться вперед на одну единицу,
- Если t (n) = 1, повернуть против часовой стрелки на угол π / 3,
полученная кривая сходится к снежинке Коха.
Представление в виде системы Линденмайера
Кривая Коха может быть выражена следующей системой перезаписи (системой Линденмайера ):
- Алфавит : F
- Константы : +, –
- Аксиома : F
- Правила производства :
- F → F + F – F + F
Здесь F означает «рисовать вперед », – означает« повернуть направо на 60 ° », а + означает« повернуть налево на 60 ° ».
Чтобы создать снежинку Коха, можно использовать F – F – F (равносторонний треугольник) в качестве аксиомы.
Варианты кривой Коха
Следуя концепции фон Коха, было разработано несколько вариантов кривой Коха с учетом прямых углов (квадратичный ), других углов (Чезаро ), окружности и многогранники и их расширения в более высокие измерения (Sphereflake и Kochcube, соответственно)
| Вариант (измерение, угол ) | Иллюстрация | Конструкция |
|---|---|---|
| ≤1D, угол 60-90 ° |  фрактал Чезаро (85 °) фрактал Чезаро (85 °) |
Фрактал Чезаро – вариант кривой Коха с углом от 60 ° до 90 °.  Первая четыре итерации антиснежинки Cesàro (четыре кривые 60 °, расположенные в квадрате 90 °) Первая четыре итерации антиснежинки Cesàro (четыре кривые 60 °, расположенные в квадрате 90 °) |
| ≈1,46D, угол 90 ° |  Квадратичная кривая 1 типа Квадратичная кривая 1 типа |
 Первые две итерации Первые две итерации |
| 1,5D, угол 90 ° |  Квадратичная кривая типа 2 Квадратичная кривая типа 2 |
Колбаса Минковского  Первые две итерации. Ее фрактальная размерность равна 3/2 и находится точно посередине между размерностью 1 и 2. Поэтому ее часто выбирают при изучении физических свойств не -целые фрактальные объекты. Первые две итерации. Ее фрактальная размерность равна 3/2 и находится точно посередине между размерностью 1 и 2. Поэтому ее часто выбирают при изучении физических свойств не -целые фрактальные объекты. |
| ≤2D, угол 90 ° |  Третья итерация Третья итерация |
Остров Минковского  Четыре квадратичные кривые типа 2, расположенные в виде квадрата Четыре квадратичные кривые типа 2, расположенные в виде квадрата |
| ≈1,37D, угол 90 ° |  Квадратичная пластинка Квадратичная пластинка |
 4 квадратичных кривых типа 1, расположенных в виде многоугольника: Первая две итерации. Известная как «колбаса Минковского », ее фрактальная размерность равна ln 3 / ln √5 = 1,36521. 4 квадратичных кривых типа 1, расположенных в виде многоугольника: Первая две итерации. Известная как «колбаса Минковского », ее фрактальная размерность равна ln 3 / ln √5 = 1,36521. |
| ≤2D, угол 90 ° | Anti cross- стежковая кривая, квадратный чешуйчатый тип 1, с кривыми, обращенными внутрь, а не наружу (фрактал Вичека ) | |
| ≈1.49D, угол 90 ° |  Квадратичный крест Квадратичный крест |
Другой вариант. Его фрактальная размерность равно ln 3,33 / ln √5 = 1,49. |
| ≤2D, угол 90 ° |  Квадратичный остров Квадратичный остров |
 Квадратичная кривая, итерации 0, 1 и 2; размерность ln 18 / ln 6≈1,61 Квадратичная кривая, итерации 0, 1 и 2; размерность ln 18 / ln 6≈1,61 |
| ≤2D, угол 60 ° |  поверхность фон Коха поверхность фон Коха |
 Первые три итерации естественного продолжения кривой Коха в двух измерениях. Первые три итерации естественного продолжения кривой Коха в двух измерениях. |
| ≤2D, угол 90 ° |  Квадратичная поверхность типа 1 Квадратичная поверхность типа 1 |
Расширение квадратичной кривой типа 1. На иллюстрации слева показан фрактал после второй итерации  Анимационная квадратичная поверхность. Анимационная квадратичная поверхность. |
| ≤3D, любая |  кривая Коха в 3D кривая Коха в 3D |
Трехмерный фрактал, построенный из кривых Коха Эту форму можно рассматривать как трехмерное продолжение кривой в в том же смысле, что пирамида Серпинского и губка Менгера могут считаться продолжением треугольника Серпинского и ковра Серпинского. Версия кривой, используемая для этой формы, использует углы 85 °. |
Квадраты могут использоваться для создания подобных фрактальных кривых. Начиная с единичного квадрата и добавляя к каждой стороне на каждой итерации квадрат с размером, равным одной трети квадратов на предыдущей итерации, можно показать, что и длина периметра, и общая площадь определяются геометрической прогрессией. Прогрессия для площади сходится к 2, в то время как прогрессия для периметра расходится до бесконечности, так что, как и в случае снежинки Коха, у нас есть конечная площадь, ограниченная бесконечной фрактальной кривой. Результирующая область заполняет квадрат с тем же центром, что и исходная, но в два раза больше площади, и поворачивается на π / 4 радиан, причем периметр соприкасается, но никогда не перекрывается.
Общая площадь, покрываемая на n-й итерации, составляет:
- A n = 1 5 + 4 5 ∑ k = 0 n (5 9) k, что дает lim n → ∞ A n = 2, { displaystyle A_ {n} = { frac {1} {5}} + { frac {4} {5}} sum _ {k = 0} ^ {n} left ({ frac {5} {9} } right) ^ {k} quad { mbox {give}} quad lim _ {n rightarrow infty} A_ {n} = 2 ,,}
, а общая длина периметра равна :
- п n = 4 (5 3) na, { displaystyle P_ {n} = 4 left ({ frac {5} {3}} right) ^ {n} a ,,}
который приближается к бесконечности при увеличении n.
См. Также
- Список фракталов по размерности Хаусдорфа
- Рог Габриэля (бесконечная площадь поверхности, но включает конечный объем)
- Кривая Госпера (также известная как Пеано– Кривая Госпера или поток змеи)
- Кривая Осгуда
- Самоподобие
- Терагон
- Функция Вейерштрасса
- Парадокс береговой линии
Ссылки
Дополнительная литература
- Каснер, Эдвард; Ньюман, Джеймс (2001) [1940]. «IX Изменчивость и изменчивость § Снежинка». Математика и воображение. Dover Press. С. 344–351. ISBN 0-486-41703-4 .
Внешние ссылки
| Внешнее видео |
|---|
|
| На Викискладе есть медиафайлы, связанные с Кривая Коха. |
- (2000) «Кривая фон Коха», компьютерной лабораторией efg в Wayback Machine (заархивировано 20 июля 2017 г.)
- Поэма Бернта Валя «Кривая Коха», Wahl.org. Проверено 23 сентября 2019 г.
- Вайсштейн, Эрик У. «Снежинка Коха». MathWorld. Проверено 23 сентября 2019 года.
- «7 итераций кривой Коха». Вольфрам Альфа Сайт. Проверено 23 сентября 2019 г.
- «Квадратные фрактальные кривые Коха». Демонстрационный проект Вольфрама. Проверено 23 сентября 2019 года.
- «Square Koch Fractal Surface». Демонстрационный проект Вольфрама. Проверено 23 сентября 2019 года.
- Применение кривой Коха к антенне
- Анимация WebGL, показывающая построение поверхности Коха, tchaumeny.github.io. Проверено 23 сентября 2019 г.
- «Математический анализ кривой Коха и квадратичной кривой Коха» (PDF). Архивировано из оригинального (pdf) 26 апреля 2012 г. Дата обращения 22 ноября 2011 г.
Многоугольник, изображенный на рисунке 5.12, а, называют снежинкой Коха. Постройте ее по следующему алгоритму:
⚫ начертите на листе нелинованной бумаги равносторонний треугольник со стороной 9 см (рис.5.12,б);
⚫ каждую сторону треугольника разделите на 3 равные части и на средней части постройте равносторонний треугольник (рис.5.12,в);
⚫ повторите это построение на каждой из 12 сторон получившегося многоугольника (рис.5.12,г);
⚫ чтобы получить снежинку, изображенную на рисунке 5.12,а, надо сделать еще один шаг построения.
Во сколько раз увеличивается число сторон снежинки Коха на каждом шаге построения? Во сколько раз при этом уменьшается длина ее стороны? Сколько сторон у снежинки, получаемой на каждом шаге? Чему равен ее периметр?
reshalka.com
ГДЗ учебник по математике 6 класс Дорофеев. 5.3 Построение треугольника. Номер №436
Решение
На каждом шаге построения число сторон снежинки увеличивается в 4 раза.
Длина стороны при этом уменьшается в 3 раза.
Число сторон снежинки:
1 шаг: 3 стороны;
2 шаг: 12 сторон;
3 шаг: 48 сторон.
Периметр снежинки:
1 шаг: 27 см;
2 шаг: 36 см;
3 шаг: 48 см.
Задание 305. Многоугольник, изображенный на рисунке 5.21, а, называют снежинкой Коха. Постройте ее. Для этого:
1) начертите на листе нелинованной бумаги равносторонний треугольник со стороной 9 см (рис. 5.21, б);
2) каждую сторону треугольника разделите на 3 равные части и на средней части постройте равносторонний треугольника (рис. 5.21, в);
3) повторите это построение на каждой из 12 сторон получившегося многоугольника (рис. 5.21, г);
4) чтобы получить снежинку, изображенную на рисунке 5.21, а, надо сделать еще один шаг построения.
Задание 306. ЗАДАЧА−ИССЛЕДОВАНИЕ
Во сколько раз увеличивается число сторон снежинки Коха на каждом шаге построения (см. рис. 5.21)? Во сколько раз при этом уменьшается длина ее стороны? Для каждого шага построения определите число сторон снежинки и ее периметр.
Решение
Число сторон снежинки Коха на каждом шаге построения увеличивается в 4 раза.
Шаг 1:
3 − число сторон;
9 (см) − длина стороны;
3 * 9 = 27 (см) − периметр.
Шаг 2:
3 * 4 = 12 − число сторон;
9 : 3 = 3 (см) − длина стороны;
12 * 3 = 36 (см) − периметр.
Шаг 3:
12 * 4 = 48 − число сторон;
3 : 3 = 1 (см) − длина стороны;
48 * 1 = 48 (см) − периметр.
Шаг 4:
48 * 4 = 192 − число сторон;
$1 : 3 = frac{1}{3}$ (см) − длина стороны;
$192 * frac{1}{3} = 64$ (см) − периметр.
Неравенство треугольника
Задание 307. 1) Убедитесь, что нельзя построить треугольник, стороны которого равны:
а) 7 см, 3 см и 3 см;
б) 6 см, 4 см и 2 см.
измените длину одной из сторон так, чтобы треугольник можно было построить.
2) Можно ли построить треугольник со сторонами:
а) 11 см, 13 см, 25 см;
б) 15 см, 6 см, 12 см;
в) 20 см, 18 см, 38 см?
Решение
1) а)
7 + 3 = 10 > 3;
7 + 3 = 10 > 3;
3 + 3 = 6 < 7 − значит, треугольник построить нельзя.
Увеличим одну из сторон, равную 3 см на 2 см, получим треугольник со сторонами: 7 см, 5 см, 3 см. Тогда:
7 + 5 = 12 > 3;
7 + 3 = 10 > 5;
3 + 5 = 8 > 7 − значит, треугольник построить можно.
б)
6 + 4 = 10 > 2;
6 + 2 = 8 > 4;
4 + 2 = 6 = 6 − значит, треугольник построить нельзя.
Увеличим сторону, равную 2 см на 1 см, получим треугольник со сторонами 6 см, 4 см, 3 см. Тогда:
4 + 3 = 7 > 6;
6 + 4 = 10 > 3;
6 + 3 = 9 > 4 − значит, треугольник построить можно.2) а)
11 + 25 = 36 > 13;
13 + 25 = 38 > 11;
11 + 13 = 24 < 25 − значит, треугольник построить нельзя.
б)
12 + 6 = 18 > 15;
12 + 15 = 27 > 6;
15 + 6 = 21 > 12 − значит, треугольник построить можно.
в)
20 + 38 = 58 > 18;
18 + 38 = 56 > 20;
20 + 18 = 38 = 38 − значит, треугольник построить нельзя.
Ответ:
а) нельзя;
б) можно;
в) нельзя.
Задание 308. В равнобедренным треугольнике одна сторона равна 7 см, а другая − 15 см. Какая сторона является основанием?
Решение
Пусть 15 см − основание, тогда:
7 (см) − вторая боковая сторона;
7 + 7 = 14 < 15, значит, основание не может быть 15 см.
Ответ: 7 см − основание.
Задание 309. Даны четыре отрезка длиной 2 см, 3 см, 5 см и 6 см. Сколько различных разносторонних треугольников можно построить из этих отрезков?
Решение
Вариант 1. Треугольник со сторонами 2 см, 3 см, 5 см.
2 + 5 = 7 > 3;
3 + 5 = 8 > 2;
2 + 3 = 5 = 5 − значит, треугольник построить нельзя.Вариант 2. Треугольник со сторонами 2 см, 5 см, 6 см.
2 + 5 = 7 > 6;
6 + 5 = 11 > 2;
2 + 6 = 8 > 5 − значит, треугольник построить можно.Вариант 3. Треугольник со сторонами 2 см, 3 см, 6 см.
2 + 6 = 8 > 3;
3 + 6 = 9 > 2;
2 + 3 = 5 < 6 − значит, треугольник построить нельзя.Вариант 4. Треугольник со сторонами 3 см, 5 см, 6 см.
3 + 5 = 8 > 6;
3 + 6 = 9 > 5;
5 + 6 = 11 > 3 − значит, треугольник построить можно.
Ответ: можно построить треугольники со сторонами:
2 см, 5 см, 6 см;
3 см, 5 см, 6 см.
Эта фигура — один из первых исследованных учеными фракталов. Она получается из трех копий кривой Коха, которая впервые появилась в статье шведского математика Хельге фон Коха в 1904 году. Эта кривая была придумана как пример непрерывной линии, к которой нельзя провести касательную ни в одной точке. Линии с таким свойством были известны и раньше (Карл Вейерштрасс построил свой пример еще в 1872 году), но кривая Коха замечательна простотой своей конструкции. Не случайно его статья называется «О непрерывной кривой без касательных, которая возникает из элементарной геометрии».
Рисунок и анимация отлично показывают, как по шагам строится кривая Коха. Первая итерация — просто начальный отрезок. Потом он делится на три равные части, центральная достраивается до правильного треугольника и затем выкидывается. Получается вторая итерация — ломаная линия, состоящая из четырех отрезков. К каждому из них применяется такая же операция, и получается четвертый шаг построения. Продолжая в том же духе, можно получать всё новые и новые линии (все они будут ломаными). А то, что получится в пределе (это уже будет воображаемый объект), и называется кривой Коха.
Основные свойства кривой Коха
1. Она непрерывна, но нигде не дифференцируема. Грубо говоря, именно для этого она и была придумана — как пример такого рода математических «уродцев».
2. Имеет бесконечную длину. Пусть длина исходного отрезка равна 1. На каждом шаге построения мы заменяем каждый из составляющих линию отрезков на ломаную, которая в 4/3 раза длиннее. Значит, и длина всей ломаной на каждом шаге умножается на 4/3: длина линии с номером n равна (4/3)n–1. Поэтому предельной линии ничего не остается, кроме как быть бесконечно длинной.
3. Снежинка Коха ограничивает конечную площадь. И это при том, что ее периметр бесконечен. Это свойство может показаться парадоксальным, но оно очевидно — снежинка полностью помещается в круг, поэтому ее площадь заведомо ограничена. Площадь можно посчитать, и для этого даже не нужно особых знаний — формулы площади треугольника и суммы геометрической прогрессии проходят в школе. Для интересующихся вычисление приведено ниже мелким шрифтом.
Пусть сторона исходного правильного треугольника равна a. Тогда его площадь . Сначала сторона равна 1, а площадь:
. Что происходит при увеличении итерации? Можно считать, что к уже имеющемуся многоугольнику пристраиваются маленькие равносторонние треугольнички. В первый раз их всего 3, а каждый следующий раз их в 4 раза больше чем было в предыдущий. То есть на n-м шаге будет достроено Tn = 3 · 4n–1 треугольничков. Длина стороны каждого из них составляет треть от стороны треугольника, достроенного на предыдущем шаге. Значит, она равна (1/3)n. Площади пропорциональны квадратам сторон, поэтому площадь каждого треугольничка равна
. При больших значениях n это, кстати, очень мало. Суммарный вклад этих треугольничков в площадь снежинки равен Tn · Sn = 3/4 · (4/9)n · S0. Поэтому после n-го шага площадь фигуры будет равна сумме S0 + T1 · S1 + T2 · S2 + … +Tn · Sn =
. Снежинка получается после бесконечного числа шагов, что соответствует n → ∞. Получается бесконечная сумма, но это сумма убывающей геометрической прогрессии, для нее есть формула:
. Площадь снежинки равна
.
4. Фрактальная размерность равна log4/log3 = log34 ≈ 1,261859… . Аккуратное вычисление потребует немалых усилий и подробных разъяснений, поэтому здесь приведена, скорее, иллюстрация определения фрактальной размерности. Из формулы степенной зависимости N(δ) ~ (1/δ)D, где N — число пересекающихся квадратиков, δ — их размер, а D — размерность, получаем, что D = log1/δN. Это равенство верно с точностью до прибавления константы (одной и той же для всех δ). На рисунках изображена пятая итерация построения кривой Коха, зеленым закрашены квадратики сетки, которые с ней пересекаются. Длина исходного отрезка равна 1, поэтому на верхнем рисунке длина стороны квадратиков равна 1/9. Закрашено 12 квадратиков, log912 ≈ 1,130929… . Пока не очень похоже на 1,261859… . Смотрим дальше. На среднем рисунке квадратики в два раза меньше, их размеры 1/18, закрашено 30. log1830 ≈ 1,176733… . Уже лучше. Внизу квадратики еще вдвое меньше, закрашено уже 72 штуки. log7230 ≈ 1,193426… . Еще ближе. Дальше нужно увеличивать номер итерации и одновременно уменьшать квадратики, тогда «эмпирическое» значение размерности кривой Коха будет неуклонно приближаться к log34, а в пределе и вовсе совпадет.
Варианты
Снежинка Коха «наоборот» получается, если строить кривые Коха внутрь исходного равностороннего треугольника.
Линии Чезаро. Вместо равносторонних треугольников используются равнобедренные с углом при основании от 60° до 90°. На рисунке угол равен 88°.
Квадратный вариант. Тут достраиваются квадраты.
Трехмерные аналоги. Пирамида Коха.
Далее: Т-квадрат
























