Сторона основания пирамиды является стороной правильного многоугольника, исходя из этого, можно найти все параметры пирамиды, связанные с основанием, воспользовавшись формулами для правильных многоугольников.
P=n(a+b)
S=(na^2)/(4 tan〖(180°)/n〗 )
Чтобы найти радиус окружности, вписанной в основание правильной пирамиды, нужно разделить сторону основания на два тангенса из 180 градусов, деленных на количество сторон в основании. (рис.34.1)
r=a/(2 tan〖(180°)/n〗 )
Радиус окружности, описанной вокруг основания правильной пирамиды, равен отношению стороны основания к двум синусам того же угла. (рис.34.2)
R=a/(2 sin〖(180°)/n〗 )
Угол γ между сторонами правильного многоугольника, заложенного в основание пирамиды, легко найти, умножив 180 градусов на количество сторон многоугольника без двух, и деленное на полное количество сторон. (рис.34.3)
γ=180°(n-2)/n
Зная боковое ребро в совокупности со стороной основания, можно вычислить высоту пирамиды и ее апофему из прямоугольных треугольников, которые они образуют. (рис.34.5, 35.1)
h=√(b^2-R^2 )=√(b^2-(a/(2 sin〖(180°)/n〗 ))^2 )
l=√(b^2-a^2/4)
Косинус угла между боковым ребром и основанием будет равен отношению радиуса окружности, описанной вокруг основания, к боковому ребру пирамиды, а косинус угла между апофемой и основанием – отношению радиуса вписанной в основание окружности к апофеме. (рис.34.4,34.5)
cosα=R/b=a/(2b sin〖(180°)/n〗 )
cosβ=r/l=a/(2 tan〖(180°)/n〗 √(b^2-a^2/4))
Площадь боковой поверхности пирамиды складывается из площадей треугольников, являющихся ее гранями, каждая из которых равна половине произведения апофемы на сторону основания, а площадь полной поверхности представляет собой сумму площади боковой поверхности и площади основания.
S_(б.п.)=lan/2=(√(b^2-a^2/4) an)/2
S_(п.п.)=an(l/2+a/(4 tan〖(180°)/n〗 ))=an(√(b^2-a^2/4)/2+a/(4 tan〖(180°)/n〗 ))
Чтобы найти объем пирамиды, необходимо вычислить треть от произведения ее высоты на площадь основания, последовательно подставив выражения для площади и высоты в формулу.
V=1/3 S_(осн.) h=(na^2 √(b^2-(a/(2 sin〖(180°)/n〗 ))^2 ))/(12 tan〖(180°)/n〗 )
Радиус сферы, которая может быть вписана в пирамиду, равен трем объемам, деленным на площадь полной поверхности пирамиды, а радиус сферы, описанной вокруг пирамиды – квадрату бокового ребра, деленному на две высоты. (рис.34.6,34.7)
r_1=3V/S_(п.п.) =(a√(b^2-(a/(2 sin〖(180°)/n〗 ))^2 ))/(tan〖(180°)/n〗 (2√(b^2-a^2/4)+a/tan〖(180°)/n〗 ) )
R_1=b^2/2h=b^2/(2√(b^2-(a/(2 sin〖(180°)/n〗 ))^2 ))
Площадь поверхности правильной пирамиды формулы и калькулятор
{S_{полн} = dfrac{1}{2}PL + S}
Найти площадь
полной поверхностибоковой поверхности
Тип пирамиды
правильнаяправильная треугольнаяправильная четырехугольнаяправильная шестиугольная
Через
периметр, площадь и апофемусторону основания и высоту
Периметр основания P
ммсмдммкмдюймы (in)футы (ft)
Апофема L
ммсмдммкмдюймы (in)футы (ft)
Площадь основания S
мм²см²дм²м²км²кв. дюймы (in²)кв. футы (ft²)
Результат в
мм²см²дм²м²км²кв. дюймы (in²)кв. футы (ft²)
Виджет
Ссылка на расчет
Сообщить об ошибке
Сохранить расчет
Печатать
На странице вы найдете онлайн-калькуляторы, которые помогут найти площадь полной и боковой поверхности правильной пирамиды, а также треугольной, четырехугольной и шестиугольной пирамиды. Кроме того приводятся формулы, по которым вы можете произвести расчет самостоятельно.
- калькулятор площади поверхности пирамиды
- формула площади полной поверхности правильной пирамиды через периметр, площадь и апофему
- формула площади полной поверхности правильной пирамиды через сторону основания и высоту
- формула площади полной поверхности правильной треугольной пирамиды через сторону основания и апофему
- формула площади полной поверхности правильной треугольной пирамиды через сторону основания и боковую грань
- формула площади полной поверхности правильной треугольной пирамиды через сторону основания и высоту
- формула площади полной поверхности правильной четырехугольной пирамиды через сторону и боковую грань
- формула площади полной поверхности правильной четырехугольной пирамиды через сторону и высоту
- формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и апофему
- формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и апофему
- формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
- формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной пирамиды через периметр и апофему
- формула площади боковой поверхности правильной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и апофему
- формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и боковую грань
- формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной треугольной пирамиды через периметр основания и апофему
- формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и апофему
- формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и боковую грань
- формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и апофему
- формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
- формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и высоту
- примеры задач
Познакомьтесь с важными понятиями, которые необходимо знать для расчета площади поверхности пирамиды.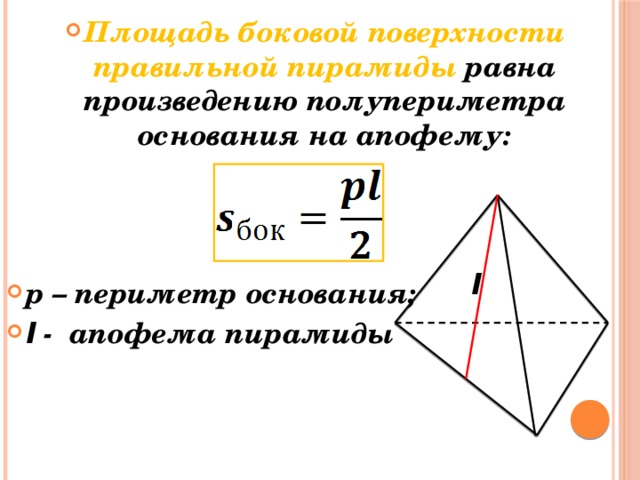
Пирамида — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину.
Правильная пирамида – это пирамида, основанием которой является правильный многоугольник, а вершина фигуры проецируется в центр ее основания.
Площадь полной поверхности пирамиды — это сумма площадей боковых граней и площади основания.
Площадь боковой поверхности пирамиды — это совокупная площадь всех боковых граней пирамиды.
Апофема — перпендикуляр, опущенный из вершины пирамиды на ребро основания.
Формула площади полной поверхности правильной пирамиды через периметр, площадь и апофему
{S_{полн} = dfrac{1}{2}PL+S}
P — периметр основания пирамиды
L — апофема пирамиды
S — площадь основания пирамиды
Формула площади полной поверхности правильной пирамиды через сторону основания и высоту
{S_{полн} = dfrac{na}{2} {Bigg( dfrac{a}{2 \tg ( dfrac{180°}{n})} + sqrt{h^2+ Bigg( dfrac{a}{2 \tg ( dfrac{180°}{n})} Bigg) ^2} Bigg)}}
a — сторона основания пирамиды
h — высота пирамиды
n — число сторон основания
Формула площади полной поверхности правильной треугольной пирамиды через сторону основания и апофему
{S_{полн} = dfrac{a^2 sqrt{3}+6aL}{4}}
a — сторона основания пирамиды
L — апофема пирамиды
Формула площади полной поверхности правильной треугольной пирамиды через сторону основания и боковую грань
{S_{полн} = dfrac{a^2 sqrt{3}+6a sqrt{b^2 — dfrac{a^2}{4}}}{4}}
a — сторона основания пирамиды
b — боковая грань пирамиды
Формула площади полной поверхности правильной треугольной пирамиды через сторону основания и высоту
{S_{полн} = dfrac{3a}{2} {Bigg( dfrac{a}{2 tg ( 60°)} + sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 60°)} Bigg) ^2} Bigg)}}
a — сторона основания пирамиды
h — высота пирамиды
Формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и боковую грань
{S_{полн} = a^2 + 2a sqrt{b^2- dfrac{a^2}{4}}}
a — сторона основания пирамиды
b — боковая грань пирамиды
Формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и высоту
{S_{полн} = 2a {Bigg( dfrac{a}{2 tg ( 45°)} + sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 45°)} Bigg) ^2} Bigg)}}
a — сторона основания пирамиды
h — высота пирамиды
Формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и апофему
{S_{полн} = a^2+2aL}
a — сторона основания пирамиды
L — апофема пирамиды
Формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и апофему
{S_{полн} = dfrac{3sqrt{3}a^2}{2}+3aL}
a — сторона основания пирамиды
L — апофема пирамиды
Формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
{S_{полн} = dfrac{3sqrt{3}a^2}{2}+3asqrt{b^2-dfrac{a^2}{4}}}
a — сторона основания пирамиды
b — боковая грань пирамиды
Формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и высоту
{S_{полн} = 3a {Bigg( dfrac{a}{2 tg ( 30°)} + sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 30°)} Bigg) ^2} Bigg)}}
a — сторона основания пирамиды
h — высота пирамиды
Формула площади боковой поверхности правильной пирамиды через периметр и апофему
{S_{бок} = dfrac{1}{2}PL}
P — периметр основания пирамиды
L — апофема пирамиды
Формула площади боковой поверхности правильной пирамиды через сторону основания и высоту
{S_{бок} = dfrac{na}{2} sqrt{h^2+ Bigg( dfrac{a}{2 tg ( dfrac{180°}{n})} Bigg) ^2} }
a — сторона основания пирамиды
h — высота пирамиды
n — число сторон основания
Формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и апофему
{S_{бок} = dfrac{3}{2}aL}
a — сторона основания пирамиды
L — апофема пирамиды
Формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и боковую грань
{S_{бок} = dfrac{3a sqrt{b^2 — dfrac{a^2}{4}}}{2}}
a — сторона основания пирамиды
b — боковая грань пирамиды
Формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и высоту
{S_{бок} = dfrac{3a}{2} sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 60°)} Bigg) ^2}}
a — сторона основания пирамиды
h — высота пирамиды
Формула площади боковой поверхности правильной треугольной пирамиды через периметр основания и апофему
{S_{бок} =dfrac{1}{2}PL}
P — периметр основания пирамиды
L — апофема пирамиды
Формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и апофему
{S_{бок} = 2aL}
a — сторона основания пирамиды
L — апофема пирамиды
Формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и боковую грань
{S_{бок} = 2a sqrt{b^2 — dfrac{a^2}{4}}}
a — сторона основания пирамиды
b — боковая грань пирамиды
Формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и высоту
{S_{бок} = 2a sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 45°)} Bigg) ^2}}
a — сторона основания пирамиды
h — высота пирамиды
Формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и апофему
{S_{бок} = 3aL}
a — сторона основания пирамиды
L — апофема пирамиды
Формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
{S_{бок} = 3asqrt{b^2-dfrac{a^2}{4}}}
a — сторона основания пирамиды
b — боковая грань пирамиды
Формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и высоту
{S_{бок} = 3a sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 30°)} Bigg) ^2}}
a — сторона основания пирамиды
h — высота пирамиды
Примеры задач на нахождение площади поверхности пирамиды
Задача 1
Стороны основания правильной четырехугольной пирамиды равны 60см, боковые ребра равны 78см.
2} = 60 : см²
Ответ: 60 см²
Проверка .
Геометрия 10-11 класс. Пирамида — math200.ru
Skip to content
Геометрия 10-11 класс. Пирамидаadmin2022-11-30T21:50:23+03:00
Скачать файл в формате pdf.
Геометрия 10-11 класс. Пирамида
Пирамидой называется многогранник, который состоит из плоского многоугольника – основания пирамиды, точки, не лежащей в плоскости основания,– вершины пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания. Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами. Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания. Пирамида называется n-угольной, если ее основанием является n-угольник. Треугольная пирамида называется также тетраэдром.
Пирамида называется правильной, если ее основанием является правильный многоугольник, а основание высоты совпадает с центром этого многоугольника. Очевидно, у правильной пирамиды боковые ребра равны; следовательно, боковые грани – равные равнобедренные треугольники. Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой.
Площадь боковой поверхности правильной пирамиды вычисляется по формуле:({S_{{text{бок}}{text{.пов}}}} = frac{1}{2}p,l), где p – периметр основания; l – длина апофемы.
Объем пирамиды вычисляется по формуле: (V = frac{1}{3}S,H), где S – площадь основания; H – длина высоты пирамиды.
Если у пирамиды все боковые ребра равны между собой или наклонены под одним и тем же углом к плоскости основания, то основание высоты пирамиды совпадает с центром окружности, описанной около основания пирамиды (эта же точка служит точкой пересечения серединных перпендикуляров к сторонам основания пирамиды).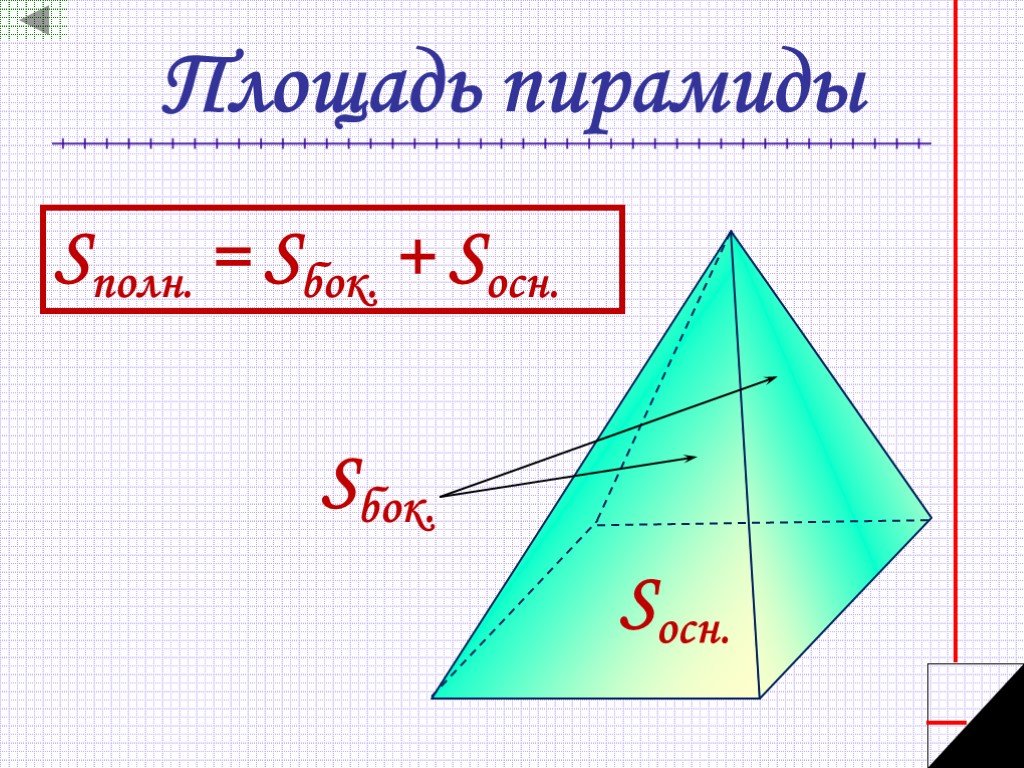
Если у пирамиды боковые грани наклонены к плоскости основания под одним и тем же углом, то основание высоты пирамиды совпадает с центром окружности, вписанной в основание (эта же точка служит точкой пересечения биссектрис углов в основании пирамиды).
Задачи для самостоятельного решения
| Задача 1. Стороны основания треугольной пирамиды равны 5, 8 и 9. Высоты боковых граней, проведенных к ребрам основания равны 10. Найдите площадь боковой поверхности пирамиды.
Ответ ОТВЕТ: 110. |
| Задача 2. Дана правильная семиугольная пирамида, ребро основания равно 8, апофема – 9. Найдите площадь боковой поверхности пирамиды.
Ответ ОТВЕТ: 252. |
| Задача 3. Периметр основания правильной четырехугольной пирамиды – 32, апофема – 7. Найдите площадь одной боковой грани.
Ответ ОТВЕТ: 28. |
Задача 4. Дана треугольная пирамида DABC.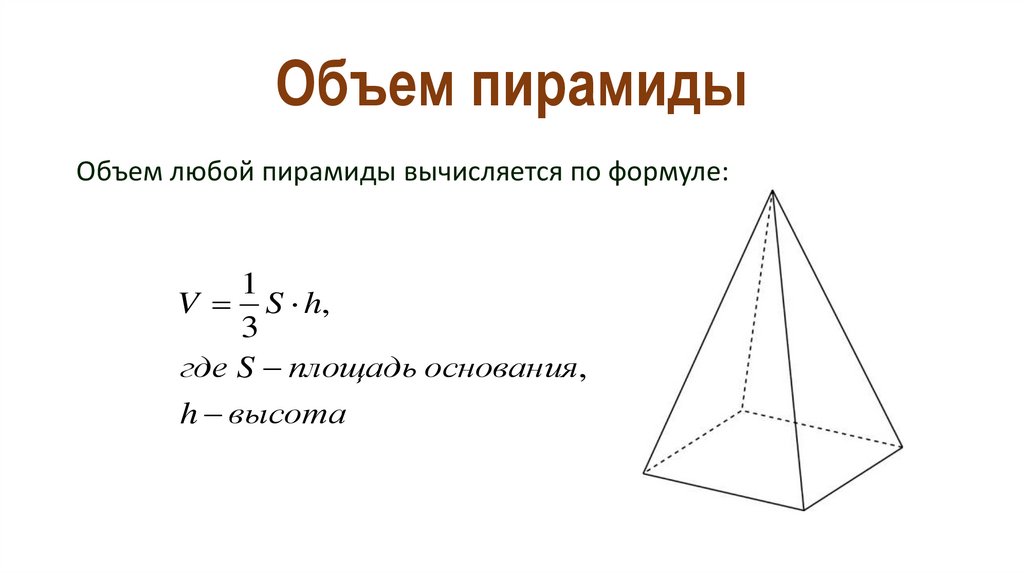 Боковые ребра DA = DB = DC = 5, AB = AC = 8, BC = 6. Найдите площадь боковой поверхности.
Ответ ОТВЕТ: 36. |
| Задача 5. Дана правильная четырехугольная пирамида, её высота равна 3, площадь боковой поверхности 80. Найдите площадь полной поверхности.
Ответ ОТВЕТ: 144. |
| Задача 6. Высоты боковых граней четырехугольной пирамиды, проведенные из вершины равны 7, две противоположные стороны основания равны 8 и 14. Найдите площадь боковой поверхности.
Ответ ОТВЕТ: 154. |
| Задача 7. Дана правильная четырехугольная пирамида с боковыми ребрами равными 10 и высотой – (2sqrt 7 .) Найдите площадь полной поверхности пирамиды.
Ответ ОТВЕТ: 336. |
Задача 8. Дана четырехугольная пирамида SABCD, в основании которой равнобедренная трапеция в которую можно вписать окружность с основаниями AB = 9 и CD = 4. circ }.) Найдите площадь полной поверхности пирамиды.
Ответ ОТВЕТ: 117. |
| Задача 9. Дана треугольная пирамида SABC с высотой SA, равной 9. Стороны основания AB = AC = 13, BC = 10. Найдите площадь полной поверхности пирамиды.
Ответ ОТВЕТ: 252. |
| Задача 10. Дана четырехугольная пирамида SABCD в основании, которой ромб ABCD с диагоналями AC = 16, BD = 12 которые пересекаются в точке O. Отрезок SO равный 2 является высотой пирамиды. Найдите площадь боковой поверхности.
Ответ ОТВЕТ: 104. |
Задача 11. Дана четырехугольная пирамида SABCD в основании, которой ромб ABCD площадь которого равна 60 и стороной 10. Диагонали ромба пересекаются в точке O. Отрезок SO равный 4 является высотой пирамиды. Найдите площадь боковой поверхности.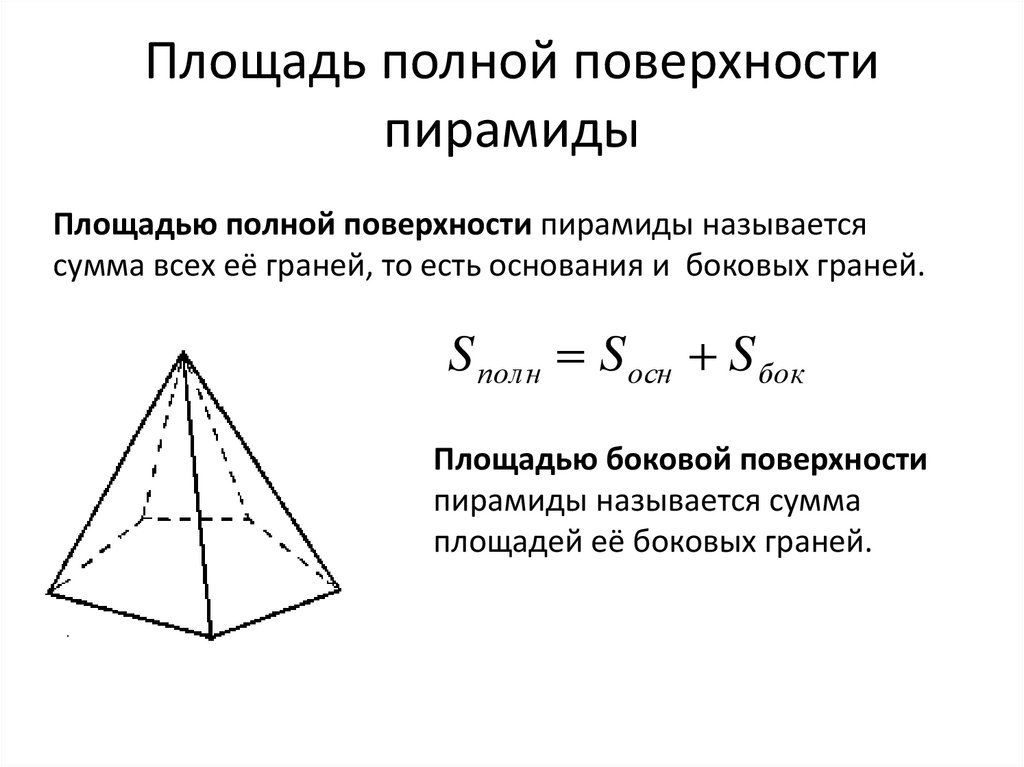 circ }.) Найдите высоту пирамиды.
Ответ ОТВЕТ: 5. |
Реклама
Поддержать нас
пирамид
пирамид
Показать рекламу
Скрыть рекламу
О рекламе
Когда мы думаем о пирамидах, мы думаем о Великих пирамидах Египта .
На самом деле это Квадратные пирамиды , потому что их основание — Квадрат.
Части пирамиды
Пирамида получается путем соединения основания с вершиной
Основание представляет собой многоугольник (плоский с прямыми краями), а все остальные грани — треугольники. Никаких кривых!
Типы пирамид
Существует много типов пирамид, и они названы в честь формы их основания.
| Пирамида | База | |
| Треугольный Пирамида: |
||
|---|---|---|
| Квадрат Пирамида: |
||
| Пятиугольный Пирамида: |
||
| .  .. и так далее … |
Пролетите здесь через несколько пирамид.
Правая и наклонная пирамида
Это говорит нам, где вершина (вершина) пирамиды. Когда вершина находится прямо над центром основания, это правильная пирамида , в противном случае это наклонная пирамида .
| Правая пирамида | Наклонная пирамида |
|---|
Правильная и неправильная пирамида
Это говорит нам о форме основания . Когда основание представляет собой правильный многоугольник, это правильная пирамида , иначе это неправильная пирамида .
| Правильная пирамида | Неправильная пирамида |
|---|---|
| Основание стандартное | Основание неправильной формы |
Площадь и объем
Объем пирамиды
- 1 / 3 × [Площадь основания] × Высота
Площадь поверхности пирамиды
Когда все боковые грани одинаковы:
- [Площадь основания] +
1 / 2 × периметр × [наклонная длина]
Если боковые грани разные:
- [Основная площадь] + [Боковая площадь]
Примечания по площади поверхности
Площадь поверхности состоит из двух частей: площадь основания ( Базовая площадь ) и площадь боковых граней ( Боковая площадь ).
Для Базовая площадь :
Это зависит от формы, существуют разные формулы для треугольника, квадрата и т. д. Формулы см. в разделе Площадь или в нашем Инструменте расчета площади
Для Боковая площадь :
Когда все боковые грани одинаковые:
- Умножьте периметр на «наклонную длину» и разделите на 2. Это потому, что боковые грани всегда являются треугольниками, а треугольник формула «база умноженная на высоту, деленная на 2»
Но когда боковые грани разные (например, в «неправильной» пирамиде), мы должны сложить площади каждого треугольника, чтобы найти общую боковую площадь.
Copyright © 2017 MathsIsFun.com
Как найти площадь боковой поверхности квадратной пирамиды
Обновлено 25 февраля 2023 г.
Клэр Гиллеспи
Математические задачи с трехмерными фигурами могут потребовать от нас найти площадь боковой поверхности квадратной пирамиды.
Площадь боковой поверхности – это сумма площадей его боковых граней (боков), а площадь полной поверхности – сумма его боковых граней и основания. Таким образом, в квадратной пирамиде боковые грани — это четыре треугольника, которые образуют верхнюю и боковые части фигуры.
TL;DR (слишком длинно, не читал)
Во всех следующих вычислениях мы предполагаем, что это правильные пирамиды. Это означает, что вершина пирамиды находится прямо над центром основания. Это означает, что все боковые стороны являются равнобедренными треугольниками (или равносторонними).
Решение для площади боковой поверхности
Общая формула площади боковой поверхности правильной пирамиды:
text{площадь боковой поверхности} = 2 times text{периметр основания} times text{высота наклона пирамиды}
Эта формула по существу находит площадь, которая составляет каждую боковую грань, по классической формуле площади треугольника:
text{Площадь} = text{база} times text{высота}
периметр действует как совокупное основание для всех сторон, а наклонная высота пирамиды является высотой треугольников.
Затем мы делим на два, чтобы учесть площадь треугольника, и получаем формулу площади поверхности.
Определение боковой поверхности
Вычислите периметр основания, умножив длину стороны пирамиды на четыре, потому что у квадрата четыре равные стороны. Найти наклонную высоту одной из боковых граней может оказаться сложнее, но в реальном мире ее часто можно измерить с помощью довольно простых инструментов.
Если сторона квадратной пирамиды – прямоугольной пирамиды с квадратным основанием – равна 6 дюймам, периметр равен:
4 х 6 = 24 text{ дюймов}
Боковой наклон квадратной пирамиды расстояние от вершины пирамиды до края основания, делящего пополам одну из граней треугольника. Если высота поперечного наклона составляет 8 дюймов, мы можем вычислить
24 х 8 = 192
-
. Если вместо этого нам дана высота квадратной пирамиды, мы можем использовать теорему Пифагора, чтобы найти наклонную высоту.
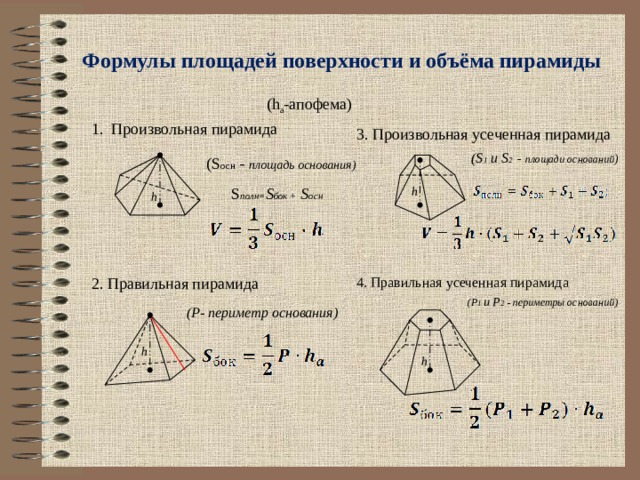Просто будьте осторожны, чтобы использовать основание прямоугольного треугольника в пределах размеров квадратной пирамиды.
Разделите ваш ответ на два
Чтобы найти площадь боковой поверхности, мы вычисляем
Теперь мы знаем, что площадь боковой поверхности квадратной пирамиды с периметром основания 24 дюйма и высотой бокового наклона 8 дюймов составляет 96 квадратных дюймов.
-
Если мы уже знаем площадь каждой из четырех боковых граней квадратной пирамиды, мы можем вычислить площадь боковой поверхности, найдя сумму площадей боковых граней. Например, если площади боковых граней составляют 10 дюймов, 10 дюймов, 7 дюймов и 7 дюймов, получится 10 + 10 + 7 + 7 = 34. Площадь боковой поверхности составляет 34 квадратных дюйма. 92
Боковая площадь прямоугольной пирамиды
Прямоугольная пирамида представляет другой уровень сложности при нахождении боковой площади, но мы по-прежнему можем использовать те же принципы, что и для пирамиды с квадратным основанием.
Поскольку прямоугольная пирамида по-прежнему имеет треугольные стороны, мы можем использовать формулу площади треугольника, но нам нужно учитывать, что стороны прямоугольника различны. Это означает, что равными будут только треугольники напротив друг друга, а не все четыре боковые грани. Чтобы учесть это, мы можем вычислить боковую площадь в парах противоположных граней, поэтому мы разобьем периметр на длину (l) и ширину (w) и их боковые грани.
A_text{lateral} = frac{2l times h_{длина} + 2w times h_{ширина}}{2}
Применение этих взаимосвязей к другим пирамидам
многоугольник, отличный от квадрата, эта формула для площади поперечного сечения все еще может быть применена. Будь то шестиугольная пирамида (с 6 боковыми сторонами) или пятиугольная пирамида (с 5 боковыми сторонами), можно использовать общую формулу в начале. Поскольку все пирамиды имеют треугольные грани, мы можем вычислить периметр, просуммировав стороны основания, а затем умножив периметр на высоту наклона и разделив его на два, чтобы получить площадь поперечного сечения.
Как найти сторону основания пирамиды
Задачи на вычисление стороны основания пирамиды составляют в задачнике по геометрии довольно большой раздел. Очень многое зависит от того, какая гемоетрическая фигура лежит в основании, а также от того, что дано в условиях задачи.
Вам понадобится
- – чертежные принадлежности;
- – тетрадь в клетку;
- – теорема синусов;
- – теорема Пифагора;
- – калькулятор.
Инструкция
В школьном курсе геометрии рассматриваются главным образом пирамиды, в основании которых лежит правильный многоугольник, то есть такой, у которого все стороны равны. Проекция вершины пирамиды совпадает с центром ее основания. Начертите пирамиду, в основании которой лежит равносторонний треугольник. В условиях могут быть даны:
– длина бокового ребра пирамиды и угол его с ребром между боковой гранью и основанием;
– длина бокового ребра и высота боковой грани;
– длина бокового ребра и высота пирамиды.
Если известны боковое ребро и угол, задача решается несколько иначе. Вспомните, что собой представляет каждая боковая грань пирамиды, в основании которой лежит равносторонний многоугольник. Это равнобедренный треугольник. Проведите его высоту, которая одновременно является биссектрисой и медианой. То есть половина стороны основания a/2=L*cosA, где а – сторона основания пирамиды, L – длина ребра. Чтобы найти размер стороны основания, достаточно полученный результат умножить на 2.
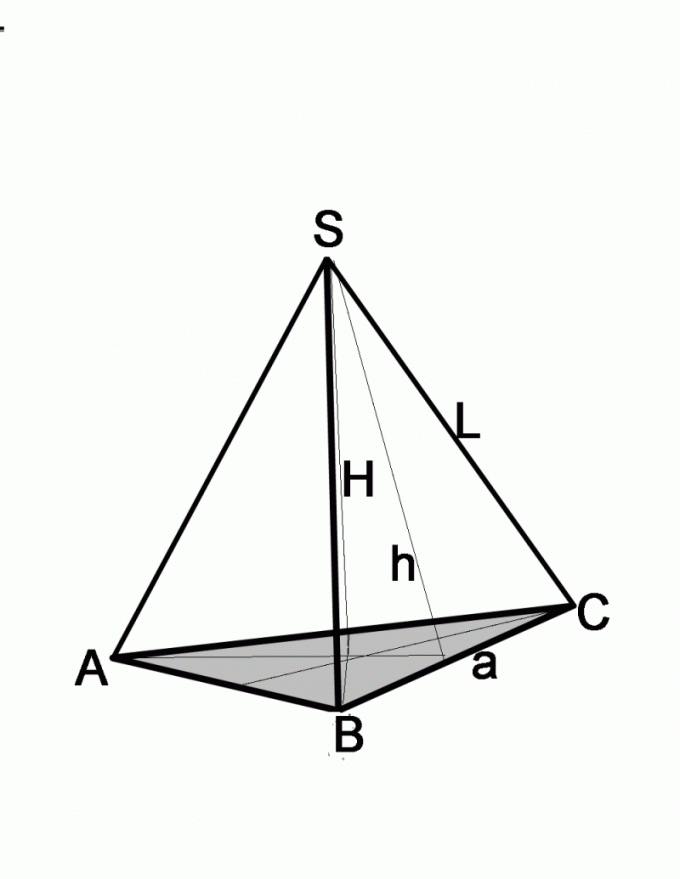
Если в задаче даны высота боковой грани и длина ребра, найдите сторону основания по теореме Пифагора. Боковая грань в данном случае будет гипотенузой, известная высота –з одним из катетов. Чтобы найти длину второго катета, нужно из квадрата гипотенузы вычесть квадрат второго катета, то есть (a/2)2=L2-h2, где а – сторона основания, L – длина боковой грани, h – высота боковой грани.
В этом случае нужно выполнить дополнительное построение, чтобы можно было оперировать тригонометрическими функциями. Вам даны боковое ребро L и высота пирамиды H, которая соединяет вершину пирамиды с центром основания. Из точки пересечения высоты с плоскостью основания проведите отрезок, соединив эту точку с одним из углов основания. У вас получился прямоугольный треугольник, гипотенузой которого является боковое ребро, одним из катетов – высота пирамиды. По этим данным легко найти второй катет треугольника, для этого достаточно из квадрата бокового ребра L вычесть квадрат высоты H. Дальнейшие действия зависят от того, какая именно фигура лежит в основании.
Вспомните свойства равностороннего треугольника. У него высоты одновременно являются биссектрисами и медианами. В точке пересечения они делятся пополам. То есть получается, что вы нашли половину высоты основания. Для удобства вычислений проведите все три высоты. Вы увидите, что отрезок, квадрат длины которого вы уже нашли, является гипотенузой прямоугольного треугольника. Извлеките квадратный корень. Вам известен и острый угол – 30°, так что найти половину стороны основания не составит особого труда, применив теорему косинусов.
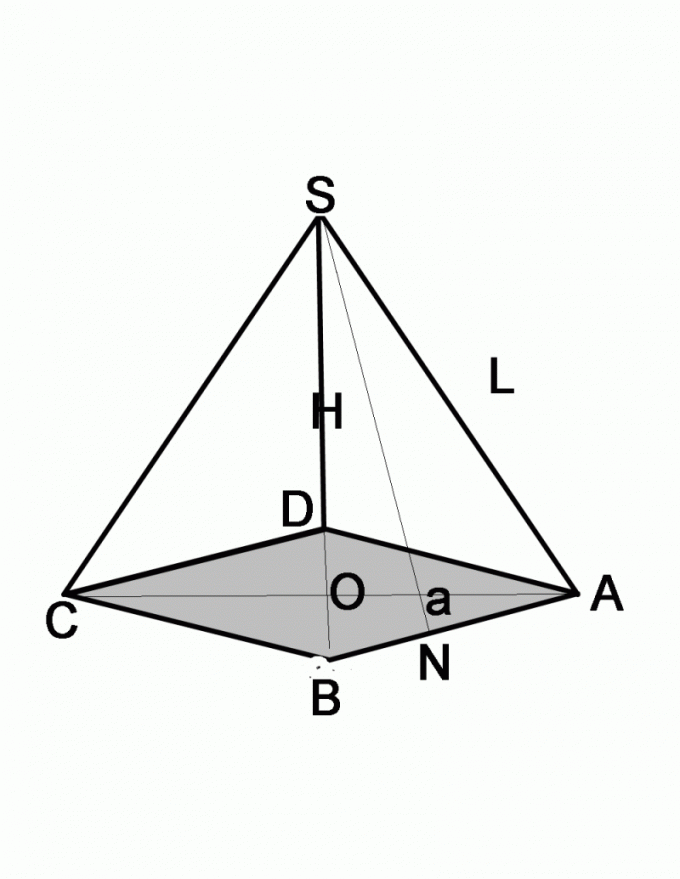
Для пирамиды, в основании которой лежит правильный четырехугольник, алгоритм будет тем же самым. Если вы вычтите из квадрата бокового ребра квадрат высоты пирамиды, получите возведенную в квадрат половину диагонали основания. Извлеките корень, найдите размер диагонали, которая одновременно является гипотенузой равнобедренного прямоугольного треугольника. Размер любого из катетов найдите по теореме Пифагора, синусов или косинусов.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Формулы и свойства правильной треугольной пирамиды. Усеченная треугольная пирамида
Объемной фигурой, которая часто появляется в геометрических задачах, является пирамида. Самая простая из всех фигур этого класса – треугольная. В данной статье разберем подробно основные формулы и свойства правильной пирамиды треугольной.
Геометрические представления о фигуре
Прежде чем переходить к рассмотрению свойств правильной пирамиды треугольной, разберемся подробнее, о какой фигуре идет речь.
Предположим, что имеется произвольный треугольник в трехмерном пространстве. Выберем в этом пространстве любую точку, которая в плоскости треугольника не лежит, и соединим ее с тремя вершинами треугольника. Мы получили треугольную пирамиду.
Вам будет интересно: Лихой – это: значение и синонимы
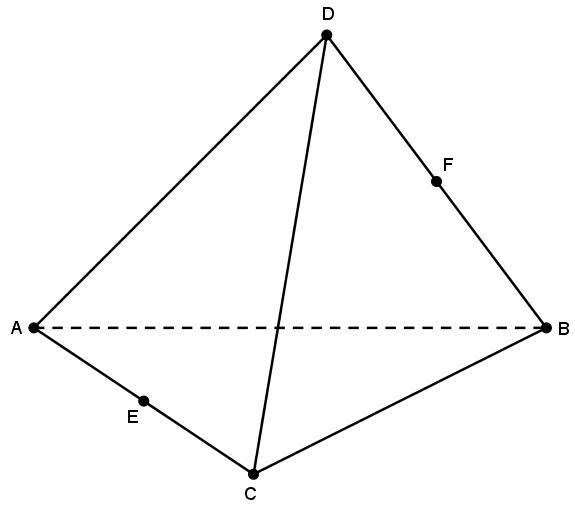
Она состоит из 4-х сторон, причем все они являются треугольниками. Точки, в которых соединяются три грани, называются вершинами. Их у фигуры также четыре. Линии пересечения двух граней – это ребра. Ребер у рассматриваемой пирамиды 6. Рисунок ниже демонстрирует пример этой фигуры.
Поскольку фигура образована четырьмя сторонами, ее также называют тетраэдром.
Правильная пирамида
Выше была рассмотрена произвольная фигура с треугольным основанием. Теперь предположим, что мы провели перпендикулярный отрезок из вершины пирамиды к ее основанию. Этот отрезок называется высотой. Очевидно, что можно провести 4 разные высоты для фигуры. Если высота пересекает в геометрическом центре треугольное основание, то такая пирамида называется прямой.
Прямая пирамида, основанием которой будет треугольник равносторонний, называется правильной. Для нее все три треугольника, образующих боковую поверхность фигуры, являются равнобедренными и равны друг другу. Частным случаем правильной пирамиды является ситуация, когда все четыре стороны являются равносторонними одинаковыми треугольниками.
Рассмотрим свойства правильной пирамиды треугольной и приведем соответствующие формулы для вычисления ее параметров.
Сторона основания, высота, боковое ребро и апотема
Любые два из перечисленных параметров однозначно определяют остальные две характеристики. Приведем формулы, которые связывают названные величины.
Предположим, что сторона основания треугольной пирамиды правильной равна a. Длина ее бокового ребра равна b. Чему будут равны высота правильной пирамиды треугольной и ее апотема.
Для высоты h получаем выражение:
Эта формула следует из теоремы Пифагора для прямоугольного треугольника, сторонами которого являются боковое ребро, высота и 2/3 высоты основания.
Апотемой пирамиды называется высота для любого бокового треугольника. Длина апотемы ab равна:
Из этих формул видно, что какими бы ни были сторона основания пирамиды треугольной правильной и длина ее бокового ребра, апотема всегда будет больше высоты пирамиды.
Представленные две формулы содержат все четыре линейные характеристики рассматриваемой фигуры. Поэтому по известным двум из них можно найти остальные, решая систему из записанных равенств.
Объем фигуры
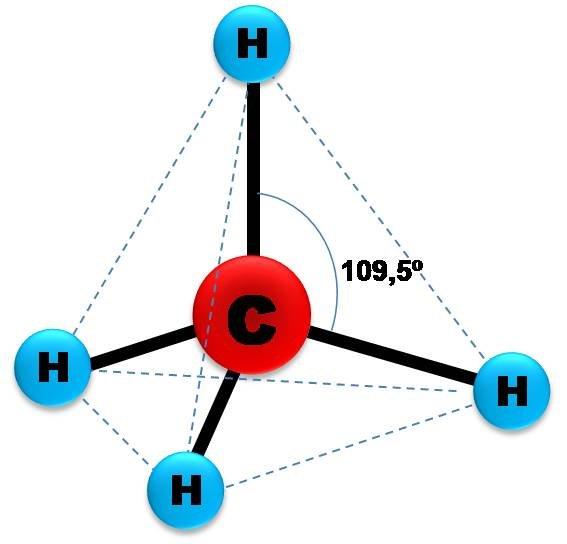
Для абсолютно любой пирамиды (в том числе наклонной) значение объема пространства, ограниченного ею, можно определить, зная высоту фигуры и площадь ее основания. Соответствующая формула имеет вид:
Применяя это выражение для рассматриваемой фигуры, получим следующую формулу:
Где высота правильной треугольной пирамиды равна h, а ее сторона основания – a.
Не сложно получить формулу для объема тетраэдра, у которого все стороны равны между собой и представляют равносторонние треугольники. В таком случае объем фигуры определится по формуле:
То есть он определяется длиной стороны a однозначно.
Площадь поверхности
Продолжим рассматривать свойства пирамиды треугольной правильной. Общая площадь всех граней фигуры называется площадью ее поверхности. Последнюю удобно изучать, рассматривая соответствующую развертку. На рисунке ниже показано, как выглядит развертка правильной пирамиды треугольной.
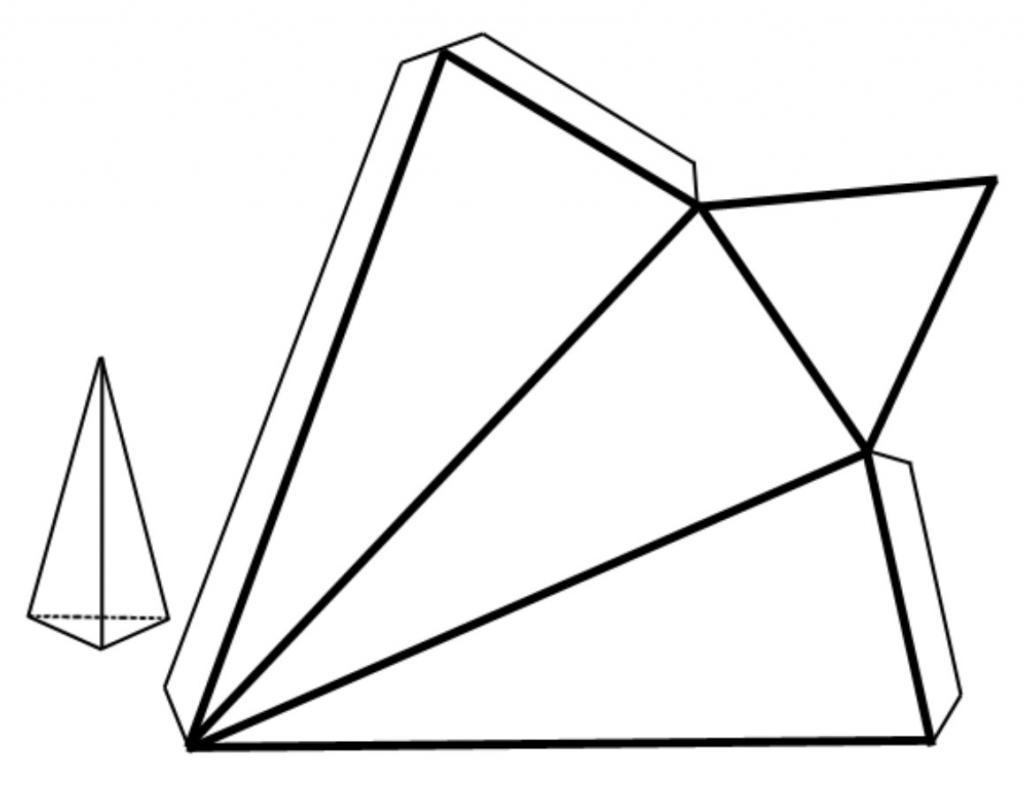
Предположим, что нам известны высота h и сторона основания a фигуры. Тогда площадь ее основания будет равна:
Получить это выражение может каждый школьник, если вспомнит, как находить площадь треугольника, а также учтет, что высота равностороннего треугольника также является биссектрисой и медианой.
Площадь боковой поверхности, образованной тремя одинаковыми равнобедренными треугольниками, составляет:
Данное равенство следует из выражения апотемы пирамиды через высоту и длину основания.
Полная площадь поверхности фигуры равна:
S = So + Sb = √3/4*a2 + 3/2*√(a2/12+h2)*a
Заметим, что для тетраэдра, у которого все четыре стороны являются одинаковыми равносторонними треугольниками, площадь S будет равна:
Свойства правильной усеченной пирамиды треугольной
Если у рассмотренной треугольной пирамиды плоскостью, параллельной основанию, срезать верх, то оставшаяся нижняя часть будет называться усеченной пирамидой.
В случае правильной пирамиды с треугольным основанием в результате описанного метода сечения получается новый треугольник, который также является равносторонним, но имеет меньшую длину стороны, чем сторона основания. Усеченная треугольная пирамида показана ниже.
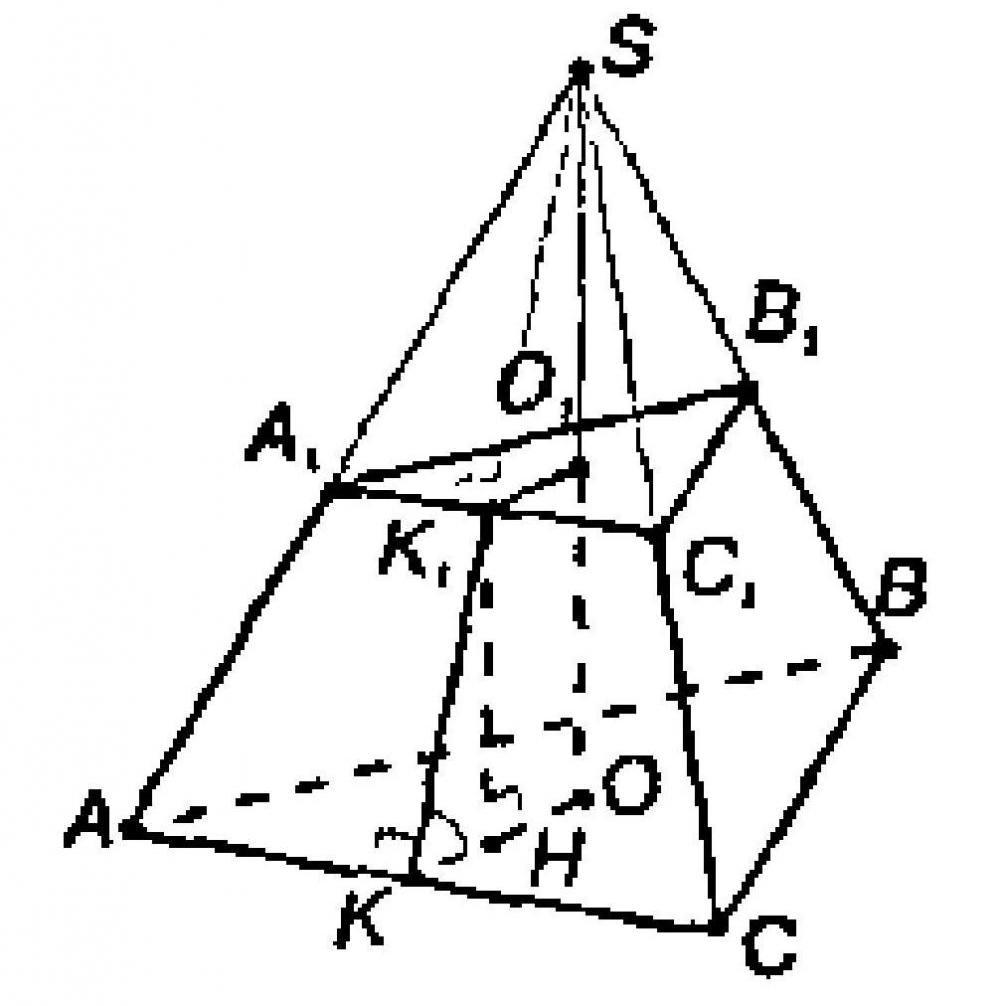
Мы видим, что эта фигура уже ограничена двумя треугольными основаниями и тремя равнобедренными трапециями.
Предположим, что высота полученной фигуры равна h, длины сторон нижнего и верхнего оснований составляют a1 и a2 соответственно, а апотема (высота трапеции) равна ab. Тогда площадь поверхности усеченной пирамиды можно вычислить по формуле:
S = 3/2*(a1+a2)*ab + √3/4*(a12 + a22)
Здесь первое слагаемое – это площадь боковой поверхности, второе слагаемое – площадь треугольных оснований.
Объем фигуры рассчитывается следующим образом:
V = √3/12*h*(a12 + a22 + a1*a2)
Для однозначного определения характеристик усеченной пирамиды необходимо знать три ее параметра, что демонстрируют приведенные формулы.
Периметр и апофема правильной пирамиды
Свойства
Зная периметр основания правильной пирамиды, можно легко вычислить сторону основания, разделив периметр на удвоенное количество сторон многоугольника. Площадь основания в свою очередь будет рассчитываться по стандартной формуле площади правильного многоугольника, в которую необходимо будет подставить выражение, соответствующее стороне основания через периметр. a=P/n S=(na^2)/(4 tan〖(180°)/n〗 )=P^2/(4n tan〖(180°)/n〗 )
Чтобы найти радиус окружности, вписанной в правильный многоугольник в основании пирамиды, как и радиус окружности, описанной вокруг основания, необходимо знать сторону основания, поэтому здесь также пригодится полученное через периметр выражение. (рис.34.1,34.2) r=a/(2 tan〖(180°)/n〗 )=P/(2n tan〖(180°)/n〗 ) R=a/(2 sin〖(180°)/n〗 )=P/(2n sin〖(180°)/n〗 )
Величина внутреннего угла многоугольника в основании зависит только от количества сторон многоугольника и рассчитывается по следующей формуле. (рис.34.3) γ=180°(n-2)/n
Зная апофему и сторону основания правильной пирамиды, вычисленной через периметр, можно рассчитать боковое ребро и высоту пирамиды по теореме Пифагора в прямоугольных треугольниках. (рис. 34.4, 35.1) h=√(l^2-r^2 )=√(l^2-(P/(2n tan〖(180°)/n〗 ))^2 ) b=√(l^2+P^2/(4n^2 ))
Чтобы найти угол между основанием и апофемой, а также между основанием и боковым ребром, нужно сначала рассчитать косинусы этих углов в прямоугольных треугольниках, образованных высотой и соответствующим отрезком, которые через основание будут соединяться радиусы вписанной и описанной окружностей. (рис.34.4, 34.5) cosα=R/b=P/(2n sin〖(180°)/n〗 √(l^2+P^2/(4n^2 ))) cosβ=r/l=P/(2nl tan〖(180°)/n〗 )
Площадь боковой поверхности правильной пирамиды через периметр основания равна произведению периметра на половину апофемы. Площадь полной поверхности вычисляется как сумма полученного значения и площади основания. S_(б.п.)=lP/2 S_(п.п.)=P(l/2+P/(2n tan〖(180°)/n〗 ))
Чтобы найти объем пирамиды, необходимо знать не только периметр основания для расчета его площади, но и высоту пирамиды, которая равна квадратному корню из разности квадратов апофемы и радиуса вписанной в основание окружности. V=1/3 S_(осн.) h=(P^2 √(l^2-(P/(2n tan〖(180°)/n〗 ))^2 ))/(12n tan〖(180°)/n〗 )
Сфера, которую можно вписать в пирамиду, должна иметь радиус, равный отношению трех объемов к площади полной поверхности, которые можно вычислить через периметр и апофему пирамиды. Радиус сферы, которую можно описать вокруг пирамиды, должен быть равен квадрату боковой стороны, деленному на удвоенную высоту. (рис.34.6, 34.7) r_1=3V/S_(п.п.) =(P√(l^2-(P/(2n tan〖(180°)/n〗 ))^2 ))/(2n tan〖(180°)/n〗 (l/2+P/(2n tan〖(180°)/n〗 )) ) R_1=b^2/2h=(2l^2+P^2/n^2 )/(2√(l^2-(P/(2n tan〖(180°)/n〗 ))^2 ))
Геометрические фигуры. Правильная пирамида.
Правильная пирамида – когда основанием пирамиды является правильный многоугольник, а высота проецируется в центр основания (или проходит через него).
В правильной пирамиде все боковые ребра имеют одинаковую величину, и каждая боковая грань является равнобедренными треугольниками одного размера.
Правильная пирамида обладает следующими свойствами:
Формулы для правильной пирамиды.
V – объем пирамиды,
S – площадь основания пирамиды,
h – высота пирамиды,
Sb – площадь боковой поверхности пирамиды,
a – апофема (не путать с α) пирамиды,
P – периметр основания пирамиды,
n – число сторон основания пирамиды,
b – длина бокового ребра пирамиды,
α – плоский угол при вершине пирамиды.
Ниже указанная формула определения объема используется лишь для правильной пирамиды:
V – объем правильной пирамиды,
h – высота правильной пирамиды,
n – количество сторон правильного многоугольника, основания правильной пирамиды,
a – длина стороны правильного многоугольника.
Боковое ребро правильной пирамиды находят по формуле:
где b — боковое ребро правильной пирамиды (SA, SB, SC, SD либо SE),
n — количество сторон правильного многоугольника (основание правильной пирамиды),
a — сторона правильного многоугольника (AB, BC, CD, DE либо EA) – основания правильной пирамиды,
h — высота правильной пирамиды (OS).
Указания к решению задач. Свойства, которые мы перечислили выше, помогают при практическом решении. Когда нужно определить углы наклона граней, их поверхность и так далее, значит общая методика сводится к разбиению всей объемной фигуры на отдельные плоские фигуры и применение их свойств для определения отдельных элементов пирамиды, так как большинство элементов оказываются общими для нескольких фигур.
Нужно разбить всю объемную фигуру на отдельные элементы – треугольники, квадраты, отрезки. Дальше, к отдельным элементам применяем знания из курса планиметрии, что очень упрощает определение ответа.
Правильная треугольная пирамида.
Правильная треугольная пирамида – это пирамида, у которой основанием оказывается правильный треугольник, а вершина опускается в центр основания.
Формулы для правильной треугольной пирамиды.
Формула для нахождения объема правильной треугольной пирамиды:
V – объем правильной пирамиды, которая имеет в основании правильный (равносторонний) треугольник,
h – высота правильной пирамиды,
a – длина стороны основания правильной пирамиды.
Так как правильная треугольная пирамида – это частный случай правильной пирамиды, значит, формулы, верные для правильной пирамиды, оказываются верными и для правильной треугольной.
Еще одним частным случаем правильно пирамиды является тетраэдр.
[spoiler title=”источники:”]
http://geleot.ru/education/math/geometry/calc/pyramid/perimeter_and_apothem
http://www.calc.ru/Geometricheskiye-Figury-Pravilnaya-Piramida.html
[/spoiler]
Примечание. Если Вам необходимо решить задачу по геометрии, которой здесь нет – пишите об этом в форуме. В задачах вместо символа “квадратный корень” применяется функция sqrt(), в которой sqrt – символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак “√”.
Задача.
Боковая грань правильной треугольной пирамиды представляет собой правильный треугольник, площадь которого 16 корней из 3 см2 (16√3). Вычислить периметр основания пирамиды.
Решение.
Правильный треугольник – это равносторонний треугольник. Соответственно, боковая грань пирамиды представляет собой равносторонний треугольник.
Площадь равностороннего треугольника равна:
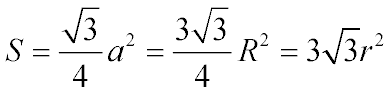
Соответственно:
16√3 = a2 √3 / 4
16 = a2 / 4
a2 = 64
a = 8 см
Основанием правильной треугольной пирамиды является правильный (равносторонний) треугольник. Таким образом, периметр основания пирамиды равен
8 * 3 = 24 см
Ответ: 24 см.
0
Правильная треугольная пирамида (правильная пирамида с треугольником в основании). Тетраэдр |
Описание курса
| Объем правильной треугольной пирамиды
