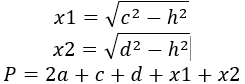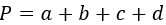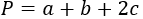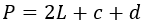Как найти периметр трапеции через диагонали - Сайт, где вы сможете решить свои вопросы

Как найти периметр трапеции

Содержание:

Основные свойства трапеции
Способы нахождений периметра
- По всем сторонам
- По сторонам равнобедренной трапеции
- Через среднюю линию
Примеры решения задач

Определения

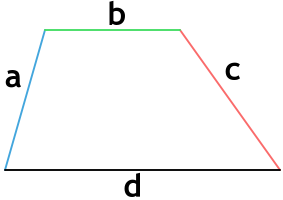
Трапеция — это четырехугольник, у которого лишь одна пара противолежащих сторон параллельна.

Периметр трапеции — это сумма длин всех его сторон.

Основные свойства трапеции

средняя линия трапеции параллельна ее основаниям, а также равна половине их суммы;

Свойство 1

биссектриса любого угла данного четырехугольника отсекает на его основании отрезок, равный боковой стороне;

Свойство 2

треугольники ABO и DCO (на картинке), образованные диагоналями фигуры и ее основаниями, подобны;

Свойство 3

треугольники OAB и OCD, образованные диагоналями трапеции и ее боковыми сторонами, имеют одинаковую площадь;

Свойство 4

если сумма длин оснований четырехугольника равна сумме его боковых ребер, то в фигуру можно вписать окружность;

Свойство 5

точки M и N середины диагоналей лежат на одной прямой со средней линией фигуры. Также отрезок MN равен полуразность оснований четырехугольника;

Свойство 6

середины оснований фигуры, точка пересечения ее диагоналей, а также точка пересечения продолжений ее боковых сторон лежат на одной прямой;

Свойство 7

Свойства равнобедренной трапеции

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

в равнобедренной трапеции углы при обоих ее основаниях одинаковы;
диагонали равны;
равнобедренную трапецию всегда можно вписать в окружность или описать окружность вокруг;
если диагонали перпендикулярны, то высота фигуры равна полусумме ее оснований.

Способы нахождений периметра

Рассмотрим способы, с помощью которых можно найти сумму длин всех сторон данного четырехугольника.

По всем сторонам

Периметр по всем сторон

Формула для нахождения периметра выглядит так:

P=a+b+c+d

где a, b, c, d — стороны трапеции.

По сторонам равнобедренной трапеции

Периметр по сторон 2

Если нам известны ребра этого четырехугольника с одинаковыми боковыми сторонами, то находить ее P можно по следующей формуле:

(P=2times a+b+c)

или

(P=2times c+a+b)

Через среднюю линию

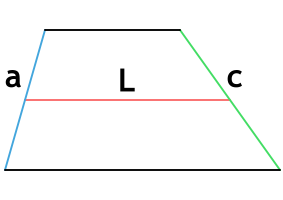
Так как средняя линия трапеции равна полусумме ее оснований, то формулу P можно выразить так:

(P=2times l+AB+CD)

где l — средняя линия фигуры.

Примеры решения задач

Давайте рассмотрим наглядные примеры решения задач на нахождение суммы длин всех ребер этой фигуры.

Задача 1

Дана трапеция с боковыми сторонами 4 см и 5 см, а ее основания равны 7 см и 10 см. Найти периметр данного многоугольника.

Решение:

Нам пригодится самая первая формула для расчета:

P=a+b+c+d.

Подставляем значения и получаем:

P=4+7+5+10=26;см.

Ответ: 26 см.

Задача 2

Известно, что у трапеции две боковые стороны равны 7 см, а ее основания равны 5 см и 8 см. Нужно найти P четырехугольника.

Решение:

Так как трапеция равнобедренная, удобнее всего будет использовать формулу:

(P=2times a+b+c)

Таким образом, получается:

(P=2times 7+5+8=27) см.

Ответ: 27 см.

Задача 3

Средняя линия l трапеции равна 6 см, а боковые стороны 5 см и 9 см. Вычислить P фигуры.

Решение:

Считать будем по формуле

(P=2times l+a+c)

(P=2times 6+5+9=26) см.

Ответ: 26 см.

Насколько полезной была для вас статья?

Рейтинг: 3.82 (Голосов: 11)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Текст с ошибкой:

Расскажите, что не так

Поиск по содержимому

Источник

Трапеция. Формулы, признаки и свойства трапеции

Определение.

Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

Параллельные стороны называются основами трапеции, а две другие боковыми сторонами

Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.

Элементы трапеции:

Основы трапеции – параллельные стороны
Боковые стороны – две другие стороны
Средняя линия – отрезок, соединяющий середины боковых сторон.

Виды трапеций:

Равнобедренная трапеция – трапеция, у которой боковые стороны равны
Прямоугольная трапеция – трапеция, у которой одна из боковых сторон перпендикулярна основам

Основные свойства трапеции

1. В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:

AB + CD = BC + AD

2. Средняя линия трапеции разделяет пополам любой отрезок, который соединяет основы, так же делит диагонали пополам:

AK = KB, AM = MC, BN = ND, CL = LD

3. Средняя линия трапеции параллельна основаниям и равна их полусумме:

4. Точка пересечения диагоналей трапеции и середины оснований лежат на одной прямой.

5. В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.

6. Каждая диагональ в точке пересечения делится на две части с таким соотношением длины, как соотношение между основаниями:

BC : AD = OC : AO = OB : DO

7. Диагонали трапеции d₁ и d₂ связаны со сторонами соотношением:

d₁² + d₂² = 2ab + c² + d²

Сторона трапеции

Формулы определения длин сторон трапеции:

1. Формула длины оснований трапеции через среднюю линию и другую основу:

a = 2m – b

b = 2m – a

2. Формулы длины основ через высоту и углы при нижнем основании:

a = b + h · (ctg α + ctg β)

b = a – h · (ctg α + ctg β)

3. Формулы длины основ через боковые стороны и углы при нижнем основании:

a = b + c·cos α + d·cos β

b = a – c·cos α – d·cos β

4. Формулы боковых сторон через высоту и углы при нижнем основании:

Средняя линия трапеции

Определение.

Средняя линия – отрезок, соединяющий середины боковых сторон трапеции.

Формулы определения длины средней линии трапеции:

1. Формула определения длины средней линии через длины оснований:

2. Формула определения длины средней линии через площадь и высоту:

Высота трапеции

Формулы определения длины высоты трапеции:

1. Формула высоты через сторону и прилегающий угол при основании:

h = c·sin α = d·sin β

2. Формула высоты через диагонали и углы между ними:

h =	sin γ ·	d₁ d₂	=	sin δ ·	d₁ d₂
a + b	a + b

3. Формула высоты через диагонали, углы между ними и среднюю линию:

h =	sin γ ·	d₁ d₂	=	sin δ ·	d₁ d₂
2m	2m

4. Формула высоты трапеции через площадь и длины оснований:

5. Формула высоты трапеции через площадь и длину средней линии:

Диагонали трапеции

Формулы определения длины диагоналей трапеции:

1. Формулы диагоналей по теореме косинусов:

d₁ = √a² + d² – 2ad·cos β

d₂ = √a² + c² – 2ac·cos α

2. Формулы диагоналей через четыре стороны:

d₁ =	√	d ² + ab –	a(d ² – c²)
a – b

d₂ =	√	c² + ab –	a(c² – d ²)
a – b

3. Формула длины диагоналей через высоту:

d₁ = √h² + (a – h · ctg β)² = √h² + (b + h · ctg α)²

d₂ = √h² + (a – h · ctg α)² = √h² + (b + h · ctg β)²

4. Формулы длины диагонали через сумму квадратов диагоналей:

d₁ = √c² + d ² + 2ab – d₂²

d₂ = √c² + d ² + 2ab – d₁²

Площадь трапеции

Формулы определения площади трапеции:

1. Формула площади через основания и высоту:

2. Формула площади через среднюю линию и высоту:

S = m · h

3. Формула площади через диагонали и угол между ними:

S =	d₁d₂	· sin γ	=	d₁d₂	· sin δ
2	2

4. Формула площади через четыре стороны:

S =	a + b	√	c² –	(	(a – b)² + c² – d ²	)	²
2	2(a – b)

5. Формула Герона для трапеции

S =	a + b	√(p – a)(p – b)(p – a – c)(p – a – d)
\|a – b\|

где

p =	a + b + c + d	– полупериметр трапеции.
2

Периметр трапеции

Формула определения периметра трапеции:

1. Формула периметра через основания:

P = a + b + c + d

Окружность описанная вокруг трапеции

Окружность можно описать только вокруг равнобедренной трапеции!!!

Формула определения радиуса описанной вокруг трапеции окружности:

1. Формула радиуса через стороны и диагональ:

R =	a·c·d₁
4√p(p – a)(p – c)(p – d₁)

где

a – большее основание

Окружность вписанная в трапецию

В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:

a + b = c + d

Формула определения радиуса вписанной в трапецию окружности

1. Формула радиуса вписанной окружности через высоту:

Другие отрезки разносторонней трапеции

Формулы определения длин отрезков проходящих через трапецию:

1. Формула определения длин отрезков проходящих через трапецию:

KM = NL =	b	KN = ML =	a	TO = OQ =	a · b
2	2	a + b

Источник

Рассчитать периметр трапеции с помощью калькулятора или самостоятельно по формуле поможет материалы этой страницы. Кроме того вы можете рассчитать периметр равнобедренной трапеции.

Содержание:

калькулятор периметра трапеции
формула периметра трапеции через 4 стороны
формула периметра трапеции через среднюю линию и боковые стороны
примеры задач

Трапеция – выпуклый четырехугольник у которого две стороны параллельны (их называют основаниями), а две другие стороны, которые называют боковые стороны, непараллельны.

Периметр других четырехугольников также можно рассчитать на сайте: квадрат, прямоугольник, параллелограмм, ромб.

Формула периметра трапеции через все стороны

{P = a+b+c+d}

a, b, c и d – стороны трапеции

Формула периметра трапеции через среднюю линию и боковые стороны

{P = a+c+2L}

a и c – боковые стороны трапеции

L – средняя линия трапеции

Пример задачи на нахождение периметра трапеции

Задача 1

Найдите периметр трапеции если ее основания равны 7см и 10см а боковые стороны 4см и 5см.

Решение

Применим первую формулу. Подставим в нее значения длин сторон трапеции и рассчитаем ее периметр:

P = a+b+c+d = 4+7+5+10 = 26 : см

Ответ: 26 см

Осталось проверить ответ с помощью калькулятора .

Источник

Периметр трапеции калькулятор онлайн умеет вычислять периметр четырьмя способами:

По четырем сторонам.
По основанию и боковой стороне равнобедренной трапеции.
По средней линии и боковым сторонам.
По высоте и верхнему основанию и боковым сторонам.

Сделав расчет периметра на этом онлайн калькуляторе Вы получите не только ответ, но и детальное, пошаговое решение с выводом формул и промежуточных действий.

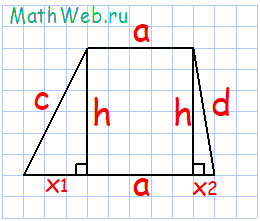
Трапеция – это четырехугольник, у которого две стороны параллельны (основания), а две другие не параллельны (боковые стороны).
Формула периметра трапеции:
где a – верхнее основание, h – высота, с и d – боковые стороны.

Решение:

x1 = √c² – h²

= √4² – 3²

= √16 – 9

= 2.646

x2 = √d² – h²

= √4² – 3²

= √16 – 9

= 2.646

P = 2a + c + d + x1 + x2

= 2·8 + 4 + 4 + 2.646 + 2.646

29.292

Ответ: Периметр трапеции с верхним основанием a = 8 высотой h = 3 и боковыми сторонами с = 4, d = 4 равен 29.292

Периметр трапеции – это сумма четырех сторон.
Так как, довольно часто, не все стороны известны, то периметр может быть найден и по другим формулам. Вывод этих формул основан на правилах геометрии и тригонометрии.

Как найти периметр трапеции?

Найти периметр трапеции очень просто на нашем онлайн калькуляторе. Так же периметр может быть найден самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.

1) По четырем сторонам

где a,b,c,d – стороны трапеции.

2) По основанию и боковой стороне равнобедренной трапеции

где a,b,c – стороны трапеции.

3) По средней линии и боковым сторонам

где c,d – боковые стороны и L – длина средней линии.

4) По высоте и верхнему основанию и боковым сторонам

ггде a – верхнее основание, h – высота, с и d – боковые стороны.

Скачать все формулы в формате Word

Источник

Download Article

A trapezoid is defined as a quadrilateral with two parallel sides. As with any polygon, to find the perimeter of a trapezoid you need to add all four of its sides together. However, often you will be missing side lengths but have other information, such as the height of the trapezoid, or the angle measurements. Using this information, you can use rules of geometry and trigonometry to find the unknown lengths of sides.

1

Set up the formula for perimeter of a trapezoid. The formula is , where equals the perimeter of the trapezoid, and the variables equals the length of the top base of the trapezoid, equals the length of the bottom base, equals the length of the left side, and equals the length of the right side.^[1]
2
Plug the side lengths into the formula. If you do not know the length of all four sides of the trapezoid, you cannot use this formula.
- For example, if you have a trapezoid with a top base of 2 cm, a bottom base of 3 cm, and two side lengths of 1 cm, your formula will look like this:
Advertisement
3

Add the side lengths together. This will give you the perimeter of your trapezoid.

1
Divide the trapezoid into a rectangle and two right triangles. To do this, draw the height from both top vertices.
- If you cannot form two right triangles because one side of the trapezoid is perpendicular to the base, just note that this side will have the same measurement as the height, and divide the trapezoid into one rectangle and one right triangle.
2
Label each height line. Since these are opposite sides of a rectangle, they will be the same length.^[2]
- For example, if you have a trapezoid with a height of 6 cm, you should draw a line from each top vertex extending down to the bottom base. Label each line 6 cm.
3
Label the length of the middle section of the bottom base. (This is the bottom side of the rectangle.) The length will equal the length of the top base (the top side of the rectangle), because opposite sides of a rectangle are of equal length.^[3] If you do not know the length of the top base, you cannot use this method.
- For example, if the top base of the trapezoid is 6 cm, then the middle section of the bottom base is also 6 cm.
4

Set up the Pythagorean Theorem formula for the first right triangle. The formula is $a^{{2}}+b^{{2}}=c^{{2}}$ , where is the length of the hypotenuse of the right triangle (the side opposite the right angle), is the height of the right triangle, and is the length of the base of the triangle.^[4]
5
6

Square the known values in the equation. Then, subtract to isolate the variable.
7

Take the square root to find the value of . (For complete instructions on how to simplify square roots, you can read Simplify a Square Root.) The result will give you the value of the missing base of your first right triangle. Label this length on the base of your triangle.
8

Find the missing length of the second right triangle. To do this, set up the Pythagorean Theorem formula for the second triangle, and follow the steps to find the length of the missing side. If you are working with an isosceles trapezoid, which is a trapezoid in which the two non-parallel sides are the same length,^[5] the two right triangles are congruent, so you can simply carry the value from the first triangle over to the second triangle.
9

Add up all the side lengths of the trapezoid. The perimeter of any polygon is the sum of all sides: . For the bottom base, you will add the bottom side of the rectangle, plus the bases of the two triangles. You will likely have square roots in your answer. For complete instructions on how to add square roots, you can read the article Add Square Roots. You can also use a calculator to convert the square roots to decimals.

1
Divide the trapezoid into a rectangle and two right triangles. To do this, draw the height from both top vertices.
- If you cannot form two right triangles because one side of the trapezoid is perpendicular to the base, just note that this side will have the same measurement as the height, and divide the trapezoid into one rectangle and one right triangle.
2
Label each height line. Since these are opposite sides of a rectangle, they will be the same length.^[6]
- For example, if you have a trapezoid with a height of 6 cm, you should draw a line from each top vertex extending down to the bottom base. Label each line 6 cm.
3
Label the length of the middle section of the bottom base. (This is the bottom side of the rectangle.) This length will be equal to the length of the top base, because opposite sides of a rectangle are of equal length.^[7]
- For example, if the top base of the trapezoid is 6 cm, then the middle section of the bottom base is also 6 cm.
4
5
Plug the known values into the sine ratio. Make sure you use the height of the triangle as the length of the opposite side in the formula. You will solve for H.
- For example, if the given interior angle is 35 degrees, and the height of the triangle is 6 cm, your formula will look like this:
  $sin(35)={frac {6}{H}}$
6
Find the sine of the angle. Do this by using the SIN button on a scientific calculator. Plug this value into the ratio.
- For example, by using a calculator you will find that the sine of a 35 degree angle is .5738 (rounded). So your formula will now be:
  $.5738={frac {6}{H}}$
7

Solve for H. To do this, multiply each side by H, then divide each side by the angle sine. Or, you can simply divide the height of the triangle by the angle sine.
8

Find the length of the hypotenuse of the second right triangle. Set up the sine ratio ( $sin theta ={frac {{text{opposite}}}{{text{hypotenuse}}}}$ ) for the second given interior angle. This will give you the length of the hypotenuse, which is also the first side of the trapezoid.
9

Set up the Pythagorean Theorem formula for the first right triangle. The Pythagorean Theorem formula is $a^{{2}}+b^{{2}}=c^{{2}}$ , where the length of the hypotenuse is , and the height of the triangle is .
10
11

Solve for . This will give you the length of base of the first right triangle, and the first missing section of the trapezoid’s bottom base.
12
13
Add up all the side lengths of the trapezoid. The perimeter of any polygon is the sum of all sides: . For the bottom base, you will add the bottom side of the rectangle, plus the bases of the two triangles.
- For example,
  So, the approximate perimeter of your trapezoid is 45.5059 cm.

Add New Question

Question

How can I solve the hypotenuse of a right triangle with a height of 2ft?

You don’t have enough information to find the hypotenuse. You would need the lengths of both legs or the size of at least one of the acute angles or the area of the triangle.
Question

How do I find the area without knowing the length of the sides of the trapezoid?

You would have to know the height of the trapezoid (h) and the lengths of both parallel sides (a and b). The area formula is [h(a + b)] / 2.
Question

Why are there so many formulas?

It’s because there are several possible sets of known dimensions regarding a trapezoid.

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Use the laws of special triangles to find the missing lengths of special triangles without using sine or the Pythagorean Theorem. The laws apply to a 30-60-90 triangle, or a 90-45-45 triangle.
Use a scientific calculator to find the sine of an angle by entering the angle measurement, then hitting the “SIN” button. You can also use a trigonometry table.

Thanks for submitting a tip for review!

Things You’ll Need

Calculator
Pencil
Paper

References

About This Article

Article SummaryX

To find the perimeter of a trapezoid if you know the length of both sides and the bases, add together the length of all 4 sides. If you know the height, both side lengths, and the top base length, draw a straight line down from each top corner to form a square and 2 triangles. Then, use the Pythagorean Theorem to find the length of the base of each triangle. Add the length of each triangle base to the length of the top base, then add that to the top base and both sides to get the perimeter. To learn more about using the Pythagorean Theorem, keep reading!

Did this summary help you?

Thanks to all authors for creating a page that has been read 264,180 times.

Did this article help you?

Источник

Как найти периметр трапеции

Основные свойства трапеции

Способы нахождений периметра

По всем сторонам

По сторонам равнобедренной трапеции

Через среднюю линию

Примеры решения задач

Текст с ошибкой:

Поиск по содержимому

Трапеция. Формулы, признаки и свойства трапеции

Основные свойства трапеции

Сторона трапеции

Формулы определения длин сторон трапеции:

Средняя линия трапеции

Формулы определения длины средней линии трапеции:

Высота трапеции

Формулы определения длины высоты трапеции:

Диагонали трапеции

Формулы определения длины диагоналей трапеции:

Площадь трапеции

Формулы определения площади трапеции:

Периметр трапеции

Формула определения периметра трапеции:

Окружность описанная вокруг трапеции

Формула определения радиуса описанной вокруг трапеции окружности:

Окружность вписанная в трапецию

Формула определения радиуса вписанной в трапецию окружности

Другие отрезки разносторонней трапеции

Формулы определения длин отрезков проходящих через трапецию:

Содержание:

Формула периметра трапеции через все стороны

Формула периметра трапеции через среднюю линию и боковые стороны

Пример задачи на нахождение периметра трапеции

Как найти периметр трапеции?

1) По четырем сторонам

2) По основанию и боковой стороне равнобедренной трапеции

3) По средней линии и боковым сторонам

4) По высоте и верхнему основанию и боковым сторонам

Things You’ll Need

References

About This Article

Did this article help you?

Вам также может понравиться

Как составить патент в налоговую

Закон менделеева клапейрона формула как найти объем

Как найти вероятность что дверь будет открыта

Добавить комментарий Отменить ответ