Как найти периметр треугольника

О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение
Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской буквой P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах и ходе решении.
Важно, чтобы все параметры были переданы в одной единице длины, иначе мы не сможем подсчитать результат. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
В чем измеряется периметр:
Как узнать периметр треугольника
Рассмотрим какие существуют формулы, и при каких известных исходных данных их можно применять.
Если известны три стороны, то периметр треугольника равен их сумме. Этот способ проходят во втором классе.
P = a + b + c, где a, b, c — длина стороны.
Если известна площадь и радиус вписанной окружности:
P = 2 * S : r, где S — площадь, r — радиус вписанной окружности.
Если известны две стороны и угол между ними, вычислить периметр треугольника можно так:
P = √ b 2 + с 2 – 2 * b * с * cosα + (b + с), где b, с — известные стороны, α — угол между известными сторонами.
Если известна одна сторона в равностороннем треугольнике:
P = 3 * a, где a — длина стороны.
Все стороны в равносторонней фигуре равны.
Если известна боковая сторона и основание в равнобедренном треугольнике:
P = 2 * a + b, где a — боковая сторона, b — основание.
Боковые стороны в равнобедренной фигуре равны.
Если известна боковая сторона и высота в равнобедренном треугольнике:
P = 2 * (√ a 2 + h 2 ) + 2 * a, где a — боковая сторона, h — высота.
Высотой принято называть отрезок, который вышел из вершины и опустился на основание. В равнобедренной фигуре высота делит основание пополам.
Если известны катеты в прямоугольном треугольнике:
P = √ a 2 + b 2 + (a + b), где a, b — катеты.
Катет — одна из двух сторон, которые образуют прямой угол.
Если известны катет и гипотенуза в прямоугольном треугольнике:
P = √ c 2 – a 2 + (a + c), где a — любой катет, c — гипотенуза.
Гипотенуза — сторона, которая лежит напротив прямого угла.
Скачать онлайн таблицу
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
Периметр прямоугольника

Периметр прямоугольника — это сумма
всех сторон прямоугольника.
Периметр прямоугольника можно рассчитать
через четыре стороны, через смежные стороны,
через диагональ, через площадь,
через радиус описанной окружности.
Самый простой способ найти периметр
прямоугольника, это сложить все стороны.
Также, исходя из свойства прямоугольника, — «противоположные
стороны равны и параллельны», можно сказать, что периметр
численно равен удвоенной сумме ширины и высоты — двух
смежных сторон прямоугольника.
Кроме этих двух способов периметр прямоугольника
можно найти через другие величины. Например, через
площадь прямоугольника, диагональ прямоугольника, и так далее.
В прямоугольник невозможно вписать окружность,
поэтому выразить периметр через вписанную
окружность не получится.
Единицы измерения периметра прямоугольника:
км, м, дм, см, мм.
Формулы периметра прямоугольника
- Периметр прямоугольника через четыре стороны
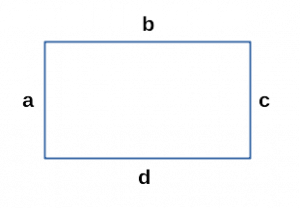
a, b, c, d — стороны прямоугольника;
a || c, b || d;
a = c, b = d;
Периметр прямоугольника через смежные стороны 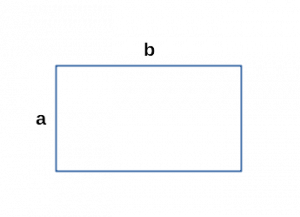
a, b — смежные стороны;
a ≠ b;
Периметр прямоугольника через любую сторону и диагональ 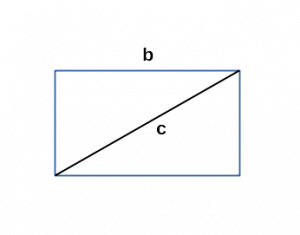
b — любая сторона;
c — диагональ;
Периметр прямоугольника через любую сторону и площадь 
b — любая сторона;
S — площадь;
Периметр прямоугольника через любую сторону и радиус описанной окружности 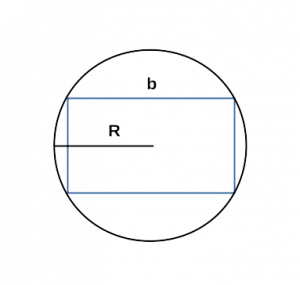
b — любая сторона;
R — радиус описанной окружности;
Полупериметр
Полупериметр — это половина периметра.
Обозначается латинской буквой p.
Чтобы найти полупериметр нужно разделить
периметр на два, или домножить периметр на 0.5.
[ p = frac
<2>= P cdot 0.5 ]
Полупериметр применяется в некоторых формулах
нахождения разных величин прямоугольника. Вместо того,
чтобы вычислять периметр, в таких формулах
удобней вычислять полупериметр.
Основные определения и величины
Длина прямоугольника — это длинная сторона
/ наибольшая сторона прямоугольника.
Обозначается латинской буквой a.
Ширина прямоугольника — это широкая сторона
/ наименьшая сторона прямоугольника.
Обозначается латинской буквой b.
Сторона прямоугольника — это ширина или длина прямоугольника,
в зависимости от численного значения длины стороны.
Обозначается латинской буквой a или b.
Диагональ прямоугольника — это отрезок, соединяющий
противоположные стороны прямоугольника.
Обозначается латинской буквой c или d.
Средняя линия прямоугольника — это отрезок, соединяющий
наименьшие параллельные стороны прямоугольника друг с
другом, причем делящий их пополам на равные отрезки.
Обозначается латинской буквой l.
Радиус описанной окружности прямоугольника — это отрезок,
соединяющий центр описанной около треугольника
окружности и произвольную точку на окружности.
Обозначается латинской буквой R.
Высота прямоугольника — это любая сторона прямоугольника,
а также любой отрезок в прямоугольнике, образующий угол в 90 градусов.
Обозначается латинской буквой h.
Периметр и диагональ прямоугольника

Свойства
Зная периметр прямоугольника и его диагональ можно составить систему уравнений с двумя неизвестными, благодаря которой становится возможным решить задачу методом подстановки. (Рис.56.1) <█(P=2(a+b)@a^2+b^2=d^2 )┤
Чтобы решить такую систему, необходимо выразить одну сторону из первого уравнения. P=2(a+b) P=2a+2b 2a=P-2b a=P/2-b
Теперь полученное выражение для переменной «a» подставляем во второе уравнение и находим значение переменной «b». (P/2-b)^2+b^2=d^2 〖P^2/4-Pb+b^2+b〗^2=d^2 〖2b〗^2-Pb+P^2/4-d^2=0
Получилось квадратное уравнение, для решения которого нужно найти дискриминант. D=b^2-4ac=P^2-4*2*(P^2/4-d^2 )=P^2-2P^2+8d^2=8d^2-P^2
В данном уравнении при значении дискриминанта больше либо равном нулю 8d^2-P^2 ≥ 0, будет два решения. Это и будут обе стороны прямоугольника x=(-b±√(b^2-4ac))/2a b=(P+√(8d^2-P^2 ))/4 a=(P-√(8d^2-P^2 ))/4
Углы пересечения диагоналей со сторонами α и β можно найти из соотношения сторон в прямоугольном треугольнике, образованном диагональю. Тангенс угла α равен отношению b к a, а тангенс угла β равен отношению a к b. α=arc tan〖b/a〗 β=arc tan〖a/b〗
Вертикальные углы при пересечении диагоналей можно вычислить, удвоив величины углов α и β, как видно из рисунка. (рис. 56.2) γ=2α δ=2β
Радиус описанной окружности прямоугольника через диагональ вычисляется делением ее на два, так как точка пересечения диагоналей, которая является центром окружности, делит диагонали на две равные части – радиусы (рис. 56.3) R=d/2
[spoiler title=”источники:”]
http://colibrus.ru/perimetr-pryamougolnika/
http://geleot.ru/education/math/geometry/calc/rectangle/perimeter_and_diagonal
[/spoiler]
Выбирайте формулу в зависимости от известных величин.
1. Как найти периметр треугольника, зная три стороны
Просто посчитайте сумму всех сторон.
- P — искомый периметр;
- a, b, c — стороны треугольника.
2. Как найти периметр треугольника, зная его площадь и радиус вписанной окружности
Умножьте площадь треугольника на 2.
Разделите результат на радиус вписанной окружности.
- P — искомый периметр;
- S — площадь треугольника;
- r — радиус вписанной окружности.
3. Как вычислить периметр треугольника, зная две стороны и угол между ними
Сначала найдите неизвестную сторону треугольника с помощью теоремы косинусов:
- Умножьте одну сторону на вторую, на косинус угла между ними и на 2.
- Посчитайте сумму квадратов известных сторон и отнимите от неё число, полученное в предыдущем действии.
- Найдите корень из результата.
Теперь прибавьте к найденной стороне две ранее известные стороны.
- P — искомый периметр;
- b, c — известные стороны треугольника;
- ɑ — угол между известными сторонами;
- a — неизвестная сторона треугольника.
4. Как найти периметр равностороннего треугольника, зная одну сторону
Умножьте сторону на 3.
- P — искомый периметр;
- a — любая сторона треугольника (напомним, в равностороннем треугольнике все стороны равны).
5. Как вычислить периметр равнобедренного треугольника, зная боковую сторону и основание
Умножьте боковую сторону на 2.
Прибавьте к результату основание.
- P — искомый периметр;
- a — боковая сторона треугольника (в равнобедренном треугольнике боковые стороны равны);
- b — основание треугольника (это сторона, которая отличается длиной от остальных).
6. Как найти периметр равнобедренного треугольника, зная боковую сторону и высоту
Найдите квадраты боковой стороны и высоты.
Отнимите от первого числа второе.
Найдите корень из результата и умножьте его на 2.
Прибавьте к полученному числу две боковые стороны.
- P — искомый периметр;
- a — боковая сторона треугольника;
- h — высота (перпендикуляр, опущенный на основание треугольника со стороны противоположной вершины; в равнобедренном треугольнике высота делит основание пополам).
7. Как вычислить периметр прямоугольного треугольника, зная катеты
Найдите квадраты катетов и посчитайте их сумму.
Извлеките корень из полученного числа.
Прибавьте к результату оба катета.
- P — искомый периметр;
- a, b — катеты треугольника (стороны, которые образуют прямой угол).
8. Как найти периметр прямоугольного треугольника, зная катет и гипотенузу
Посчитайте квадраты гипотенузы и катета.
Отнимите от первого числа второе.
Найдите корень из результата.
Прибавьте катет и гипотенузу.
- P — искомый периметр;
- a — любой катет прямоугольника;
- c — гипотенуза (сторона, которая лежит напротив прямого угла).
Формулы периметра фигур
Периметр геометрической фигуры — длина границы геометрической фигуры.
- периметр треугольника
- периметр квадрата
- периметр прямоугольника
- периметр параллелограмма
- периметр ромба
- периметр трапеции
- длина окружности
Периметр треугольника
Периметр треугольника равен сумме длин его сторон.
P =a + b + c
,
где P — периметр треугольника,
a, b, c — длины сторон треугольника.
Периметр квадрата
Периметр квадрата по длине стороны
Периметр квадрата равен произведению длины его стороны на четыре.
P = 4 · a
,
где P — периметр квадрата,
a — длина стороны квадрата.
Периметр квадрата по длине диагонали
Периметр квадрата равен произведению длины его диагонали на два корня из двух.
P = 2 · 2 · d
,
где P — периметр квадрата,
d — длина диагонали квадрата.
Периметр прямоугольника
Периметр прямоугольника равен удвоенной сумме сторон, прилежащих к одному углу.
P = 2 · a + b
,
где P — периметр прямоугольника,
a, b — длины сторон прямоугольника.
Периметр параллелограмма
Периметр параллелограмма равен удвоенной сумме сторон, прилежащих к одному углу.
P = 2 · a + b
,
где P — периметр параллелограмма,
a, b — длина сторон параллелограмма.
Периметр ромба
Периметр ромба равен произведению длины его стороны на четыре.
P = 4 · a
,
где P — периметр ромба,
a — длина сторон ромба.
Периметр трапеции
Периметр трапеции равен сумме длин ее сторон.
P = a + b + c + d
,
где P — периметр трапеции,
a, b — длины основ трапеции,
c, d — длины боковых сторон трапеции.
Длина окружности
Длина окружности через радиус
Длина окружности равна удвоенному произведению радиуса на число пи.
P = 2 · π · r
,
где P — длина окружности,
r — радиус окружности.
Длина окружности через диаметр
Длина окружности равна произведению диаметра окружности на число пи.
P = π · d
,
где P — длина окружности,
d — диаметр окружности.
- Коротко о важном
- Таблицы
- Формулы
- Формулы по геометрии
- Теория по математике
Содержание:
- Формула периметра круга (длины окружности):
- Формула периметра треугольника:
- Формула периметра прямоугольника:
- Формулы периметра квадрата:
- Формула периметра трапеции:
- Формула периметра параллелограмма:
- Формула периметра ромба:
Периметр геометрической фигуры – суммарная длина границ плоской геометрической фигуры.
Периметр имеет ту же размерность величин, что и длина.
Формула периметра круга (длины окружности):
1) Периметр круга равен произведению радиуса на два пи (3.1415).
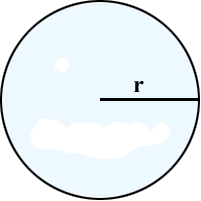
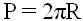
P – Периметр круга (длина окружности)
π – число пи (3.1415)
r – радиус круга (окружности)
См. также: Программа для расчета периметра круга (длины окружности).
Формула периметра треугольника:
1) Периметр треугольника равен сумме 3-ех его сторон (a, b, c).
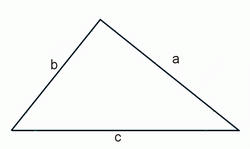
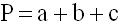
P – периметр треугольника
a, b, c – длины сторон треугольника
См. также: Программа для расчета периметра треугольника.
Формула периметра прямоугольника:
1) Периметр прямоугольника равен удвоенной сумме 2-х его смежных сторон (a, b).
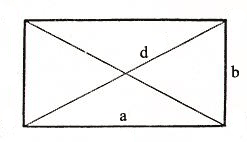
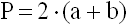
P – периметр прямоугольника
a – длина 1-ой стороны прямоугольника
b – длина 2-ой стороны прямоугольника
См. также: Программа для расчета периметра прямоугольника.
Формулы периметра квадрата:
1) Периметр квадрата равен сумме 4-х длин его сторон или произведению длины любой его стороны на четыре (так как у квадрат длины всех сторон равны).
2) Периметр квадрата равен произведению длины его диагонали на два корня из двух.
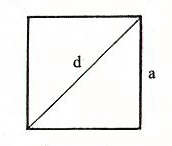
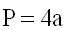
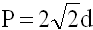
P – периметр квадрата
a – длина стороны квадрата
d – длина диагонали квадрата
См. также: Программа для расчета периметра квадрата.
Формула периметра трапеции:
1) Периметр трапеции равен сумме 4-х её сторон (a, b, c, d).
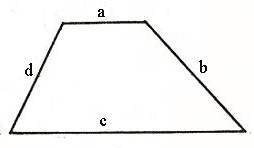
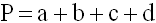
P – периметр трапеции
a, c – длины оснований трапеции
b, d – длины боковых сторон трапеции
См. также: Программа для расчета периметра трапеции.
Формула периметра параллелограмма:
1) Периметр параллелограмма равен удвоенной сумме 2-х его смежных сторон (a, b).
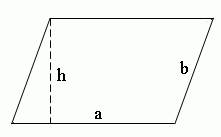
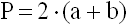
P – периметр параллелограмма
a – длина 1-ой стороны параллелограмма
b – длина 2-ой стороны параллелограмма
См. также: Программа для расчета периметра параллелограмма.
Формула периметра ромба:
1) Периметр ромба равен сумме 4-х длин его сторон или произведению
длины любой его стороны на четыре (так как у ромба длины всех сторон равны).
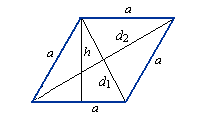
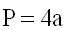
P – периметр ромба
a – длина стороны ромба
См. также: Программа для расчета периметра ромба.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Периметр треугольника калькулятор онлайн умеет вычислять периметр восемью способами:
- По трем сторонам.
- По площади и радиусу вписанной окружности.
- По двум сторонам и углу между ними.
- По стороне равностороннего треугольника.
- По боковой стороне и основанию равнобедренного треугольника.
- По боковой стороне и высоте равнобедренного треугольника.
- По катетам прямоугольного треугольника.
- По одному катету и гипотенузе прямоугольного треугольника.
Сделав расчет периметра на этом онлайн калькуляторе Вы получите не только ответ, но и детальное, пошаговое решение с выводом формул и промежуточных действий.
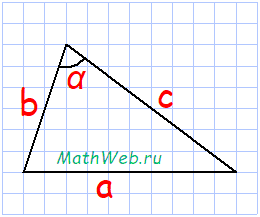
Треугольник – это геометрическая фигура, состоящая из трех точек (вершины треугольника), не лежащих на одной прямой, соедененных тремя отрезками (стороны треугольника).
Формула периметра треугольника: 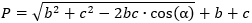
где b,c – стороны треугольника, α° – угол между ними.
Решение:
P = √b2 + с2 – 2bc·cos(α°) + b + c
= √12 + 12 – 2·1·1·cos(90°) + 1 + 1
= √1 + 1 – 0 + 2
= √2 + 2
= 1.414 + 2
=
3.414
Ответ: Периметр треугольника со сторонами b = 1, c = 1 и углом между ними α° = 90 равен 3.414
Периметр треугольника- это сумма трех сторон.
Периметр может быть найден и по другим формулам, вывод которых основан на поиске длины неизвестной стороны.
Как найти периметр треугольника?
Найти периметр треугольника очень просто на нашем онлайн калькуляторе. Так же периметр может быть найден самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.
1) По трем сторонам
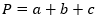
где a,b,c – стороны треугольника.
2) По площади и радиусу вписанной окружности
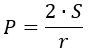
где S – площадь треугольника, r – радиус вписанной окружности.
3) По двум сторонам и углу между ними
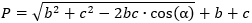
где b,c – стороны треугольника, α° – угол между ними.
4) По стороне равностороннего треугольника
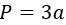
где a – сторона равностороннего треугольника.
5) По боковой стороне и основанию равнобедренного треугольника
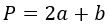
где a – боковая сторона и b – основание равнобедренного треугольника.
6) По боковой стороне и высоте равнобедренного треугольника
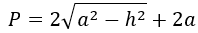
где a – боковая сторона и h – высота равнобедренного треугольника.
7) По катетам прямоугольного треугольника
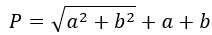
где a,b – катеты прямоугольного треугольника.
8) По одному катету и гипотенузе прямоугольного треугольника.
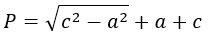
где а – катет и с – гипотенуза прямоугольного треугольника.
Скачать все формулы в формате Word











