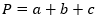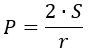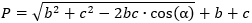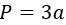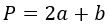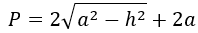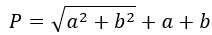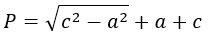Выбирайте формулу в зависимости от известных величин.
1. Как найти периметр треугольника, зная три стороны
Просто посчитайте сумму всех сторон.
- P — искомый периметр;
- a, b, c — стороны треугольника.
2. Как найти периметр треугольника, зная его площадь и радиус вписанной окружности
Умножьте площадь треугольника на 2.
Разделите результат на радиус вписанной окружности.
- P — искомый периметр;
- S — площадь треугольника;
- r — радиус вписанной окружности.
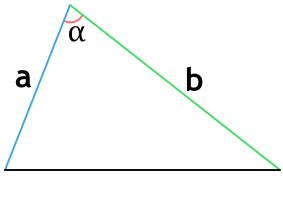
3. Как вычислить периметр треугольника, зная две стороны и угол между ними
Сначала найдите неизвестную сторону треугольника с помощью теоремы косинусов:
- Умножьте одну сторону на вторую, на косинус угла между ними и на 2.
- Посчитайте сумму квадратов известных сторон и отнимите от неё число, полученное в предыдущем действии.
- Найдите корень из результата.
Теперь прибавьте к найденной стороне две ранее известные стороны.
- P — искомый периметр;
- b, c — известные стороны треугольника;
- ɑ — угол между известными сторонами;
- a — неизвестная сторона треугольника.
4. Как найти периметр равностороннего треугольника, зная одну сторону
Умножьте сторону на 3.
- P — искомый периметр;
- a — любая сторона треугольника (напомним, в равностороннем треугольнике все стороны равны).
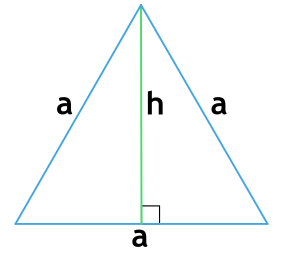
5. Как вычислить периметр равнобедренного треугольника, зная боковую сторону и основание
Умножьте боковую сторону на 2.
Прибавьте к результату основание.
- P — искомый периметр;
- a — боковая сторона треугольника (в равнобедренном треугольнике боковые стороны равны);
- b — основание треугольника (это сторона, которая отличается длиной от остальных).
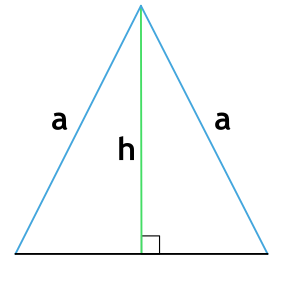
6. Как найти периметр равнобедренного треугольника, зная боковую сторону и высоту
Найдите квадраты боковой стороны и высоты.
Отнимите от первого числа второе.
Найдите корень из результата и умножьте его на 2.
Прибавьте к полученному числу две боковые стороны.
- P — искомый периметр;
- a — боковая сторона треугольника;
- h — высота (перпендикуляр, опущенный на основание треугольника со стороны противоположной вершины; в равнобедренном треугольнике высота делит основание пополам).
7. Как вычислить периметр прямоугольного треугольника, зная катеты
Найдите квадраты катетов и посчитайте их сумму.
Извлеките корень из полученного числа.
Прибавьте к результату оба катета.
- P — искомый периметр;
- a, b — катеты треугольника (стороны, которые образуют прямой угол).
8. Как найти периметр прямоугольного треугольника, зная катет и гипотенузу
Посчитайте квадраты гипотенузы и катета.
Отнимите от первого числа второе.
Найдите корень из результата.
Прибавьте катет и гипотенузу.
- P — искомый периметр;
- a — любой катет прямоугольника;
- c — гипотенуза (сторона, которая лежит напротив прямого угла).
Периметр треугольника калькулятор онлайн умеет вычислять периметр восемью способами:
- По трем сторонам.
- По площади и радиусу вписанной окружности.
- По двум сторонам и углу между ними.
- По стороне равностороннего треугольника.
- По боковой стороне и основанию равнобедренного треугольника.
- По боковой стороне и высоте равнобедренного треугольника.
- По катетам прямоугольного треугольника.
- По одному катету и гипотенузе прямоугольного треугольника.
Сделав расчет периметра на этом онлайн калькуляторе Вы получите не только ответ, но и детальное, пошаговое решение с выводом формул и промежуточных действий.
Периметр треугольника- это сумма трех сторон.
Периметр может быть найден и по другим формулам, вывод которых основан на поиске длины неизвестной стороны.
Как найти периметр треугольника?
Найти периметр треугольника очень просто на нашем онлайн калькуляторе. Так же периметр может быть найден самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.
1) По трем сторонам
где a,b,c – стороны треугольника.
2) По площади и радиусу вписанной окружности
где S – площадь треугольника, r – радиус вписанной окружности.
3) По двум сторонам и углу между ними
где b,c – стороны треугольника, α° – угол между ними.
4) По стороне равностороннего треугольника
где a – сторона равностороннего треугольника.
5) По боковой стороне и основанию равнобедренного треугольника
где a – боковая сторона и b – основание равнобедренного треугольника.
6) По боковой стороне и высоте равнобедренного треугольника
где a – боковая сторона и h – высота равнобедренного треугольника.
7) По катетам прямоугольного треугольника
где a,b – катеты прямоугольного треугольника.
8) По одному катету и гипотенузе прямоугольного треугольника.
где а – катет и с – гипотенуза прямоугольного треугольника.
Скачать все формулы в формате Word
В данной публикации мы рассмотрим, каким образом можно посчитать периметр треугольника и разберем примеры решения задач.
- Формула вычисления периметра
- Примеры задач
Формула вычисления периметра
Периметр (P) любого треугольника равняется сумме длин всех его сторон.
P = a + b + c
Периметр равнобедренного треугольника
Равнобедренным называют треугольник, у которого две боковые стороны равны (примем их за b). Сторона a, имеющая отличную от боковых длину, является основанием. Таким образом, периметр можно считать так:
P = a + 2b
Периметр равностороннего треугольника
Равносторонним или правильным называется треугольник, у которого все стороны равны (примем ее за a). Периметр такой фигуры вычисляется так:
P = 3a
Примеры задач
Задание 1
Найдите периметр треугольника, если его стороны равны: 3, 4 и 5 см.
Решение:
Подставляем в формулу известные по условиям задачи величины и получаем:
P = 3 см + 4 см + 5 см = 12 см.
Задание 2
Найдите периметр равнобедренного треугольника, если его основание равняется 10 см, а боковая сторона- 8 см.
Решение:
Как мы знаем, боковые стороны равнобедренного треугольника равны, следовательно:
P = 10 см + 2 ⋅ 8 см = 26 см.

{P=a+b+c}
Чтобы найти периметр треугольника необходимо сложить длины трех его сторон. Однако, существует множество других формул, которые позволяют рассчитать периметр треугольника. На странице мы собрали самые известные формулы для расчета периметра треугольника, а также удобный калькулятор.
Содержание:
- калькулятор периметра треугольника
- формула периметра треугольника через стороны
- формула периметра треугольника по средним линиям
- формула периметра треугольника по двум сторонам и углу между ними
- формула периметра прямоугольного треугольника по катету и гипотенузе
- формула периметра прямоугольного треугольника по катетам
- формула периметра прямоугольного треугольника по гипотенузе и прилежащему углу
- формула периметра прямоугольного треугольника по катету и прилежащему углу
- формула периметра прямоугольного треугольника по катету и противолежащему углу
- формула периметра равнобедренного треугольника по боковой стороне и высоте
- формула периметра равнобедренного треугольника по основанию и высоте
- формула периметра равнобедренного треугольника по боковой стороне и основанию
- формула периметра равностороннего треугольника по высоте
- формула периметра равностороннего треугольника через площадь вписанной окружности
- примеры задач
Треугольник – геометрическая фигура, состоящая из трех точек, которые не лежат на одной прямой, и трех отрезков, которые попарно соединяют эти точки.
Формула периметра треугольника через стороны
{P = a+b+c}
a, b и c – стороны треугольника
Формула периметра треугольника по средним линиям
Средняя линия треугольника — отрезок, который соединяет середины двух сторон.
{P=2a+2b+2c}
a, b и c – средние линии треугольника
Формула периметра треугольника по двум сторонам и углу между ними
{P=a+b+sqrt{a^2+b^2-2ab cdot cos(alpha)}}
a и b – стороны треугольника
α – угол между сторонами a и b
Формула периметра прямоугольного треугольника по катету и гипотенузе
Прямоугольный треугольник — это треугольник, в котором один угол прямой (90 градусов).
{P = a+c+sqrt{c^2-a^2}}
a – катет прямоугольного треугольника
c – гипотенуза прямоугольного треугольника
Формула периметра прямоугольного треугольника по катетам
{P = a+b+sqrt{a^2+b^2}}
a и b – катеты прямоугольного треугольника
Формула периметра прямоугольного треугольника по гипотенузе и прилежащему углу
{P=csin(alpha)+ccos(alpha)+c}
c – гипотенуза прямоугольного треугольника
α – прилежащий к гипотенузе угол
Формула периметра прямоугольного треугольника по катету и прилежащему углу
{P=a \tg(alpha)+a+dfrac{a}{cos(alpha)}}
a – катет прямоугольного треугольника
α – прилежащий к катеру угол
Формула периметра прямоугольного треугольника по катету и противолежащему углу
{P=a+dfrac{a}{\tg(alpha)}+dfrac{a}{sin(alpha)}}
a – катет прямоугольного треугольника
α – противолежащий к катеру угол
Формула периметра равнобедренного треугольника по боковой стороне и высоте
Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине.
{P = 2a+2sqrt{a^2-h^2}}
a – боковая сторона равнобедренного треугольника
h – высота равнобедренного треугольника
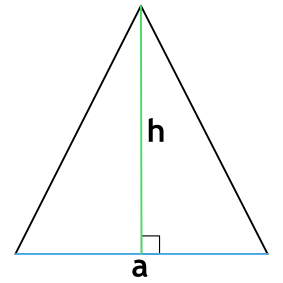
Формула периметра равнобедренного треугольника по основанию и высоте
{P = a+2sqrt{Big( Big(dfrac{a}{2} Big)^2+h^2 Big)}}
a – основание равнобедренного треугольника
h – высота равнобедренного треугольника
Формула периметра равнобедренного треугольника по боковой стороне и основанию
{P=2b+a}
a – основание равнобедренного треугольника
b – боковая сторона равнобедренного треугольника
Формула периметра равностороннего треугольника по высоте
Равносторонний треугольник —треугольник, у которого все стороны равны.
{P=2sqrt{3}h}
h – высота равностороннего треугольника
Формула периметра равностороннего треугольника через площадь вписанной окружности
{P = 6sqrt{dfrac{3S}{pi}}}
S – площадь вписанной в равносторонний треугольник окружности
Примеры задач на нахождение периметра треугольника
Задача 1
Найдите периметр треугольника, если его средние линии равны 6см 9см и 10см.
Решение
Для решения задачи применим формулу №2. Подставим в нее длины средних линий и произведем вычисления.
P = 2a+2b+2c = 2 cdot 6 + 2 cdot 9 + 2 cdot 10 = 12 + 18 + 20 = 50 : см
Ответ: 50 см
Ответ проверим с помощью калькулятора .
Задача 2
Найдите периметр треугольника со сторонами 14см, 17см и 17см.
Решение
А для этой задачи подойдет первая формула.
P = a+b+c = 14 + 17 + 17 = 48 : см
Если обратить внимание на то, что у треугольника в условии две стороны имеют одинаковую длину, то можно понять, что данный треугольник равнобедренный. И тогда задачу можно решить используя формулу для равнобедренного треугольника.
P=2b+a = 2 cdot 17 + 14 = 34 + 14 = 48 : см
Ответ: 48 см
Проверим ответ по первой и второй формуле.
Задача 3
Найдите периметр прямоугольного треугольника, если его катеты равны 12см и 16см.
Решение
Воспользуемся подходящей формулой.
P = a+b+sqrt{a^2+b^2} = 12+16+sqrt{12^2+16^2} = 28+sqrt{144+256} = 28+sqrt{400} = 28+20 = 48 : см
Ответ: 48 см
Полученный результат удобно проверить с помощью калькулятора .
Задача 4
Найдите периметр равнобедренного треугольника основание которого равно 13см а боковая сторона 8см.
Решение
Для равнобедренного треугольника, у которого известно основание и боковая сторона нам подходит эта формула.
P=2b+a = 2 cdot 8 + 13 = 16 + 13 = 29 : см
Ответ: 29 см
Проверка .
Задача 5
Найдите периметр равностороннего треугольника, если его высота равна 9см.
Решение
Для равностороннего треугольника с известной высотой мы применим эту формулу.
P = 2sqrt{3}h = 2sqrt{3} cdot 9 = 18sqrt{3} : см approx 31.17691 : см
Ответ: 18sqrt{3} : см approx 31.17691 : см
Проверить ответ поможет калькулятор .
Основные определения
Наверное, каждый из нас сталкивался с треугольником. Это могло быть в школе, вузах, колледжах, на работе, во время помощи детям. Треугольник – это одна из самых простых геометрических фигур, но в то же время она выполняет очень важную роль. Множество свойств хранит треугольник. Но сегодня не будем вдаваться в подробности, а поговорим про периметр и порешаем задачи по нахождению его.
Если мы отметим на плоскости 3 точки и проведём к ним линии, то как раз получим треугольник.
Понятия
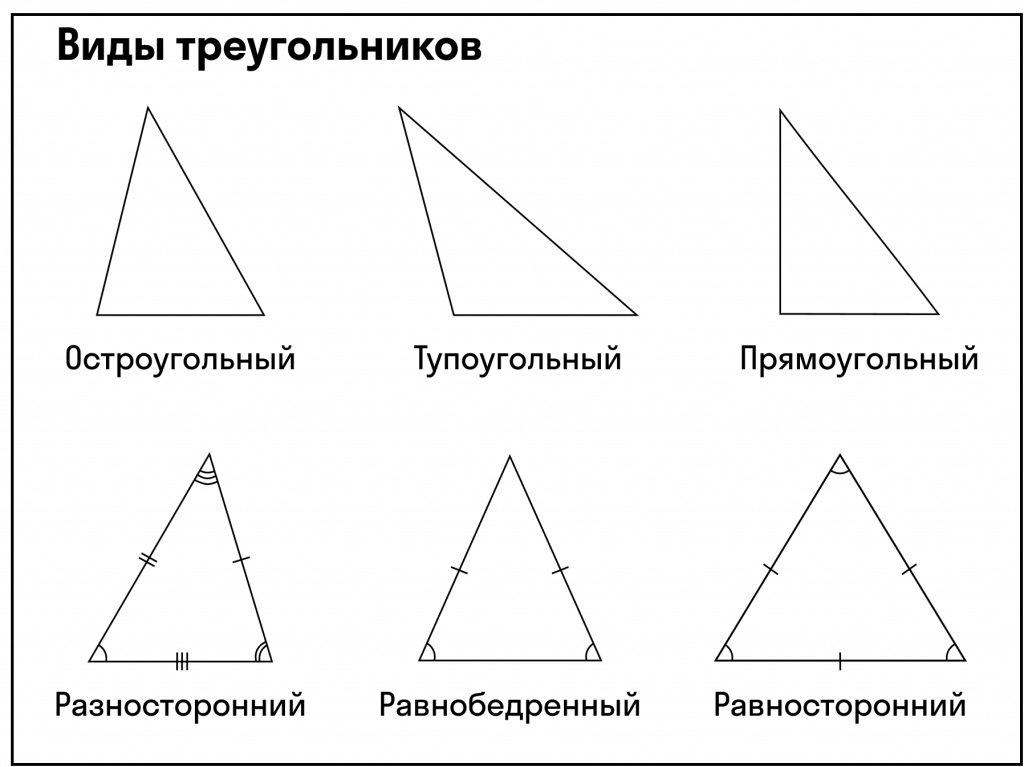
Треугольник – это геометрическая фигура, состоящая из трёх точек, которые соединены отрезками – сторонами. В зависимости от отношений между сторонами фигуры, то они бывают равносторонними, разносторонними и равнобедренными (р/б – равнобедренный, р/с – равносторонний).
Вершины треугольника – это точки, где соединяются 2 стороны фигуры.
Р/б треугольник – это треугольник у которого две стороны равны, но не равны третьей.
Р/с треугольник – это треугольник, у которого все стороны равны между собой.
Разносторонний треугольник – это треугольник, у которого все стороны не равны между собой.
Прямоугольный треугольник — это треугольник, у у которого один угол равен 90о. Самая длинная сторона называется гипотенузой, а две другие катетами.
Формула нахождения периметра
Из определения следует, что периметр геометрической фигуры – это сумма длин всех сторон, и треугольник не стал исключением. Общая формула имеет вид: Р = а + b + с. Периметр будет обозначаться Р. а, b и с — стороны треугольника. Решим задачу №1.
Задача 1
Пусть нам дан треугольник со сторонами 13 см, 15 см, 12 см. Нужно найти периметр данного треугольника.
Решение: [P=13+15+12=40] см.
Ответ: 40 см.
Периметр разностороннего треугольника
В прошлой задаче мы как раз нашли периметр разностороннего треугольника. Решим похожую задачу №2
Задача 2
Дан треугольник со сторонами 25 дм, 30 дм, 15 дм. Найдите периметр треугольника. Ответ выразите в метрах.
Решение:
P = 30 + 25 + 15 = 70 дм
70 : 10 = 7 м
Ответ: 7 м.
Периметр равнобедренного треугольника
Так как в р/б треугольнике 2 стороны равны (боковые), то формулу нахождения можно представить как: P = 2a + b. Решим 2 задачи.
Задачи 3 — 4
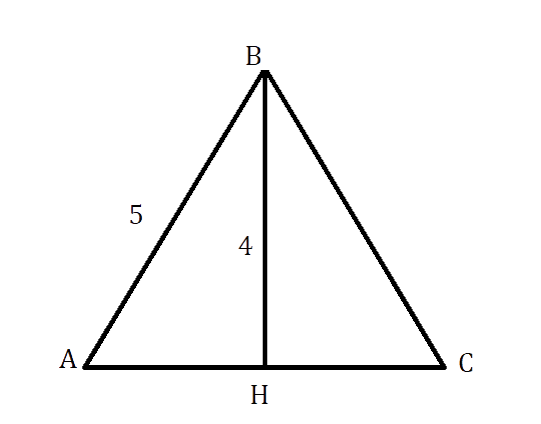
Дан равнобедренный треугольник АВС с биссектрисой, проведённой к основанию и равной 4 см, а также с боковой
стороной, равной 5 см. Найдите периметр данного треугольника.
Решение:
Так как ВН – биссектриса р/б треугольника АВС, то она является как высотой, так и медианой. Следовательно, ΔАВН прямоугольный и АН = НС.
В ΔАВН по теореме Пифагора [A H^{2}=A B^{2}-B H^{2}=25-16=9]см
АН = НС = √9 = 3 см
АС = АН + НС = 3 + 3 = 6 см
Р = 6 + 2*5 = 16 см
Ответ: 16 см.
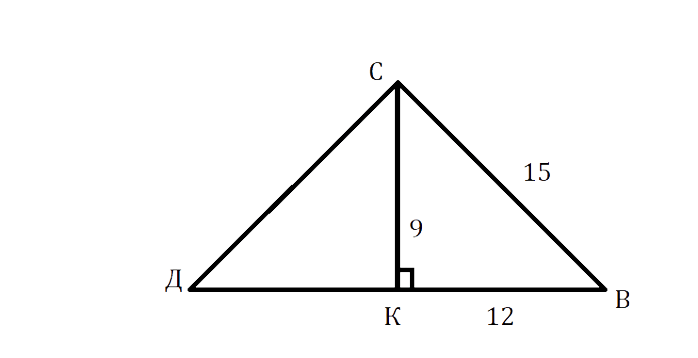
В треугольнике ДСВ ДС = СВ = 15 см, высота СК = 9 см. Найдите периметр этого треугольника.
Решение:
В ΔСКД по теореме Пифагора:
[text { ДК² }=text { ДС }^{2}-mathrm{CK}^{2}=225-81=144]см
ДК = √144 = 12 см.
Так как СК — высота в р/б треугольнике, проведённая к основанию, то она является медианой, следовательно, ДВ = ДК + КВ = 12 + 12 = 24 см.
Р = ДС + СВ + ДВ = 15 + 15 + 24 = 54 см.
Ответ: 54 см.
Нет времени решать самому?
Наши эксперты помогут!
Периметр равностороннего треугольника
А это один из самых “хороших” треугольников, его ещё называют правильным, так как все стороны и углы равны между собой. Формула нахождения периметра будет иметь вид: P = 3a.
Задачи 5 — 6
Дан равносторонний треугольник со стороной а = 13. Найдите периметр этого треугольника.
Решение:
Р = 3а = 3 * 13 = 39
Ответ: 39.
В равностороннем треугольнике АВС есть стороны: АВ = АС = СВ = 15 см, Найдите периметр данного треугольника.
Решение:
Р = 3АВ = 15 * 3 = 45 см.
Ответ: 45 см.
Периметр прямоугольного треугольника
Вычисляем по стандартной формуле: Р = а + в + с. Но у такого вида треугольников есть огромное преимущество – применение теоремы Пифагора.
Задачи 7 — 8
Дан прямоугольный треугольник с катетами а = 6 и в = 8. Найдите периметр.
Решение:
По теореме Пифагора: [c^{2}=в^{2}+a^{2}=64+36=100]
с = √100 = 10
Р = а + в + с = 6 + 8 + 10 = 24
Ответ: 24.
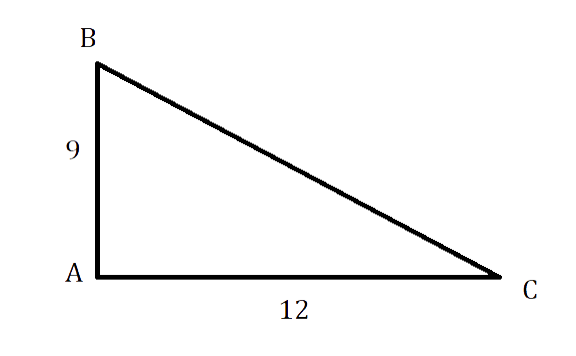
В прямоугольном треугольнике АВС, [angle mathrm{A}=90^{circ}, mathrm{AB}=9 mathrm{~см}, mathrm{AC} = 12см]. Надо найти периметр и площадь АВС.
Решение
По теореме Пифагора в ΔАВС:
[mathrm{CB}^{2}=mathrm{AC}^{2}+A mathrm{C}^{2}=144+81=225 mathrm{~см}]
СВ = √225 = 15 см
S = (АС * АВ) : 2 = (9 * 12) : 2 = 54 см
P = 15 + 9 + 12 = 36 см
Ответ: 36 см; 54 см.