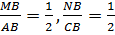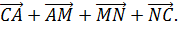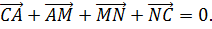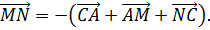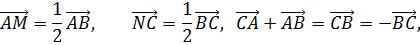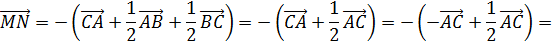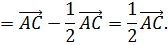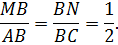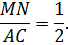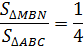Как найти среднюю линию треугольника?
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Понятие треугольника
Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, которые не лежат на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
- Прямоугольный. Один угол прямой, то есть равен 90 градусам, два других меньше 90 градусов.
- Остроугольный. Градусная мера всех углов больше 0, но меньше 90 градусов.
- Тупоугольный. Один угол тупой, два других — острые.
Треугольник считают равнобедренным, если две его стороны равны. Эти стороны называют боковыми сторонами, а третью — основанием.
Треугольник, у которого все стороны равны, называется равносторонним или правильным.
Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, которая лежит напротив прямого угла — гипотенуза, а две другие стороны — катеты.
Правильный (равносторонний или равноугольный) треугольник — это правильный многоугольник, в котором все стороны равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.
Свойства треугольников:
- В треугольнике против большего угла лежит большая сторона — и наоборот.
- Сумма углов треугольника равна 180 градусов.
- Все углы равностороннего треугольника равны 60 градусам.
- В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Понятие средней линии треугольника
Определение средней линии треугольника подходит для любого вида этой фигуры.
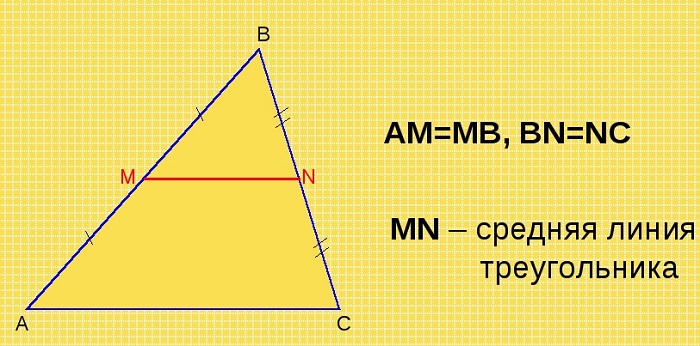
Средняя линия треугольника — отрезок, который соединяет середины двух сторон. В любом треугольнике можно провести три средних линии.
Основанием считается сторона, которой параллельна средняя линия.
Как найти среднюю линию треугольника — расскажем дальше, а для начала еще немного разберемся со всеми определениями.
Понятие средней линии прямоугольного треугольника
Математики говорят: в любом треугольнике можно провести три средних линии. В прямоугольном треугольнике этот отрезок будет равен половине основания — это и есть формула средней линии прямоугольного треугольника.
Прямой угол помогает нам применить другие признаки равенства и подобия. Для углов в прямоугольном треугольнике можно использовать геометрические тождества без дополнительных построений, а любую из сторон можно найти по теореме Пифагора.
В прямоугольном треугольнике две средние линии перпендикулярны катетам, а третья равна медиане, проведенной к гипотенузе. Средние линии острого и разностороннего треугольника не обладают подобными свойствами.
Свойства средней линии треугольника
Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.
Свойства:
- Средняя линия равна половине длины основания и параллельна ему.
- Средняя линия отсекает треугольник, подобный данному с коэффициентом 1/2; его площадь равна четверти площади данного.
- Три средние линии разделяют исходную фигуру на четыре равных треугольника. Центральный из них называют дополнительным.
- Три средние линии разделяют исходный прямоугольный треугольник на четыре равных прямоугольных треугольника.
Теорема о средней линии треугольника
Теорема о средней линии треугольника звучит так:
Средняя линия треугольника параллельна основанию и равна его половине. А так выглядит формула нахождения средней линии треугольника:
Докажем теорему:
По условию нам дано, что MA = MB, NA = NC
Рассмотрим два образовавшихся треугольника ΔAMN и ΔABC.
(по второму признаку подобия треугольников).
△ABC, то Следовательно, ВС = 2МN. Значит, доказано, что средняя линия равна половине основания.
△ABC, то ∠1 = ∠2 . Так как ∠1 и ∠2 — соответственные углы, то по признаку параллельности прямых MN || BC.
Параллельность средней линии и соответствующего ей основания доказана.
Пример 1. В треугольнике ΔABC AB = 8, BC = 7, CA = 5, точки M, K, N — середины сторон AB, BC, CA соответственно. Найти периметр ΔMNK.
Соединим середины сторон треугольника ΔABC и получим его средние линии, которые образуют треугольник ΔMNK. Найдем их длины по теореме о средней линии:
Ответ: периметр треугольника ΔMNK равен 10.
Пример 2. В прямоугольном треугольнике АВС есть две средние линии: MN и NP, равные 3 и 4 соответственно. Найти площадь большого прямоугольного треугольника.
Площадь треугольника равна половине произведения основания на высоту. Так как треугольник прямоугольный, то его площадь найдем как половину произведения катетов:
Так как MN — средняя линия, то по теореме о средней линии она равна половине катета AC:
Значит, AC = 2MN = 2 × 3 = 6.
Так как NP — средняя линия, то по теореме о средней линии она равна половине катета BC:
Значит, BC = 2NP = 2 × 4 = 8.
Тогда найдем площадь большого треугольника, используя формулу, указанную выше:
S = ½ × 6 × 8 = ½ × 48 = 24.
Ответ: площадь большого прямоугольного треугольника равна 24.
Средняя линия треугольника – свойства, признаки и формулы
Одним из важных понятий, с помощью которого легко решается целый класс задач по геометрии, является средняя линия треугольника.
Разберём данное понятие, рассмотрим свойства, и научимся правильно решать задачи на эту тему.
Определение и признаки средней линии треугольника
Отрезок, соединяющий середины двух сторон треугольника, называется его средней линией.
Отрезок, у которого один из концов совпадает с серединой одной из сторон, другой находится на второй стороне, проведённый параллельно третьей стороне, является средней линией треугольника.
Доказательство следует из теоремы Фалеса.
Теорема о средней линии треугольника
Средняя линия треугольника параллельна основанию (третьей стороне) и равна её половине.
Существует три вида доказательств этого положения. Каждое из них базируется на одной из ключевых позиций планиметрии.
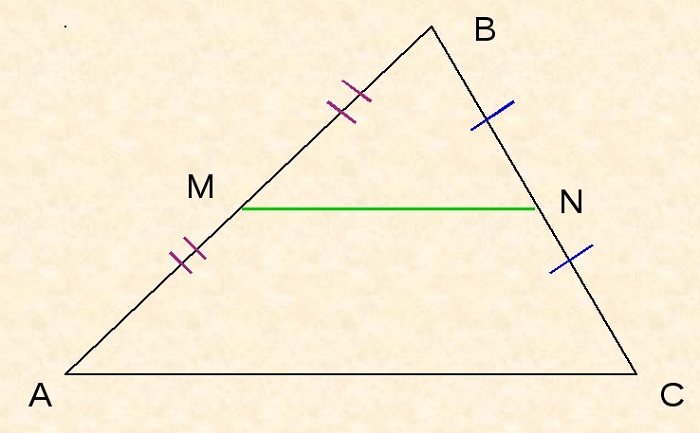
Пусть дан треугольник ABC, M – середина стороны AB, N – середина BC.
По определению, MN – средняя линия ΔABC.
Необходимо доказать, что MN II AC, MN = ½AC.
Доказательства
Пусть прямая MK II AC. Тогда по теореме Фалеса MK пересекает сторону BC в её середине. В этом случае отрезок MN лежит на прямой MK.
Следовательно, MN II AC.
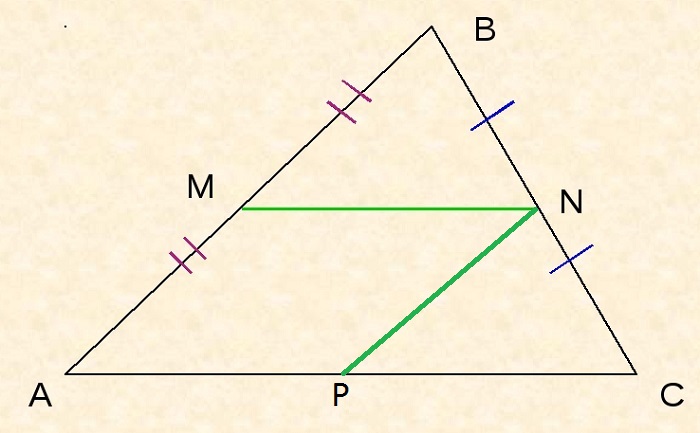
Тогда NP – средняя линия по теореме Фалеса, то есть AP = PC.
Так как AMNP – параллелограмм по определению, то AP = MN. Из этого и предыдущего утверждения следует, что длина MN равна ½AC.
Рассматриваются треугольники MBN и ABC. В них угол B является общим,
По второму признаку подобия треугольников ΔMBN ∼ ΔABC. Следовательно, углы BMN и BAC равны.
Поскольку эти углы являются соответственными, то прямые MN и AC параллельны.
Формула MN = ½AC следует из условий
поскольку пропорциональность двух пар сторон влечёт соответствующее отношение для третьей пары сторон.
Рассматривается сумма векторов
Поскольку в результате образуется замкнутая ломаная, то
Отсюда следует, что
Из последнего равенства следуют условия теоремы.
Следствия из теоремы с доказательствами
Следствие №1
Средняя линия отсекает треугольник, подобный данному, с коэффициентом подобия ½ и площадью, составляющий ¼ площади заданного треугольника.
По определению стороны AB и BC делятся пополам, поэтому
Из третьего признака подобия вытекает рассматриваемое свойство.
Поскольку площади подобных фигур относятся как квадрат коэффициента подобия, то получается вторая часть свойства, то есть площадь маленького треугольника относится к площади большого как
Следствие №2
Поскольку MN – средняя линия, то MN II AC, поэтому ∠BMN = ∠BAP, ∠BNM = ∠BCA как соответственные при MN II AC и секущей AB или BC соответственно.
Поскольку MP – средняя линия, то MP II BC, поэтому ∠MPA = ∠BCA как соответственные при MP II BC и секущей AC.
Таким образом: ∠BNM = ∠BCA = ∠MPA.
Так как MN – средняя линия, то сторона MN = ½AC, поэтому MN = AP.
Следовательно, ΔAMP = ΔMBN по второму признаку равенства треугольников.
Равенство остальных пар треугольников доказывается аналогично.
По основному свойству ΔMBN ∼ ΔABC с коэффициентом подобия ½. Так как все полученные маленькие треугольники равны между собой, то каждый из них, следовательно, подобен большому с тем же коэффициентом.
Свойства средней линии треугольника
Теорема и следствия из неё составляют основные свойства средней линии треугольника.
Согласно второму утверждению, вид большого треугольника такой же, как и у маленьких. То есть для равностороннего и равнобедренного треугольников средние линии отсекают равносторонние и равнобедренные треугольники.
Высоты тупоугольного треугольника, проведённые к тупому углу из вершин острых, располагаются вне треугольника. Поэтому часто рассматривают не саму среднюю линию, а её продолжение. Учитывая подобие получаемых фигур, можно утверждать, что точкой пересечения с продолжением средней линии высота делится на две равные части.
Биссектриса угла треугольника точкой пересечения со средней линией также делится пополам.
Средняя линия прямоугольного треугольника
Для прямоугольного треугольника две средние линии перпендикулярны катетам, а третья равна медиане, проведённой к гипотенузе.
Остроугольный разносторонний треугольник не имеет средних линий, обладающих подобными характеристиками.
Пример решения задачи
Доказать, что середины сторон произвольного выпуклого четырёхугольника являются вершинами параллелограмма.
Проводя диагональ четырёхугольника, получают разбиение на два треугольника, в каждом из которых построена средняя линия, параллельная по основной теореме диагонали, как основанию.
Так как две прямые, параллельные третьей, параллельны между собой, то противолежащие стороны образованного средними линиями четырёхугольника параллельны.
Аналогично доказывается параллельность двух других сторон нового четырёхугольника. По определению четырёхугольник, полученный соединением середин сторон заданного четырёхугольника, является параллелограммом.
Что такое средняя линия треугольника
В данной публикации мы рассмотрим определение, свойства и признак средней линии треугольника, а также разберем пример решения задачи для лучшего понимания теоретического материала.
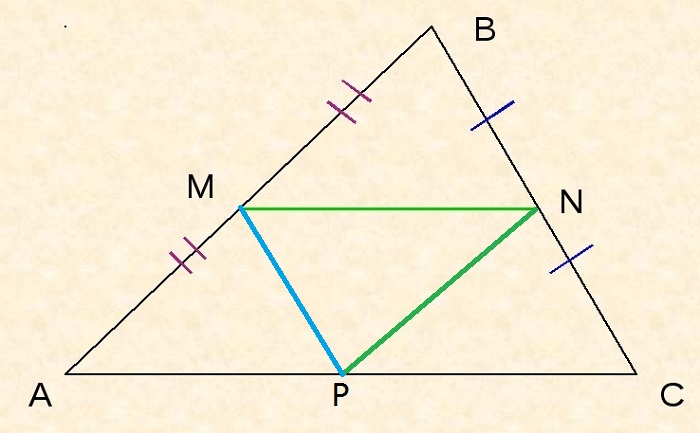
Определение средней линии треугольника
Отрезок, который соединяет середины двух сторон треугольника, называется его средней линией.
- KL – средняя линия треугольника ABC
- K – середина стороны AB: AK = KB
- L – середина стороны BC: BL = LC
Свойства средней линии треугольника
Свойство 1
Средняя линия треугольника параллельна одной из его сторон (которую не пересекает) и в два раза меньше этой стороны.
На рисунке выше:
Свойство 2
Средняя линия треугольника отсекает от него подобный треугольник (в соотношении 1:2), площадь которого в 4 раза меньше исходного.
На рисунке выше:
- △KBL ∼ △ABC (подобие по пропорциональности всех сторон)
- Стороны △KBL в два раза меньше соответствующих сторон △ABC:
AB = 2KB, BC = 2BL, AC = 2KL. - S△ABC = 4 ⋅ S△KBL
Свойство 3
В любом треугольнике можно провести три средние линии.
KL, KM и ML – средние линии треугольника ABC.
Свойство 4
Три средние линии треугольника делят его на 4 равных по площади треугольника.
Признак средней линии треугольника
Отрезок, проходящий через середину одной из сторон треугольника, пресекающий вторую и параллельный третьей стороне, является средней линией этого треугольника.
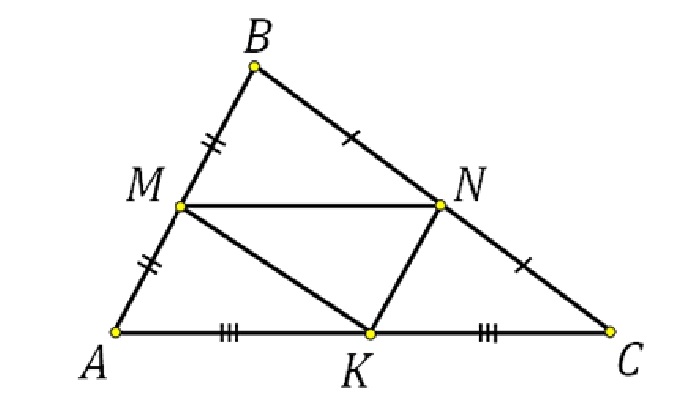
Пример задачи
Дан треугольник, две стороны которого равны 6 и 8 см. Найдите длину средней линии, соединяющей эти стороны.
Треугольник с заданными сторонами является прямоугольным, причем известные значения – это длины катетов. Средняя линия, которая соединяет катеты, параллельна гипотенузе и равна половине ее длины.
Мы можем найти гипотенузу, воспользовавшись теоремой Пифагора.
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
BC = 10.
Таким образом, средняя линия LM = 1 /2 ⋅ BC = 1 /2 ⋅ 10 = 5.
[spoiler title=”источники:”]
http://nauka.club/matematika/geometriya/srednyaya-liniya-treugolnika.html
[/spoiler]

{P=a+b+c}
Чтобы найти периметр треугольника необходимо сложить длины трех его сторон. Однако, существует множество других формул, которые позволяют рассчитать периметр треугольника. На странице мы собрали самые известные формулы для расчета периметра треугольника, а также удобный калькулятор.
Содержание:
- калькулятор периметра треугольника
- формула периметра треугольника через стороны
- формула периметра треугольника по средним линиям
- формула периметра треугольника по двум сторонам и углу между ними
- формула периметра прямоугольного треугольника по катету и гипотенузе
- формула периметра прямоугольного треугольника по катетам
- формула периметра прямоугольного треугольника по гипотенузе и прилежащему углу
- формула периметра прямоугольного треугольника по катету и прилежащему углу
- формула периметра прямоугольного треугольника по катету и противолежащему углу
- формула периметра равнобедренного треугольника по боковой стороне и высоте
- формула периметра равнобедренного треугольника по основанию и высоте
- формула периметра равнобедренного треугольника по боковой стороне и основанию
- формула периметра равностороннего треугольника по высоте
- формула периметра равностороннего треугольника через площадь вписанной окружности
- примеры задач
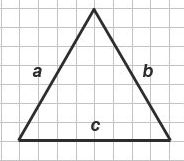
Треугольник – геометрическая фигура, состоящая из трех точек, которые не лежат на одной прямой, и трех отрезков, которые попарно соединяют эти точки.
Формула периметра треугольника через стороны
{P = a+b+c}
a, b и c – стороны треугольника
Формула периметра треугольника по средним линиям
Средняя линия треугольника — отрезок, который соединяет середины двух сторон.
{P=2a+2b+2c}
a, b и c – средние линии треугольника
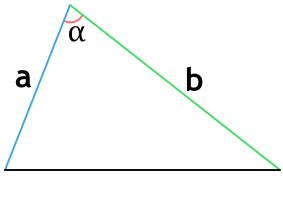
Формула периметра треугольника по двум сторонам и углу между ними
{P=a+b+sqrt{a^2+b^2-2ab cdot cos(alpha)}}
a и b – стороны треугольника
α – угол между сторонами a и b
Формула периметра прямоугольного треугольника по катету и гипотенузе
Прямоугольный треугольник — это треугольник, в котором один угол прямой (90 градусов).
{P = a+c+sqrt{c^2-a^2}}
a – катет прямоугольного треугольника
c – гипотенуза прямоугольного треугольника
Формула периметра прямоугольного треугольника по катетам
{P = a+b+sqrt{a^2+b^2}}
a и b – катеты прямоугольного треугольника
Формула периметра прямоугольного треугольника по гипотенузе и прилежащему углу
{P=csin(alpha)+ccos(alpha)+c}
c – гипотенуза прямоугольного треугольника
α – прилежащий к гипотенузе угол
Формула периметра прямоугольного треугольника по катету и прилежащему углу
{P=a \tg(alpha)+a+dfrac{a}{cos(alpha)}}
a – катет прямоугольного треугольника
α – прилежащий к катеру угол
Формула периметра прямоугольного треугольника по катету и противолежащему углу
{P=a+dfrac{a}{\tg(alpha)}+dfrac{a}{sin(alpha)}}
a – катет прямоугольного треугольника
α – противолежащий к катеру угол
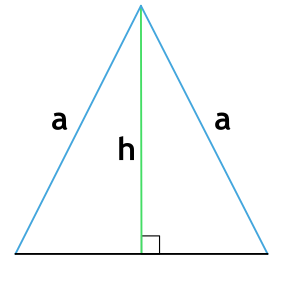
Формула периметра равнобедренного треугольника по боковой стороне и высоте
Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине.
{P = 2a+2sqrt{a^2-h^2}}
a – боковая сторона равнобедренного треугольника
h – высота равнобедренного треугольника
Формула периметра равнобедренного треугольника по основанию и высоте
{P = a+2sqrt{Big( Big(dfrac{a}{2} Big)^2+h^2 Big)}}
a – основание равнобедренного треугольника
h – высота равнобедренного треугольника
Формула периметра равнобедренного треугольника по боковой стороне и основанию
{P=2b+a}
a – основание равнобедренного треугольника
b – боковая сторона равнобедренного треугольника
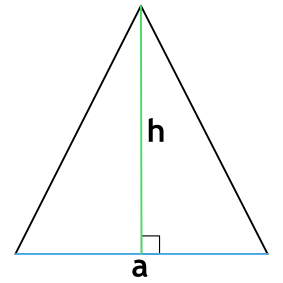
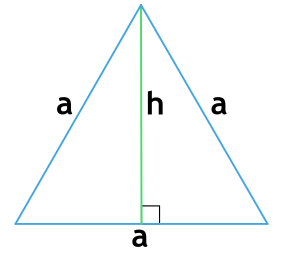
Формула периметра равностороннего треугольника по высоте
Равносторонний треугольник —треугольник, у которого все стороны равны.
{P=2sqrt{3}h}
h – высота равностороннего треугольника
Формула периметра равностороннего треугольника через площадь вписанной окружности
{P = 6sqrt{dfrac{3S}{pi}}}
S – площадь вписанной в равносторонний треугольник окружности
Примеры задач на нахождение периметра треугольника
Задача 1
Найдите периметр треугольника, если его средние линии равны 6см 9см и 10см.
Решение
Для решения задачи применим формулу №2. Подставим в нее длины средних линий и произведем вычисления.
P = 2a+2b+2c = 2 cdot 6 + 2 cdot 9 + 2 cdot 10 = 12 + 18 + 20 = 50 : см
Ответ: 50 см
Ответ проверим с помощью калькулятора .
Задача 2
Найдите периметр треугольника со сторонами 14см, 17см и 17см.
Решение
А для этой задачи подойдет первая формула.
P = a+b+c = 14 + 17 + 17 = 48 : см
Если обратить внимание на то, что у треугольника в условии две стороны имеют одинаковую длину, то можно понять, что данный треугольник равнобедренный. И тогда задачу можно решить используя формулу для равнобедренного треугольника.
P=2b+a = 2 cdot 17 + 14 = 34 + 14 = 48 : см
Ответ: 48 см
Проверим ответ по первой и второй формуле.
Задача 3
Найдите периметр прямоугольного треугольника, если его катеты равны 12см и 16см.
Решение
Воспользуемся подходящей формулой.
P = a+b+sqrt{a^2+b^2} = 12+16+sqrt{12^2+16^2} = 28+sqrt{144+256} = 28+sqrt{400} = 28+20 = 48 : см
Ответ: 48 см
Полученный результат удобно проверить с помощью калькулятора .
Задача 4
Найдите периметр равнобедренного треугольника основание которого равно 13см а боковая сторона 8см.
Решение
Для равнобедренного треугольника, у которого известно основание и боковая сторона нам подходит эта формула.
P=2b+a = 2 cdot 8 + 13 = 16 + 13 = 29 : см
Ответ: 29 см
Проверка .
Задача 5
Найдите периметр равностороннего треугольника, если его высота равна 9см.
Решение
Для равностороннего треугольника с известной высотой мы применим эту формулу.
P = 2sqrt{3}h = 2sqrt{3} cdot 9 = 18sqrt{3} : см approx 31.17691 : см
Ответ: 18sqrt{3} : см approx 31.17691 : см
Проверить ответ поможет калькулятор .
Одной из базовых геометрических фигур является треугольник. Он образуется при пересечении трех отрезков прямых. Данные отрезки прямых формируют стороны фигуры, а точки их пересечения называются вершинами. Каждый школьник, изучающий курс геометрии, обязан уметь находить периметр этой фигуры. Полученное умение будет полезным для многих и во взрослой жизни, к примеру, пригодится студенту, инженеру, строителю, дизайнеру.
Существуют разные способы найти периметр треугольника. Выбор необходимой для вас формулы зависит от имеющихся исходных данных. Чтобы записать данную величину в математической терминологии используют специальное обозначение – Р. Рассмотрим, что такое периметр, основные способы его расчета для треугольных фигур разных видов.
Классическая формула
Самым простым способом найти периметр фигуры, если есть данные всех сторон. В этом случае используется следующая формула:
P = a + b + c.
Буквой «P» обозначается сама величина периметра. В свою очередь «a», «b» и «c» – это длины сторон.
Зная размер трех величин, достаточно будет получить их сумму, которая и является периметром.
Это интересно! Что значит вертикально и как выглядит вертикальная линия
Альтернативный вариант
В математических задачах все данные длины редко бывают известны. В таких случаях рекомендуется воспользоваться альтернативным способом поиска нужной величины. Когда в условиях указана длина двух прямых, а также угол, находящийся между ними, расчет производится через поиск третьей. Для поиска этого числа необходимо добыть квадратный корень по формуле:
.
Далее рассчитывайте Р по такой формуле:
.
Периметр по двум сторонам
Для расчета периметра не обязательно знать все данные геометрической фигуры. Рассмотрим способы расчета по двум сторонам.
Это интересно! Основы геометрии: что это такое биссектриса треугольника
Равнобедренный треугольник
Равнобедренным называется такой треугольник, не меньше двух сторон которого имеют одинаковую длину. Они называются боковыми, а третья сторона – основанием. Равные прямые образовывают вершинный угол. Особенностью в равнобедренном треугольнике является наличие одной оси симметрии. Ось – вертикальная линия, выходящая из вершинного угла и заканчивающаяся посредине основания. По своей сути ось симметрии включает в себя такие понятия:
- биссектриса вершинного угла,
- медиана к основанию,
- высота треугольника,
- срединный перпендикуляр.
Чтобы определить периметр равнобедренного вида треугольной фигуры, воспользуйтесь формулой.
P = 2a + b.
В данном случае вам необходимо знать только две величины: основание и длину одной стороны. Обозначение «2а» подразумевает умножение длины боковой стороны на 2. К полученной цифре нужно добавить величину основания – «b».
В исключительном случае, когда длина основания равнобедренного треугольника равна его боковой прямой, можно воспользоваться более простым способом. Проведите досуг в расположении соблазнительной индивидуалки Тюмени . Посетите наш сайт, и вы найдёте коллекцию максимально талантливых девушек собственного района. просмотрите все имеющиеся варианты, и мы поможем вам в выборе подходящей партнёрши! Он выражается в следующей формуле:
P = 3a.
Для получения результата достаточно умножить это число на три. Эта формула используется для того, чтобы найти периметр правильного треугольника.
Это интересно! Изучаем символы: как обозначается в математике площадь
Полезное видео: задачи на периметр труегольника
Треугольник прямоугольный
Главным отличием прямоугольного треугольника от других геометрических фигур этой категории является наличие угла 90°. По этому признаку и определяется вид фигуры. Прежде, чем определить, как найти периметр прямоугольного треугольника, стоит заметить, что данная величина для любой плоской геометрической фигуры составляет сумму всех сторон. Так и в этом случае самый простой способ узнать результат – суммировать три величины.
В научной терминологии те стороны, которые прилегают к прямому углу, имеют название «катеты», а противоположная к углу 90º – гипотенуза. Особенности этой фигуры исследовались еще древнегреческим ученым Пифагором. Согласно с теоремой Пифагора, квадрат гипотенузы равен сумме квадратов катетов.
.
На основании данной теоремы выведена еще одна формула, объясняющая, как найти периметр треугольника по двум известным сторонам. Рассчитать периметр при указанной длине катетов можно, используя следующий способ.
.
Чтобы узнать периметр, имея информацию о размере одного катета и гипотенузы, нужно определить длину второй гипотенузы. С этой целью используют такие формулы:
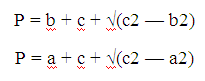
Также периметр описанного вида фигуры определяется и без данных о размерах катетов.
.
Вам потребуется знать длину гипотенузы, а также угол, прилегающий к ней. Зная длину одного из катетов, если имеется угол, прилегающий к нему, периметр фигуры рассчитывают по формуле:
.
Это интересно! Как найти и чему будет равна длина окружности
Расчет через высоту
Рассчитать периметр таких категорий, как равнобедренные и прямоугольные треугольники, можно через показатель их средней линии. Как известно, высота треугольника разделяет его основание пополам. Таким образом, она образует две прямоугольных фигуры. Далее, нужный показатель вычисляется при помощи теоремы Пифагора. Формула будет иметь следующий вид:
.
Если известна высота и половина основания, используя этот способ, вы получите нужное число без поиска остальных данных о фигуре.
Полезное видео: нахождение периметра треугольника
Как найти периметр треугольника зная его среднюю линию?
Если вам необходимо получить ответ на вопрос Как найти периметр треугольника зная его среднюю линию?, относящийся
к уровню подготовки учащихся 10 – 11 классов, вы открыли нужную страницу.
В категории Геометрия вы также найдете ответы на похожие вопросы по
интересующей теме, с помощью автоматического «умного» поиска. Если после
ознакомления со всеми вариантами ответа у вас остались сомнения, или
полученная информация не полностью освещает тематику, создайте свой вопрос с
помощью кнопки, которая находится вверху страницы, или обсудите вопрос с
посетителями этой страницы.
Ответы Mail.ru
Домашние задания
Русский язык
Литература
Математика
Алгебра
Геометрия
Иностранные языки
Химия
Физика
Биология
История
Обществознание
География
Информатика
Экономика
Другие предметы
Вопросы – лидеры.
Помогите пожалуйста! СРОЧНО!!!!!
Сделайте развёрнуто и кратко.
1 ставка
Решите пожалуйста задачу
1 ставка
Просьба оказать помощь в решении задачи
1 ставка
Помогите пожалуйста,очень срочно нужно выполнить
1 ставка
Лидеры категории
Лена-пена
Искусственный Интеллект
М.И.
Искусственный Интеллект
Y.Nine
Искусственный Интеллект
•••
Как найти периметр треугольника если даны средние линии?
Алена Сущенко
Ученик
(95),
на голосовании
13 лет назад
Голосование за лучший ответ
Мастер Гармонии
Мыслитель
(5359)
13 лет назад
сложить величины средних линий и умножить на два.
Похожие вопросы