|
Как находить периметр геометрических фигур (треугольник, четырёхугольник, многоугольник) по известным координатам вершин? Какая формула должна использоваться? Формула для вычисления длины стороны АВ по известным координатам:
Аналогичным образом высчитываются остальные стороны, а затем полученные величины суммируются. автор вопроса выбрал этот ответ лучшим
Ксарфакс 4 года назад Периметр по координатам Периметр фигуры – это сумма длин всех её сторон. Чтобы в нашем случае найти длины сторон, нужно воспользоваться формулой длины отрезка по заданным координатам (x1; y1) и (x2; y2):
Последовательно складываем все полученные значения и получаем периметр. Если в задаче вид фигуры (квадрат, прямоугольник, равносторонний треугольник и т.п.) оговаривается заранее, то находить все длины может и не понадобиться. Например, периметр квадрата ABCD будет равен 4 * AB, так как у этой фигуры все стороны равны. То есть будет достаточно вычислить, чему равна сторона AB и умножить её на 4. Рассмотрим несколько примеров. 1) Треугольник ABC имеет координаты A(1,1); B(1,3); C(2,1). P(ABC) = AB + AC + BC. AB = √(0 + 2²) = √4 = 2. AC = √(1² + 0) = √1 = 1. BC = √(1² + (-2)²) = √5 ≈ 2,24. Таким образом, P(ABC) ≈ 2 + 1 + 2,24 = 5,24. 2) Прямоугольник ABCD имеет координаты A(2,1); B(2,4); C(3,4); C(3,1). P(ABCD) = 2AB + 2BC (так как по определению прямоугольника AB = CD и BC = AD). AB = √(0 + 3²) = √9 = 3. AC = √(1² + 0) = √1 = 1. Таким образом, P(ABC) = 3 * 2 + 1 * 2 = 8. ** Найти периметр по координатам можно и без использования формулы длины отрезка. Порядок действий такой:
Sadness 4 года назад Так как координаты вершин нам известны, то, для нахождения периметра, остаётся просто вычислить длину каждой стороны и сложить их. Длина отрезка вычисляется так:l=sqrt((x2 – x1)^2 + (y2 – y1)^2); Важно: вычитаем всегда начало из конца. Нахождение на примере:
Найдём длины всех трёх сторон и сложим. AB=sqrt((x2 – x1)^2 + (y2 – y1)^2)=sqrt((12 – 1)^2 + ((-5) – 8)^2)=sqrt(121 + 169)=sqrt(290); BC=sqrt((x2 – x1)^2 + (y2 – y1)^2)=sqrt((-2 – 12)^2 + (1 – -(5))^2)=sqrt(196 + 36)=sqrt(232); CA=sqrt((1 – (-2))^2 + (8 – 1)^2)=sqrt(9 + 49)=sqrt(58); Далее просто складываем полученные результаты: P=AB+BC+CA; Ну вот и всё, так просто находится периметр по заданным координатам(для любой фигуры). P.s извиняюсь за плохо подобранные координаты.
Давайте сначала вспомним, что такое периметр фигуры и как его вычислить. Периметром называется сумма длин всех сторон данной фигуры. Таким образом, для вычисления периметра какой-либо фигуры нужно знать длину всех ее сторон. Затем дело останется за малым – просто сложить длины. По сути, сторона любого многоугольника ( треугольника, четырехугольника, пятиугольника и так далее ) представляется собой отрезок. Для вычисления длины отрезка по координатом его концов используется следующая формула:
, где х1 и х2 – координаты концов отрезка по оси х, а y1 и y2 – координаты по оси у. Подставляем в формулу значения, проводим вычисления. Находим длину каждой из сторон. Суммируем все длины.
Hamster1337 2 года назад Периметр геометрических фигур по координатам вершин можно найти при помощи формулы
Где x1,x2 это первая координата, y1,y2 это вторая координата. Данную формулу нужно применять к каждой паре соседних вершин многоугольника. После обхода и суммирования всех длин будет получен периметр.
Алиса в Стране 3 года назад Любая геометрическая фигура это совокупность отрезков, составляющих ее стороны, и вершин а ее периметр – сумма длин этих отрезков, сумма сторон, поэтому если мы найдем длины всех сторон и сложим их, то получим как раз периметр фигуры. Для того, чтобы найти длину отрезка АВ, зная его координаты, есть такая вот формула:
где точка А имеет координаты (x1; y1), а точка В – координаты (x2; y2). Итак, длину отрезка мы находить научились. Допустим теперь, что у нас есть треугольник АВС, мы знаем координаты его вершин, по указанной выше формуле мы находим длины отрезков АВ, ВС, АС и складываем их, получая периметр этого треугольника АВС: АВ + ВС + АС.
габбас 4 года назад Периметр любого многоугольника вычисляется как сумма длин всех его сторон. Значит задача сводится к нахождению длины отрезка по координатам его концов. А это известная формула из курса геометрии основной школы. Итак, длина отрезка d = sqrt(x2^2 – x1^2) + (y2^2 – y1^2), х1 и у1 координаты начала, х2,у2 – координаты конца отрезка. Таким образом находим длины всех сторон многоугольника и суммируем эти значения. Лара Изюминка 3 года назад Во-первых, вспомним, что такое периметр – это сумма длин сторон. То есть нам нужны длины сторон многоугольника. Чтобы их найти, зная координаты точек, воспользуемся формулой из геометрии для нахождения расстояния между двумя точками на плоскости: AB = √(xb – xa)2 + (yb – ya)2. То есть нужно вычислить корень квадратный из суммы квадратов разницы координат по х и по у. Если фигура в пространстве, то добавится еще разница координат по z. AB = √(xb – xa)2 + (yb – ya)2 + (zb – za)2 Когда длины всех отрезков найдем остается их только сложить. Периметром фигуры зовется сумма длин всех сторон. Для поиска длинны сторон воспользуйтесь формулой длинны отрезка согласно координатам, которые заданы. (x1; y1) и (x2; y2):
Так, если вы последовательно сложите значения, которые получите, то сможете получить периметр. Что касается примеров, при условии наличия координат по точкам А (4;2), В(-6;-3), С(0;8) Следует сложить – получить.
Бекки Шарп 3 года назад Если геометрическая фигура находится в системе координат и координаты ее вершин известны, то длину сторон будем искать по такой формуле:
У нас есть треугольник. Координаты его точек- А (4;2), В(-6;-3), С(0;8) Находим длины отрезков АВ, ВС и АС по формуле.
Складываем полученные результаты и получаем периметр.
Бархатные лапки 3 года назад Существует формула, по которой можно вычислить длину отрезка, если известны координаты. Делим нашу геометрическую фигуру на отрезки, считаем длину каждого отрезка и затем все значения длин складываем. Таким образом мы получаем периметр.
Знаете ответ? |
Как найти периметр треугольника, заданного координатами своих вершин
Периметр – это длина линии, ограничивающей занимаемую плоской геометрической фигурой площадь. Для треугольника, как и всех других многоугольников, это ломаная линия, составленная из его всех его сторон. Поэтому задача вычисления периметра треугольника, заданного координатами его вершин, сводится к вычислению длины каждой из сторон с последующим суммированием полученных величин.
Инструкция
Чтобы вычислить длину стороны, рассмотрите вспомогательный треугольник, составленный из самой стороны и двух ее проекций на оси абсцисс и ординат. В этой фигуре две проекции будут образовывать прямой угол – это вытекает из определения прямоугольных координат. Это означает, что они будут катетами в прямоугольном треугольнике, где гипотенузой будет сама сторона. Ее длину можно вычислить по теореме Пифагора, надо лишь найти длины проекций (катетов). Каждая из проекций представляет собой отрезок, начальная точка которого определена меньшей координатой, конечная – большей, а их разница и будет длиной проекции.
Рассчитайте длину каждой стороны. Если обозначить координаты точек, определяющих треугольник, как A(X₁,Y₁), B(X₂,Y₂) и C(X₃,Y₃), то для стороны АВ проекции на оси абсцисс и ординат будут иметь длины X₂-X₁ и Y₂-Y₁, а длина самой стороны в соответствии с теоремой Пифагора будет равна АВ = √((X₂-X₁)² + (Y₂-Y₁)²). Длины двух других сторон, рассчитанные через их проекции на оси координат, можно записать так: ВС = √(( X₃-X₂)² + (Y₃-Y₂)²), СА = √((X₃-X₁)² + (Y₃-Y₁)²).
При использовании трехмерной системы координат в подкоренное выражение, полученное на предыдущем шаге, добавьте еще одно слагаемое, которое должно выражать квадрат длины проекции стороны на ось аппликат. В этом случае координаты точек можно записать так: A(X₁,Y₁,Z₁), B(X₂,Y₂,Z₂) и C(X₃,Y₃,Z₃). А формулы расчета длин сторон примут такой вид: АВ = √((X₂-X₁)² + (Y₂-Y₁)² + (Z₂- Z₁)²), ВС = √(( X₃-X₂)² + (Y₃-Y₂)² + (Z₃-Z₂)²) и СА = √((X₃-X₁)² + (Y₃-Y₁)² + (Z₃-Z₁)²).
Рассчитайте периметр (Р) треугольника, сложив полученные на предыдущих шагах длины сторон. Для плоской Декартовой системы координат формула в общем виде должна выглядеть так: Р = АВ + ВС + СА = √((X₂-X₁)² + (Y₂-Y₁)²) + √(( X₃-X₂)² + (Y₃-Y₂)²) + √((X₃-X₁)² + (Y₃-Y₁)²). Для трехмерных координат эта же формула должна иметь такой вид: Р = √((X₂-X₁)² + (Y₂-Y₁)² + (Z₂- Z₁)²) + √(( X₃-X₂)² + (Y₃-Y₂)² + (Z₃-Z₂)²) + √((X₃-X₁)² + (Y₃-Y₁)² + (Z₃-Z₁)²).
Источники:
- площадь треугольника заданного координатами вершин
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Как найти периметр треугольника
Решение.
1) Координаты векторов
Координаты векторов находим по формуле:
X = xj — xi; Y = yj — yi; Z = zj — zi
здесь X,Y,Z координаты вектора; xi, yi, zi — координаты точки Аi; xj, yj, zj — координаты точки Аj;
Например, для вектора AB
X = x2 — x1; Y = y2 — y1; Z = z2 — z1
X = 2-2; Y = 0-1; Z = 5-3
AB(0;-1;2)
AC(3;-2;7)
BC(3;-1;5)
2) Модули векторов
Длина вектора a(X;Y;Z) выражается через его координаты формулой: 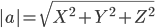
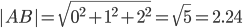
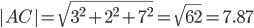
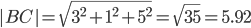
т.е. периметр равен Р = 2.236 + 7.874 + 5.916 =16.026.
ПОМОГИТЕ МНЕ ПОЖАЛУЙСТА. По координатам вершин треугольника ABC найти: периметр треугольника; уравнения сторон AB и BC; уравнение высоты AD; угол ABC; площадь треугольника. Сделать чертеж.
А(3; 3); В(–3; –3); С(3; 5).

Даны координаты вершин треугольника ABC: А(3; 3); В(–3; –3); С(3; 5).
1) Периметр треугольника.
Расчет длин сторон
АВ (с) = √((Хв-Ха)²+(Ув-Уа)²) = √72 = 6√2 ≈ 8,48528.
BC (а)= √((Хc-Хв)²+(Ус-Ув)²) = √100 = 10.
AC (в) = √((Хc-Хa)²+(Ус-Уa)²) = √4 = 2.
Периметр равен 12 + 6√2 ≈ 20,48528.
2) Уравнения сторон AB и BC.
х — у = 0 общее уравнение,
у = х уравнение с угловым коэффициентом (к = 1).
Хс-Хв Ус-Ув 6 8, сократить на 2:
у = (4/3)х + 1.
3) Уравнение высоты AD.
к(АД) = -1/к(ВС) = -1/(4/3) = -3/4.
у = (-3/4)х + в. Подставим точку А(3; 3): 3 = (-3/4)*3 + в, в = 3 + (9/4) = 21/4.
Уравнение АД: (-3/4)х + (21/4).
cos В= АВ²+ВС²-АС² = 0,98995.
B = 0,141897 радиан,
B = 8,130102 градусов.
5) Площадь S треугольника ABC равна:
Площадь можно найти по формуле Герона: S = √(p(p-a)(p-b)(p-c)).
Полупериметр p = 10,24264. S = 6.
6) Сделать чертеж — построить точки А, В и С по координатам и соединить отрезками.
Периметр многоугольника по его координатам
В данной статье мы окажем помощь в расчете периметра многоугольника, заданного координатами его вершин. Несмотря на то, что сам принцип расчета прост, при большом количестве вершин, Вам придется делать несколько раз одни и те же вычисления, то есть выполнять рутинную операцию. А я страсть как не люблю рутину и Вам ей заниматься не советую.
Формула которая используется проста:
Если извеcтны две точки с координатами (x1,y1) и (x2,y2) то расстояние между ними
эту формулу необходиом применить к каждой паре координат соседних вершин многоугольника. И как только мы закончим обход и просуммировав все длины мы получим наш периметр.
Теперь что касается ввода данных. В предыдущем материале Площадь многоугольника по координатам онлайн ввод координат осуществляется через двоеточие и пробел, что не совсем удобно.
В этой статье, для упрощения и для обощения ( на комплексное представление) коодинаты будут задаватся в виде комплексных чисел.
Для тех кто с комплексными числами никогда не сталкивался, хочу успокоить — ничего страшного.
И если Вы координату раньше представляли как (x,y), то в комплексном представлении эта же координата видится уже как x+iy
Для ввода это немного проще, так как в дальнейшем при написании статьи про линейные преобразования фигуры на плоскости, это форма ввода нам пригодится, да и понимать ту статью Вам будет уже намного проще.
Теперь немного примеров:
Определим периметр многоугольника заданного координатами А (0; 0); В (8; 2); С (–2; 6).
Так как три вершины то это треугольник.
Введем данные в поле ввода( разделяя каждую координату вершины пробелом) в таком формате 0+0i 8+2i -2+6i
�������
������� �������� ������������ ABC, ���� �������� ���������� ��� ������ A(–3, 5), B(3, –3) � ����� M(6, 1), ���������� ��������� ������� BC.
���������
�������������� ��������� ��� ��������� �������� ������� � ��������� ��� ���������� ����� ����� �������.
�������
����� (x, y) – ���������� ������� C. �� ������� ½ (x + 3) = 6, ½ (y – 3) = 1, ������ x = 9, y = 5.
�� ������� ���������� ����� ����� ������� ������� ������� ������������ ABC: AB = =
= 10,
BC = =
= 10, AC = 9 – (–3)) = 12. �������������, PABC = 10 + 10 + 12 = 32.
�����
32.
��������� � ���������� �������������
| web-���� | |
| �������� | ������� ����� �� ��������� �.�.������� |
| URL | http://zadachi.mccme.ru |
| ������ | |
| ����� | 4108 |













