Так как изначально периметр для любой фигуры – это сумма длин всех ее сторон, то периметр треугольника найти проще всего, зная все три стороны: P=a+b+c. Для равнобедренного треугольника формула периметра будет выглядеть несколько иначе в силу того, что две из сторон у него конгруэнтны, то есть равны по значению: P=2a+b. С равносторонним треугольником все еще незатейливей – у него все три стороны одинаковые, поэтому периметр будет равен утроенной стороне: P=3a.
Для треугольников, обладающих особыми свойствами, как например, вышеупомянутые равнобедренный и равносторонний треугольники, могут быть выведены и другие формулы. Например, периметр равнобедренного треугольника можно найти и через высоту. Высота в данном случае делит основание пополам, исходя из чего можно найти неизвестную сторону по теореме Пифагора из получившихся прямоугольных треугольников. Если дана боковая сторона, то половина основания будет равна  , а само основание, соответственно,
, а само основание, соответственно,  . Подставив его в формулу для нахождения периметра равнобедренного треугольника, получим
. Подставив его в формулу для нахождения периметра равнобедренного треугольника, получим  . Если дано основание, то по той же теореме Пифагора находим боковую сторону
. Если дано основание, то по той же теореме Пифагора находим боковую сторону  . Формула периметра равнобедренного треугольника через основание и высоту тогда принимает вид
. Формула периметра равнобедренного треугольника через основание и высоту тогда принимает вид  .
.
Найти периметр равностороннего треугольника становится возможным, уже зная одну лишь высоту. Используя теорему Пифагора, выражаем сторону треугольника через высоту  . Подставляем в формулу периметра равностороннего треугольника и получаем
. Подставляем в формулу периметра равностороннего треугольника и получаем 
Периметр прямоугольного треугольника можно найти, зная две стороны из трех. Если известны два катета a и b, то гипотенуза c по теореме Пифагора равна  , и периметр получается
, и периметр получается  . Если дана гипотенуза и один из катетов, формула периметра прямоугольного треугольника принимает уже другой вид:
. Если дана гипотенуза и один из катетов, формула периметра прямоугольного треугольника принимает уже другой вид: 
Как найти периметр треугольника

О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение
Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской буквой P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах и ходе решении.
Важно, чтобы все параметры были переданы в одной единице длины, иначе мы не сможем подсчитать результат. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
В чем измеряется периметр:
Как узнать периметр треугольника
Рассмотрим какие существуют формулы, и при каких известных исходных данных их можно применять.
Если известны три стороны, то периметр треугольника равен их сумме. Этот способ проходят во втором классе.
P = a + b + c, где a, b, c — длина стороны.
Если известна площадь и радиус вписанной окружности:
P = 2 * S : r, где S — площадь, r — радиус вписанной окружности.
Если известны две стороны и угол между ними, вычислить периметр треугольника можно так:
P = √ b 2 + с 2 – 2 * b * с * cosα + (b + с), где b, с — известные стороны, α — угол между известными сторонами.
Если известна одна сторона в равностороннем треугольнике:
P = 3 * a, где a — длина стороны.
Все стороны в равносторонней фигуре равны.
Если известна боковая сторона и основание в равнобедренном треугольнике:
P = 2 * a + b, где a — боковая сторона, b — основание.
Боковые стороны в равнобедренной фигуре равны.
Если известна боковая сторона и высота в равнобедренном треугольнике:
P = 2 * (√ a 2 + h 2 ) + 2 * a, где a — боковая сторона, h — высота.
Высотой принято называть отрезок, который вышел из вершины и опустился на основание. В равнобедренной фигуре высота делит основание пополам.
Если известны катеты в прямоугольном треугольнике:
P = √ a 2 + b 2 + (a + b), где a, b — катеты.
Катет — одна из двух сторон, которые образуют прямой угол.
Если известны катет и гипотенуза в прямоугольном треугольнике:
P = √ c 2 – a 2 + (a + c), где a — любой катет, c — гипотенуза.
Гипотенуза — сторона, которая лежит напротив прямого угла.
Скачать онлайн таблицу
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
Как посчитать периметр треугольника
Онлайн калькулятор
Периметр разностороннего треугольника
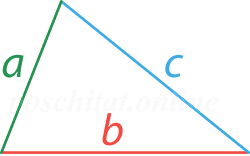
Чтобы вычислить чему равен периметр разностороннего треугольника вам нужно знать следующие параметры:
Введите их в соответствующие поля и узнаете чему равен периметр треугольника (Р).
Теория
Чему равен периметр разностороннего треугольника (P)?
Формула
Пример
К примеру, определим периметр разностороннего треугольника, у которого сторона a = 2 см, сторона b = 3 см, а сторона c = 4 см:
Периметр равнобедренного треугольника
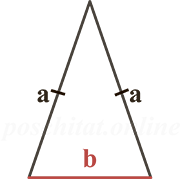
Чтобы вычислить чему равен периметр равнобедренного треугольника вам нужно знать следующие параметры:
- длину двух равных сторон (a)
- длину основания (b)
Теория
Чему равен периметр равнобедренного треугольника (P)?
Формула
Пример
К примеру, определим периметр равнобедренного треугольника, у которого стороны a = 2 см, а сторона b = 3 см:
Периметр равностороннего треугольника
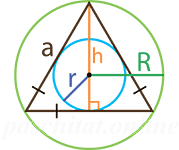
Чтобы вычислить чему равен периметр равностороннего треугольника вам нужно знать следующие параметры (либо-либо):
- длину трёх равных сторон (a)
- радиус описанной окружности (R)
- радиус вписанной окружности (r)
Урок геометрии: как найти по формуле периметр треугольника
Одной из базовых геометрических фигур является треугольник. Он образуется при пересечении трех отрезков прямых. Данные отрезки прямых формируют стороны фигуры, а точки их пересечения называются вершинами. Каждый школьник, изучающий курс геометрии, обязан уметь находить периметр этой фигуры. Полученное умение будет полезным для многих и во взрослой жизни, к примеру, пригодится студенту, инженеру, строителю, дизайнеру.
Существуют разные способы найти периметр треугольника. Выбор необходимой для вас формулы зависит от имеющихся исходных данных. Чтобы записать данную величину в математической терминологии используют специальное обозначение – Р. Рассмотрим, что такое периметр, основные способы его расчета для треугольных фигур разных видов.
Классическая формула
Самым простым способом найти периметр фигуры, если есть данные всех сторон. В этом случае используется следующая формула:
Буквой «P» обозначается сама величина периметра. В свою очередь «a», «b» и «c» – это длины сторон.

Зная размер трех величин, достаточно будет получить их сумму, которая и является периметром.
Это интересно! Что значит вертикально и как выглядит вертикальная линия
Альтернативный вариант
В математических задачах все данные длины редко бывают известны. В таких случаях рекомендуется воспользоваться альтернативным способом поиска нужной величины. Когда в условиях указана длина двух прямых, а также угол, находящийся между ними, расчет производится через поиск третьей. Для поиска этого числа необходимо добыть квадратный корень по формуле:
 .
.
Далее рассчитывайте Р по такой формуле:
 .
.
Периметр по двум сторонам
Для расчета периметра не обязательно знать все данные геометрической фигуры. Рассмотрим способы расчета по двум сторонам.
Равнобедренный треугольник
Равнобедренным называется такой треугольник, не меньше двух сторон которого имеют одинаковую длину. Они называются боковыми, а третья сторона – основанием. Равные прямые образовывают вершинный угол. Особенностью в равнобедренном треугольнике является наличие одной оси симметрии. Ось – вертикальная линия, выходящая из вершинного угла и заканчивающаяся посредине основания. По своей сути ось симметрии включает в себя такие понятия:
- биссектриса вершинного угла;
- медиана к основанию;
- высота треугольника;
- срединный перпендикуляр.
Чтобы определить периметр равнобедренного вида треугольной фигуры, воспользуйтесь формулой.
В данном случае вам необходимо знать только две величины: основание и длину одной стороны. Обозначение «2а» подразумевает умножение длины боковой стороны на 2. К полученной цифре нужно добавить величину основания – «b».
В исключительном случае, когда длина основания равнобедренного треугольника равна его боковой прямой, можно воспользоваться более простым способом. Он выражается в следующей формуле:
Для получения результата достаточно умножить это число на три. Эта формула используется для того, чтобы найти периметр правильного треугольника.
Это интересно! Изучаем символы: как обозначается в математике площадь
Полезное видео: задачи на периметр труегольника
Треугольник прямоугольный
Главным отличием прямоугольного треугольника от других геометрических фигур этой категории является наличие угла 90°. По этому признаку и определяется вид фигуры. Прежде, чем определить, как найти периметр прямоугольного треугольника, стоит заметить, что данная величина для любой плоской геометрической фигуры составляет сумму всех сторон. Так и в этом случае самый простой способ узнать результат – суммировать три величины.
В научной терминологии те стороны, которые прилегают к прямому углу, имеют название «катеты», а противоположная к углу 90º – гипотенуза. Особенности этой фигуры исследовались еще древнегреческим ученым Пифагором. Согласно с теоремой Пифагора, квадрат гипотенузы равен сумме квадратов катетов.
 .
.
На основании данной теоремы выведена еще одна формула, объясняющая, как найти периметр треугольника по двум известным сторонам. Рассчитать периметр при указанной длине катетов можно, используя следующий способ.
 .
.
Чтобы узнать периметр, имея информацию о размере одного катета и гипотенузы, нужно определить длину второй гипотенузы. С этой целью используют такие формулы:
 .
.
Также периметр описанного вида фигуры определяется и без данных о размерах катетов.
 .
.
Вам потребуется знать длину гипотенузы, а также угол, прилегающий к ней. Зная длину одного из катетов, если имеется угол, прилегающий к нему, периметр фигуры рассчитывают по формуле:
 .
.
Это интересно! Как найти и чему будет равна длина окружности
Расчет через высоту
Рассчитать периметр таких категорий, как равнобедренные и прямоугольные треугольники, можно через показатель их средней линии. Как известно, высота треугольника разделяет его основание пополам. Таким образом, она образует две прямоугольных фигуры. Далее, нужный показатель вычисляется при помощи теоремы Пифагора. Формула будет иметь следующий вид:
 .
.
Если известна высота и половина основания, используя этот способ, вы получите нужное число без поиска остальных данных о фигуре.
[spoiler title=”источники:”]
http://poschitat.online/perimetr-treugolnika
http://znaniya.guru/matematika/perimetr-treugolnika.html
[/spoiler]

Как найти периметр равностороннего треугольника
Поиск периметра равностороннего треугольника означает расчет расстояния вокруг самой фигуры. Самый простой способ – это сложить все стороны. Однако бывают случаи, когда известна лишь высота треугольника или одна сторона, как быть в таких ситуациях? Статья подскажет, как быстро находить периметр треугольника при разных условиях.
1
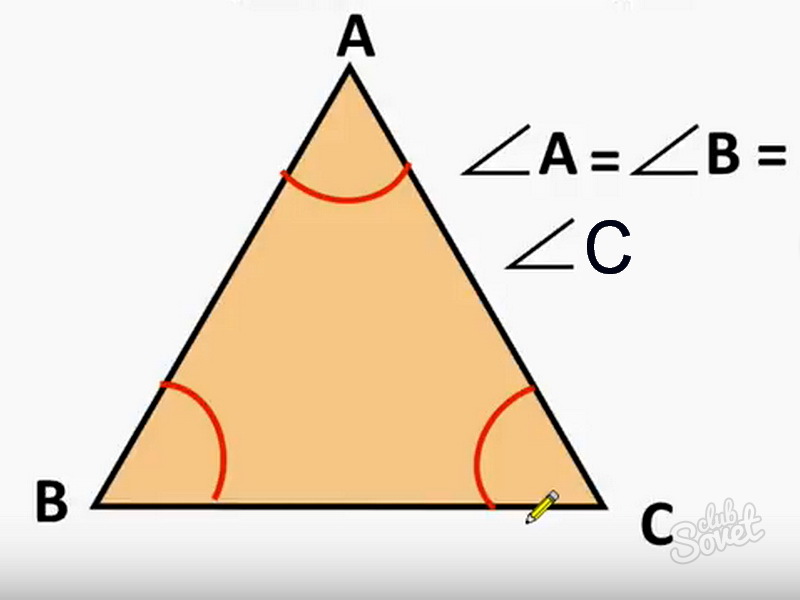
Равносторонний треугольник – что собой представляет
Такой треугольник имеет три конгруэнтные стороны и три равных угла. Зная размер одной из сторон, можно найти остальные. Поскольку треугольник имеет три соразмерные стороны, он автоматически имеет три идентичных угла. Они в сумме дают 180º, которую, согласно их идентичности, следует разделить на 3. Это означает, что любой угол треугольника равен 60 º. Можно сделать заключение, что равносторонний треугольник является острой фигурой.
2
Как найти периметр равностороннего треугольника
Поскольку стороны равностороннего треугольника конгруэнтны, для вычисления его периметра требуется длина одной стороны. Можно сказать, что простая формула периметра равносторонней фигуры : Р = c+c+c, где с – длина одной из сторон.
- Узнайте периметр треугольника с конгруэнтными сторонами, если размер одной – 7 дм.
- Из условия известно, что сторона фигуры 7 дм, т.е. другие стороны идентичны.
- Согласно формулы периметр треугольника: Р = с + с + с, Р = 7+7+7 = 21 дм.
3
Упрощенный способ нахождения периметра равностороннего треугольника
Конечно, более простой способ найти границы треугольника – это умножить длину каждой стороны на три. Формула будет состоять: P = 3 х а, где а – длина стороны.
- Оцените периметр равностороннего треугольника с заданной стороной 7 дм.
- Подставьте значения согласно формулы: P = 3 х а , P = 3 х 7
P = 21 - Периметр треугольника составляет 21 дм.
- Когда изначально стороны треугольника заданы в сантиметрах, ваш ответ также должен быть в сантиметрах. В приведенном примере длина сторон составляет 7 дм, поэтому правильное значение периметра будет 21 дм.
4
Как найти периметр равностороннего треугольника через высоту
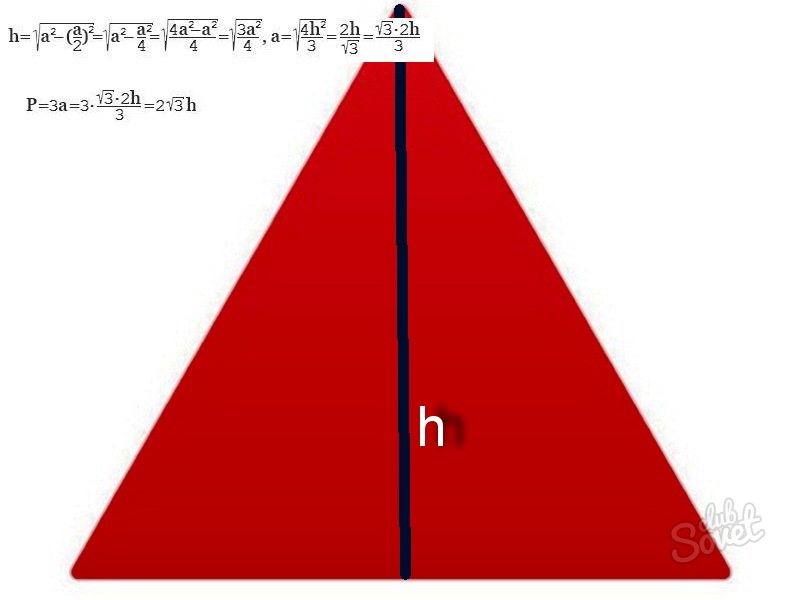
Рассчитать периметр равностороннего треугольника возможно, если дана одна высота. Следуя теореме Пифагора, найдите одну из сторон через высоту.
- Высота треугольника с равными сторонами 7 см, найдите периметр.
- Согласно условия h = 7 см, следуя формуле:
- Р= 2√3 х 7 = 24,249 см.
5
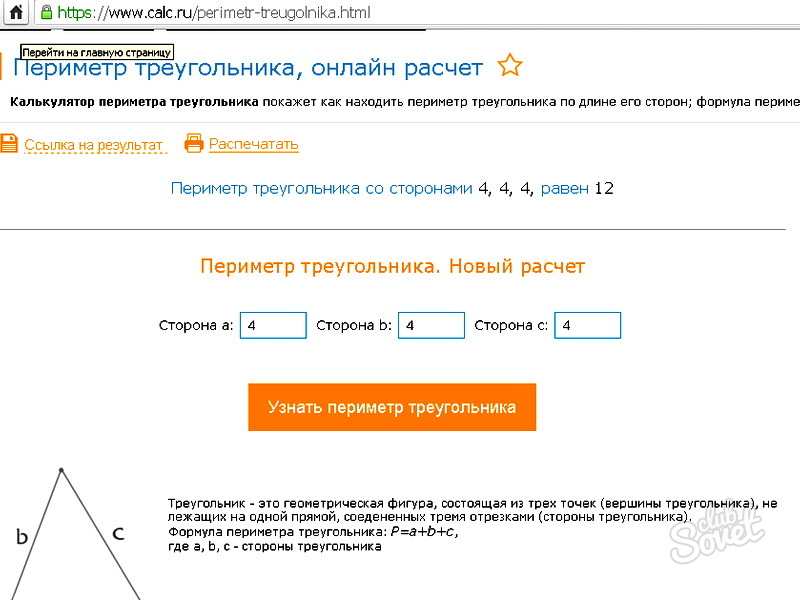
Онлайн расчет периметра равностороннего треугольника
Существует несколько сайтов (например, справочный портал Калькулятор или познавательный портал 2mb), которые помогут быстро рассчитать периметр треугольника, достаточно лишь ввести его параметры.
6
Как найти периметр равностороннего треугольника – обратный расчет
Бывают случаи, когда в школе требуется найти сторону равностороннего треугольника, когда в условии указан периметр фигуры. Примените полученные знания : Р = 3 х с, значит с = Р : 3
- Найдите длину стороны равностороннего треугольника, когда периметр 24 см.
- Исходя из формулы: с = Р : 3, с = 24 : 3 = 8 см
- Длина сторон заданного треугольника 8 см.

Нахождение периметра равностороннего треугольника не составит труда, если правильно применять основные формулы расчета.
Выбирайте формулу в зависимости от известных величин.
1. Как найти периметр треугольника, зная три стороны
Просто посчитайте сумму всех сторон.
- P — искомый периметр;
- a, b, c — стороны треугольника.
2. Как найти периметр треугольника, зная его площадь и радиус вписанной окружности
Умножьте площадь треугольника на 2.
Разделите результат на радиус вписанной окружности.
- P — искомый периметр;
- S — площадь треугольника;
- r — радиус вписанной окружности.
3. Как вычислить периметр треугольника, зная две стороны и угол между ними
Сначала найдите неизвестную сторону треугольника с помощью теоремы косинусов:
- Умножьте одну сторону на вторую, на косинус угла между ними и на 2.
- Посчитайте сумму квадратов известных сторон и отнимите от неё число, полученное в предыдущем действии.
- Найдите корень из результата.
Теперь прибавьте к найденной стороне две ранее известные стороны.
- P — искомый периметр;
- b, c — известные стороны треугольника;
- ɑ — угол между известными сторонами;
- a — неизвестная сторона треугольника.
4. Как найти периметр равностороннего треугольника, зная одну сторону
Умножьте сторону на 3.
- P — искомый периметр;
- a — любая сторона треугольника (напомним, в равностороннем треугольнике все стороны равны).
5. Как вычислить периметр равнобедренного треугольника, зная боковую сторону и основание
Умножьте боковую сторону на 2.
Прибавьте к результату основание.
- P — искомый периметр;
- a — боковая сторона треугольника (в равнобедренном треугольнике боковые стороны равны);
- b — основание треугольника (это сторона, которая отличается длиной от остальных).
6. Как найти периметр равнобедренного треугольника, зная боковую сторону и высоту
Найдите квадраты боковой стороны и высоты.
Отнимите от первого числа второе.
Найдите корень из результата и умножьте его на 2.
Прибавьте к полученному числу две боковые стороны.
- P — искомый периметр;
- a — боковая сторона треугольника;
- h — высота (перпендикуляр, опущенный на основание треугольника со стороны противоположной вершины; в равнобедренном треугольнике высота делит основание пополам).
7. Как вычислить периметр прямоугольного треугольника, зная катеты
Найдите квадраты катетов и посчитайте их сумму.
Извлеките корень из полученного числа.
Прибавьте к результату оба катета.
- P — искомый периметр;
- a, b — катеты треугольника (стороны, которые образуют прямой угол).
8. Как найти периметр прямоугольного треугольника, зная катет и гипотенузу
Посчитайте квадраты гипотенузы и катета.
Отнимите от первого числа второе.
Найдите корень из результата.
Прибавьте катет и гипотенузу.
- P — искомый периметр;
- a — любой катет прямоугольника;
- c — гипотенуза (сторона, которая лежит напротив прямого угла).
Периметр равностороннего треугольника


4.4
Средняя оценка: 4.4
Всего получено оценок: 324.
4.4
Средняя оценка: 4.4
Всего получено оценок: 324.
Равносторонний треугольник занимает особое место среди треугольников. Для того, чтобы найти значение периметра, площади, углов или радиусов окружностей вписанной и описанной у равнобедренного треугольника, достаточно знать величину стороны. С одной стороны, это значительно облегчает решение, с другой составители задач редко дают значение стороны и приходится искать обходные пути решения.
Формула нахождения периметра равностороннего треугольника
Формула периметра равностороннего треугольника вытекает из определений. Что такое периметр? Периметр это сумма всех сторон фигуры. Равносторонний треугольник – это треугольник, все стороны которого равны.
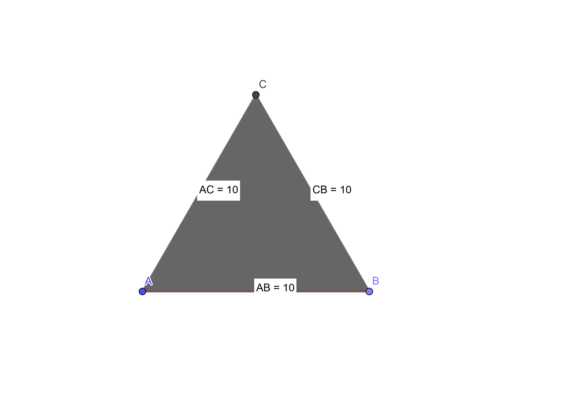
Значит,для того, чтобы найти значение периметра достаточно умножить величину стороны на количество сторон:
P=3*a
Решим несколько разных по сложности задач, чтобы разобраться, какие проблемы могут встречаться на пути нахождения периметра.
Задача 1
- В равностороннем треугольнике сторона равна 6. Найти периметр треугольника.
Это самый простой вариант задачи. Достаточно подставить значение в формулу и получить результат. Такая задача не должна вызывать затруднений:
P=3*a=3*6=18
Задача 2
- В равнобедренном треугольнике острый угол при основании равен 60 градусам, площадь треугольника равна $${64oversqrt{3}}$$.
Особое внимание нужно обращать на вид фигуры, который указан в условии задачи.
В данной задаче дан равнобедренный треугольник. Чтобы воспользоваться общей формулой, необходимо доказать, что этот равнобедренный треугольник является еще и равносторонним.
Обратим внимание на величину угла. Угол при основании равен 60. При этом углы у основания равнобедренного треугольника равны, а сумма углов любого треугольника равна 180 градусов. Значит у основания два угла по 60 градусов. Рассчитаем угол при вершине:
180-60-60=60 – угол при вершине так же равен 60 градусам.
Значит, данный треугольник будет равносторонним, так как все углы равны 60 градусам.
Углы по 60 градусов характерны только для равностороннего треугольника. Именно сочетание 3 равных сторон образует 3 равных угла. В любых других ситуациях, хотя бы один угол будет отличаться.
Для площади равностороннего треугольника имеется отдельная формула:
$$S=a^2*{sqrt{3}over 4}={64oversqrt{3}}$$ – где а значение стороны, которое нам и нужно выразить из этой формулы.
$$а^2={Sover{sqrt{3}over 4}}$$
$$a^2={4Soversqrt{3}}$$
$$a=sqrt{4Soversqrt{3}}$$
$$a={sqrt{4*{64oversqrt{3}^2}}oversqrt{3}}=sqrt{4*64}=16$$
Подставим полученное значение в формулу:
P=3*a=3*16=48
Задача 3
- В равностороннем треугольнике высота равна $$3*sqrt{3}$$. Найти периметр треугольника.
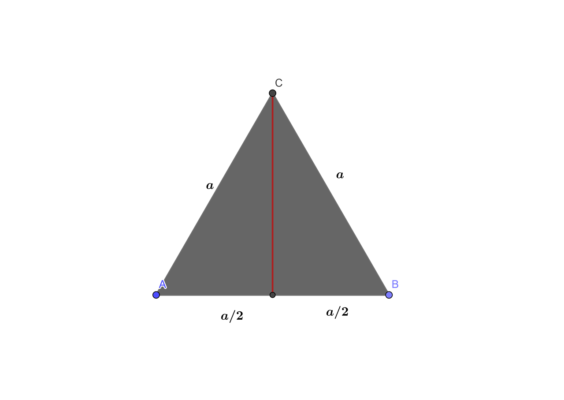
Для данной задачи нужно воспользоваться методом решения, который часто используется в задачах с равнобедренным треугольником. Из любой вершины опустим высоту, которая будет медианой и биссектрисой.
В одном из получившихся треугольников выразим значение высоты через сторону с помощью теоремы Пифагора:
$$h^2=a^2-({aover2})^2$$
$$h^2=a^2-{a^2over4}$$
Вычтем подобные слагаемые:
$$h^2={3over4}*a^2$$
Из получившейся формулы выразим значение стороны:
$$a^2={4over3}*h^2$$
$$a=sqrt{{4over3}*h^2}$$
$$a=sqrt{{4over3}*(3*sqrt{3})^2}$$
$$a=sqrt{{4over3}*(9*3)}$$
$$a=sqrt{4*9}$$
a=6
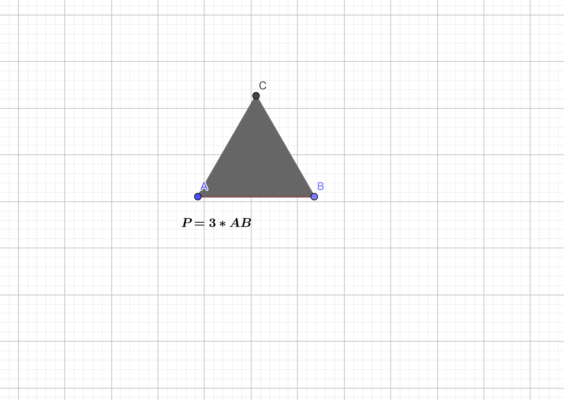
Подставим получившееся значение в формулу периметра равностороннего треугольника.
P=3*a=3*6=18

Что мы узнали?
Мы обсудили формулу для нахождения периметра равностороннего треугольника. Выделили проблемы, которые приходится решать при нахождении стороны равностороннего треугольника для дальнейшего решения задачи. Рассмотрели различные пути решения задач на нахождение периметра равностороннего треугольника.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-

Марго Дудченко
4/5
-

Татьяна Коробейникова
5/5
-

Наташа Новак
4/5
-

Марина Безобразова
4/5
-

Даниил Толыпин
5/5
-

Ибрагим Вафя-Сулим
5/5
-

Наталия Левина
4/5
-

Исмаил Тагиев
5/5
Оценка статьи
4.4
Средняя оценка: 4.4
Всего получено оценок: 324.
А какая ваша оценка?
