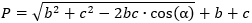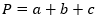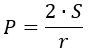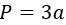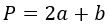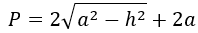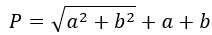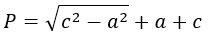Выбирайте формулу в зависимости от известных величин.
1. Как найти периметр треугольника, зная три стороны
Просто посчитайте сумму всех сторон.
- P — искомый периметр;
- a, b, c — стороны треугольника.
2. Как найти периметр треугольника, зная его площадь и радиус вписанной окружности
Умножьте площадь треугольника на 2.
Разделите результат на радиус вписанной окружности.
- P — искомый периметр;
- S — площадь треугольника;
- r — радиус вписанной окружности.
3. Как вычислить периметр треугольника, зная две стороны и угол между ними
Сначала найдите неизвестную сторону треугольника с помощью теоремы косинусов:
- Умножьте одну сторону на вторую, на косинус угла между ними и на 2.
- Посчитайте сумму квадратов известных сторон и отнимите от неё число, полученное в предыдущем действии.
- Найдите корень из результата.
Теперь прибавьте к найденной стороне две ранее известные стороны.
- P — искомый периметр;
- b, c — известные стороны треугольника;
- ɑ — угол между известными сторонами;
- a — неизвестная сторона треугольника.
4. Как найти периметр равностороннего треугольника, зная одну сторону
Умножьте сторону на 3.
- P — искомый периметр;
- a — любая сторона треугольника (напомним, в равностороннем треугольнике все стороны равны).
5. Как вычислить периметр равнобедренного треугольника, зная боковую сторону и основание
Умножьте боковую сторону на 2.
Прибавьте к результату основание.
- P — искомый периметр;
- a — боковая сторона треугольника (в равнобедренном треугольнике боковые стороны равны);
- b — основание треугольника (это сторона, которая отличается длиной от остальных).
6. Как найти периметр равнобедренного треугольника, зная боковую сторону и высоту
Найдите квадраты боковой стороны и высоты.
Отнимите от первого числа второе.
Найдите корень из результата и умножьте его на 2.
Прибавьте к полученному числу две боковые стороны.
- P — искомый периметр;
- a — боковая сторона треугольника;
- h — высота (перпендикуляр, опущенный на основание треугольника со стороны противоположной вершины; в равнобедренном треугольнике высота делит основание пополам).
7. Как вычислить периметр прямоугольного треугольника, зная катеты
Найдите квадраты катетов и посчитайте их сумму.
Извлеките корень из полученного числа.
Прибавьте к результату оба катета.
- P — искомый периметр;
- a, b — катеты треугольника (стороны, которые образуют прямой угол).
8. Как найти периметр прямоугольного треугольника, зная катет и гипотенузу
Посчитайте квадраты гипотенузы и катета.
Отнимите от первого числа второе.
Найдите корень из результата.
Прибавьте катет и гипотенузу.
- P — искомый периметр;
- a — любой катет прямоугольника;
- c — гипотенуза (сторона, которая лежит напротив прямого угла).
Периметр треугольника калькулятор онлайн умеет вычислять периметр восемью способами:
- По трем сторонам.
- По площади и радиусу вписанной окружности.
- По двум сторонам и углу между ними.
- По стороне равностороннего треугольника.
- По боковой стороне и основанию равнобедренного треугольника.
- По боковой стороне и высоте равнобедренного треугольника.
- По катетам прямоугольного треугольника.
- По одному катету и гипотенузе прямоугольного треугольника.
Сделав расчет периметра на этом онлайн калькуляторе Вы получите не только ответ, но и детальное, пошаговое решение с выводом формул и промежуточных действий.
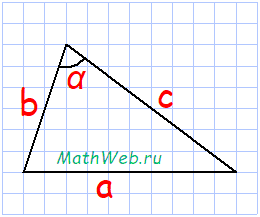
Треугольник – это геометрическая фигура, состоящая из трех точек (вершины треугольника), не лежащих на одной прямой, соедененных тремя отрезками (стороны треугольника).
Формула периметра треугольника: 
где b,c – стороны треугольника, α° – угол между ними.
Решение:
P = √b2 + с2 – 2bc·cos(α°) + b + c
= √12 + 22 – 2·1·2·cos(40°) + 1 + 2
= √1 + 4 – 3.064 + 3
= √1.936 + 3
= 1.391 + 3
=
4.391
Ответ: Периметр треугольника со сторонами b = 1, c = 2 и углом между ними α° = 40 равен 4.391
Периметр треугольника- это сумма трех сторон.
Периметр может быть найден и по другим формулам, вывод которых основан на поиске длины неизвестной стороны.
Как найти периметр треугольника?
Найти периметр треугольника очень просто на нашем онлайн калькуляторе. Так же периметр может быть найден самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.
1) По трем сторонам
где a,b,c – стороны треугольника.
2) По площади и радиусу вписанной окружности
где S – площадь треугольника, r – радиус вписанной окружности.
3) По двум сторонам и углу между ними
где b,c – стороны треугольника, α° – угол между ними.
4) По стороне равностороннего треугольника
где a – сторона равностороннего треугольника.
5) По боковой стороне и основанию равнобедренного треугольника
где a – боковая сторона и b – основание равнобедренного треугольника.
6) По боковой стороне и высоте равнобедренного треугольника
где a – боковая сторона и h – высота равнобедренного треугольника.
7) По катетам прямоугольного треугольника
где a,b – катеты прямоугольного треугольника.
8) По одному катету и гипотенузе прямоугольного треугольника.
где а – катет и с – гипотенуза прямоугольного треугольника.
Скачать все формулы в формате Word
Download Article
Download Article
Finding the perimeter of a triangle means finding the distance around the triangle.[1]
The simplest way to find the perimeter of a triangle is to add up the length of all of its sides, but if you don’t know all of the side lengths you will need to calculate them first. This article will first teach you to find the perimeter of a triangle when you do know all three side lengths; this is the easiest and most common way. It will then teach you to find the perimeter of a right triangle when only two of the side lengths are known. Finally, it will teach you to find the perimeter of any triangle for which you know two side lengths and the angle measure between them (an “SAS Triangle”), using the Law of Cosines.
-
1
Remember the formula for finding the perimeter of a triangle. For a triangle with sides a, b and c, the perimeter P is defined as: P = a + b + c.[2]
- What this formula means in simpler terms is that to find the perimeter of a triangle, you just add together the lengths of each of its 3 sides.
-
2
Look at your triangle and determine the lengths of the three sides. In this example, the length of side a = 5, the length of side b = 5, and the length of side c = 5.
- This particular example is called an equilateral triangle, because all three sides are of equal length. But remember that the perimeter formula is the same for any kind of triangle.
Advertisement
-
3
Add the three side lengths together to find the perimeter. In this example, 5 + 5 + 5 = 15. Therefore, P = 15.
- In another example, where a = 4, b = 3, and c=5, the perimeter would be: P = 3 + 4 + 5, or 12.
-
4
Remember to include the units in your final answer. If the sides of the triangle are measured in centimeters, then your answer should also be in centimeters. If the sides are measured in terms of a variable like x, your answer should also be in terms of x.[3]
- In this example, the side lengths are each 5cm, so the correct value for the perimeter is 15cm.
Advertisement
-
1
Remember what a right triangle is. A right triangle is a triangle that has one right (90 degree) angle. The side of the triangle opposite the right angle is always the longest side, and it is called the hypotenuse. Right triangles show up frequently on math tests, and fortunately there is a very handy formula for finding the length of unknown sides!
-
2
Recall the Pythagorean Theorem. The Pythagorean Theorem tells us that for any right triangle with sides of length a and b, and hypotenuse of length c, a2 + b2 = c2.[4]
-
3
Look at your triangle, and label the sides “a,” “b,” and “c”. Remember that the longest side of the triangle is called the hypotenuse. It will be opposite the right angle and must be labeled c. Label the two shorter sides a and b. It doesn’t really matter which is which, the math will turn out the same!
-
4
Enter the side lengths that you know into the Pythagorean Theorem. Remember that a2 + b2 = c2. Substitute the side lengths in for the corresponding letters in the equation.[5]
- If, for example, you know that side a = 3 and side b = 4, then plug those values into the formula as follows: 32 + 42 = c2.
- If you know the length of side a = 6, and the hypotenuse c = 10, then you should set the equation up like so: 62 + b2 = 102.
-
5
Solve the equation to find the missing side length. You will first need to square the known side lengths which means multiplying each value by itself (for example 32 = 3 * 3 = 9). If you are looking for the hypotenuse, simply add the two values together and find the square root of this number to find the length. If it is a side length you are missing, you must do a bit of easy subtraction, and then take the square root to get your side length.[6]
- In the first example, square the values in 32 + 42 = c2 and find that 25= c2. Then calculate the square root of 25 to find that c = 5.
- In the second example, square the values in 62 + b2 = 102 to find that 36 + b2 = 100. Subtract 36 from each side to find that b2 = 64, then take the square root of 64 to find that b = 8.
-
6
Add up the lengths of the three side lengths to find the perimeter. Recall that the perimeter P = a + b + c. Now that you know the lengths of sides a, b and c, you simply need to add the lengths together to find the perimeter.[7]
- In our first example,P = 3 + 4 + 5, or 12.
- In our second example, P = 6 + 8 + 10, or 24.
Do you have the perimeter and are missing one side? Then you should subtract the sum of the two sides from the perimeter. This number equals the length of the missing side.
Advertisement
-
1
Learn the Law of Cosines. The Law of Cosines allows you to solve any triangle when you know two side lengths and measurement of the angle between them. It works on any triangle, and is a very useful formula. The Law of Cosines states that for any triangle with sides a, b, and c, with opposite angles A, B, and C: c2 = a2 + b2 – 2ab cos(C).[8]
[9]
-
2
Look at your triangle and assign variable letters to its components. The first side that you know should be labeled a, and the angle opposite it is A. The second side that you know should be labeled b; the angle opposite it is B. The angle that you know should be labeled C, and the third side, the one you need to solve in order to find the perimeter of the triangle, is side c.[10]
- For example, imagine a triangle with side lengths 10 and 12, and an angle between them of 97°. We will assign variables as follows: a = 10, b = 12, C = 97°.
-
3
Plug your information into the equation and solve for side c. You will first need to find the squares of a and b, and add them together. Then find the cosine of C using the cos function on your calculator, or an online cosine calculator.[11]
Multiply cos(C) by 2ab and subtract the product from the sum of a2 + b2. The result is c2. Find the square root of this value and you have the length of side c.[12]
Using our example triangle:- c2 = 102 + 122 – 2 × 10 × 12 × cos(97).
- c2 = 100 + 144 – (240 × -0.12187) (Round the cosine to 5 decimal places.)
- c2 = 244 – (-29.25)
- c2 = 244 + 29.25 (Carry the minus symbol through when cos(C) is negative!)
- c2 = 273.25
- c = 16.53
-
4
Use side length c to find the perimeter of the triangle. Recall that Perimeter P = a + b + c, so all you need to do is add the length you just calculated for side c to the values you already had for a and b.
- In our example: 10 + 12 + 16.53 = 38.53, the perimeter of our triangle!
Advertisement
Triangle Perimeter Calculator, Practice Problems, and Answers
Add New Question
-
Question
Can you find the perimeter if only one side is given?
This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.
wikiHow Staff Editor
Staff Answer
If you know only 1 side but all 3 angles, you can use the rule of sines to find the remaining sides, then calculate the perimeter. If you know 1 side and 1 angle, you won’t be able to find the perimeter unless you’re dealing with a right triangle. For right triangles, you know that 1 angle is always 90°, so if you know another angle, you can use the sum of angles (180°) to figure out the third one. From there, you can use the laws of sine and cosine to figure out the other sides.
-
Question
How can you find the perimeter of a triangle if one side is missing?
This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.
wikiHow Staff Editor
Staff Answer
If it’s a right triangle, you can use the Pythagorean theorem (a2 + b2 = c2) to find the length of the missing side. From there, you can easily calculate the perimeter. For other types of triangles, you can use the law of cosines to find the perimeter if you know 2 sides and at least 1 of the angles.
-
Question
How can you find the missing side of a triangle given the perimeter?
This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.
wikiHow Staff Editor
Staff Answer
Since the perimeter is the sum of the lengths of all sides, you can solve for the missing side by subtracting the lengths of the other 2 sides from the perimeter.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
References
About This Article
Article SummaryX
To find the perimeter of a triangle, use the formula perimeter = a + b + c, where a, b, and c are the lengths of the sides of the triangle. For example, if the length of each side of the triangle is 5, you would just add 5 + 5 + 5 and get 15. Therefore, the perimeter of the triangle is 15. If you only know the length of 2 of the triangle’s sides, you can still find the perimeter if it’s a right triangle, which means the triangle has one 90-degree angle. Just use the Pythagorean theorem, which is a^2+ b^2 = c^2, where a and b are the lengths of the known sides and c is the length of the unknown hypotenuse. For example, if the length of the known sides are 3 and 4, you would just add 3^2+ 4^2, or 9 + 16, and get 25. Then, you would take the square root of 25 to find c, which is 5. Therefore, the length of the unknown side is 5. Finally, add all of the side lengths together to find the perimeter. In this case you would add 3 + 4 + 5 and get 12. Therefore, the perimeter of the triangle is 12. If you want to learn how to solve the perimeter of your triangle if you only know 2 sides and an angle, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 1,729,411 times.
Reader Success Stories
-
“This was really helpful for me. It was easy to understand, and it gives a lot of information. I really appreciated…” more
Did this article help you?
Формулы периметра треугольника
Как найти периметр любого треугольника? Существует
множество способов сделать это, но мы расскажем про
основные. В этой статье вы узнаете, как найти периметр
любого треугольника через известные величины, по формулам.
Ⅰ. Через площадь и радиус вписанной окружности
Известно: площадь и радиус вписанной окружности треугольника.
Чтобы найти периметр любого треугольника,
нужно две площади треугольника разделить
на радиус вписанной окружности.
Как видим, для этой формулы нужно знать всего
лишь радиус вписанной окружности и площадь.
Ⅱ. Через три стороны
Известно: три стороны треугольника.
Чтобы найти периметр любого треугольника,
нужно сложить все стороны треугольника.
Результатом и будет периметр.
Это самая простая формула.
Ⅲ. Через Теорему Косинусов
Известно: две стороны и угол между ними.
Чтобы найти периметр любого треугольника,
нужно для начала найти третью сторону треугольника,
затем косинус угла, если косинус неизвестен.
Это формулу удобней применить,
если вам известны две стороны
и косинус между ними.
Нахождение периметра треугольника: формула и задачи
В данной публикации мы рассмотрим, каким образом можно посчитать периметр треугольника и разберем примеры решения задач.
Формула вычисления периметра
Периметр (P) любого треугольника равняется сумме длин всех его сторон.
P = a + b + c
Периметр равнобедренного треугольника
Равнобедренным называют треугольник, у которого две боковые стороны равны (примем их за b). Сторона a, имеющая отличную от боковых длину, является основанием. Таким образом, периметр можно считать так:
P = a + 2b
Периметр равностороннего треугольника
Равносторонним или правильным называется треугольник, у которого все стороны равны (примем ее за a). Периметр такой фигуры вычисляется так:
P = 3a
Примеры задач
Задание 1
Найдите периметр треугольника, если его стороны равны: 3, 4 и 5 см.
Решение:
Подставляем в формулу известные по условиям задачи величины и получаем:
P = 3 см + 4 см + 5 см = 12 см.
Задание 2
Найдите периметр равнобедренного треугольника, если его основание равняется 10 см, а боковая сторона- 8 см.
Решение:
Как мы знаем, боковые стороны равнобедренного треугольника равны, следовательно:
P = 10 см + 2 ⋅ 8 см = 26 см.
Как найти периметр треугольника
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение
Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской буквой P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах и ходе решении.
Важно, чтобы все параметры были переданы в одной единице длины, иначе мы не сможем подсчитать результат. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
В чем измеряется периметр:
Как узнать периметр треугольника
Рассмотрим какие существуют формулы, и при каких известных исходных данных их можно применять.
Если известны три стороны, то периметр треугольника равен их сумме. Этот способ проходят во втором классе.
P = a + b + c, где a, b, c — длина стороны.
Если известна площадь и радиус вписанной окружности:
P = 2 * S : r, где S — площадь, r — радиус вписанной окружности.
Если известны две стороны и угол между ними, вычислить периметр треугольника можно так:
P = √ b 2 + с 2 – 2 * b * с * cosα + (b + с), где b, с — известные стороны, α — угол между известными сторонами.
Если известна одна сторона в равностороннем треугольнике:
P = 3 * a, где a — длина стороны.
Все стороны в равносторонней фигуре равны.
Если известна боковая сторона и основание в равнобедренном треугольнике:
P = 2 * a + b, где a — боковая сторона, b — основание.
Боковые стороны в равнобедренной фигуре равны.
Если известна боковая сторона и высота в равнобедренном треугольнике:
P = 2 * (√ a 2 + h 2 ) + 2 * a, где a — боковая сторона, h — высота.
Высотой принято называть отрезок, который вышел из вершины и опустился на основание. В равнобедренной фигуре высота делит основание пополам.
Если известны катеты в прямоугольном треугольнике:
P = √ a 2 + b 2 + (a + b), где a, b — катеты.
Катет — одна из двух сторон, которые образуют прямой угол.
Если известны катет и гипотенуза в прямоугольном треугольнике:
P = √ c 2 – a 2 + (a + c), где a — любой катет, c — гипотенуза.
Гипотенуза — сторона, которая лежит напротив прямого угла.
Скачать онлайн таблицу
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/perimetr-treugolnika
[/spoiler]
Периметр — это величина, подразумевающая длину всех сторон плоской (двумерной) геометрической фигуры. Для разных геометрических фигур существуют разные способы нахождения периметра.
В данной статье вы узнаете как находить периметр фигуры разными способами, в зависимости от известных его граней.
…
Оглавление:
- Первый метод: известны все стороны фигуры
- Второй метод: прямоугольный треугольник и две известные его стороны
- Третий метод: по двум граням и углу между ними
Возможные методы:
- известны все три стороны равнобедренного или любого другого треугольника;
- как найти периметр прямоугольного треугольника при двух известных его гранях;
- известны две грани и угол, который расположен между ними (формула косинусов) без средней линии и высоты.
Это интересно: что микроэкономика изучает, кратко об основателях и основах науки.
Первый метод: известны все стороны фигуры
Как находить периметра треугольника, когда известны все три грани, необходимо использовать следующую формулу: P = a + b + c, где a,b,c — известные длины всех сторон треугольника, P — периметр фигуры.
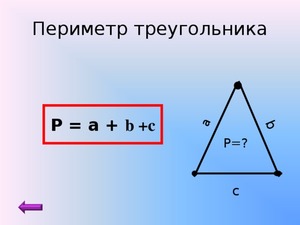
Например, известны три стороны фигуры: a = 24 см, b = 24 см, c = 24 см. Это правильная равнобедренная фигура, чтобы вычислить периметр пользуемся формулой: P = 24 + 24 + 24 = 72 см.
Данная формула подходит к любому треугольнику, необходимо просто знать длины всех его сторон. Если хотя бы одна из них неизвестна, необходимо воспользоваться другими способами, о которых мы поговорим ниже.
Еще один пример: a = 15 см, б = 13 см, c = 17 см. Вычисляем периметр: P = 15 + 13 + 17 = 45 см.
Очень важно помечать единицу измерения в полученном ответе. В наших примерах длины сторон указаны в сантиметрах (см), однако, существуют разные задачи, в условиях которых присутствуют другие единицы измерения.
Это интересно: что понимают под образовательными информационными ресурсами?
Второй метод: прямоугольный треугольник и две известные его стороны
В том случае, когда в задании, которое нужно решить, дана прямоугольная фигура, длины двух граней которой известны, а третья нет, необходимо воспользоваться теоремой Пифагора.
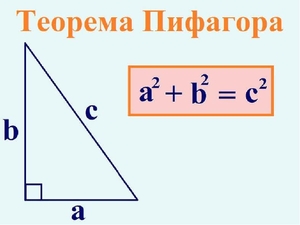
Теорема Пифагора описывает соотношение между гранями прямоугольного треугольника. Формула, описываемая этой теоремой, является одной из самых известных и наиболее часто применяемых теорем в геометрии. Итак, сама теорема:
Стороны любого прямоугольного треугольника описываются таким уравнением: a^2 + b^2 = c^2, где а и b — катеты фигуры, а c — гипотенуза.
- Гипотенуза. Она всегда расположена противоположно прямому углу (90 градусов), а также является самой длинной гранью треугольника. В математике принято обозначать гипотенузу буквой c.
- Катеты — это грани прямоугольного треугольника, которые относятся к прямому углу и обозначаются буквами а и b. Один из катетов одновременно является и высотой фигуры.
Таким образом, если условиями задачи заданы длины двух из трех граней такой геометрической фигуры, с помощью теоремы Пифагора необходима найти размерность третьей грани, после чего воспользоваться формулой из первого метода.
Например, мы знаем длину 2-х катетов: a = 3 см, b = 5 см. Подставляем значения в теорему: 3^2 + 4^2 = c^2 => 9 + 16 = c^2 => 25 = c^2 => c = 5 см. Итак, гипотенуза такого треугольника равна 5 см. К слову, данный пример является самым распространенным и называется «Египетский треугольник». Иными словами, если два катета фигуры равны 3 см и 4 см, то гипотенуза составит 5 см соответственно.
Если неизвестна длина одного из катетов, необходимо преобразовать формулу следующим образом: c^2 — a^2 = b^2. И наоборот для другого катета.
Продолжим пример. Теперь необходимо обратиться к стандартной формуле поиска периметра фигуры: P = a + b + c. В нашем случае: P = 3 + 4 + 5 = 12 см.
Третий метод: по двум граням и углу между ними
В старшей школе, а также университете, чаще всего приходится обращаться именно к данному способу нахождения периметра. Если условиями задачи заданы длины двух сторон, а также размерность угла между ними, то необходимо воспользоваться теоремой косинусов.
Данная теорема применима абсолютно к любому треугольнику, что и делает ее одной из наиболее полезных в геометрии. Сама теорема выглядит следующим образом: c^2 = a^2 + b^2 — (2 * a * b * cos(C)), где a,b,c — стандартно длины граней, а A,B и С — это углы, которые лежат напротив соответствующих граней треугольника. То есть, A — угол, противолежащий стороне a и так далее.
Представим, что описан треугольник, стороны а и б которого составляют 100 см и 120 см соответственно, а угол, лежащий между ними, составляет 97 градусов. То есть а = 100 см, б = 120 см, C = 97 градусов.
Все, что нужно сделать в данном случае — это подставить все известные значения в теорему косинусов. Длины известных граней возводятся в квадрат, после чего известные стороны перемножаются между друг другом и на два и умножаются на косинус угла между ними. Далее, необходимо сложить квадраты граней и отнять от них второе полученное значение. Из итоговой величины извлекается квадратный корень — это будет третья, неизвестная до этого сторона.
После того как все три грани фигуры известны, осталось воспользоваться уже полюбившейся нам стандартной формулой поиска периметра описываемой фигуры из первого метода.
Задача решена.
