1) Измерь стороны многоугольников и найди периметр каждого из них в сантиметрах.
2) Вспомни, как, используя циркуль, находили длину ломаной. Расскажи, как можно найти периметр многоугольника, не узнавая длину каждой из его сторон. Найди этим способом периметр треугольника.
reshalka.com
ГДЗ учебник по математике 2 класс Моро. Часть 1. Страница 42. Номер №1
Решение 1
Первая фигура:
3 + 4 + 1 + 4 = 7 + 1 + 4 = 8 + 4 = 12 (см) − периметр первой фигуры.
Вторая фигура:
4 + 3 + 3 = 7 + 3 = 10 (см) − периметр второй фигуры.
Третья фигура:
2 + 3 + 5 + 5 = 5 + 5 + 5 = 10 + 5 = 15 (см) − периметр третьей фигуры.
Решение 2
Начертим прямую. С помощью циркуля отложим на прямой один за другим отрезки, равные по длине отрезкам фигуры 1, и узнаем длину всего получившегося отрезка (12 см).
Начертим прямую. С помощью циркуля отложим на прямой один за другим отрезки, равные по длине отрезкам фигуры 2, и узнаем длину всего получившегося отрезка (10 см).
Начертим прямую. С помощью циркуля отложим на прямой один за другим отрезки, равные по длине отрезкам фигуры 3, и узнаем длину всего получившегося отрезка (15 см).
Первый способ.
Я бы на месте этого потенциального второклассника взял обыкновенную нитку,
конец её прижал в одном из углов треугольника,
протянул нитку по одной из сторон
(удерживая при этом конец нитки в первой точке),
попросил соседа по парте прижать нитку во втором углу,
протянул нитку по второй стороне, опять попросил соседа
прижать нитку ещё и во втором углу треугольника, и,
наконец, дотянул нитку до последнего угла и обрезал её в точке первого угла.
Теперь осталось только приложить эту нитку к линейке и, вот он – периметр!
Второй способ.
Берём циркуль, иголкой ставим его в точку первого угла треугольника, второй конец циркуля дотягиваем до точки второго угла треугольника.
Отчёркиваем на листе прямую линию. Откладываем на ней первый “раствор” циркуля.
Затем таким же образом измеряем вторую сторону треугольника и откладываем циркулем эту длину как продолжение первого замера.
Измеряем циркулем третью сторону и опять откладываем её как продолжение линии.
Получается линия, состоящая из трёх последовательных отрезков, равная периметру треугольника. Измеряем её линейкой – получаем искомый периметр.
Выбирайте формулу в зависимости от известных величин.
1. Как найти периметр треугольника, зная три стороны
Просто посчитайте сумму всех сторон.
- P — искомый периметр;
- a, b, c — стороны треугольника.
2. Как найти периметр треугольника, зная его площадь и радиус вписанной окружности
Умножьте площадь треугольника на 2.
Разделите результат на радиус вписанной окружности.
- P — искомый периметр;
- S — площадь треугольника;
- r — радиус вписанной окружности.
3. Как вычислить периметр треугольника, зная две стороны и угол между ними
Сначала найдите неизвестную сторону треугольника с помощью теоремы косинусов:
- Умножьте одну сторону на вторую, на косинус угла между ними и на 2.
- Посчитайте сумму квадратов известных сторон и отнимите от неё число, полученное в предыдущем действии.
- Найдите корень из результата.
Теперь прибавьте к найденной стороне две ранее известные стороны.
- P — искомый периметр;
- b, c — известные стороны треугольника;
- ɑ — угол между известными сторонами;
- a — неизвестная сторона треугольника.
4. Как найти периметр равностороннего треугольника, зная одну сторону
Умножьте сторону на 3.
- P — искомый периметр;
- a — любая сторона треугольника (напомним, в равностороннем треугольнике все стороны равны).
5. Как вычислить периметр равнобедренного треугольника, зная боковую сторону и основание
Умножьте боковую сторону на 2.
Прибавьте к результату основание.
- P — искомый периметр;
- a — боковая сторона треугольника (в равнобедренном треугольнике боковые стороны равны);
- b — основание треугольника (это сторона, которая отличается длиной от остальных).
6. Как найти периметр равнобедренного треугольника, зная боковую сторону и высоту
Найдите квадраты боковой стороны и высоты.
Отнимите от первого числа второе.
Найдите корень из результата и умножьте его на 2.
Прибавьте к полученному числу две боковые стороны.
- P — искомый периметр;
- a — боковая сторона треугольника;
- h — высота (перпендикуляр, опущенный на основание треугольника со стороны противоположной вершины; в равнобедренном треугольнике высота делит основание пополам).
7. Как вычислить периметр прямоугольного треугольника, зная катеты
Найдите квадраты катетов и посчитайте их сумму.
Извлеките корень из полученного числа.
Прибавьте к результату оба катета.
- P — искомый периметр;
- a, b — катеты треугольника (стороны, которые образуют прямой угол).
8. Как найти периметр прямоугольного треугольника, зная катет и гипотенузу
Посчитайте квадраты гипотенузы и катета.
Отнимите от первого числа второе.
Найдите корень из результата.
Прибавьте катет и гипотенузу.
- P — искомый периметр;
- a — любой катет прямоугольника;
- c — гипотенуза (сторона, которая лежит напротив прямого угла).
Загрузить PDF
Загрузить PDF
Нахождение периметра фигуры – порой непростая задача. Эта статья научит вас находить периметры следующих основных фигур: прямоугольника, квадрата, круга, прямоугольного треугольника, треугольника и правильного многоугольника.
-
1
Найдите длины двух смежных сторон: ширины и высоты. Прямоугольник – фигура с четырьмя сторонами, которые пересекаются под прямым углом, а две противоположные стороны параллельны и равны. Таким образом, две смежные стороны имеют разную длину (ширина и высота; если ширина равна высоте, то такая фигура – квадрат).
- Если даны только одна сторона и площадь прямоугольника, вы можете найти другую сторону по формуле: A=wh, то есть h=A/w или w=A/h. Поэтому, если даны высота и площадь, просто разделите площадь на высоту, чтобы найти ширину. Вы также можете разделить площадь на ширину, чтобы найти высоту.
-
2
Сложите длины двух смежных сторон и умножьте полученное значение на 2. Если w – ширина и h – высота, периметр прямоугольника: P=2(w+h)
Реклама
-
1
Найдите длину стороны квадрата (назовем ее х). Квадрат – фигура, у которой все стороны равны и пресекаются под прямым углом.
-
2
Если дана площадь (A) квадрата, вы можете найти длину стороны, взяв квадратный корень из площади: х = √ (A).
- Если дана диагональ (d) квадрата, Вы можете найти длину стороны, разделив диагональ на квадратный корень из 2: х = d/√2
-
3
Умножьте длину стороны на четыре. Поскольку все четыре стороны имеют одинаковую длину, периметр квадрата равен учетверенной длине одной стороны: Р = 4x.
Реклама
-
1
Найдите длину радиуса (r). Радиус является расстоянием от центра круга до любой точки на окружности.
- Если дан диаметр (d) круга, вы можете найти радиус, разделив диаметр на два: г = d/2
- Если дана площадь (A) круга, вы можете найти радиус, разделив площадь на π, а затем взяв квадратный корень из полученного значения: г = √(A/π)
-
2
Найдите периметр, умножив радиус на 2π: Р = 2πr.
- Так как диаметр – это удвоенный радиус, периметр может быть найден по формуле: P = πd.
Реклама
-
1
Найдите длины двух сторон треугольника (а и b), пересекающихся под прямым углом.
-
2
Найдите сумму квадратов а и b, а затем извлеките квадратный корень из полученной суммы: √(а^2 + b^2). По теореме Пифагора, а^2 + b^2 = с^2, где с – длина гипотенузы, то есть стороны, лежащей напротив прямого угла.
-
3
Теперь, когда у вас есть а, b и с (все три стороны треугольника), просто сложите их для нахождения периметра: P = а+b+с.
Реклама
-
1
Найдите высоту треугольника (у) и его основание (х) (сторона, к которой проведен перпендикуляр – высота).
-
2
Найдите длины отрезков х1 и х2, на которые высота делит основание (то есть х = х1 + х2). Высота делит треугольник на два прямоугольных треугольника (один с катетами х1 и у, другой с катетами х2 и у), и необходимо найти длины гипотенуз этих треугольников с1 и с2.
-
3
Найдите с1 и с2. Для этого используйте теорему Пифагора: а^2 + b^2 = с^2, и подставьте x1 вместо a, y вместо b, c1 вместо c. Повторите для х2, у, и с2.
-
4
Сложите х, с1 и с2, которые являются тремя сторонами исходного треугольника.
Реклама
-
1
Найдите длину одной стороны правильного многоугольника. По определению, правильный многоугольник – это фигура с равными сторонами и углами.
- Если дана апофема (перпендикуляр, опущенный из центра многоугольника к одной из его сторон), Вы можете найти длину стороны. Если n – число сторон многоугольника, А – длина апофемы, длина стороны: x=2Atan(180/n).
- Если дан радиус (расстояние между центром и любой вершиной), вы можете найти длину стороны: x=2rsin(180/n), где r – радиус, n – число сторон многоугольника.
-
2
Умножьте длину одной стороны многоугольника на число его сторон. Таким образом, P=nx, где n – число сторон многоугольника, х – длина одной стороны многоугольника.
Реклама
Об этой статье
Эту страницу просматривали 16 039 раз.
Была ли эта статья полезной?
Основные определения
Наверное, каждый из нас сталкивался с треугольником. Это могло быть в школе, вузах, колледжах, на работе, во время помощи детям. Треугольник – это одна из самых простых геометрических фигур, но в то же время она выполняет очень важную роль. Множество свойств хранит треугольник. Но сегодня не будем вдаваться в подробности, а поговорим про периметр и порешаем задачи по нахождению его.
Если мы отметим на плоскости 3 точки и проведём к ним линии, то как раз получим треугольник.
Понятия
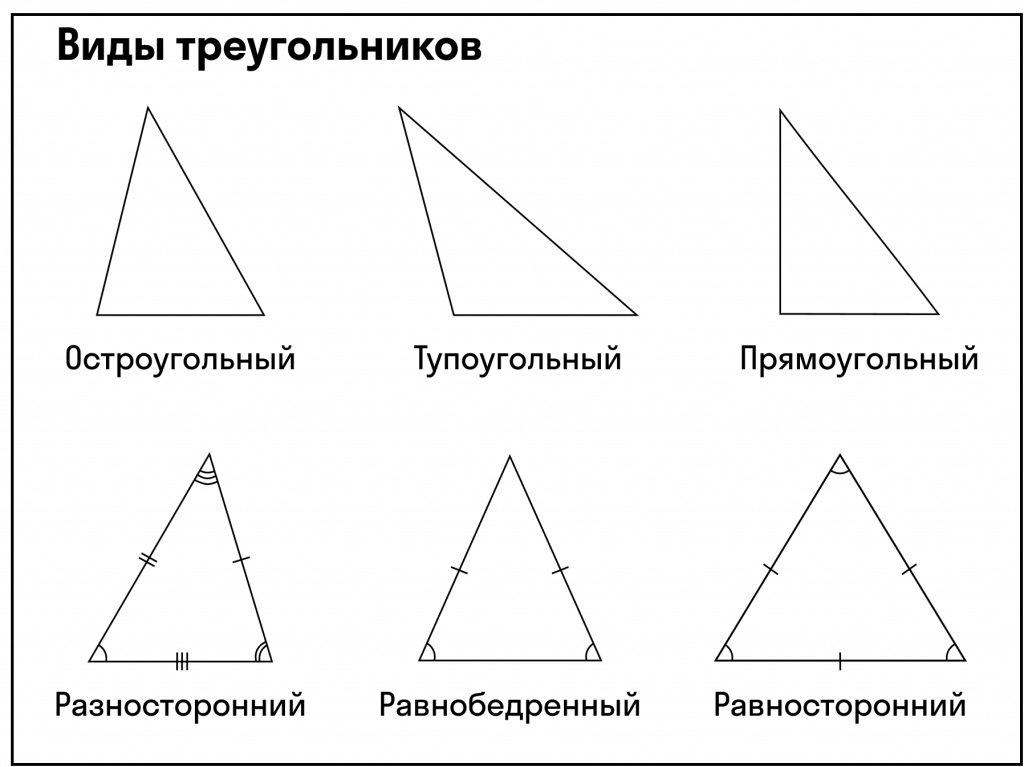
Треугольник – это геометрическая фигура, состоящая из трёх точек, которые соединены отрезками – сторонами. В зависимости от отношений между сторонами фигуры, то они бывают равносторонними, разносторонними и равнобедренными (р/б – равнобедренный, р/с – равносторонний).
Вершины треугольника – это точки, где соединяются 2 стороны фигуры.
Р/б треугольник – это треугольник у которого две стороны равны, но не равны третьей.
Р/с треугольник – это треугольник, у которого все стороны равны между собой.
Разносторонний треугольник – это треугольник, у которого все стороны не равны между собой.
Прямоугольный треугольник — это треугольник, у у которого один угол равен 90о. Самая длинная сторона называется гипотенузой, а две другие катетами.
Формула нахождения периметра
Из определения следует, что периметр геометрической фигуры – это сумма длин всех сторон, и треугольник не стал исключением. Общая формула имеет вид: Р = а + b + с. Периметр будет обозначаться Р. а, b и с — стороны треугольника. Решим задачу №1.
Задача 1
Пусть нам дан треугольник со сторонами 13 см, 15 см, 12 см. Нужно найти периметр данного треугольника.
Решение: [P=13+15+12=40] см.
Ответ: 40 см.
Периметр разностороннего треугольника
В прошлой задаче мы как раз нашли периметр разностороннего треугольника. Решим похожую задачу №2
Задача 2
Дан треугольник со сторонами 25 дм, 30 дм, 15 дм. Найдите периметр треугольника. Ответ выразите в метрах.
Решение:
P = 30 + 25 + 15 = 70 дм
70 : 10 = 7 м
Ответ: 7 м.
Периметр равнобедренного треугольника
Так как в р/б треугольнике 2 стороны равны (боковые), то формулу нахождения можно представить как: P = 2a + b. Решим 2 задачи.
Задачи 3 — 4
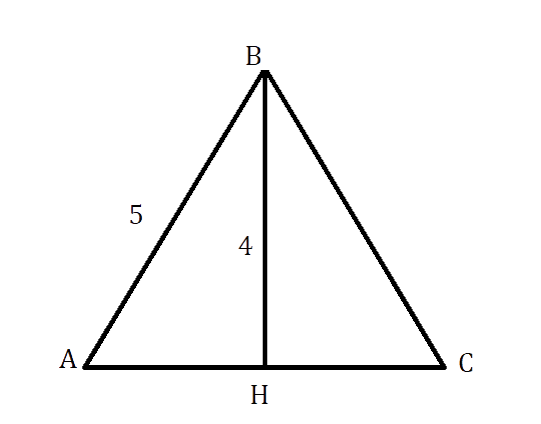
Дан равнобедренный треугольник АВС с биссектрисой, проведённой к основанию и равной 4 см, а также с боковой
стороной, равной 5 см. Найдите периметр данного треугольника.
Решение:
Так как ВН – биссектриса р/б треугольника АВС, то она является как высотой, так и медианой. Следовательно, ΔАВН прямоугольный и АН = НС.
В ΔАВН по теореме Пифагора [A H^{2}=A B^{2}-B H^{2}=25-16=9]см
АН = НС = √9 = 3 см
АС = АН + НС = 3 + 3 = 6 см
Р = 6 + 2*5 = 16 см
Ответ: 16 см.
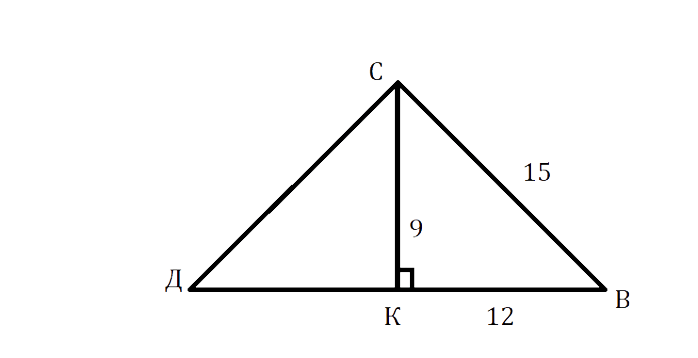
В треугольнике ДСВ ДС = СВ = 15 см, высота СК = 9 см. Найдите периметр этого треугольника.
Решение:
В ΔСКД по теореме Пифагора:
[text { ДК² }=text { ДС }^{2}-mathrm{CK}^{2}=225-81=144]см
ДК = √144 = 12 см.
Так как СК — высота в р/б треугольнике, проведённая к основанию, то она является медианой, следовательно, ДВ = ДК + КВ = 12 + 12 = 24 см.
Р = ДС + СВ + ДВ = 15 + 15 + 24 = 54 см.
Ответ: 54 см.
Нет времени решать самому?
Наши эксперты помогут!
Периметр равностороннего треугольника
А это один из самых “хороших” треугольников, его ещё называют правильным, так как все стороны и углы равны между собой. Формула нахождения периметра будет иметь вид: P = 3a.
Задачи 5 — 6
Дан равносторонний треугольник со стороной а = 13. Найдите периметр этого треугольника.
Решение:
Р = 3а = 3 * 13 = 39
Ответ: 39.
В равностороннем треугольнике АВС есть стороны: АВ = АС = СВ = 15 см, Найдите периметр данного треугольника.
Решение:
Р = 3АВ = 15 * 3 = 45 см.
Ответ: 45 см.
Периметр прямоугольного треугольника
Вычисляем по стандартной формуле: Р = а + в + с. Но у такого вида треугольников есть огромное преимущество – применение теоремы Пифагора.
Задачи 7 — 8
Дан прямоугольный треугольник с катетами а = 6 и в = 8. Найдите периметр.
Решение:
По теореме Пифагора: [c^{2}=в^{2}+a^{2}=64+36=100]
с = √100 = 10
Р = а + в + с = 6 + 8 + 10 = 24
Ответ: 24.
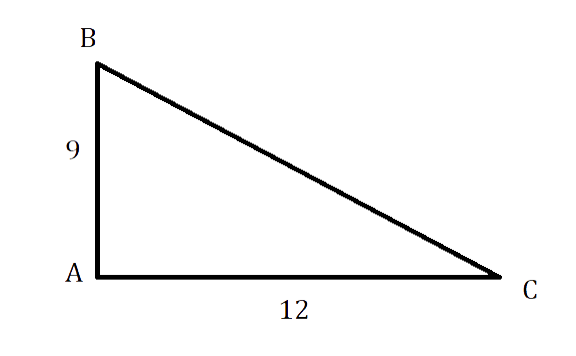
В прямоугольном треугольнике АВС, [angle mathrm{A}=90^{circ}, mathrm{AB}=9 mathrm{~см}, mathrm{AC} = 12см]. Надо найти периметр и площадь АВС.
Решение
По теореме Пифагора в ΔАВС:
[mathrm{CB}^{2}=mathrm{AC}^{2}+A mathrm{C}^{2}=144+81=225 mathrm{~см}]
СВ = √225 = 15 см
S = (АС * АВ) : 2 = (9 * 12) : 2 = 54 см
P = 15 + 9 + 12 = 36 см
Ответ: 36 см; 54 см.