Firstly, since they asked for the maximum, we know that AE must be equal to AF to maximise the perimeter. Then the figure would be symmetrical about the diagonal, so $∠ECB=∠DCF=frac{90^o-45^o}{2}=22.5^o$. Now $tan(22.5^o)=frac{EB}{BC}=frac{EB}{5}$.
We have $EB=2.07106…$, giving us $AE=AF=5-EB=2.92893…$. By Pythagoras’ theorem, $EF=sqrt{AE^2+AF^2}=4.1421…$.
Summing it all, $AE+AF+EF=10$. Strangely, this is a rather nice number. Currently working on a solution that does not require calculator.
Here is another approach which requires zero use of the calculator. Making use of the same approach as above, $AE=AF=5-5tan(22.5^o)$, and $EF=(5-5tan(22.5^o))sqrt{2}$. Our total sum is $10-10tan(22.5^o)+(5-5tan(22.5^o))sqrt{2}$. Our goal now would be to find the mysterious $tan(22.5^o)$.
We make use of the trigonometric identity $tan(2A)=frac{2tan(A)}{1-tan^2(A)}$. Noting that $tan(45^o)=1$, we let $2A=45^o$. We have, now, $1=frac{2tan(A)}{1-tan^2(A)}$. Solving this quadratic equation by letting $tan(A)=x$, we get $tan(22.5^o)=-1pmsqrt{2}$. Knowing that $tan(22.5^o)$ is positive, it is $-1+sqrt{2}$.
Substituting $tan(22.5^o)=-1+sqrt{2}$ into $10-10tan(22.5^o)+(5-5tan(22.5^o))sqrt{2}$, we get 10.
Периметр, формулы нахождения периметра
Периметр фигуры это длина всех ее сторон. Не все фигуры имеют периметр, например, шар не имеет периметра. Стандартное обозначение периметра в математике – буква P
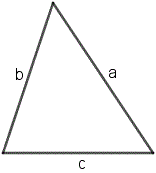
Периметр треугольника
Периметр квадрата
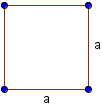
Пусть длина стороны квадрата равна a . Квадрат имеет четыре равных стороны, поэтому периметр квадрата есть P = a + a + a +a или:
Периметр прямоугольника

Пусть длины сторон прямоугольника равны a и b .
Длина всех его сторон есть P = a + b + a + b или:
Периметр параллелограмма
Пусть длины сторон параллелограмма равны a и b
Длина всех его сторон есть P = a + b + a + b , поэтому периметр параллелограмма есть:
Как видно, периметр параллелограмма равен периметру прямоугольника.
Периметр ромба
Периметр равнобедренной трапеции
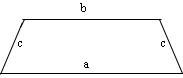
Пускай длины параллельных сторон трапеции a и b , а длины двух других сторон равна c (Как известно, равнобедренная трапеция имеет две равные стороны).
Периметр равностороннего треугольника
Как известно, равносторонний треугольник имеет 3 равные стороны. Если длина стороны равна a , тогда формула нахождения периметра есть P = a + a + a
Длина окружности(периметр круга)
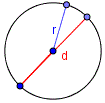
Обозначим длину окружности буквой l .
$l = d cdot pi = 2cdot r cdot pi$
Где:
$pi = 3,14$
r радиус круга (окружности)
d диаметр круга.
Правильный многоугольник
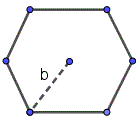
n число ребер(вершин).
$pi = 3,14159265359$
Формулы периметра геометрических фигур
Формула периметра треугольника

Периметр треугольника ∆ ABC равен сумме длин его сторон
Формулы периметра квадрата

Периметр квадрата равен произведению длины его стороны на четыре.
Периметр квадрата равен произведению длины его диагонали на два корня из двух.
Формула периметра прямоугольника

Периметр прямоугольника ABCD равен удвоенной сумме сторон, прилежащих к одному углу.
Формула периметра параллелограмма

Периметр параллелограмма ABCD равен удвоенной сумме сторон, прилежащих к одному углу
Формула периметра ромба

Периметр ромба равен произведению длины его стороны на четыре.
Формула периметра трапеции

Периметр трапеции равен сумме длин ее сторон.
Формулы длины окружности.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Как найти периметр фигуры

О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Определение периметра
Периметр — это сумма длин всех сторон многоугольника.
Какой буквой обозначается периметр? Заглавной латинской P. Под обозначением P удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.
В чем измеряется периметр? В тех же единицах измерения, что и длина — например, миллиметр, сантиметр, метр, фут, дюйм, локоть и др.
Если в условиях задачки длины сторон переданы в разных единицах длины, мы не сможем узнать периметр фигуры. Для правильного решения нужно перевести все данные в одну единицу измерения.
Формулы нахождения периметра
Как мы только что узнали, периметр — это сумма длин всех сторон многоугольника. А значит, чтобы его найти, нам надо знать длины этих сторон. Давайте посмотрим, как найти периметр, на примерах нескольких фигур.
Равносторонний многоугольник
У равностороннего треугольника все стороны равны. А значит, периметр равностороннего треугольника можно найти как произведение длины стороны на их количество, т. е. на 3.

P = 3 ⋅ a, где a — длина стороны.
Периметр любого другого равностороннего многоугольника можно найти тем же способом: умножив длину его стороны на их количество. Например, у квадрата и ромба все стороны равны, а значит, их периметр можно найти по формуле P = 4 ⋅ a, где a — длина стороны.
А формула для любого равностороннего n-угольника будет такая: P = n ⋅ a, где a — длина стороны, n — количество сторон.
Прямоугольник и параллелограмм
У прямоугольника и параллелограмма противоположные стороны равны, а значит, найти их периметр легко, зная две соседние стороны.
P = 2 ⋅ (a + b), где a — одна сторона, b — соседняя сторона.
Окружность
У окружности нет периметра, потому что это не многоугольник. Но у нее есть длина, которую можно найти, зная радиус. Длина окружности — это произведение пи на два радиуса или произведение пи на диаметр.
L = d ⋅ π = 2 ⋅ r ⋅ π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она приблизительно равна 3,14.
Можно выучить все формулы, а можно, запомнив определение о сумме всех сторон, каждый раз проявлять смекалку и вычислять самостоятельно. Давайте потренируемся, как определять периметр фигур!
Решение задач
Площадь прямоугольника равна 80 см 2 , длина составляет 10 см. Чему равен периметр фигуры?
- Для использования формулы P = 2 × (a + b), нам нужно найти ширину;
- Так как S = a × b, для поиска одной стороны необходимо разделить площадь на известную сторону: 80 : 10 = 8 см;
- Далее подставляем известные данные в формулу: (10 + 8) × 2 = 36 см;
Равнобедренный треугольник имеет периметр 40 см, длина его основания составляет 6 см. Какую длину будут иметь две другие стороны?
- Мы знаем, что периметр — это сумма длин всех сторон, а значит, если вычесть из данного периметра сторону основания — получим сумму двух оставшихся сторон: 40 − 6 = 34 см;
- Известно, что равнобедренный треугольник имеет две равные стороны;
- Далее делим получившуюся сумму на два: 34 : 2 = 17 см;
Ответ: две другие стороны равны по 17 см.
Радиус окружности равен периметру равностороннего пятиугольника со стороной 4 см. Найдите длину окружности.
- Периметр равностороннего пятиугольника равен 4 × 5 = 20 см, значит, радиус окружности равен 20 см;
- Длина окружности равна π × 2 × 20 = 40π см;
Еще больше практических заданий — на курсах по математике в онлайн-школе Skysmart!
[spoiler title=”источники:”]
http://ru.onlinemschool.com/math/formula/perimeter/
http://skysmart.ru/articles/mathematic/perimetr-figury
[/spoiler]
|
Как находить периметр геометрических фигур (треугольник, четырёхугольник, многоугольник) по известным координатам вершин? Какая формула должна использоваться? Формула для вычисления длины стороны АВ по известным координатам:
Аналогичным образом высчитываются остальные стороны, а затем полученные величины суммируются. автор вопроса выбрал этот ответ лучшим
Ксарфакс 4 года назад Периметр по координатам Периметр фигуры – это сумма длин всех её сторон. Чтобы в нашем случае найти длины сторон, нужно воспользоваться формулой длины отрезка по заданным координатам (x1; y1) и (x2; y2):
Последовательно складываем все полученные значения и получаем периметр. Если в задаче вид фигуры (квадрат, прямоугольник, равносторонний треугольник и т.п.) оговаривается заранее, то находить все длины может и не понадобиться. Например, периметр квадрата ABCD будет равен 4 * AB, так как у этой фигуры все стороны равны. То есть будет достаточно вычислить, чему равна сторона AB и умножить её на 4. Рассмотрим несколько примеров. 1) Треугольник ABC имеет координаты A(1,1); B(1,3); C(2,1). P(ABC) = AB + AC + BC. AB = √(0 + 2²) = √4 = 2. AC = √(1² + 0) = √1 = 1. BC = √(1² + (-2)²) = √5 ≈ 2,24. Таким образом, P(ABC) ≈ 2 + 1 + 2,24 = 5,24. 2) Прямоугольник ABCD имеет координаты A(2,1); B(2,4); C(3,4); C(3,1). P(ABCD) = 2AB + 2BC (так как по определению прямоугольника AB = CD и BC = AD). AB = √(0 + 3²) = √9 = 3. AC = √(1² + 0) = √1 = 1. Таким образом, P(ABC) = 3 * 2 + 1 * 2 = 8. ** Найти периметр по координатам можно и без использования формулы длины отрезка. Порядок действий такой:
Sadness 4 года назад Так как координаты вершин нам известны, то, для нахождения периметра, остаётся просто вычислить длину каждой стороны и сложить их. Длина отрезка вычисляется так:l=sqrt((x2 – x1)^2 + (y2 – y1)^2); Важно: вычитаем всегда начало из конца. Нахождение на примере:
Найдём длины всех трёх сторон и сложим. AB=sqrt((x2 – x1)^2 + (y2 – y1)^2)=sqrt((12 – 1)^2 + ((-5) – 8)^2)=sqrt(121 + 169)=sqrt(290); BC=sqrt((x2 – x1)^2 + (y2 – y1)^2)=sqrt((-2 – 12)^2 + (1 – -(5))^2)=sqrt(196 + 36)=sqrt(232); CA=sqrt((1 – (-2))^2 + (8 – 1)^2)=sqrt(9 + 49)=sqrt(58); Далее просто складываем полученные результаты: P=AB+BC+CA; Ну вот и всё, так просто находится периметр по заданным координатам(для любой фигуры). P.s извиняюсь за плохо подобранные координаты.
Давайте сначала вспомним, что такое периметр фигуры и как его вычислить. Периметром называется сумма длин всех сторон данной фигуры. Таким образом, для вычисления периметра какой-либо фигуры нужно знать длину всех ее сторон. Затем дело останется за малым – просто сложить длины. По сути, сторона любого многоугольника ( треугольника, четырехугольника, пятиугольника и так далее ) представляется собой отрезок. Для вычисления длины отрезка по координатом его концов используется следующая формула:
, где х1 и х2 – координаты концов отрезка по оси х, а y1 и y2 – координаты по оси у. Подставляем в формулу значения, проводим вычисления. Находим длину каждой из сторон. Суммируем все длины.
Hamster1337 2 года назад Периметр геометрических фигур по координатам вершин можно найти при помощи формулы
Где x1,x2 это первая координата, y1,y2 это вторая координата. Данную формулу нужно применять к каждой паре соседних вершин многоугольника. После обхода и суммирования всех длин будет получен периметр.
Алиса в Стране 3 года назад Любая геометрическая фигура это совокупность отрезков, составляющих ее стороны, и вершин а ее периметр – сумма длин этих отрезков, сумма сторон, поэтому если мы найдем длины всех сторон и сложим их, то получим как раз периметр фигуры. Для того, чтобы найти длину отрезка АВ, зная его координаты, есть такая вот формула:
где точка А имеет координаты (x1; y1), а точка В – координаты (x2; y2). Итак, длину отрезка мы находить научились. Допустим теперь, что у нас есть треугольник АВС, мы знаем координаты его вершин, по указанной выше формуле мы находим длины отрезков АВ, ВС, АС и складываем их, получая периметр этого треугольника АВС: АВ + ВС + АС.
габбас 4 года назад Периметр любого многоугольника вычисляется как сумма длин всех его сторон. Значит задача сводится к нахождению длины отрезка по координатам его концов. А это известная формула из курса геометрии основной школы. Итак, длина отрезка d = sqrt(x2^2 – x1^2) + (y2^2 – y1^2), х1 и у1 координаты начала, х2,у2 – координаты конца отрезка. Таким образом находим длины всех сторон многоугольника и суммируем эти значения. Лара Изюминка 3 года назад Во-первых, вспомним, что такое периметр – это сумма длин сторон. То есть нам нужны длины сторон многоугольника. Чтобы их найти, зная координаты точек, воспользуемся формулой из геометрии для нахождения расстояния между двумя точками на плоскости: AB = √(xb – xa)2 + (yb – ya)2. То есть нужно вычислить корень квадратный из суммы квадратов разницы координат по х и по у. Если фигура в пространстве, то добавится еще разница координат по z. AB = √(xb – xa)2 + (yb – ya)2 + (zb – za)2 Когда длины всех отрезков найдем остается их только сложить. Периметром фигуры зовется сумма длин всех сторон. Для поиска длинны сторон воспользуйтесь формулой длинны отрезка согласно координатам, которые заданы. (x1; y1) и (x2; y2):
Так, если вы последовательно сложите значения, которые получите, то сможете получить периметр. Что касается примеров, при условии наличия координат по точкам А (4;2), В(-6;-3), С(0;8) Следует сложить – получить.
Бекки Шарп 3 года назад Если геометрическая фигура находится в системе координат и координаты ее вершин известны, то длину сторон будем искать по такой формуле:
У нас есть треугольник. Координаты его точек- А (4;2), В(-6;-3), С(0;8) Находим длины отрезков АВ, ВС и АС по формуле.
Складываем полученные результаты и получаем периметр.
Бархатные лапки 3 года назад Существует формула, по которой можно вычислить длину отрезка, если известны координаты. Делим нашу геометрическую фигуру на отрезки, считаем длину каждого отрезка и затем все значения длин складываем. Таким образом мы получаем периметр.
Знаете ответ? |
Выбирайте формулу в зависимости от известных величин.
1. Как найти периметр треугольника, зная три стороны
Просто посчитайте сумму всех сторон.
- P — искомый периметр;
- a, b, c — стороны треугольника.
2. Как найти периметр треугольника, зная его площадь и радиус вписанной окружности
Умножьте площадь треугольника на 2.
Разделите результат на радиус вписанной окружности.
- P — искомый периметр;
- S — площадь треугольника;
- r — радиус вписанной окружности.
3. Как вычислить периметр треугольника, зная две стороны и угол между ними
Сначала найдите неизвестную сторону треугольника с помощью теоремы косинусов:
- Умножьте одну сторону на вторую, на косинус угла между ними и на 2.
- Посчитайте сумму квадратов известных сторон и отнимите от неё число, полученное в предыдущем действии.
- Найдите корень из результата.
Теперь прибавьте к найденной стороне две ранее известные стороны.
- P — искомый периметр;
- b, c — известные стороны треугольника;
- ɑ — угол между известными сторонами;
- a — неизвестная сторона треугольника.
4. Как найти периметр равностороннего треугольника, зная одну сторону
Умножьте сторону на 3.
- P — искомый периметр;
- a — любая сторона треугольника (напомним, в равностороннем треугольнике все стороны равны).
5. Как вычислить периметр равнобедренного треугольника, зная боковую сторону и основание
Умножьте боковую сторону на 2.
Прибавьте к результату основание.
- P — искомый периметр;
- a — боковая сторона треугольника (в равнобедренном треугольнике боковые стороны равны);
- b — основание треугольника (это сторона, которая отличается длиной от остальных).
6. Как найти периметр равнобедренного треугольника, зная боковую сторону и высоту
Найдите квадраты боковой стороны и высоты.
Отнимите от первого числа второе.
Найдите корень из результата и умножьте его на 2.
Прибавьте к полученному числу две боковые стороны.
- P — искомый периметр;
- a — боковая сторона треугольника;
- h — высота (перпендикуляр, опущенный на основание треугольника со стороны противоположной вершины; в равнобедренном треугольнике высота делит основание пополам).
7. Как вычислить периметр прямоугольного треугольника, зная катеты
Найдите квадраты катетов и посчитайте их сумму.
Извлеките корень из полученного числа.
Прибавьте к результату оба катета.
- P — искомый периметр;
- a, b — катеты треугольника (стороны, которые образуют прямой угол).
8. Как найти периметр прямоугольного треугольника, зная катет и гипотенузу
Посчитайте квадраты гипотенузы и катета.
Отнимите от первого числа второе.
Найдите корень из результата.
Прибавьте катет и гипотенузу.
- P — искомый периметр;
- a — любой катет прямоугольника;
- c — гипотенуза (сторона, которая лежит напротив прямого угла).
Содержание материала
- Формула
- Видео
- Периметр треугольника
- Что такое периметр?
- Площадь квадрата
- Перевод единиц измерения площади
- Нахождение периметра параллелограмма
- Нахождение периметра многоугольника
- Решение задач
Формула
Чтобы найти периметр треугольника $ABC$, необходимо сложить длины всех его сторон.
Напомним, что периметр треугольника — это сумма длин всех его сторон. То есть если задан произвольный треугольник $ABC$ и длины его сторон соответственно равны $AB=c$, $AC=b$, $BC=a$, то периметр треугольника вычисляется по формуле:
$$P_{Delta A B C}=a+b+c$$

Видео
Периметр треугольника
Треугольником следует называть геометрическую фигуру, имеющую три угла (как разного значения, так и одинакового) и состоящую из отрезков, образованных от точек пересечения лучей, образующих углы. Треугольник имеет три стороны и три угла. В нем могут быть из трех равны две стороны. Такой треугольник следует считать равнобедренным. Бывают такие фигуры, в которых равны все три стороны между собой. Принято такие треугольники называть равносторонними.
Что такое периметр треугольника? Его вычисление можно провести по аналогии с периметром четырехугольника. Равен периметр треугольника суммарной длине длин его сторон. Вычисление периметра треугольника, в котором две стороны равны – равнобедренного – упрощается умножением одной длины равных сторон на два. К полученному значению необходимо прибавить значение длины третьей стороны. Вычисление периметра треугольника с равными сторонами можно свести к простому вычислению произведения одной длины стороны треугольника на три.
Читать еще: Тест нарисовать дом дерево человека расшифровка пример. Методика исследования личности «Дом-дерево-человек» Дж

Что такое периметр?
Периметром называют суммарную длину всех сторон геометрической фигуры. Для его обозначения используется буква латинского алфавита «Р». Проще говоря, чтобы найти периметр, необходимо измерить длины всех сторон геометрической фигуры и сложить полученные значения. Длина вычисляется обычным измерительным прибором, таким как линейка, рулетка, сантиметровая лента и прочее.
Единицей измерения соответственно являются сантиметры, метры, миллиметры и другие меры длины. Длина стороны многоугольника вычисляется путем прикладывания измерительного прибора от одной вершины к другой. Начало шкалы деления прибора должно совпадать с одной из вершин. Второе числовое значение, на которое попадает другая вершина и является длиной стороны многоугольника. Таким же образом необходимо измерить все длины сторон фигуры и полученные значения сложить. Единицей измерения периметра является та же самая единица, которая используется для измерения стороны фигуры.
Площадь квадрата
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, на следующем рисунке представлен квадрат со стороной 3 см. Фраза «квадрат со стороной 3 см» означает, что все стороны равны 3 см

Площадь квадрата вычисляется таким же образом, как и площадь прямоугольника — длину умножают на ширину.
Вычислим площадь квадрата со стороной 3 см. Умножим длину 3 см на ширину 3 см
3 × 3 = 9
В данном случае требовалось узнать сколько квадратов со стороной 1 см содержится в исходном квадрате. В исходном квадрате содержится девять квадратов со стороной 1 см. Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз:

Умножив длину на ширину, мы получили выражение 3 × 3, а это есть произведение двух одинаковых множителей, каждый из которых равен 3. Иными словами выражение 3 × 3 представляет собой вторую степень числа 3. А значит процесс вычисления площади квадрата можно записать в виде степени 32.
Поэтому вторую степень числа называют квадратом числа. При вычислении второй степени числа a, человек тем самым находит площадь квадрата со стороной a. Операцию возведения числа во вторую степень по другому называют возведением в квадрат.
Перевод единиц измерения площади
Единицы измерения площади можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:
Пример 1. Выразить 1 квадратный метр в квадратных сантиметрах.
1 квадратный метр это квадрат со стороной 1 м. То есть все четыре стороны имеют длину, равную одному метру.

Но 1 м = 100 см. Тогда все четыре стороны тоже имеют длину, равную 100 см

Вычислим новую площадь этого квадрата. Умножим длину 100 см на ширину 100 см или возведём в квадрат число 100
S = 1002 = 10 000 см2
Получается, что на один квадратный метр приходится десять тысяч квадратных сантиметров.
1 м2 = 10 000 см2
Это позволяет в будущем умножить любое количество квадратных метров на 10 000 и получить площадь, выраженную в квадратных сантиметрах.
Чтобы перевести квадратные метры в квадратные сантиметры, нужно количество квадратных метров умножить на 10 000.
А чтобы перевести квадратные сантиметры в квадратные метры, нужно наоборот количество квадратных сантиметров разделить на 10 000.
Например, переведём 100 000 см2 в квадратные метры. Рассуждать в этом случае можно так: «если 10 000 см2 это один квадратный метр, то сколько раз 100 000 см2 будут содержать по 10 000 см2»
100 000 см2 : 10 000 см2 = 10 м2
Другие единицы измерения можно переводить таким же образом. Например, переведём 2 км2 в квадратные метры.
Один квадратный километр это квадрат со стороной 1 км. То есть все четыре стороны имеют длину, равную одному километру. Но 1 км = 1000 м. Значит, все четыре стороны квадрата также равны 1000 м. Найдём новую площадь квадрата, выраженную в квадратных метрах. Для этого умножим длину 1000 м на ширину 1000 м или возведём в квадрат число 1000
S = 10002 = 1 000 000 м2
Получается, что на один квадратный километр приходится один миллион квадратных метров:
1 км2 = 1 000 000 м2
Это позволяет в будущем умножить любое количество квадратных километров на 1 000 000 и получить площадь, выраженную в квадратных метрах.
Чтобы перевести квадратные километры в квадратные метры, нужно количество квадратных километров умножить на 1 000 000.
Итак, вернёмся к нашей задаче. Требовалось перевести 2 км2 в квадратные метры. Умножим 2 км2 на 1 000 000
2 км2 × 1 000 000 = 2 000 000 м2
А чтобы перевести квадратные метры в квадратные километры, нужно наоборот количество квадратных метров разделить на 1 000 000.
Например, переведём 3 500 000 м2 в квадратные километры. Рассуждать в этом случае можно так: «если 1 000 000 м2 это один квадратный километр, то сколько раз 3 500 000 м2 будут содержать по 1 000 000 м2»
3 500 000 м2 : 1 000 000 м2 = 3,5 км2
Пример 2. Выразить 7 м2 в квадратных сантиметрах.
Умножим 7 м2 на 10 000
7 м2 = 7 м2 × 10 000 = 70 000 см2
Пример 3. Выразить 5 м2 13 см2 в квадратных сантиметрах.
5 м2 13 см2 = 5 м2 × 10 000 + 13 см2 = 50 013 см2
Пример 4. Выразить 550 000 см2 в квадратных метрах.
Узнаем сколько раз 550 000 см2 содержит по 10 000 см2. Для этого разделим 550 000 см2 на 10 000 см2
550 000 см2 : 10 000 см2 = 55 м2
Пример 5. Выразить 7 км2 в квадратных метрах.
Умножим 7 км2 на 1 000 000
7 км2 × 1 000 000 = 7 000 000 м2
Пример 6. Выразить 8 500 000 м2 в квадратных километрах.
Узнаем сколько раз 8 500 000 м2 содержит по 1 000 000 м2. Для этого разделим 8 500 000 м2 на 1 000 000 м2
8 500 000 м2 × 1 000 000 м2 = 8,5 км2
Нахождение периметра параллелограмма
Определение
Параллелограмм – это такой четырехугольник, у которого противоположные стороны порно параллельны.
Характеристики:
- Противоположные стороны равны.
- Противоположные углы равны.
- Диагонали в точке пересечения делятся пополам.
- Как и в прямоугольнике, диагональ параллелограмма делит его на 2 треугольника.
- Два угла на одной стороне равны 180°

Периметр параллелограмма находится точно так же, как и периметр прямоугольника:
[P = a + a + b + b]
[P = 2(a + b)]
[P = 2a + 2b]
Нахождение периметра многоугольника
Определение
Многоугольник – это геометрическая фигура, которая со всех сторон ограничена ломанной линией.
Характеристики:
- Название многоугольника определяется количеством его вершин. Если у многоугольника количество вершин равно n, то он называется n-угольником.
- Многоугольником являются такие фигуры, как: квадрат, ромб, параллелограмм и т.д.
- Если углы с отрезками равны, то это правильный многоугольник.

Чтобы найти периметр n-угольника, нужно сложить всего длины его сторон:
[P = a1 + a2 + … an]
А для правильного n-угольника можно выделить еще одну формулу, потому как его стороны равны:
P = na
Здесь мы умножаем длину одной стороны на n.
Пример 1
Найдите периметр правильного многоугольника, если у него 5 вершин, а длина его одной стороны равна 7.
Решение:
Здесь воспользуемся этой формулой:
P = na
7 × 5 = 35 (см)
Ответ: периметр многоугольника равняется 35 см.
Решение задач
Площадь прямоугольника равна 80 см2, длина составляет 10 см. Чему равен периметр фигуры?
Как решаем:
- Для использования формулы P = 2 × (a + b), нам нужно найти ширину;
- Так как S = a × b, для поиска одной стороны необходимо разделить площадь на известную сторону: 80 : 10 = 8 см;
- Далее подставляем известные данные в формулу: (10 + 8) × 2 = 36 см;
Ответ: 36 см.
Равнобедренный треугольник имеет периметр 40 см, длина его основания составляет 6 см. Какую длину будут иметь две другие стороны?
Как решаем:
- Мы знаем, что периметр — это сумма длин всех сторон, а значит, если вычесть из данного периметра сторону основания — получим сумму двух оставшихся сторон: 40 − 6 = 34 см;
- Известно, что равнобедренный треугольник имеет две равные стороны;
- Далее делим получившуюся сумму на два: 34 : 2 = 17 см;
Ответ: две другие стороны равны по 17 см.
Радиус окружности равен периметру равностороннего пятиугольника со стороной 4 см. Найдите длину окружности.
Как решаем:
- Периметр равностороннего пятиугольника равен 4 × 5 = 20 см, значит, радиус окружности равен 20 см;
- Длина окружности равна π × 2 × 20 = 40π см;
Ответ: 40π см.
Еще больше практических заданий — на курсах по математике в онлайн-школе Skysmart!













