Нахождение периметра треугольника: формула и задачи
В данной публикации мы рассмотрим, каким образом можно посчитать периметр треугольника и разберем примеры решения задач.
Формула вычисления периметра
Периметр (P) любого треугольника равняется сумме длин всех его сторон.
P = a + b + c
Периметр равнобедренного треугольника
Равнобедренным называют треугольник, у которого две боковые стороны равны (примем их за b). Сторона a, имеющая отличную от боковых длину, является основанием. Таким образом, периметр можно считать так:
P = a + 2b
Периметр равностороннего треугольника
Равносторонним или правильным называется треугольник, у которого все стороны равны (примем ее за a). Периметр такой фигуры вычисляется так:
P = 3a
Примеры задач
Задание 1
Найдите периметр треугольника, если его стороны равны: 3, 4 и 5 см.
Решение:
Подставляем в формулу известные по условиям задачи величины и получаем:
P = 3 см + 4 см + 5 см = 12 см.
Задание 2
Найдите периметр равнобедренного треугольника, если его основание равняется 10 см, а боковая сторона- 8 см.
Решение:
Как мы знаем, боковые стороны равнобедренного треугольника равны, следовательно:
P = 10 см + 2 ⋅ 8 см = 26 см.
Как посчитать периметр треугольника
Онлайн калькулятор
Периметр разностороннего треугольника
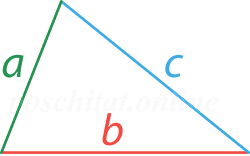
Чтобы вычислить чему равен периметр разностороннего треугольника вам нужно знать следующие параметры:
Введите их в соответствующие поля и узнаете чему равен периметр треугольника (Р).
Теория
Чему равен периметр разностороннего треугольника (P)?
Формула
Пример
К примеру, определим периметр разностороннего треугольника, у которого сторона a = 2 см, сторона b = 3 см, а сторона c = 4 см:
Периметр равнобедренного треугольника
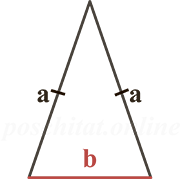
Чтобы вычислить чему равен периметр равнобедренного треугольника вам нужно знать следующие параметры:
- длину двух равных сторон (a)
- длину основания (b)
Теория
Чему равен периметр равнобедренного треугольника (P)?
Формула
Пример
К примеру, определим периметр равнобедренного треугольника, у которого стороны a = 2 см, а сторона b = 3 см:
Периметр равностороннего треугольника
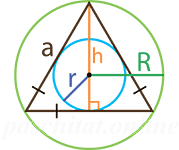
Чтобы вычислить чему равен периметр равностороннего треугольника вам нужно знать следующие параметры (либо-либо):
- длину трёх равных сторон (a)
- радиус описанной окружности (R)
- радиус вписанной окружности (r)
Как найти периметр треугольника
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение
Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской буквой P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах и ходе решении.
Важно, чтобы все параметры были переданы в одной единице длины, иначе мы не сможем подсчитать результат. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
В чем измеряется периметр:
Как узнать периметр треугольника
Рассмотрим какие существуют формулы, и при каких известных исходных данных их можно применять.
Если известны три стороны, то периметр треугольника равен их сумме. Этот способ проходят во втором классе.
P = a + b + c, где a, b, c — длина стороны.
Если известна площадь и радиус вписанной окружности:
P = 2 * S : r, где S — площадь, r — радиус вписанной окружности.
Если известны две стороны и угол между ними, вычислить периметр треугольника можно так:
P = √ b 2 + с 2 – 2 * b * с * cosα + (b + с), где b, с — известные стороны, α — угол между известными сторонами.
Если известна одна сторона в равностороннем треугольнике:
P = 3 * a, где a — длина стороны.
Все стороны в равносторонней фигуре равны.
Если известна боковая сторона и основание в равнобедренном треугольнике:
P = 2 * a + b, где a — боковая сторона, b — основание.
Боковые стороны в равнобедренной фигуре равны.
Если известна боковая сторона и высота в равнобедренном треугольнике:
P = 2 * (√ a 2 + h 2 ) + 2 * a, где a — боковая сторона, h — высота.
Высотой принято называть отрезок, который вышел из вершины и опустился на основание. В равнобедренной фигуре высота делит основание пополам.
Если известны катеты в прямоугольном треугольнике:
P = √ a 2 + b 2 + (a + b), где a, b — катеты.
Катет — одна из двух сторон, которые образуют прямой угол.
Если известны катет и гипотенуза в прямоугольном треугольнике:
P = √ c 2 – a 2 + (a + c), где a — любой катет, c — гипотенуза.
Гипотенуза — сторона, которая лежит напротив прямого угла.
Скачать онлайн таблицу
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
[spoiler title=”источники:”]
http://poschitat.online/perimetr-treugolnika
http://skysmart.ru/articles/mathematic/perimetr-treugolnika
[/spoiler]
Поможем понять и полюбить математику
Начать учиться
Как найти периметр треугольника
Многим формулам поиска периметра учат в 3 классе. Это фундаментальные знания, которые будут пригождаться на протяжении всех лет обучения в школе, и даже в вузе при выборе математического факультета. В этой статьем рассмотрим, как находить периметр треугольника.
Определение
Периметром принято называть сумму длин всех сторон многоугольника. Периметр обозначается заглавной латинской буквой P. Под P удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах и ходе решении.
Важно, чтобы все значения были заданы в одной единице измерения длины, иначе мы не сможем подсчитать результат. Поэтому для правильного решения необходимо привести все данные к одной единице измерения.
Часто встречающиеся единицы измерения периметра:
-
миллиметр (мм);
-
сантиметр (см);
-
дециметр (дм);
-
метр (м);
-
километр (км).
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Как узнать периметр треугольника
Рассмотрим, какие существуют формулы и при каких известных исходных данных их можно применять.
-
Если известны три стороны, то периметр треугольника равен сумме их длин.
Этот способ обычно проходят во втором классе.
P = a + b + c, где a, b, c — длина стороны.
-
Если известна площадь и радиус вписанной окружности:
P = 2S / r, где S — площадь, r — радиус вписанной окружности.
-
Если известна одна сторона в равностороннем треугольнике:
P = 3a, где a — длина стороны.
Все стороны в равносторонней фигуре равны.
-
Если известна боковая сторона и основание в равнобедренном треугольнике:
P = 2a + b, где a — боковая сторона, b — основание.
Боковые стороны в равнобедренном треугольнике равны.
-
Если известна боковая сторона и высота в равнобедренном треугольнике:
, где a — боковая сторона, h — высота, проведенная к основанию.
Высота — перпендикуляр, опущенный из вершины треугольника на противолежащую сторону. В равнобедренном треугольнике, высота, проведенная к основанию, является медианой, т. е. делит сторону пополам.
-
Если известны катеты в прямоугольном треугольнике:
, где a, b — катеты.
Катет — одна из двух сторон, которые образуют прямой угол.
-
Если известны катет и гипотенуза в прямоугольном треугольнике:
, где a — любой катет, c — гипотенуза.
Гипотенуза — сторона, которая лежит напротив прямого угла.
Скачать онлайн таблицу
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Выбирайте формулу в зависимости от известных величин.
1. Как найти периметр треугольника, зная три стороны
Просто посчитайте сумму всех сторон.
- P — искомый периметр;
- a, b, c — стороны треугольника.
2. Как найти периметр треугольника, зная его площадь и радиус вписанной окружности
Умножьте площадь треугольника на 2.
Разделите результат на радиус вписанной окружности.
- P — искомый периметр;
- S — площадь треугольника;
- r — радиус вписанной окружности.
3. Как вычислить периметр треугольника, зная две стороны и угол между ними
Сначала найдите неизвестную сторону треугольника с помощью теоремы косинусов:
- Умножьте одну сторону на вторую, на косинус угла между ними и на 2.
- Посчитайте сумму квадратов известных сторон и отнимите от неё число, полученное в предыдущем действии.
- Найдите корень из результата.
Теперь прибавьте к найденной стороне две ранее известные стороны.
- P — искомый периметр;
- b, c — известные стороны треугольника;
- ɑ — угол между известными сторонами;
- a — неизвестная сторона треугольника.
4. Как найти периметр равностороннего треугольника, зная одну сторону
Умножьте сторону на 3.
- P — искомый периметр;
- a — любая сторона треугольника (напомним, в равностороннем треугольнике все стороны равны).
5. Как вычислить периметр равнобедренного треугольника, зная боковую сторону и основание
Умножьте боковую сторону на 2.
Прибавьте к результату основание.
- P — искомый периметр;
- a — боковая сторона треугольника (в равнобедренном треугольнике боковые стороны равны);
- b — основание треугольника (это сторона, которая отличается длиной от остальных).
6. Как найти периметр равнобедренного треугольника, зная боковую сторону и высоту
Найдите квадраты боковой стороны и высоты.
Отнимите от первого числа второе.
Найдите корень из результата и умножьте его на 2.
Прибавьте к полученному числу две боковые стороны.
- P — искомый периметр;
- a — боковая сторона треугольника;
- h — высота (перпендикуляр, опущенный на основание треугольника со стороны противоположной вершины; в равнобедренном треугольнике высота делит основание пополам).
7. Как вычислить периметр прямоугольного треугольника, зная катеты
Найдите квадраты катетов и посчитайте их сумму.
Извлеките корень из полученного числа.
Прибавьте к результату оба катета.
- P — искомый периметр;
- a, b — катеты треугольника (стороны, которые образуют прямой угол).
8. Как найти периметр прямоугольного треугольника, зная катет и гипотенузу
Посчитайте квадраты гипотенузы и катета.
Отнимите от первого числа второе.
Найдите корень из результата.
Прибавьте катет и гипотенузу.
- P — искомый периметр;
- a — любой катет прямоугольника;
- c — гипотенуза (сторона, которая лежит напротив прямого угла).
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Геометрия
- Треугольник и его виды
Треугольник – это геометрическая фигура, состоящая из трех точек, которые не лежат на одной прямой, и трех отрезков, последовательно соединяющих эти точки. Указанные точки называются вершинами треугольника, а отрезки – сторонами.
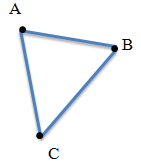
Данная фигура является треугольником (произносят: треугольник АВС, пишут: ∆ АВС). Точки А, В, С – вершины треугольника, а отрезки АВ, ВС, АС ‒ стороны.
Периметр треугольника – это сумма длин всех его сторон.
Виды треугольников
По виду углов:
- Остроугольный треугольник – это треугольник, у которого все три угла острые.
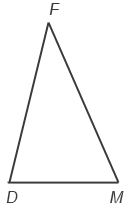
- Тупоугольный треугольник – это треугольник, у которого один из углов тупой.
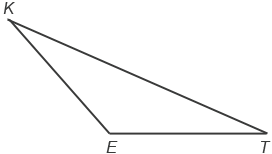
- Прямоугольный треугольник – это треугольник, у которого один из углов прямой.
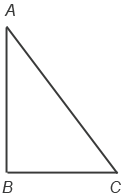
Сумма углов любого треугольника равна 1800.
По количеству равных сторон:
- Равнобедренный треугольник – это треугольник, у которого две стороны равны.
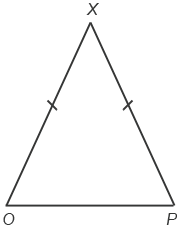
∆OXP – равнобедренный: XO = XP. Равные стороны на рисунке отмечают равным количеством чёрточек (в нашем случае одной чёрточкой). В равнобедренном треугольники равные стороны называют боковыми сторонами, а третью сторону – основанием, т.е. в ∆OXP: XO и XP – боковые стороны, а OP – основание.
- Равносторонний треугольник – это треугольник, у которого все стороны равны.
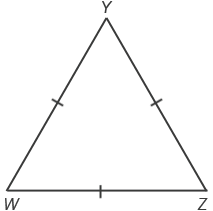
∆WYZ – равносторонний: WY = YZ = ZW. Равносторонний треугольник также называют правильным. Если сторона равностороннего треугольника равна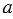 
, то его периметр вычисляют по формуле:
P = 3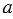
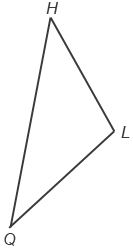
- Разносторонний треугольник – это треугольник, у которого все стороны имеют различную длину.
Советуем посмотреть:
Отрезок
Ломаная
Четырехугольники
Единицы измерения площадей. Свойства площадей
Прямоугольник, его периметр и площадь. Ось симметрии фигуры
Квадрат. Периметр и площадь квадрата.
Многоугольники. Правильные многоугольники. Равенство фигур.
Плоскость
Прямая
Луч
Шкалы и координаты
Прямоугольный параллелепипед. Пирамида.
Объем прямоугольного параллелепипеда
Куб. Площадь поверхности куба
Куб. Объем куба
Угол. Обозначение углов
Прямой и развернутый угол
Чертежный треугольник
Измерение углов. Транспортир. Виды углов
Окружность, круг, шар
Цилиндр, конус
Отрезок-xx
Геометрия
Правило встречается в следующих упражнениях:
5 класс
Задание 81,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 209,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1668,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1810,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 351,
Мерзляк, Полонский, Якир, Учебник
Номер 352,
Мерзляк, Полонский, Якир, Учебник
Номер 888,
Мерзляк, Полонский, Якир, Учебник
Номер 9,
Мерзляк, Полонский, Якир, Учебник
Номер 3,
Мерзляк, Полонский, Якир, Учебник
Номер 5,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 299,
Мерзляк, Полонский, Якир, Учебник
Номер 713,
Мерзляк, Полонский, Якир, Учебник
Номер 717,
Мерзляк, Полонский, Якир, Учебник
Номер 1225,
Мерзляк, Полонский, Якир, Учебник
Номер 1257,
Мерзляк, Полонский, Якир, Учебник
Номер 1267,
Мерзляк, Полонский, Якир, Учебник
Номер 1317,
Мерзляк, Полонский, Якир, Учебник
Номер 3,
Мерзляк, Полонский, Якир, Учебник
Задание 365,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1571,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 753,
Мерзляк, Полонский, Якир, Учебник
Номер 980,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 433,
Мерзляк, Полонский, Якир, Учебник
Номер 453,
Мерзляк, Полонский, Якир, Учебник
Номер 456,
Мерзляк, Полонский, Якир, Учебник
Номер 459,
Мерзляк, Полонский, Якир, Учебник
Периметр треугольника калькулятор онлайн умеет вычислять периметр восемью способами:
- По трем сторонам.
- По площади и радиусу вписанной окружности.
- По двум сторонам и углу между ними.
- По стороне равностороннего треугольника.
- По боковой стороне и основанию равнобедренного треугольника.
- По боковой стороне и высоте равнобедренного треугольника.
- По катетам прямоугольного треугольника.
- По одному катету и гипотенузе прямоугольного треугольника.
Сделав расчет периметра на этом онлайн калькуляторе Вы получите не только ответ, но и детальное, пошаговое решение с выводом формул и промежуточных действий.
Периметр треугольника- это сумма трех сторон.
Периметр может быть найден и по другим формулам, вывод которых основан на поиске длины неизвестной стороны.
Как найти периметр треугольника?
Найти периметр треугольника очень просто на нашем онлайн калькуляторе. Так же периметр может быть найден самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.
1) По трем сторонам
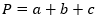
где a,b,c – стороны треугольника.
2) По площади и радиусу вписанной окружности
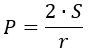
где S – площадь треугольника, r – радиус вписанной окружности.
3) По двум сторонам и углу между ними
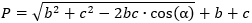
где b,c – стороны треугольника, α° – угол между ними.
4) По стороне равностороннего треугольника
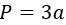
где a – сторона равностороннего треугольника.
5) По боковой стороне и основанию равнобедренного треугольника
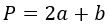
где a – боковая сторона и b – основание равнобедренного треугольника.
6) По боковой стороне и высоте равнобедренного треугольника
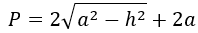
где a – боковая сторона и h – высота равнобедренного треугольника.
7) По катетам прямоугольного треугольника
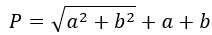
где a,b – катеты прямоугольного треугольника.
8) По одному катету и гипотенузе прямоугольного треугольника.
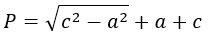
где а – катет и с – гипотенуза прямоугольного треугольника.
Скачать все формулы в формате Word
