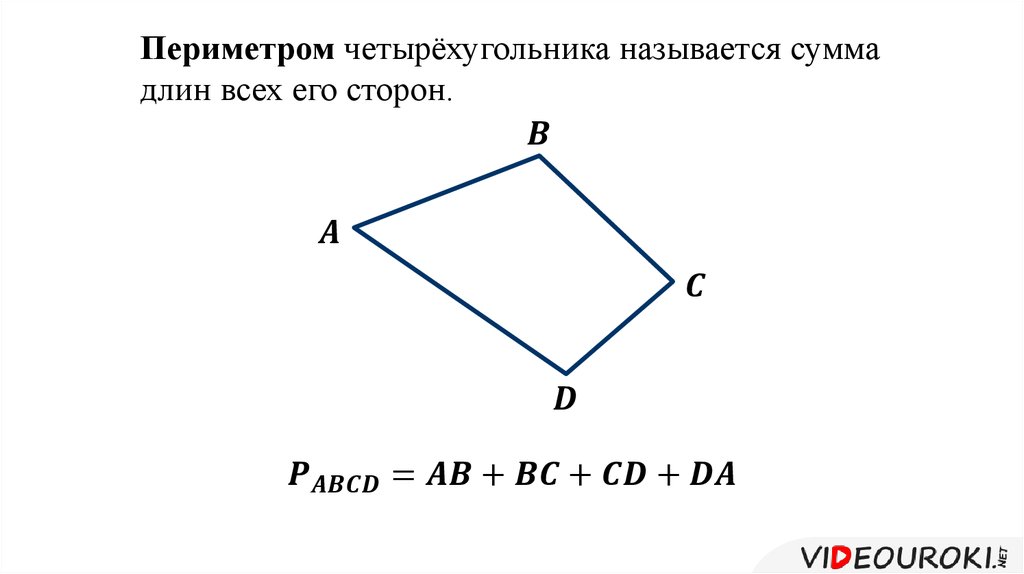
Периметр четырехугольника
Вы будете перенаправлены на Автор24
В этой статье мы расскажем вам, как найти периметр четырехугольника, зная его стороны, а также о том, какие бывают четырёхугольники.
Для удобства на страницу добавлен онлайн-калькулятор для расчёта периметра произвольного четырёхугольника.
Четырёхугольником называют геометрический объект, состоящий из четырёх вершин, три из которых не лежат на одной прямой, и четырёх отрезков.
Различают выпуклые и невыпуклые четырёхугольники. К выпуклым относят ромбы, трапеции, параллелограммы и некоторые другие фигуры.
Расчет периметра четырехугольника

Периметр любого четырёхугольника можно рассчитать путём суммирования его сторон:
$P = a + b + c + d$, где
$a, b, c, d$ — стороны четырёхугольника.
Рассмотрим, как использовать формулу для расчёта периметра четырехугольника.
Задача
Дан четырёхугольник со сторонами $a, b, c$ и $d$, равными соответственно $3, 4, 5$ и $6$ см. Найдите его периметр.
Решение:
Для получения ответа сложим все стороны:
$P = 3 + 4 + 5 + 6 = 18$ см.
Ответ совпадает с ответом онлайн-калькулятора, а значит, решение найдено верно.
Как найти периметр сторон четырехугольника, формула нахождения
Совсем недавно в России родители отправляли своих детей в первый класс и с нетерпением ждали их первых заданий. Они с удовольствием наблюдали за тем, как их дети знакомятся с буквами русского алфавита, учатся считать палочки и точечки, выводить различные кривые и прямые линии. Родители помогали знакомиться своим детям с тем, что тетрадь в клеточку предназначена для написания цифр, а тетрадь в линеечку — для письма.
Сегодня, будучи второклассниками, ученики России достигли больших успехов в сфере начального образования, а точнее, в математическом прогрессе. Учителя научили их складывать и вычитать, умножать, делить, измерять.
Кстати, по поводу измерения: с линейкой ребята вторых классов России уже знакомы, и применение ей, кроме как стрелять с задней парты в соседа бумажки, они тоже знают. Именно об измерениях мы и заведем сегодняшний разговор.
Как мы видим, прогресс обучения нынешних учеников проходит слегка в ускоренном режиме. С теми темами, например, такими как периметр, дети 90-х знакомились позже, а наши ребята узнают сегодня. Конечно, в этом нет ничего страшного. Время меняется, и программа обучения тоже должна не стоять на месте. Зато, как считают многие, наши дети будут умнее нас.
Школьное задание
Наверное, многих родителей сегодня удивляют нынешние задания для второклассников. В учебнике по математике для второго класса можно встретить такое задание, как, например: «Найди периметр четырехугольника, две стороны которого равны по 2 сантиметра, а другие две будут по 3 сантиметра». Как справиться с данным заданием?
Многие родители настоящего времени являются теми самыми детьми девяностых годов, и, естественно, в большинстве случаев, мало кто помнит, что такое периметр. Особенно, если учились не на отлично, да и не совсем на «хорошо».
Естественно, каждому родителю хотелось бы, чтоб его ребенку было проще в обучении, и они всеми силами стараются ему в этом помочь. Некоторым родителям сначала приходится справиться со своей душевной паникой, а уже потом продолжать объяснять своему ребенку. В этом случае многим помогает интернет, место, где можно найти ответы на все тревожные вопросы. Во времена девяностых, к сожалению, такой «роскоши» не было.
Вопросы:
- Что такое «периметр»?
- Как находить периметр четырехугольника?
Ответы на вопросы:
Для тех, кто знает, вспоминаем, а кто не знает — объясняем:
- Периметр — это сумма всех сторон четырехугольника. Всего лишь каждая грань по отдельности будет равна после сложения единому числу.
- Найти периметр, значит, что нужно взять линейку и измерить каждую границу четырехугольника. После выполнения данного действия необходимо сложить полученные числа между собой. Общая полученная сумма и будет являться периметром.
Решение:
В данном случае, по действиям нашей задачи, нам известны суммы сторон четырехугольника, а именно две из них по 2 сантиметра и две по 3 сантиметра. Поэтому нам остается всего лишь перечертить четырехугольник в тетрадь и сложить известные нам суммы каждой грани.
2+2+3+3=10
Как мы видим, периметр нашей четырехугольной фигуры равен 10.
В математике сумму всех сторон (периметр) мы обозначаем символом Р.
Теперь записываем правильное решение этой задачи:
Р=2+2+3+3;
Ответ: Р=10.
В математике существует формула, запомнив которую, вы никогда не будете забывать, как найти периметр (общую сумму всех сторон) четырехугольника и выглядит она так:
P = a + b + c + d (где a , b, c, d являются границами четырехугольника).
Кроме того, хотелось бы обратить внимание, что четырехугольник не обязательно будет являться прямоугольником. Это может быть и квадрат, у которого все стороны равны, и любая другая геометрическая фигура, у которой есть четыре стороны и такое же количество углов.
Грани произвольного четырехугольника могут совсем не совпадать ни с одной из сторон фигуры. Это могут быть совершенно разные числа. И, в итоге, получаются фигуры с четырьмя сторонами и теми же четырьмя углами. Фигура не будет похожа ни на квадрат, ни на прямоугольник, так как углы ее прямыми не будут. И периметр, соответственно мы вычисляем по той же самой единой формуле.
Или взять, например трапецию. Обычно у трапеции две стороны одинаковые, а другие две совсем не совпадают, но между собой параллельные.
На примере трапеция может выглядеть так: верхняя грань равна 2 сантиметра, левая и правая стороны по 3 сантиметра, соединяем их с нижней гранью и получаем трапецию. Высчитываем каждую ее сторону и снова получаем периметр четырехугольника.
Вычислить по формуле всегда будет проще, и не важно, каким числам равна каждая сторона.
Так как современные дети страны уже дошли до таблицы умножения, с периметром квадрата у них проблем не будет. Зная размер одной стороны квадрата, нужно умножить ее на все четыре равные стороны.
В общем, теперь стоит взять линейку с карандашом и лист бумаги. После этого следует начертить произвольные фигуры с четырьмя углами и высчитать общую сумму ее сторон.
Четырехугольники
теория по математике 📈 планиметрия
Четырехугольник – это геометрическая фигура, состоящая из четырех точек, никакие три из которых не лежат на одной прямой, и отрезков, последовательно соединяющих эти точки.
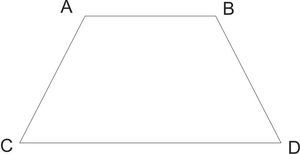
Выпуклый четырехугольник
Четырехугольник называется выпуклым, если он находится в одной полуплоскости (то есть все его стороны расположены только с одной стороны прямой, прямая НЕ разбивает фигуру) относительно прямой, содержащей любую его сторону. На рисунке показан выпуклый четырехугольник АВСD.
 Определение
Определение
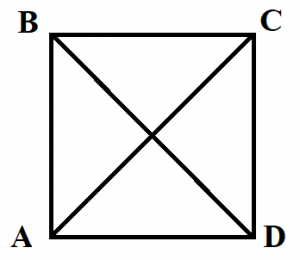
Диагональ четырехугольника – отрезок, соединяющий любые две не соседние вершины. На рисунке 2 диагоналями являются отрезки АС и BD.
Виды и свойства выпуклых четырехугольников
Сумма углов выпуклого четырехугольника равна 360 градусов.
Прямоугольник
Прямоугольник – это четырехугольник, у которого все углы прямые.
 На рисунке видно, что углы А, В, C и D прямые, то есть равны 90 градусов. Свойства прямоугольника, его периметр и площадь
На рисунке видно, что углы А, В, C и D прямые, то есть равны 90 градусов. Свойства прямоугольника, его периметр и площадь 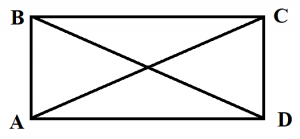
- Противоположные стороны прямоугольника равны (АВ=CD, ВС=АD).
- Диагонали прямоугольника равны (АС=ВD).
- Диагонали пересекаются и точкой пересечения делятся пополам.
- Периметр прямоугольника – это сумма длин всех сторон: Р=(а + b) × 2, где а и b соседние (смежные) стороны прямоугольника
- Площадь прямоугольника – это произведение длин соседних (смежных) сторон, формула для нахождения площади прямоугольника:
S=ab, где a и b соседние стороны прямоугольника.
Квадрат
Квадрат – это прямоугольник, у которого все стороны равны.
 Свойства квадрата
Свойства квадрата
- Диагонали квадрата равны (BD=AC).
- Диагонали квадрата пересекаются под углом 90 градусов.
- Диагонали квадрата точкой пересечения делятся пополам (BO=OD, AO=OC).
- Периметр квадрата – это сумма длин всех сторон. Так как все стороны квадрата равны, то его можно найти по формуле Р=4×а, где а — длина стороны квадрата.
- Площадь квадрата – это произведение длин соседних сторон, формула для нахождения площади прямоугольника S=a 2 , где a — длина стороны квадрата.
Параллелограмм
Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.

Ромб – это параллелограмм, у которого все стороны равны.

Трапеция
Трапеция – это четырехугольник, у которого только две противоположные стороны параллельны. Параллельные стороны называются основаниями трапеции, а две другие стороны – боковыми сторонами трапеции.

Виды трапеций
Трапеция называется прямоугольной, если у нее боковая сторона перпендикулярна основаниям. Прямоугольная трапеция имеет два прямых угла.

углы А и С равны по 90 градусов
Средняя линия трапеции
Сделаем чертеж параллелограмма и покажем на нем биссектрисы углов, которые пересекаются в точке N.

Угол ANB равен углу NАD как накрест лежащие при параллельных прямых ВС и АD и секущей AN. А по условию углы BАN и NАD равны (AN биссектриса). Следовательно, углы BАN и BNА равны. Значит, треугольник ABN является равнобедренным, у него АВ= BN.
Аналогично, через равенство углов CND, ADN и CDN доказывается, что треугольник CND является равнобедренным, у него CN=DC.
По условию задачи мы имеем параллелограмм, а по свойству параллелограмма – противолежащие стороны равны, т.е. АВ=СD, значит, АВ=BN=NC=CD. Таким образом, мы доказали, что BN=NC, т.е. N – середина ВС.
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите боковую сторону АВ трапеции ABCD, если углы АВС и BCD равны соответственно 30 0 и 135 0 , а СD =17
Сделаем чертеж, выполнив на нём дополнительные построения – высоты АМ и СН, которые равны как расстояния между параллельными сторонами трапеции.

Рассмотрим треугольник CНD, где CD=17, угол Н=90 0 , следовательно, треугольник прямоугольный. Найдем величину угла DCН, 135 0 – 90 0 =45 0 (так как провели высоту CН). Отсюда следует, что угол D=45 0 , так как треугольник прямоугольный. Значит, треугольник является равнобедренным (углы D и DCН равны по 45 градусов).
Найдем катеты CН и DН по теореме Пифагора, как катет равнобедренного треугольника по формуле с=а √ 2 , где с=17. Следовательно, CН = 17 √ 2 . . = 17 √ 2 2 . . .
Рассмотрим прямоугольный треугольник АВМ, где угол В равен 30 градусов, а катет АМ= CН= 17 √ 2 2 . . . Зная, что катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы, найдем АВ (она будет в два раза больше катета). АВ=2 × 17 √ 2 2 . . =17 √ 2
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
Основания трапеции равны 7 и 11, а высота равна 7. Найти площадь этой трапеции.

Для нахождения площади трапеции в справочном материале есть формула
S = a + b 2 . . h , для которой у нас известны и основания, и высота. Подставим в неё эти значения и вычислим: S = 7 + 11 2 . . ∙ 7 = 18 2 . . ∙ 7 = 9 ∙ 7 = 63
pазбирался: Даниил Романович | обсудить разбор | оценить
Радиус вписанной в квадрат окружности равен 22 √ 2 . Найти диагональ этого квадрата.

Для начала надо сделать построения на чертеже, чтобы увидеть, как располагаются известные и неизвестные элементы и чем они еще могут являться на чертеже.

Обозначим диагональ АВ, точкой О – центр окружности, С – один из углов квадрата. Покажем расстояние от центра окружности до стороны квадрата – радиус r. Если радиус равен 22 √ 2 , то сторона квадрата будет в два раза больше, т.е. 44 √ 2 .
Рассмотрим прямоугольный треугольник АВС, который является равнобедренным (так как по условию дан квадрат) и боковые стороны равны по 44 √ 2 . Нам надо найти диагональ, т.е. гипотенузу данного треугольника. Вспомним, что для нахождения гипотенузы равнобедренного треугольника есть формула с=а √ 2 , где с – гипотенуза, а – катет. Подставим в неё наши данные:
с=44 √ 2 × √ 2 =44 √ 4 =44 × 2=88
pазбирался: Даниил Романович | обсудить разбор | оценить
Площадь четырехугольника можно вычислить по формуле S= d 1 d 2 s i n a 2 . . , где d 1 и d 2 длины диагоналей четырехугольника, а – угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d 1 , если d 2 =16, sin a= 2 5 . . , a S=12,8
Для выполнения данного задания надо подставить все известные данные в формулу:
12,8= d 1 × 16 × 2 5 . . 2 . .
В правой части можно сократить 16 и 2 на 2: 12,8= d 1 × 8 × 2 5 . . 1 . .
Теперь умножим 8 на дробь 2 5 . . , получим 3,2: 12,8= d 1 × 3 , 2
Найдем неизвестный множитель, разделив 12,8 на 3,2: d 1 =12,8:3,2=4
pазбирался: Даниил Романович | обсудить разбор | оценить

На плане изображен дачный участок по адресу: п. Сосновка, ул. Зеленая, д. 19 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.
При входе на участок слева от ворот находится гараж. Справа от ворот находится сарай площадью 24 кв.м, а чуть подальше – жилой дом. Напротив жилого дома расположены яблоневые посадки. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, и огород с теплицей внутри (огород отмечен на плане цифрой 6). Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м. Между гаражом и сараем находится площадка, вымощенная такой же плиткой. К участку подведено электричество. Имеется магистральное газоснабжение.
Задание №1
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырех цифр без пробелов, запятых и других символов.
| Объекты | яблони | теплица | сарай | жилой дом |
| Цифры |
Решение
Для решения 1 задачи работаем с текстом и планом одновременно:
при входе на участок слева от ворот находится гараж (слева от входа находится объект под номером 2), итак, гараж — 2. Справа от ворот находится сарай площадью 24 кв.м (справа объект под номером 1), сарай – номер 1. А чуть подальше – жилой дом, следовательно, жилой дом – объект под номером 7. Напротив жилого дома расположены яблоневые посадки, на плане они обозначены цифрой 3. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, на плане видим, что к объекту под номером 4 ведет дорожка, значит баня – 4. Огород с теплицей внутри (огород отмечен на плане цифрой 6), в огороде расположена теплица – объект 5.
Итак, получили следующее:
1 – сарай; 2 – гараж; 3 – яблоневые посадки; 4 – баня; 5 – теплица; 6 – огород; 7 – жилой дом.
Заполняем нашу таблицу:
| Объекты | яблони | теплица | сарай | жилой дом |
| Цифры | 3 | 5 | 1 | 7 |
Записываем ответ: 3517
Задание №2
Плитки для садовых дорожек продаются в упаковках по 6 штук. Сколько упаковок плиток понадобилось, чтобы выложить все дорожки и площадку между сараем и гаражом?
Решение
Для начала надо определить, как обозначены дорожки, которые надо выложить плиткой, на плане. На плане они показаны серым цветом (мы их обведём голубым цветом).

Теперь ищем в условии задачи, что сказано про плитки и дорожки: «Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м».
Сосчитаем, сколько клеточек (плиток) на плане, получаем 65. Зная по условию задачи 1, что плитки продаются в упаковках по 6 штук, разделим 65 на 6. Заметим, что 65 на 6 не делится, получается приблизительно 10,8…Учитывая, что упаковки не делятся, округляем до большего целого числа, нам понадобится 11 упаковок.
Задание №3
Найдите расстояние от жилого дома до теплицы (расстояние между двумя ближайшими точками по прямой) в метрах.
Решение
Из задания 1 знаем, что жилой дом обозначен на плане цифрой 7, а теплица цифрой 5. Следовательно, на плане находим эти объекты и расстояние между двумя ближайшими точками по прямой (обозначим это голубым цветом). Видим, что это расстояние – 2 клетки. На плане показано, что длина стороны одной клетки равна 2 метра, значит, расстояние между двумя этими объектами равно 4 метра.

Задание №4
Найдите площадь, которую занимает гараж. Ответ дайте в квадратных метрах.
Решение
Найдем на плане гараж, это объект под номером 2. Гараж имеет прямоугольную форму, следовательно, нам надо найти площадь прямоугольника. Для этого надо найти длину и ширину. На плане показано, что длина стороны 1 клетки равна 2 метра, значит, длина гаража равна 8 м (4 клетки), а ширина — 6 м (3 клетки).

Зная ширину и длину, находим площадь гаража: 6х8=48 кв.м
Задание №5
Хозяин участка решил покрасить весь забор вокруг участка (только с внешней стороны) в зелёный цвет. Площадь забора равна 232 кв.м., а купить краску можно в одном из двух ближайших магазинов. Цена и характеристика краски и стоимость доставки заказа даны в таблице.
| Номер магазина | Расход краски | Масса краски в одной банке | Стоимость одной банки краски | Стоимость доставки заказа |
| 1 | 0,25 кг/кв.м | 6 кг | 3000 руб. | 500 руб. |
| 2 | 0,4 кг/кв.м | 5 кг | 1900 руб. | 800 руб. |
Во сколько рублей обойдется наиболее дешёвый вариант покупки с доставкой?
Решение
Определим, сколько килограммов краски понадобится для покраски забора площадью 232 кв.м:
1 магазин: 232х0,25=58 кг
2 магазин: 232х0,4=92,8 кг
Вычислим количество банок краски, которое надо купить, зная массу краски в 1 банке:
1 магазин: 58:6=9,7…; так как банки продаются целиком, то надо 10 банок (округляем до наибольшего целого числа)
2 магазин: 92,8:5=18,56; значит надо 19 банок.
Вычислим стоимость краски в каждом магазине плюс доставка:
1 магазин: 10х3000+500=30500 руб.
2 магазин: 19х1900+800=36900 руб.
Из решения задачи видно, что в 1 магазине купить краску выгоднее. Следовательно, наиболее дешёвый вариант покупки с доставкой будет стоить 30500 рублей.
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
[spoiler title=”источники:”]
http://liveposts.ru/articles/education-articles/matematika/kak-najti-perimetr-storon-chetyrehugolnika-formula-nahozhdeniya
[/spoiler]
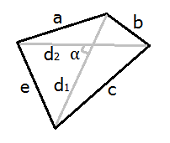
Четырехугольник – это многоугольник, у которого четыре вершины и четыре стороны. Четырехугольниками являются ромб, прямоугольник, квадрат, параллелограмм и трапеция.
Любой четырехугольник характеризуется сторонами и диагоналями d1 и d2 (см. рисунок). Также при решении задач может понадобиться угол α между диагоналями. Именно эти характеристики используются в формулах четырехугольника при вычислении площади и периметра.
Формула периметра четырехугольника
Периметр P четырехугольника можно получить, зная его стороны:
P = a + b + c + e
Формулы площади четырехугольника
Площадь четырехугольника S можно вычислить, зная его диагонали и угол α между ними:
S = 1/2 ⋅ d1 ⋅ d2 ⋅ sinα
Четырехугольник не является прямоугольником.
Периметр искать легко в отличие от площади. В периметре сложить величины всех сторон четырехугольника можно за несколько секунд, потому что стороны редко бывают больше 10 сантиметров, значит все подсчеты производим в уме.
Это четырехугольник.

Это формула периметра, обозначается буквой Р.

автор вопроса выбрал этот ответ лучшим
![]()
Tanyetta
[298K]
9 лет назад
Вспоминая уроки геометрии. Найти периметр четырехугольника очень просто! Для этого надо сложить длину всех его сторон. А если четырехугольник прямоугольный, то короткая сторона плюс длинная сторона умножить на 2! Удачных решений примеров и задач!
![]()
Носорог
[63.1K]
9 лет назад
Четырехугольник не всегда является прямоугольником или квадратом, все верно было сказано. И в то же время квадрат и прямоугольник можно назвать четырехугольниками. Четырехугольник может иметь как одинаковую длину сторон, так и разную. Ну а что такое периметр, периметр плоской фигуры (а в данном случае четырехугольник как раз плоская двухмерная фигура) – это сумма сторон. Так что чтобы узнать, вычислить периметр, необходимо знать длину каждой из сторон, а затем складываем длины и получаем конечную сумму.
У квадрата измеряем одну сторону и умножаем на 4. У квадрата же все стороны равны по длине. Это известно еще со школы с уроков геометрии.
![]()
Четырехугольник-это геометрическая фигура с четырьмя углами и с четырьмя сторонами. Так что найти периметр легко. Нужно измерить длину всех сторон и сложить их длины. И данный ответ и будит являться периметром.
![]()
ИнгаМус
[16.7K]
9 лет назад
Четырехугольник имеет четыре стороны, как мы видим уже из названия. Еще со школьных времен прочно запомнилась формула нахождения периметра четырехугольника.
Если он не является прямоугольником, то нам надо будет знать длину его каждой стороны по отдельности. Сложив их все вместе, мы и узнаем периметр этой фигуры.
Если кому – то потребуется вот здесь есть калькулятор расчета периметра четырехугольника.

elena-kh
[245K]
9 лет назад
Чтобы найти периметр, нужно сложить длины всех сторон. Если бы являлся прямоугольником, было бы проще, ведь можно было каждую длину умножить на 2, а потом сложить. У квадрата все еще проще – нужно длину одной стороны умножить на 4. У остальных прямоугольников, как правило, необходимо просто сложить все стороны. Хотя для параллелограммов тоже есть свои формулы.
![]()
Афанасий44
[442K]
9 лет назад
Четырёхугольник может быть неправильной формы и все стороны его могут иметь разную длину. Например, такие четырёхугольники:

В таких случаях, чтобы найти периметр неправильного четырёхугольника, надо просто измерить длину каждой его стороны и потом всё сложить.
![]()
Для того чтобы вам найти периметр четырёхугольника вам нужно вспомнить уроки геометрии в школе которые раньше для меня были очень интересными, так вот что надо сделать, надо сложить все длины четырёх сторон и у вас получится периметр.
![]()
Edvard
[10.5K]
9 лет назад
Найти периметр четырехугольника не представляет из себя ничего сложного. Надо всего лишь найти сумму длин всех четырех сторон четырехугольника. Этот нехитрый способ известен нам еще со школьной скамьи.
![]()
Безразличный
[256K]
10 лет назад
Сложите длины всех четырех сторон и получите периметр.
![]()
Агафья
[118K]
8 лет назад
Вообще просто для этого достаточно перемерить все стороны прямоугольника и их величины сложить вместе. Вот эта сумма и будет являться периметром неправильного четырёхугольника. Меня этому ещё в школе научили.
Знаете ответ?
 В этой статье мы рассмотрим все основные свойства и признаки четырехугольника.
В этой статье мы рассмотрим все основные свойства и признаки четырехугольника.
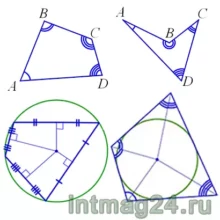
Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три точки не лежат на одной прямой.
Четырехугольники бывают выпуклые, если они расположены в одной полуплоскости относительно прямой, которая содержит одну из его сторон (ABCD) и невыпуклые (A1B1C1D1).
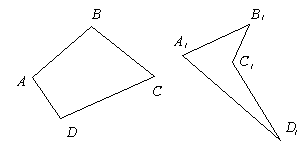
Если любые две противолежащие точки выпуклого четырёхугольника соединить между собой отрезком, то весь отрезок будет лежать внутри многоугольника. Для невыпуклого четырёхугольника это не выполняется (рисунок ниже).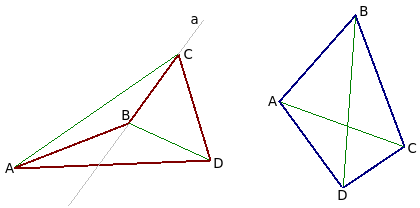
Диагонали выпуклого четырёхугольника лежат внутри него и пересекаются. Одна из диагоналей невыпуклого четырёхугольника лежит снаружи, а другая внутри него, и эти диагонали не пересекаются.
Определения для четырехугольника
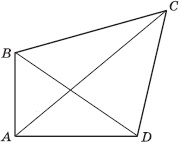 Данный четырёхугольник обозначается ABCD.
Данный четырёхугольник обозначается ABCD.- Точки A, B, C, D называются его вершинами, а отрезки AB, BC, CD, DA – его сторонами.
- Смежные стороны – соседние стороны, имеющие общую вершину. Пары смежных сторон: AB и AD, AB и BC, BC и CD, CD и AD.
- Противолежащие стороны – несмежные стороны, не имеющие общих вершин. Пары противолежащих сторон: AB и CD, BC и AD.
Диагонали четырехугольника – отрезки, соединяющие противолежащие вершины. AC и BD – диагонали четырехугольника ABCD.
Виды четырехугольников:
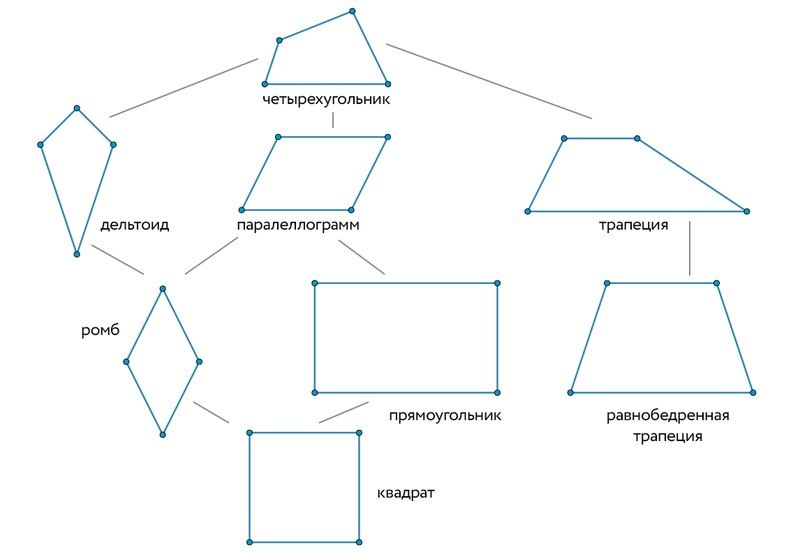
Если рассмотреть схему, то каждый следующий четырехугольник обладает всеми свойствами предыдущего. Поэтому запоминать надо совсем немного.
Трапеция — это четырехугольник, у которого две противолежащие стороны параллельны, а две другие не параллельны. Трапеции бывают: произвольная, равносторонняя, прямоугольная.
Параллелограмм — это четырехугольник у которого противолежащие стороны параллельны. В параллелограмме:
— противоположные стороны и противоположные углы равны.
— диагонали параллелограмма делятся точкой пересечения пополам.
Соответственно, если четырехугольник обладает этими свойствами, то он является параллелограммом.
Прямоугольник — это параллелограмм, у которого все углы прямые. Прямоугольник является частным случаем параллелограмма, поэтому обладает всеми его свойствами.
Ромб — это параллелограмм, у которого все стороны равны. Ромб является частным случаем параллелограмма, поэтому обладает всеми его свойствами. В ромбе:
— противоположные углы равны,
— диагонали точкой пересечения делятся пополам,
— диагонали взаимно перпендикулярны,
— диагонали ромба являются биссектрисами углов.
Квадрат — это прямоугольник, у которого все стороны равны. Квадрат является частным случаем прямоугольника и частным случаем ромба, поэтому обладает всеми их свойствами. В квадрате:
— все углы равны 90 градусов,
— диагонали точкой пересечения делятся пополам,
— диагонали взаимно перпендикулярны,
— диагонали являются биссектрисами углов,
— диагонали равны.
Свойства углов четырехугольника
- Сумма углов четырёхугольника равна 360°
- Сумма внешних углов четырехугольника, взятых по одному при каждой вершине, равна 360°.
- Не существует четырёхугольников, у которых все углы острые или все углы тупые.
- Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов.
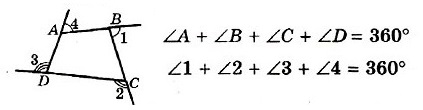
Свойства сторон четырехугольника
- Каждая сторона четырехугольника меньше суммы всех его других сторон.
- Сумма диагоналей меньше его периметра.
Четырехугольник и окружность
Четырехугольник вокруг окружности.
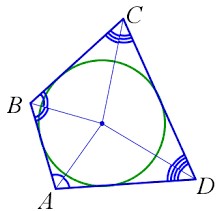
- Четырехугольник называется описанным, если существует окружность, касающаяся всех его сторон.
- В четырёхугольник можно вписать окружность, если суммы его противолежащих сторон равны (AB+CD=AD+BC).
- Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.
Четырехугольник внутри окружности.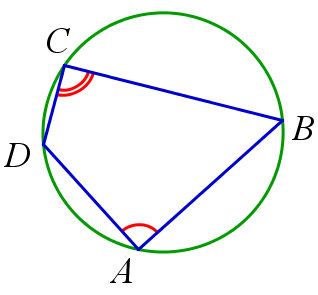
- Вписанный четырёхугольник — это четырёхугольник, все вершины которого лежат на одной окружности. Эта окружность называется описанной.
- Вокруг четырёхугольника можно описать окружность, если сумма двух его противоположных углов равна 180°.
- Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.
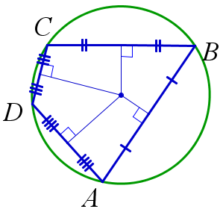
- Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон (AC*BD=AB*CD+AD*BC).
Частные случаи:
- Параллелограмм, вписанный в окружность – это прямоугольник, центр окружности совпадает с точкой пересечения диагоналей.
- Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.
- Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной.
Диагонали четырехугольника
- Диагонали выпуклого четырёхугольника пересекаются в одной точке.
- Две противоположные стороны четырёхугольника перпендикулярны тогда и только тогда, когда сумма квадратов двух других противоположных сторон равна сумме квадратов диагоналей.
- Диагонали четырёхугольника перпендикулярны тогда и только тогда, когда суммы квадратов противоположных сторон равны.
Периметр и площадь четырехугольника
Периметр четырёхугольника равен сумме длин всех его сторон: ![]() где a, b, c, d – длины сторон четырёхугольника.
где a, b, c, d – длины сторон четырёхугольника.
Площадь произвольного выпуклого четырёхугольника можно найти по формуле: ![]() где d1 и d2— диагонали четырёхугольника, a — угол между диагоналями.
где d1 и d2— диагонали четырёхугольника, a — угол между диагоналями.
Площадь вписанного четырёхугольника может быть вычислена по формуле: 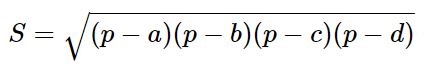 где a, b, c, d – длины сторон четырёхугольника, p=(a+b+c+d)/2 – его полупериметр.
где a, b, c, d – длины сторон четырёхугольника, p=(a+b+c+d)/2 – его полупериметр.
Площадь описанного четырёхугольника равна произведению его полупериметра на радиус вписанной окружности: ![]()

формулы и примеры заданий для второго класса
Совсем недавно в России родители отправляли своих детей в первый класс и с нетерпением ждали их первых заданий. Они с удовольствием наблюдали за тем, как их дети знакомятся с буквами русского алфавита, учатся считать палочки и точечки, выводить различные кривые и прямые линии. Родители помогали знакомиться своим детям с тем, что тетрадь в клеточку предназначена для написания цифр, а тетрадь в линеечку — для письма.
Сегодня, будучи второклассниками, ученики России достигли больших успехов в сфере начального образования, а точнее, в математическом прогрессе. Учителя научили их складывать и вычитать, умножать, делить, измерять.
Кстати, по поводу измерения: с линейкой ребята вторых классов России уже знакомы, и применение ей, кроме как стрелять с задней парты в соседа бумажки, они тоже знают. Именно об измерениях мы и заведем сегодняшний разговор.
Как мы видим, прогресс обучения нынешних учеников проходит слегка в ускоренном режиме.
С теми темами, например, такими как периметр, дети 90-х знакомились позже, а наши ребята узнают сегодня. Конечно, в этом нет ничего страшного. Время меняется, и программа обучения тоже должна не стоять на месте. Зато, как считают многие, наши дети будут умнее нас.
Содержание:
- Школьное задание
Наверное, многих родителей сегодня удивляют нынешние задания для второклассников. В учебнике по математике для второго класса можно встретить такое задание, как, например: «Найди периметр четырехугольника, две стороны которого равны по 2 сантиметра, а другие две будут по 3 сантиметра». Как справиться с данным заданием?
Многие родители настоящего времени являются теми самыми детьми девяностых годов, и, естественно, в большинстве случаев, мало кто помнит, что такое периметр. Особенно, если учились не на отлично, да и не совсем на «хорошо».
Естественно, каждому родителю хотелось бы, чтоб его ребенку было проще в обучении, и они всеми силами стараются ему в этом помочь.
Некоторым родителям сначала приходится справиться со своей душевной паникой, а уже потом продолжать объяснять своему ребенку. В этом случае многим помогает интернет, место, где можно найти ответы на все тревожные вопросы. Во времена девяностых, к сожалению, такой «роскоши» не было.
Вопросы:
- Что такое «периметр»?
- Как находить периметр четырехугольника?
Ответы на вопросы:
Для тех, кто знает, вспоминаем, а кто не знает — объясняем:
- Периметр — это сумма всех сторон четырехугольника. Всего лишь каждая грань по отдельности будет равна после сложения единому числу.
- Найти периметр, значит, что нужно взять линейку и измерить каждую границу четырехугольника. После выполнения данного действия необходимо сложить полученные числа между собой. Общая полученная сумма и будет являться периметром.
Решение:
В данном случае, по действиям нашей задачи, нам известны суммы сторон четырехугольника, а именно две из них по 2 сантиметра и две по 3 сантиметра. Поэтому нам остается всего лишь перечертить четырехугольник в тетрадь и сложить известные нам суммы каждой грани.
Поэтому нам остается всего лишь перечертить четырехугольник в тетрадь и сложить известные нам суммы каждой грани.
2+2+3+3=10
Как мы видим, периметр нашей четырехугольной фигуры равен 10.
В математике сумму всех сторон (периметр) мы обозначаем символом Р.
Теперь записываем правильное решение этой задачи:
Р=2+2+3+3;
Ответ: Р=10.
В математике существует формула, запомнив которую, вы никогда не будете забывать, как найти периметр (общую сумму всех сторон) четырехугольника и выглядит она так:
P = a + b + c + d
(где a , b, c, d являются границами четырехугольника).
Кроме того, хотелось бы обратить внимание, что четырехугольник не обязательно будет являться прямоугольником. Это может быть и квадрат, у которого все стороны равны, и любая другая геометрическая фигура, у которой есть четыре стороны и такое же количество углов.
Грани произвольного четырехугольника могут совсем не совпадать ни с одной из сторон фигуры. Это могут быть совершенно разные числа. И, в итоге, получаются фигуры с четырьмя сторонами и теми же четырьмя углами. Фигура не будет похожа ни на квадрат, ни на прямоугольник, так как углы ее прямыми не будут. И периметр, соответственно мы вычисляем по той же самой единой формуле.
Или взять, например трапецию. Обычно у трапеции две стороны одинаковые, а другие две совсем не совпадают, но между собой параллельные.
На примере трапеция может выглядеть так: верхняя грань равна 2 сантиметра, левая и правая стороны по 3 сантиметра, соединяем их с нижней гранью и получаем трапецию. Высчитываем каждую ее сторону и снова получаем периметр четырехугольника.
Вычислить по формуле всегда будет проще, и не важно, каким числам равна каждая сторона.
Так как современные дети страны уже дошли до таблицы умножения, с периметром квадрата у них проблем не будет. Зная размер одной стороны квадрата, нужно умножить ее на все четыре равные стороны.
В общем, теперь стоит взять линейку с карандашом и лист бумаги. После этого следует начертить произвольные фигуры с четырьмя углами и высчитать общую сумму ее сторон.
Как найти периметр? — Занимательная математика — Математика
- 27 ноября 2020 года
- Теги: квадрат, треугольник, периметр, прямоугольник
Комментариев: 0
Периметр — это расстояние вокруг фигуры.
В реальной жизни периметр — это забор вокруг двора или рамка вокруг картины. Периметр образует двухмерную форму.
Как найти периметр четырехугольника
Чтобы найти периметр четырехугольника, сложите размеры четырех сторон фигуры. Формула: a+b+c+d=P
Четырехугольник — это многоугольник, имеющий четыре стороны и четыре угла. Наиболее распространенные типы четырехугольников — квадрат, прямоугольник, ромб, трапеция и параллелограмм.
Как найти периметр квадрата и ромба
У квадрата и ромба по четыре равные стороны, но у квадрата четыре прямых угла. Формула периметра одинакова для обеих фигур, и вам нужно знать только размер одной стороны. Формула: 4*a = P, P-периметр, s — длина одной стороны. Если размер одной стороны составляет 2 сантиметра, умножьте 2 на 4. Периметр равен 8 сантиметрам.
Формула периметра одинакова для обеих фигур, и вам нужно знать только размер одной стороны. Формула: 4*a = P, P-периметр, s — длина одной стороны. Если размер одной стороны составляет 2 сантиметра, умножьте 2 на 4. Периметр равен 8 сантиметрам.
Как найти периметр прямоугольника и параллелограмма
Формулы для периметра прямоугольника и параллелограмма одинаковы, потому что каждый многоугольник имеет два набора равных сторон. Формула 2*(a + b) = P, где a обозначает длину, а b обозначает ширину. Рассмотрим прямоугольник длиной 2 сантиметра и шириной 4 сантиметра. Сумма длины и ширины равна 6. Умножьте 6 на 2, и вы получите периметр в 12 сантиметров.
Как найти периметр трапеции
Формула для трапеции немного отличается, потому что трапеция — это четырехугольник, у которого есть две параллельные стороны неравной длины. Две стороны имеют одинаковую длину. Две другие стороны имеют равную длину друг друга, но длина этих двух сторон отличается от длины двух других сторон.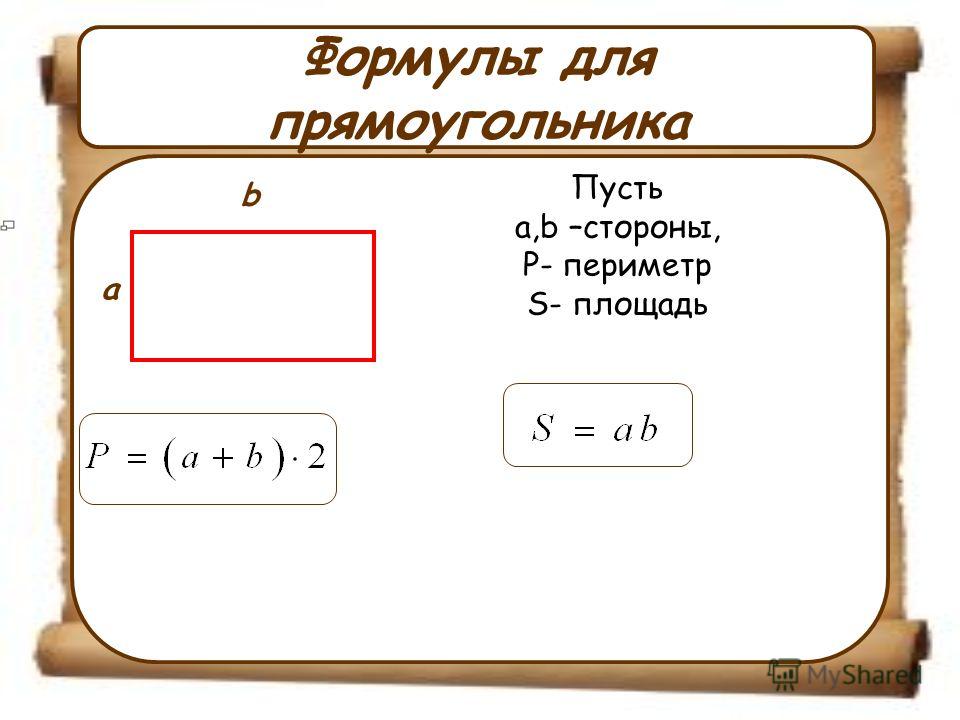 Некоторые парты в классах имеют форму трапеции. Формула: a + b + c + d = P. Каждая буква соответствует разной стороне или основанию фигуры. Например, предположим, что трапеция имеет размеры 2, 3, 2 и 5 сантиметров. Периметр равен 2 + 3 + 2 + 5, что составляет 12 сантиметров.
Некоторые парты в классах имеют форму трапеции. Формула: a + b + c + d = P. Каждая буква соответствует разной стороне или основанию фигуры. Например, предположим, что трапеция имеет размеры 2, 3, 2 и 5 сантиметров. Периметр равен 2 + 3 + 2 + 5, что составляет 12 сантиметров.
Как найти периметр неправильного четырехугольника
Формула неправильного четырехугольника — многоугольника с четырьмя сторонами разной длины — такая же, как у трапеции. Формула: a + b + c + d = P. Например, предположим, что четырехугольник имеет стороны длиной 1, 5, 3 и 4 см. Периметр равен 1 + 5 + 3 + 4 или 13 см.
Использование координат для определения длины стороны
Если вам известны только координаты фигуры, найдите размеры сторон, определив расстояние между точками. Например, найдите расстояние между точками A и B для одной стороны и расстояние между точками B и C для другой стороны. Затем подставьте боковые размеры в соответствующую формулу, чтобы определить периметр.
Периметр четырехугольника – определение, формула и примеры
Периметр четырехугольника – это общая длина его границы. Четырехугольник — это четырехугольник, который может быть правильным или неправильным. В правильном четырехугольнике все стороны равны по длине и все углы равны, тогда как в неправильном четырехугольнике стороны и углы не равны. Существует 6 конкретных типов четырехугольников — квадрат, прямоугольник, параллелограмм, ромб, воздушный змей и трапеция. Давайте узнаем, как найти периметр четырехугольника на этой странице.
| 1. | Что такое периметр четырехугольника? |
| 2. | Периметр четырехугольника Формула |
| 3. | Формулы периметра четырехугольников различных типов |
| 4. | Периметр четырехугольника с вписанной окружностью |
| 5. | Часто задаваемые вопросы о периметре четырехугольника |
Что такое периметр четырехугольника?
Периметр четырехугольника — это длина его границы, т. е. если мы соединим все четыре стороны четырехугольника, чтобы сформировать один отрезок, длина полученного отрезка называется его периметром. Таким образом, единица измерения периметра четырехугольника такая же, как и у его стороны, т. е. измеряется в линейных единицах, таких как метры, дюймы, сантиметры и т. д.
е. если мы соединим все четыре стороны четырехугольника, чтобы сформировать один отрезок, длина полученного отрезка называется его периметром. Таким образом, единица измерения периметра четырехугольника такая же, как и у его стороны, т. е. измеряется в линейных единицах, таких как метры, дюймы, сантиметры и т. д.
Периметр четырехугольника Формула
Мы знаем, что периметр четырехугольника можно получить, сложив длины всех его сторон. Это можно выразить простой формулой. Например, формула для периметра четырехугольника ABCD может быть выражена как
Периметр = AB + BC + CD + DA
Формулы периметра четырехугольников различных типов
Мы уже видели, что существует 6 конкретных типов четырехугольников: квадрат, прямоугольник, параллелограмм, ромб, воздушный змей и трапеция. Хотя периметр четырехугольника представляет собой сумму всех его сторон, иногда не все длины сторон могут быть заданы. В таких случаях нам нужно вспомнить свойства четырехугольников относительно сторон, чтобы получить длины сторон, которые не даны. Например, если нам нужно найти периметр квадрата с заданной длиной только одной стороны, нам нужно вспомнить одно из свойств квадрата, что все его стороны равны. Итак, если мы предположим, что одна сторона квадрата равна х, его периметр будет х + х + х + х = 4х. Таким же образом мы можем вывести формулы периметра всех 6 конкретных типов четырехугольников. Обратите внимание на следующий рисунок, чтобы увидеть различные формулы, используемые для вычисления периметра четырехугольника.
Например, если нам нужно найти периметр квадрата с заданной длиной только одной стороны, нам нужно вспомнить одно из свойств квадрата, что все его стороны равны. Итак, если мы предположим, что одна сторона квадрата равна х, его периметр будет х + х + х + х = 4х. Таким же образом мы можем вывести формулы периметра всех 6 конкретных типов четырехугольников. Обратите внимание на следующий рисунок, чтобы увидеть различные формулы, используемые для вычисления периметра четырехугольника.
Периметр четырехугольника с вписанной окружностью
Иногда внутри четырехугольника находится окружность. Это называется описанным четырехугольником или четырехугольником с вписанной окружностью. В таких случаях мы используем свойство касательной окружности, которое гласит: «любые две касательные, проведенные к окружности из точки, имеют одинаковую длину». Мы увидим, как найти периметр описанного четырехугольника (или) периметр четырехугольника с окружностью внутри него на приведенном ниже примере.
Пример: Найдите периметр следующего четырехугольника.
Решение:
Используя свойство касательных «Любые две касательные, проведенные к окружности из точки, имеют одинаковую длину», найдем периметр четырехугольника с вписанной окружностью.
PT = PU = 5 дюймов
QV = QU = 2 дюйма
RW = RV = 3 дюйма
ST = SW = 4 дюйма
Теперь периметр четырехугольника равен
PQ + QR + RS + SP
= (PU + UQ) + (QV + VR) + (RW + WS) + (ST + TP)
= (5 + 2) + (2 + 3) + (3 + 4) + (4 + 5)
= 28 дюймов
Следовательно, периметр данного четырехугольника = 28 дюймов.
Примечание: Мы можем использовать то же свойство касательных окружности «две касательные, проведенные к окружности из точки, имеют одинаковую длину», чтобы найти периметр вписанного в окружность четырехугольника (четырехугольник, вписанный в окружность) также.
Решенные примеры на периметре четырехугольника
-
Пример 1: Найдите периметр воздушного змея, смежные стороны которого равны 7 единицам и 13 единицам.

Решение:
Мы знаем, что у воздушного змея две пары равных смежных сторон. Итак, используя формулу периметра четырехугольника, мы сложим стороны воздушного змея. Стороны данного воздушного змея составляют 7 единиц, 7 единиц, 13 единиц и 13 единиц.
Таким образом, периметр данного воздушного змея равен
7 + 7 + 13 + 13 = 40 единиц.
Ответ: Периметр данного воздушного змея = 40 единиц.
-
Пример 2: Найдите периметр трапеции, стороны которой равны 4, 6, 7 и 9 единицам.
Решение:
Мы знаем, что периметр четырехугольника можно получить, сложив все его стороны. В случае трапеции периметр можно рассчитать по формуле P = a + b + c + d.
Подставляя значения в формулу, Периметр трапеции = 4 + 6 + 7 + 9 = 26 единиц.
Ответ: Периметр данной трапеции равен 26 единицам.
перейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила.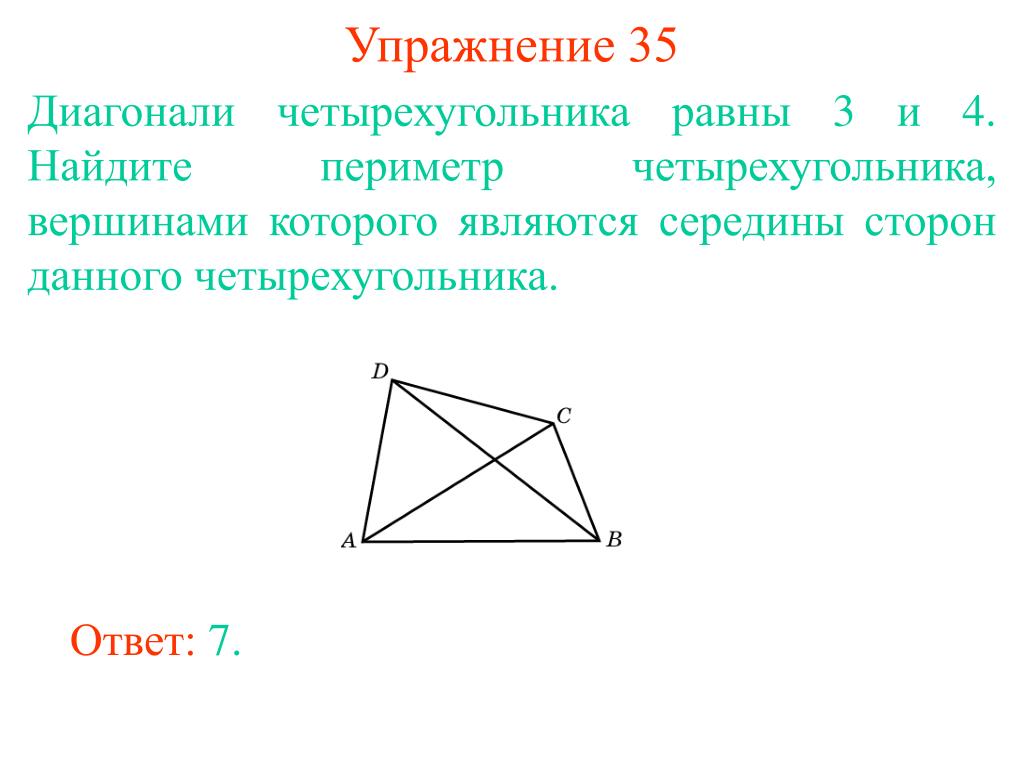 Узнайте, почему математика стоит за нашими сертифицированными экспертами Cuemath.
Узнайте, почему математика стоит за нашими сертифицированными экспертами Cuemath.
Записаться на бесплатный пробный урок
Практические вопросы по периметру четырехугольника
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о периметре четырехугольника
Что означает периметр четырехугольника?
Периметр четырехугольника равен общей длине его границы. Например, периметр четырехугольника ABCD можно выразить как Периметр = AB + BC + CD + DA. Это означает, что если известны все стороны четырехугольника, мы можем получить его периметр, сложив все его стороны.
Какая формула периметра четырехугольника?
Основная формула, которая используется для нахождения периметра четырехугольника: Периметр = a + b + c + d, где a, b, c и d — четыре стороны четырехугольника. Хотя эта формула используется для всех четырехугольников, для некоторых четырехугольников, таких как квадрат и прямоугольник, эту формулу можно упростить, потому что в квадрате все стороны равны, поэтому формула периметра принимает вид a + a + a + a = 4a.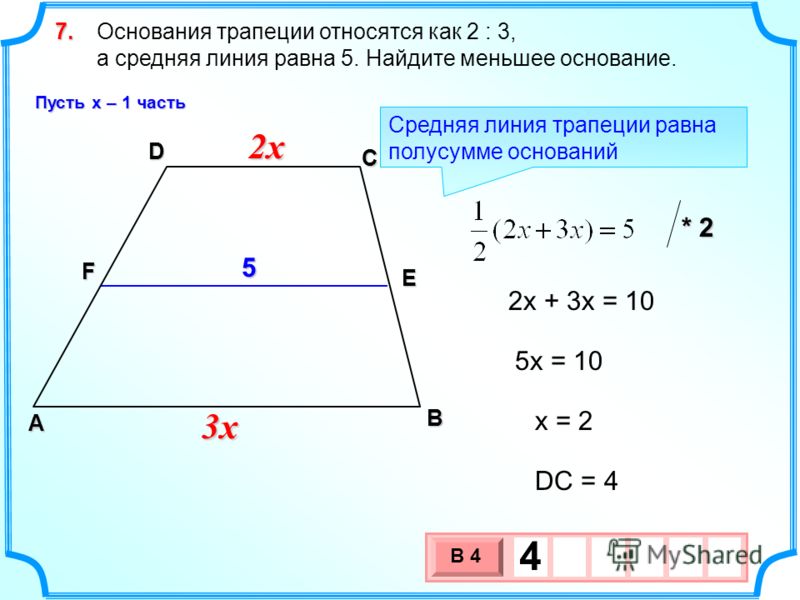 Точно так же в прямоугольнике противоположные стороны равны, поэтому формула меняется на 2 (длина + ширина). Однако основная формула для периметра всех четырехугольников остается неизменной.
Точно так же в прямоугольнике противоположные стороны равны, поэтому формула меняется на 2 (длина + ширина). Однако основная формула для периметра всех четырехугольников остается неизменной.
Как найти периметр четырехугольника с отсутствующей стороной?
Недостающую сторону четырехугольника можно найти, используя свойства четырехугольников. Как только все недостающие стороны найдены, мы можем найти периметр четырехугольника, сложив все длины сторон. Например, если мы знаем одну сторону квадрата, мы можем найти остальные 3 стороны, потому что мы знаем, что все стороны квадрата равны. После этого можем найти периметр.
Как найти периметр четырехугольника с вписанной окружностью?
Когда четырехугольник имеет вписанную окружность, стороны четырехугольника становятся касательными к окружности. Следовательно, свойство касательных можно использовать для нахождения периметра данного четырехугольника. Свойство касательной гласит: «Любые две касательные, проведенные из точки в некоторые точки окружности, всегда имеют одинаковую длину». Это свойство помогает найти недостающие длины сторон четырехугольника. Как только все недостающие стороны найдены, мы можем найти периметр четырехугольника, сложив все четыре стороны.
Это свойство помогает найти недостающие длины сторон четырехугольника. Как только все недостающие стороны найдены, мы можем найти периметр четырехугольника, сложив все четыре стороны.
Как найти периметр четырехугольника с координатами?
Когда известны координаты вершин четырехугольника, мы сначала находим длины его сторон, используя формулу расстояния. Затем мы складываем все четыре стороны, чтобы найти его периметр.
Как найти периметр четырехугольника на графике?
Чтобы найти периметр четырехугольника на графике, мы используем следующие шаги.
- Шаг 1: Найдите координаты вершин на графике.
- Шаг 2: Примените формулу расстояния, чтобы найти длины сторон четырехугольника.
- Шаг 3: Сложите все длины сторон, и сумма даст периметр четырехугольника.
Как найти периметр четырехугольника, вписанного в окружность?
Когда четырехугольник вписан в окружность, он называется вписанным четырехугольником.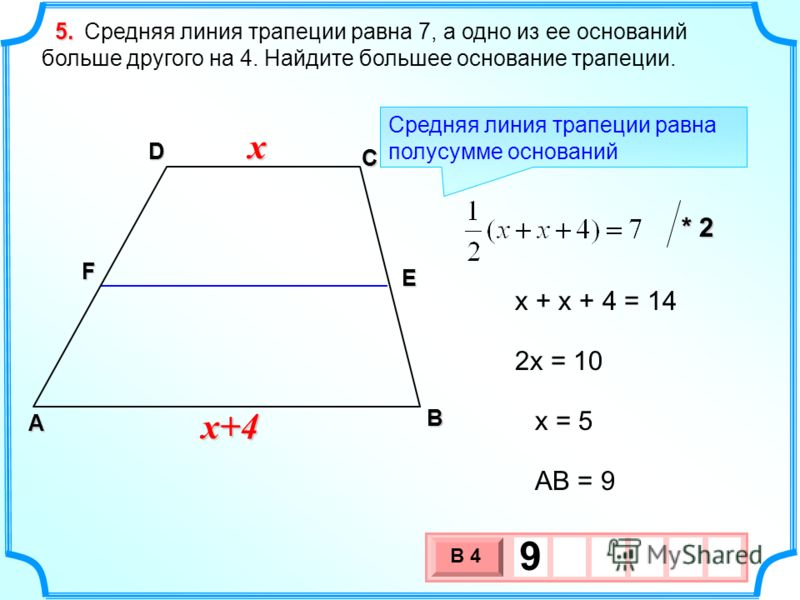 Чтобы найти недостающие стороны вписанного четырехугольника, мы применяем свойство касательной к окружности, которое гласит: «Любые две касательные к окружности, проведенные из одной точки, имеют одинаковую длину». Найдя недостающие стороны, мы складываем все четыре стороны, чтобы найти периметр.
Чтобы найти недостающие стороны вписанного четырехугольника, мы применяем свойство касательной к окружности, которое гласит: «Любые две касательные к окружности, проведенные из одной точки, имеют одинаковую длину». Найдя недостающие стороны, мы складываем все четыре стороны, чтобы найти периметр.
Как вычислить периметр четырехугольника
Обновлено 13 марта 2018 г.
Автор: Tabitha Burgtorf
Чтобы вычислить периметр четырехугольника, сложите измерения четырех сторон. Периметр — это расстояние вокруг фигуры. В реальных приложениях периметром является забор вокруг двора или рамка вокруг картины. Периметр простирается по всему периметру двумерной формы. Четырехугольник — это многоугольник , имеющий четыре стороны и четыре угла. К наиболее распространенным типам четырехугольников относятся квадрат, прямоугольник, ромб, трапеция и параллелограмм.
Периметр квадрата и ромба
У квадрата и ромба по четыре равные стороны, а у квадрата четыре прямых угла.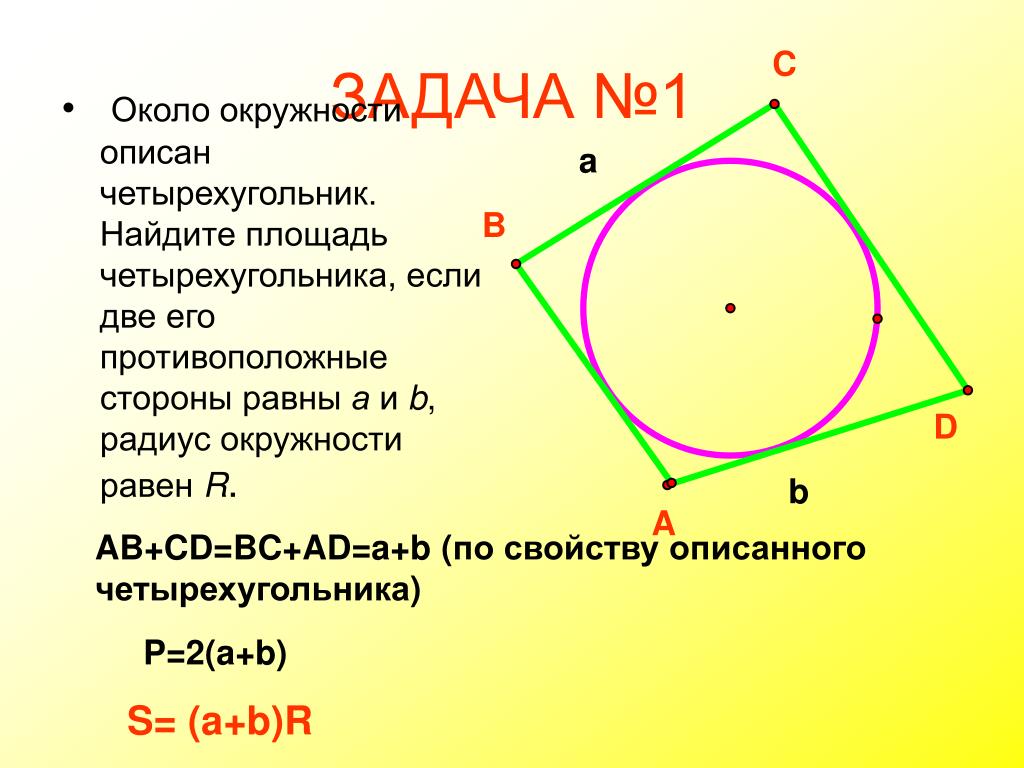 Формула периметра одинакова для обеих фигур, и вам нужно знать измерение только одной стороны. Формула: 4 x s = периметр, , где s представляет собой длину одной стороны. Если размер одной стороны составляет 2 дюйма, умножить 2 на 4. Периметр 8 дюймов.
Формула периметра одинакова для обеих фигур, и вам нужно знать измерение только одной стороны. Формула: 4 x s = периметр, , где s представляет собой длину одной стороны. Если размер одной стороны составляет 2 дюйма, умножить 2 на 4. Периметр 8 дюймов.
Периметр прямоугольника и параллелограмма
Формулы для периметра прямоугольника и параллелограмма одинаковы, потому что каждый многоугольник имеет два набора равных сторон. Формула: 2 (l + w) = периметр, , где l представляет длину, а w представляет ширину. Рассмотрим прямоугольник, длина которого 2 дюйма, а ширина 4 дюйма. Сумма длины и ширины равна 6. Умножьте 6 на 2, и вы получите периметр 12 дюймов.
Периметр трапеции
Формула для трапеции немного отличается, потому что трапеция — это четырехугольник, у которого две параллельные стороны неравной длины.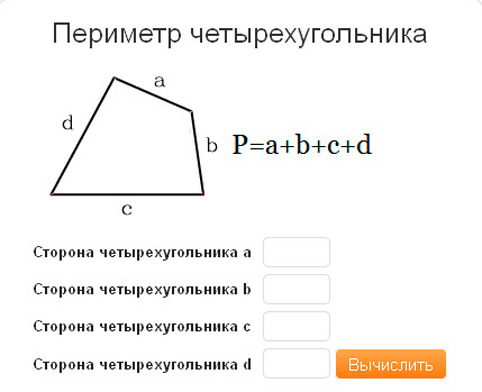 Две стороны имеют равные длины друг к другу. Две другие стороны имеют одинаковую длину по отношению друг к другу, но длина этих двух сторон отличается от длины двух других сторон. Некоторые школьные парты в классах имеют форму трапеции.
Две стороны имеют равные длины друг к другу. Две другие стороны имеют одинаковую длину по отношению друг к другу, но длина этих двух сторон отличается от длины двух других сторон. Некоторые школьные парты в классах имеют форму трапеции.
Формула a + b + c + d = периметр. Каждая буква соответствует разной стороне или основанию фигуры. Например, предположим, что размеры ребер трапеции равны 2, 3, 2 и 5 дюймам. Периметр равен 2 + 3 + 2 + 5, что равно 12 дюймам.
Периметр неправильного четырехугольника
Формула неправильного четырехугольника — многоугольника с четырьмя сторонами разной длины — такая же, как и у трапеции. Формула a + b + c+ d = периметр. Например, предположим, что четырехугольник имеет длины сторон 1, 5, 3 и 4 дюйма. Периметр равен 1 + 5 + 3 + 4 или 13 дюймов.
Использование координат для определения длины стороны
Если вы знаете только координаты фигуры, найдите размеры сторон, найдя расстояние между точками.