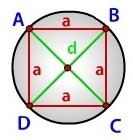
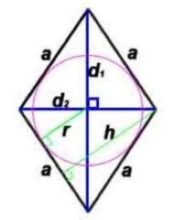
Как найти периметр вписанной окружности в ромбе

Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!

Контакты

Администратор, решение задач
Роман

Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym

Решение задач
Андрей

facebook:
dniprovets25

Нахождение радиуса вписанной в ромб окружности

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, вписанной в ромб. Также разберем примеры решения задач для закрепления изложенного материала.

Формулы вычисления радиуса вписанной в ромб окружности

Через диагонали и сторону

Радиус r вписанной в ромб окружности равняется произведению его диагоналей, деленному на сторону, умноженную на 4.

d₁ и d₂ – диагонали ромба;
a – сторона ромба.

Через диагонали

Радиус r вписанной в ромб окружности можно найти, зная только длины его обеих диагоналей:

Эту формулу можно получить, если сторону a в формуле выше выразить через диагонали (согласно одному из свойств ромба):

Через сторону и угол

Радиус окружности r, вписанной в ромб, равняется половине произведения его стороны и синуса любого угла.

Через высоту

Радиус вписанного в ромб круга равняется половине его высоты.

Примеры задач

Задание 1
Известно, что диагонали ромба равны 6 и 8 см. Найдите радиус окружности, вписанной в него.

Решение
Применим соответствующую формулу, подставив в нее известные значения:

Задание 2
Вычислите радиус вписанного в ромб круга, если его сторона равна 11 см, а один из углов – 30°.

Решение
В данном случае мы можем воспользоваться последней из рассмотренных выше формул:

Ромб. Формулы, признаки и свойства ромба

Признаки ромба

∠BAC = ∠CAD или ∠BDA = ∠BDC

Δ ABO = Δ BCO = Δ CDO = Δ ADO

Основные свойства ромба

∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC

AC 2 + BD 2 = 4AB 2

Сторона ромба

Формулы определения длины стороны ромба:

1. Формула стороны ромба через площадь и высоту:

2. Формула стороны ромба через площадь и синус угла:

3. Формула стороны ромба через площадь и радиус вписанной окружности:

4. Формула стороны ромба через две диагонали:

5. Формула стороны ромба через диагональ и косинус острого угла ( cos α ) или косинус тупого угла ( cos β ):

6. Формула стороны ромба через большую диагональ и половинный угол:

7. Формула стороны ромба через малую диагональ и половинный угол:

8. Формула стороны ромба через периметр:

Диагонали ромба

Формулы определения длины диагонали ромба:

d ₁ = a √ 2 + 2 · cosα

d ₁ = a √ 2 – 2 · cosβ

d ₂ = a √ 2 + 2 · cosβ

d ₂ = a √ 2 – 2 · cosα

d ₁ = 2 a · cos ( α /2)

d ₁ = 2 a · sin ( β /2)

d ₂ = 2 a · sin ( α /2)

d ₂ = 2 a · cos ( β /2)

7. Формулы диагоналей через площадь и другую диагональ:

8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:

Периметр ромба

Периметром ромба называется сумма длин всех сторон ромба.

Длину стороны ромба можно найти за формулами указанными выше.

Формула определения длины периметра ромба:

Площадь ромба

Формулы определения площади ромба:

4. Формула площади ромба через две диагонали:

5. Формула площади ромба через синус угла и радиус вписанной окружности:

6. Формулы площади через большую диагональ и тангенс острого угла ( tgα ) или малую диагональ и тангенс тупого угла ( tgβ ):

S =	1	d ₁ 2 · tg ( α /2)
2

S =	1	d ₂ 2 · tg ( β /2)
2

Окружность вписанная в ромб

Формулы определения радиуса круга вписанного в ромб:

1. Формула радиуса круга вписанного в ромб через высоту ромба:

2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:

3. Формула радиуса круга вписанного в ромб через площадь и синус угла:

4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:

5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:

6. Формула радиуса круга вписанного в ромб через две диагонали:

r =	d ₁ · d ₂
2√ d ₁ 2 + d ₂ 2

7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

[spoiler title=”источники:”]

Нахождение радиуса вписанной в ромб окружности

http://ru.onlinemschool.com/math/formula/rhombus/

[/spoiler]

Источник

Периметр ромба

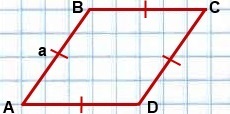
Ромб — это четырехугольник с равными сторонами.

Также его называют параллелограммом, у которого все ребра равны. При этом его противоположные углы тоже равны между собой. Если все углы равны 90 градусов, то это квадрат.

Периметр ромба – сумма длин всего его сторон или произведение любой его стороны на 4.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Способы нахождения

Рассмотрим все способы нахождения периметра этой фигуры.

По сторонам

Периметр ромба по сторонам

Источник: microexcel.ru

Если нам известны величины одного из его ребер, мы без проблем можем найти P по формуле:

(P;=;a+a+a+a;=;4times a,)

где a — это сторона ромба.

По двум диагоналям

Периметр ромба по двум диагоналям

Источник: microexcel.ru

Если наш ромб — не квадрат, то две его диагонали будут не равны между собой. Также в любом ромбе они пересекаются под углом 90 градусов, а в точке пересечения делятся пополам. Если обе из них нам известны, то можем вычислить периметр фигуры следующим образом:

(P=4timessqrt{left(d_1/2right)^2+left(d_2/2right)^2},)

где (d_1) и (d_2) — это диагонали четырехугольника.

Подобные вычисления получились исходя из свойств диагоналей равностороннего четырехугольника. Вместе со сторонами фигуры они образуют прямоугольный треугольник. По теореме Пифагора:

(a^2=left(d_1/2right)^2+left(d_2/2right)^2)

(a=sqrt{left(d_1/2right)^2+left(d_2/2right)^2}.)

По диагонали и углу

Периметр ромба по диагоналям и углу

Источник: math24.ru

Чтобы вычислить сумму всех ребер ромба данным способом, для начала нужно определить величину одной стороны:

если нам известен острый угол α: (a=frac{d_1}{sqrt{2+2cosalpha}};)
если известен тупой угол (β: a=frac{d_2}{sqrt{2-2cosbeta}}.)

Далее расчет P будет выглядеть следующим образом:

(P=frac{4d_1}{sqrt{2+2cosalpha}});
(P=frac{4d_2}{sqrt{2-2cosbeta}}.)

По площади и радиусу вписанной окружности

Периметр ромба по площади и радиусу вписанной окружности

Источник: ru.solverbook.com

По известной площади и радиусу вписанной окружности можно находить P, опираясь на формулу:

(P=frac{2S}r,)

где r — это радиус вписанной окружности.

По площади и синусу одного из углов

В этом случае формула расчета суммы всех сторон выглядит так:

(P=4timesfrac{sqrt S}{sqrt{sinalpha}},) либо

(P=4timesfrac{sqrt S}{sqrt{sinbeta}}.)

Через большую диагональ и половинный угол

Периметр ромба через большую диагональ и половинный угол

Источник: math24.ru

(P=frac{2d_1}{sqrt{cos(alpha/2)}}) или

(P=frac{2d_1}{sqrt{sin(beta/2)}}.)

Источник

Как найти периметр ромба, зная его сторону? Как найти периметр ромба по диагоналям? Как, если известен периметр ромба, найти его сторону?

Периметр ромба равен сумме длин всех его сторон.

Поскольку все стороны ромба равны, то формула периметра ромба

где a — длина стороны ромба.

Примеры.

1) Найти периметр ромба со стороной 7 см.

Решение:

По формуле P=4a имеем: P=4∙7=28 (см).

Ответ: 28 см.

2) Периметр ромба равен 36 см. Найти его сторону.

Решение:

По формуле P=4a имеем:

Значит, сторона ромба равна 9 (см).

Ответ: 9 см.

3) Найти периметр ромба, если его диагонали равны 12 см и 16 см.

Решение:

Чтобы найти периметр ромба, нужно знать его сторону.

В прошлый раз мы выводили формулу для нахождения стороны ромба через его диагонали:

$[{a = frac{1}{2}sqrt {d_1^2 + d_2^2} }]$

Отсюда приходим к формуле для нахождения периметра ромба по его диагоналям:

$[P = 4a = 4 cdot frac{1}{2}sqrt {d_1^2 + d_2^2} ]$

$[underline {P = 2sqrt {d_1^2 + d_2^2} } ]$

Значит, периметр ромба с диагоналями 12 см и 16 см равен

$[P = 2sqrt {{{12}^2} + {{16}^2}} = 2sqrt {144 + 256} = ]$

Ответ: 40 см.

Одна из формул для нахождения площади ромба S связывает радиус r вписанной в ромб окружности и его полупериметр p:

Выразим p через S и r:

$[p = frac{S}{r}]$

Так как P=2p, то приходим к формуле для нахождения периметра ромба через его площадь и радиус вписанной окружности

$[2p = frac{{2S}}{r}]$

$[underline {P = frac{{2S}}{r}} ]$

Источник

Ромб — это параллелограмм, у которого все стороны равны. При этом трапеция обладает всеми свойствами четырехугольника и параллелограмма. Поэтому запоминать надо свойства, которые характерны для ромба.

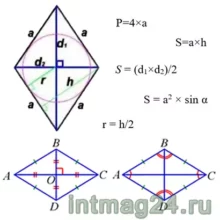
Свойства ромба:

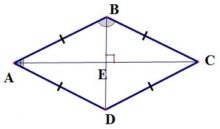
Противоположные углы равны. На рисунке: ∠BAC=∠DAC=∠BCA=∠DCA, ∠ABD=∠CBD=∠ADB=∠CDB.
Диагонали точкой пересечения делятся пополам. На рисунке: точка E.
Диагонали ромба пересекаются под прямым углом. На рисунке: AC⊥BD
Диагонали ромба являются биссектрисами его углов.

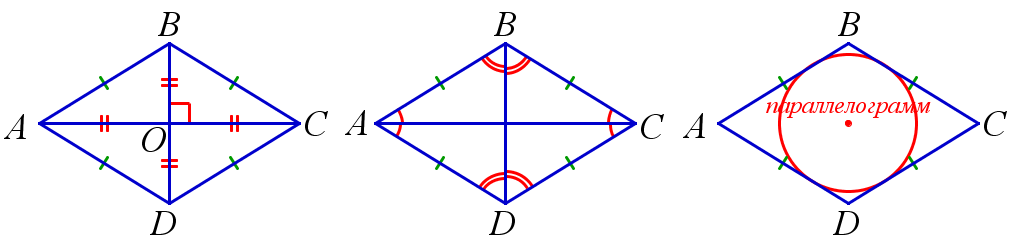
Признаки ромба:

Если диагонали четырёхугольника перпендикулярны и делятся точкой пересечения пополам, то этот четырёхугольник – ромб. На рисунке: AC⊥BD,AO=CO,BO=DO
Если диагонали четырёхугольника лежат на биссектрисах его углов, то этот четырёхугольник – ромб. На рисунке: ∠BAC=∠DAC,∠BCA=∠DCA∠ABD=∠CBD,∠ADB=∠CDB.
Если четырёхугольник — это параллелограмм и в него можно вписать окружность, то этот четырёхугольник – ромб. На рисунке: AB||CD,BC||AD,ABCD – описанный.

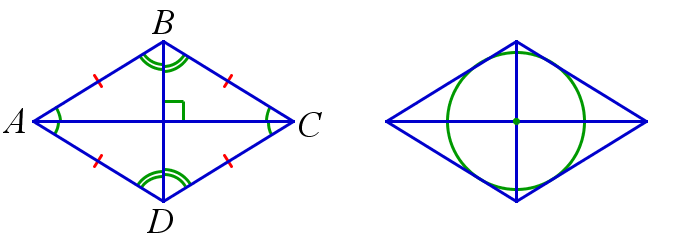
Ромб и окружность

В ромб можно вписать окружность. Центром этой окружности является точка пересечения диагоналей ромба.

Радиус окружности, вписанной в ромб, можно найти по формуле: или где: a — длина стороны, d₁, d₂ –диагонали.

Четырёхугольник можно описать окружностью, если сумма его противолежащих углов равна 180°. Таким образом, ромб, вписанный в окружность – это квадрат. Центр окружности совпадает с точкой пересечения диагоналей.

Основные формулы для ромба:

Периметр: Площадь по стороне и высоте: Площадь по диагоналям: Радиус окружности, вписанной в ромб: или Площадь по стороне и радиусу вписанной окружности:

Площадь по стороне и углу:

где a — длина стороны, d₁, d₂ –диагонали, P-периметр, S-площадь,
h -высота, проведенная к противоположной стороне
α — угол между сторонами ромба.

Источник

Формулы вычисления радиуса вписанной в ромб окружности
- Через диагонали и сторону
- Через диагонали
- Через сторону и угол
- Через высоту
Примеры задач