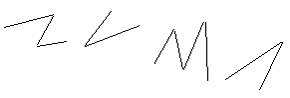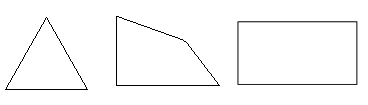Как найти периметр замкнутой ломаной

Ломаная линия

• Замкнутая и незамкнутая ломаная
• Самопересекающаяся ломаная
• Длина ломаной

Ломаная линия — это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего. При этом соседние (имеющие общую точку) отрезки не должны лежать на одной прямой.

Отрезки, из которых состоит ломаная, называются её звеньями, а концы этих отрезков — вершинами ломаной.

Построим ломаную из четырёх отрезков:

Отрезки  AB,  BC,  CD  и  DE  — это звенья ломаной. Точки  A,  B,  C,  D  и  E  — вершины ломаной. Обозначение ломаной линии составляют из букв, стоящих при её вершинах, называя их по порядку. Например, говорят или пишут: ломаная  ABCDE  или ломаная  EDCBA.

Замкнутая и незамкнутая ломаная

Незамкнутая ломаная — это ломаная линия, концы которой не совпадают друг с другом:

незамкнутая ломаная  ABCD.

Замкнутая ломаная — это ломаная линия, концы которой совпадают друг с другом:

замкнутая ломаная  ABC.

Самопересекающаяся ломаная

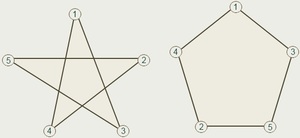
Замкнутые и незамкнутые ломаные линии могут быть самопересекающимися. Самопересекающаяся ломаная — это ломаная линия, звенья которой пересекают другу друга в одной или нескольких точках. Например:

точки  F,  T,  K  — точки самопересечения, то есть точки, в которых ломаная пересекает сама себя.

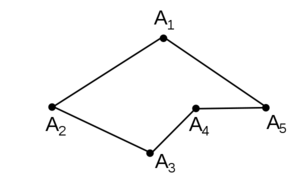
Замкнутая ломаная линия, у которой звенья не пересекаются между собой, называется многоугольником:

многоугольник  ABCDE.

Длина ломаной

Длина ломаной — это сумма длин всех её звеньев. Длина замкнутой ломаной, не имеющий самопересечений, то есть длина многоугольника, называется периметром.

Цели:

• уточнить понятия «длина ломаной», «периметр
  многоугольника», научить их находить;
• развивать вычислительные навыки, внимание,
  мышление, математическую речь;
• воспитывать любовь и бережное отношение к
  природе, к птицам.

Оборудование: опорные плакаты,
компьютерная презентация, карточки заданиями,
проволока.

ХОД УРОКА

1. Организационный момент

Долгожданный звонок
Начинается урок.

– Ребята, мы сегодня урок проведём в виде
путешествия в лес.

Мы в лес за наукой пойдём
Внимание, смекалку с собой возьмём.

Во время путешествия нам предстоит выполнить
интересные задания, познакомиться с новым
материалом. В конце урока узнаем, какими знаниями
мы вернулись.

2. Актуализация знаний

На опушке леса растут деревья,
А на деревьях задания.

Приложение 1, слайд 2.
Дан ряд чисел: 198, 202, 206, 210,

– Что у них общего?
– Какое число лишнее?
– В каком порядке расположены числа?
– Какое число самое маленькое?
– Какое число самое большое?
– Установите закономерность и определите
следующее число.
– Выразите число 214 в различных единицах счёта.
– Выразите 214 см в различных единицах измерения.

Приложение 1, слайд 3

– Расскажите всё, что вы знаете об этих
геометрических фигурах.

3. Постановка учебной задачи

– Посмотрите, что у меня в руках? (Проволока)
– Какую геометрическую фигуру она напоминает? (Прямую)
– Посмотрите, что я сделаю этой проволокой (сгибаю
в нескольких местах). Можно сказать, что это
прямая линия? (Нет)
– Вспомните, как называется такая
геометрическая фигура? (Ломаная линия).
– Как называют длину замкнутой ломаной линии? (Периметром)
– Значит, о чём мы будем говорить на уроке? (О
длине ломаной, о периметре.)
– Тема нашего урока «Длина ломаной, периметр».
Цель урока: научиться находить длину ломаной и
периметр.

4. «Открытие» детьми нового знания

Но вот и попали
Мы в сказочный лес
Лес этот полон
Прекрасных чудес.

Приложение 1, слайд 4 Поляна
«Открытий»

– Какая эта фигура?
– Назовите признаки ломаной линии. (Ломаная
состоит из отрезков, конец одного отрезка
является началом другого, 2 соседних отрезка не
лежат на одной прямой)
– Отрезки ломаной линии называют звеньями
ломаной, место, где соединяются 2 звена,
называется вершиной.
– Покажите звенья и вершины ломаной линии. (1
ученик выходит к доске и показывает)

Приложение 1, слайд 5

– Какие геометрические фигуры вы видите?
– Какая из ломаных имеет больше всего звеньев?
– Какая – меньше звеньев?
– Какая из ломаных самая длинная? (Ответы
детей)
– Как доказать? (Нужно измерить длину ломаной).
– Как измерить длину ломаной? (Измерить длину
каждого звена и результаты сложить).
– Ребята, у вас на партах карточки с рисунками
ломаных линий. Измерьте длину каждого звена и
найдите длину ломаной. Работаем в парах.
– Проверим. Какая длина 1 ломаной линии? 2?
– Какая самая длинная?
– Как вы нашли длину ломаной? Сделаем вывод.
Вывод. Чтобы найти длину ломаной нужно
длину её звеньев сложить.
– Значит, что называют длиной ломаной? (Длиной
ломаной называют сумму длин её звеньев.)

Приложение 1, слайд 6

– Можем ли мы эти линии назвать ломаными? (Да)
– Чем они отличаются от предыдущих? (Это
замкнутые ломаные линии).
– Можем найти длины этих ломаных?
– Что нужно для этого сделать? (Измерить длину
каждого звена и найти сумму длин всех звеньев
ломаной).
– Измерьте длину каждого звена и найдите длину
замкнутой ломаной лини. Продолжаем работу в
парах.
– Проверим: длина 1 замкнутой линии – …, 2 – ….
– Какие фигуры образуют замкнутые ломаные линии?
(Многоугольники)
– Находя длину замкнутой ломаной, вы находили
сумму длин всех сторон многоугольника.
– Вспомните, как называют сумму длин сторон
многоугольника? (Периметром)
Сумму длин всех сторон многоугольника
называют периметром.
– Как найти периметр многоугольника? (Чтобы
найти периметр многоугольника нужно длину всех
сторон сложить.)

5. Физминутка (под музыку Е. Железнова
«Игровая гимнастика».)

Приложение 1, слайд 7

Поляна «Отдыхай-ка»

Утром на лесной опушке
Собираются зверюшки.
Все приучены к порядку
Дружно делают зарядку.
1-2-3 …
Привыкайте все к порядку:
Начинайте день с зарядки!

– Почему нужно делать зарядку?

6. Первичное закрепление.

Приложение 1, слайд 8

Поляна «Закрепляй-ка»

1) №2 с. 16

– Что вы знаете о сторонах прямоугольника? (Противоположные
стороны прямоугольника равны).
– Чтобы найти его периметр, длины каких сторон
достаточно знать? (Нужно измерить длину и
ширину).
– Измерьте длину и ширину прямоугольника и
найдите Р .

2) №1 с. 16.

– Прочитайте задачу.
– Что нужно сделать?
– Как найти длину ломаной?
– Эту задачу вы решите дома. Запишите в дневник.

Приложение 1, слайд 9

Поляна «Применяй-ка»

– Где в жизни могут понадобиться знания
находить Р? (Когда будем делать рамку для фото,
строить забор, прибивать плинтус…)
– А длину ломаной? (Когда будем вычислять путь
от дома до школы …)
– Мы с вами решили сделать кормушку, спилили
доску-основу длиной 6 дм шириной 4дм. По краям
нужно прибить узкую рейку. Какой длины рейка
понадобится? (20 см)

– Кормушку мы повесим во дворе Лесной школы.
Птицы до нашей кормушки долетят в том случае,
если мы поможем « ученикам» Лесной школы.

Приложение 1, слайд 10.
Рисунок «Лесная школа», чертёж задачи.

1) составим задачу
2) составим схему к задаче
3) решим задачу (1 ученик решает у доски с
комментированием , он в роли учителя)

– Молодцы! Вы помогли и ученикам Лесной школы, и
птицам.

Приложение 1, слайд 11.
Рисунок кормушки.

Здесь на этом суку
Кормушку повесим
У птиц на виду .
Чтоб были сыты
Они лютой зимой
И с пользой ответили
Лесу весной.

– Какую пользу они приносят?
– Поэтому мы должны им помочь?
– В классе мы объявили операцию «Синица».
Поднимите руку, кто уже сделал кормушку?

7. Проверочная работа по вариантам

Приложение 1, слайд 12.
Поляна «Проверяй-ка»

Приложение 1, слайд 13.
Проверьте:

1 в
.                 
2 в.
20
см               
20 см
27
см               
22 см
24
см                
29 см

Самопроверка и самооценивание работ.

8. Включение в систему знаний и повторение

Приложение 1, слайд 14.
Поляна «Объясняй-ка»

1) № 6, с.17 – с объяснением
– Что нужно знать, чтобы дополнить чертёж? (Что
здесь целое, что_– часть).
2) № 7, с.17 – самостоятельно. Проверка.
3) № 8, с.17 – «цепочкой»

9. Рефлекция деятельности (итог урока)

– Вот и вышли мы из леса. Какие новые знания мы
получили? (Мы научились находить длину ломаной
и периметр).
– Как найти длину ломаной? Периметр?
– Чем мы будем заниматься на следующих уроках? (Находить
длину стороны многоугольника).

Как поступить
в Онлайн-школу и получить аттестат?

Подробно расскажем о том, как перевестись на дистанционный формат обучения, как устроены онлайн-уроки и учебный процесс, как улучшить успеваемость и повысить мотивацию!

Нажимая на кнопку, я соглашаюсь на обработку

персональных данных

Конспект урока: Длина ломаной. Периметр многоугольника

Планиметрия

Длина ломаной. Периметр многоугольника

Цели урока

• научимся находить длину ломаной и периметр многоугольника

---

Как начертить ломаную? 

Начертите три ломаные линии. 

Красным цветом – ломаную состоящую из 3 звеньев. 

Синим цветом – ломаную состоящую из 2 звеньев.

Зеленым – ломаную из 4 звеньев. 

Как определить какая из этих ломаных длиннее?

---

Вспомним! 

Ломаная линия
 – это геометрическая фигура, которая состоит из нескольких отрезков, последовательно соединенных своими концами.

Ломаная линия может состоять из очень многих звеньев. Может быть замкнутой и не замкнутой (рис. 1).

Рис. 1. Замкнутая и незамкнутая ломаные

Замкнутая ломаная линия называется еще многоугольником. 
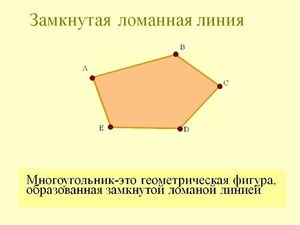
Многоугольник
– это геометрическая фигура, которая состоит из замкнутой ломаной линии.

Многоугольники могут быть разными. Их названия зависят от количества углов многоугольника.

Для того, чтобы найти длину ломаной, нужно сложить длину всех звеньев, из которых состоит ломаная.

---

Начертите ломаную линию, длина которой равна 15 см.

---

Существует второй способ нахождения длины ломаной. 

Отложим на прямой один за другим отрезки, равные по длине звеньям ломаной. Это можно сделать с помощью циркуля или нитки. Накладываем циркуль на первый отрезок, переносим его на прямую.

---

Найдите длину ломаной. Как по-другому назвать фигуру? Как называется длина всех ее сторон?

---

Периметр
– это сумма длин всех сторон многоугольника. Кратко слово «периметр» записывается латинской буквой «пэ» – Р.

Способы нахождения периметра многоугольника
 

1 способ

Измерить с помощью линейки длину каждой стороны фигуры. Сложить значения длин.
 

P= 6 см + 6 см + 3 см + 3 см = 18 см
 

2 способ

С помощью циркуля на прямой отложим один за другим отрезки равные по длине сторонам четырехугольника. Далее с помощью линейки узнаем длину получившегося отрезка.

---

Упражнение 1

Начертите замкнутую линию со сторонами 4 см, 4 см, 2 см, 2 см. Найдите ее периметр.

---

Упражнение 2

Начертите ломаную из 3 звеньев. Длина каждого звена равна 2 см. Найдите длину ломаной.

---

Упражнение 3

Начертите четырехугольник и найдите его периметр, если стороны равны 5 см, 3 см, 4 см, 3 см.

---

Покажите на пальцах, какую отметку за урок вы себе поставите. Отметьте свой вариант ниже.

---

Ответы

Упражнение 1

Упражнение 2

2+2+2=6 (см)

Ответ : 6 см длина ломаной.

Упражнение 3

(рисунок может быть выполнен иначе)

P = 5+3+4+3 = 15 (cм)

Ответ: 15 см периметр четырехугольника.

---

Предыдущий урок

Многоугольники. Прямоугольник. Квадрат

Планиметрия

Следующий урок

Числовое выражение.

Числовые и буквенные выражения

Зарегистрируйся, чтобы присоединиться к обсуждению урока

Добавьте свой отзыв об уроке, войдя на платфому или зарегистрировавшись.

Ломаная линия

Ломаная линия — это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего. При этом соседние (имеющие общую точку) отрезки не должны лежать на одной прямой.

Отрезки, из которых состоит ломаная, называются её звеньями, а концы этих отрезков — вершинами ломаной.

Построим ломаную из четырёх отрезков:

Отрезки AB, BC, CD и DE — это звенья ломаной. Точки A, B, C, D и E — вершины ломаной. Обозначение ломаной линии составляют из букв, стоящих при её вершинах, называя их по порядку. Например, говорят или пишут: ломаная ABCDE или ломаная EDCBA .

Замкнутая и незамкнутая ломаная

Незамкнутая ломаная — это ломаная линия, концы которой не совпадают друг с другом:

незамкнутая ломаная ABCD.

Замкнутая ломаная — это ломаная линия, концы которой совпадают друг с другом:

замкнутая ломаная ABC.

Самопересекающаяся ломаная

Замкнутые и незамкнутые ломаные линии могут быть самопересекающимися. Самопересекающаяся ломаная — это ломаная линия, звенья которой пересекают другу друга в одной или нескольких точках. Например:

точки F, T, K — точки самопересечения, то есть точки, в которых ломаная пересекает сама себя.

Длина ломаной

Длина ломаной — это сумма длин всех её звеньев. Длина замкнутой ломаной, не имеющий самопересечений, то есть длина многоугольника, называется периметром.

Пример 1. Найти длину ломаной из 3 звеньев.

Решение: Для нахождения длины ломаной, состоящей из трёх звеньев, надо сложить длины всех её звеньев. Длина ломаной ABCD будет равна:

AB + BC + CD = 4 см + 3 см + 2 см = 9 см.

Ответ: Длина ломаной ABCD равна 9 см.

Пример 2. Найти длину замкнутой ломаной.

Решение: Найдём периметр замкнутой ломаной, сложив длины всех её звеньев:

AB + BC + CD + DA =
3 см + 5 см + 4 см + 5 см = 17 см.

Замкнутые самопересекающиеся ломаные

Александр Блинков, Александр Грибалко
«Квантик» №11, 2019

В этой статье пойдёт речь о ломаных линиях на плоскости. Для того чтобы изобразить ломаную, достаточно выбрать несколько точек (не меньше трёх), занумеровать их в каком-нибудь порядке, после чего последовательно соединить отрезками точки с соседними номерами. Выбранные точки называются вершинами ломаной, а отрезки — её звеньями (на рисунке 1 — трёхзвенная ломаная с четырьмя вершинами).

Если хотя бы два звена ломаной пересекаются (в своих внутренних точках), её называют самопересекающейся (на рисунке 2 — четырёхзвенная самопересекающаяся ломаная).

И наконец, если первая и последняя вершины ломаной совпадают, её называют замкнутой. В такой ломаной количество вершин совпадает с количеством звеньев (на рисунке 3 изображена пятизвенная замкнутая ломаная).

Нас будут интересовать замкнутые самопересекающиеся ломаные.

Начнём с задачи, предложенной А. Пешниным (её частные случаи были использованы на XXV турнире математических боёв имени А. П. Савина).

Задача 1

Сколько вершин может быть у замкнутой ломаной, которая каждое своё звено пересекает ровно два раза?

Очевидно, что трёхзвенная замкнутая ломаная не может быть самопересекающейся. Замкнутая ломаная с четырьмя вершинами также не удовлетворяет условию задачи, так как соседние звенья пересечься не могут, а для каждого звена есть только одно не соседнее. Пример пятизвенной ломаной хорошо известен — это пятиконечная звезда (см. рис. 4, а, где вершины ломаной делят окружность на пять равных частей). Идея использовать окружность тут не обязательна, но удобна и пригодится в дальнейшем.

Этот пример подсказывает, что аналогичным образом можно построить любую ломаную, удовлетворяющую условию, с нечётным количеством звеньев, большим трёх. Достаточно поставить на окружности требуемое количество вершин и последовательно соединить их через одну. Например, на рисунке 4, б — искомая ломаная с девятью звеньями.

Осталось разобраться с ломаными, у которых чётное количество звеньев, начиная с шести.

Искомой шестизвенной ломаной не существует, но доказывать это мы умеем только перебором всех случаев, который не очень интересен.

Для восьми звеньев существует красивый пример (рис. 5, а). Аналогично можно построить ломаную, удовлетворяющую условию, с любым чётным количеством звеньев, большим восьми. Как это делается, понятно из примеров для десяти и двенадцати звеньев, показанных на рисунках 5, б и 5, в. Сначала мы отмечаем на окружности точки, которых на две меньше, чем нужно, и соединяем их через одну. Так как точек чётное количество, получатся две замкнутые ломаные, все звенья которых пересекаются с другой ломаной в двух точках. После этого удаляем по одному звену в каждой ломаной и соединяем ломаные в одну, используя ещё две вершины, расположенные внутри окружности.

Есть и более простой способ. Воспользуемся тем, что любое чётное число, большее восьми, можно представить в виде суммы двух нечётных слагаемых, каждое из которых не меньше пяти.

Покажем, например, как построить двенадцатизвенную ломаную, удовлетворяющую условию. Изобразим две окружности, которые касаются друг друга внешним образом в некоторой точке. В одной из окружностей построим уже указанным способом пятизвенную ломаную, а в другой — семизвенную, причём точка касания должна быть их общей вершиной. А теперь эту точку «раздвоим» (рис. 6, результат раздвоения — вершины с номерами 1 и 6).

Аналогично строятся все искомые ломаные, у которых количество звеньев чётное и больше восьми.

Возникает вопрос: почему мы начали с двух точек пересечения звеньев, а не с одной, что, казалось бы, более естественно?

Дело в том, что такой порядок более логичен, так как решение следующей задачи будет во многом опираться на решение рассмотренной.

Задача 2

Сколько вершин может быть у замкнутой ломаной, которая каждое своё звено пересекает ровно один раз?

Сразу заметим, что в этом случае звенья ломаной должны разбиваться на непересекающиеся пары, поэтому у искомых ломаных — чётное количество звеньев. Легко проверить, что замкнутая ломаная из четырёх звеньев условию не удовлетворяет.

Пример искомой ломаной из шести звеньев можно построить, исходя из следующих соображений: помимо того, что не могут пересекаться соседние звенья, не могут пересекаться и звенья, стоящие через одно. Действительно, в этом случае образуется треугольник (рис. 7, а), в который можно будет только «войти», если пересечь среднее звено, но нельзя будет «выйти». Поэтому надо пересекать первое звено с четвёртым, второе — с пятым, а третье — с шестым (рис. 7, б).

Пример искомой ломаной из восьми звеньев читателю предлагается построить самостоятельно (см. задачи в конце статьи). А вот пример десятизвенной ломаной можно получить, обратившись к задаче 1. Действительно, рассмотрим пример замкнутой пятизвенной ломаной, которая каждое своё звено пересекает два раза (рис. 4). «Сломаем» каждое звено между двумя точками пересечения и получим искомый пример (рис. 8). Аналогично, рассмотрев семизвенную ломаную из задачи 1, можно получить решение для ломаной с четырнадцатью звеньями; пример восьмизвенной ломаной из задачи 1 помогает получить решение для ломаной из шестнадцати звеньев, и т. д.

Этот приём не годится только для построения двенадцатизвенной ломаной, так как нет шестизвенной ломаной, которая каждое своё звено пересекает два раза. Но в этом случае можно использовать другую идею решения задачи 1: «раздвоение». Построим две ломаные из рис. 7, б с общей вершиной и «раздвоим» её (рис. 9, результат раздвоения — вершины с номерами 6 и 12). Понятно, что идея «раздвоения» вершин более универсальна. В том числе и потому, что позволяет комбинировать ломаные с разным количеством звеньев.

Надеемся, что идеи и приёмы, описанные выше, помогут при решении других задач.

Упражнения и задачи для самостоятельного решения

1. Может ли прямая, не содержащая вершин замкнутой девятизвенной ломаной, пересечь каждое её звено?

2. (В. Произволов) Замкнутая ломаная такова, что каждые два её не соседних звена пересекаются. Докажите, что у этой ломаной нечётное количество звеньев.

3. Существует ли пятнадцатизвенная ломаная, пересекающая каждое своё звено ровно три раза?

4. Постройте восьмизвенную замкнутую ломаную, которая каждое своё звено пересекает один раз.

5. (Д. Калинин, вариация фольклора) Маша нарисовала замкнутую семизвенную ломаную. Для каждого звена она записала, со сколькими звеньями оно пересекается во внутренних точках. Могла ли она записать в каком-то порядке числа 1, 2, 3, 4, 3, 2, 1?

6. Какое наибольшее количество точек самопересечения может иметь замкнутая семизвенная ломаная?

7. (Н. Васильев) Рассматриваются всевозможные шестизвенные замкнутые ломаные, все вершины которых лежат на окружности.

1. Нарисуйте ломаную, которая имеет наибольшее возможное количество точек самопересечения.
2. Докажите, что нельзя нарисовать ломаную с большим количеством самопересечений.

Как выглядит замкнутая ломаная линия

Ломаной линией в геометрии принято называть геометрическую фигуру, которая состоит из двух или нескольких отрезков. Конец одного отрезка является началом другого. Обязательное условие, которому подчиняется любая ломаная, — соседние отрезки не должны располагаться на одной прямой.

Эти геометрические фигуры находят самое широкое применение в разных областях науки и практики:

1. Картография — для построения изображений улиц и схем маршрутов.
2. Архитектура — очертания зданий и строений.
3. Ландшафтный дизайн — декоративное оформление и расположение тропинок.
4. Химия — молекулярная структура сложных полимерных соединений.
5. Медицина — мониторы для контроля функционального состояния органов и систем.

Типы ломаных линий

Рассматриваемые геометрические фигуры могут быть выстроены самыми разнообразными способами — они могут быть незамкнутыми и замкнутыми, пересекающимися и непересекающимися.

Замкнутая ломаная соответствует определенной геометрической фигуре — многоугольнику.

Если отрезки одной такой фигуры имеют точки пересечения друг с другом — эта линия называется самопересекающейся.

Всего существует 4 типа подобных линий по своей структуре:

1. Замкнутые, которые не имеют пересечений.
2. Незамкнутые, которые не имеют пересечений.
3. Незамкнутые самопересекающиеся.
4. Замкнутые, имеющие самопересечения.

Разновидностью такой геометрической фигуры может считаться зигзаг, у которого последовательные отрезки образуют прямой угол и параллельны друг другу через один. Зигзагами широко пользуются в обиходе — в портновском мастерстве, декоративном искусстве, оформлении предметов обихода.

Особенности замкнутых линий

Рассмотрим подробнее составляющие части этой геометрической фигуры.

1. Один отрезок из тех, что составляют описываемую фигуру, называется ее звеном. Ломаной может считаться такая линия, которую составляют как минимум два отрезка — звена. Если звено одно — это просто единичный отрезок.
2. Существует также понятие вершины ломаной. Этим термином принято называть точку, в которой соединяются концы двух звеньев. Такие точки в геометрии принято обозначать с помощью заглавных латинских букв. Сама ломаная называется сочетанием обозначений этих вершин. Например, названием такой линии может послужить сочетание ABCDEF.
3. Если концы крайних звеньев этого геометрического объекта соединяются в одной точке, такая линия называется замкнутой.
4. Ломаная линия может пересекать саму себя.
5. Конечные вершины такой фигуры в геометрии принято называть черными точками.

Как уже было сказано выше, эта разновидность линий может иметь самопересечения. Наиболее популярным примером замкнутой линии, имеющей самопересечения, является пятиконечная звезда.

Многоугольник как разновидность замкнутой ломаной

Разновидностью описываемой геометрической фигуры является многоугольник. Точками в многоугольнике являются его вершины, а отрезки называются сторонами.

1. Если вершины принадлежат одной и той же стороне многоугольника — они носят название смежных.
2. Если отрезок соединяет две любых вершины, не являющиеся смежными, он называется диагональю.
3. Если у многоугольника имеется n вершин — он называется n-угольником. У такой фигуры имеется количество сторон, равное n.
4. Такая ломаная делит плоскость на 2 части — внешнюю и внутреннюю.
5. Если точки многоугольника лежат по одну сторону от прямой и проходят через 2 соседние вершины — его принято называть выпуклым.
6. Угол выпуклого многоугольника при данной вершине — это угол, который образован двумя его сторонами, для которых эта вершина является общей.
7. Внешний угол выпуклого многоугольника при определенной вершине — это угол, смежный с внутренним углом многоугольника при этой же самой вершине.

Примерами многоугольников являются четырехугольники, треугольники, пятиугольники. Рассмотрим подробнее отличительные черты этих фигур.

Треугольник — это геометрическая фигура, которая состоит из трех точек, расположенных не на одной прямой. Эти точки попарно соединяются между собой отрезками.

Четырехугольником в геометрии называется фигура, которая имеет четыре угла и четыре стороны. Четырехугольники встречаются самые разнообразные — это могут быть трапеции, квадраты, параллелограммы, ромбы.

У трапеции параллельны две стороны, которые называются основаниями. Остальные две стороны не параллельны. У параллелограмма между собой параллельны две противоположные стороны.

Отличительной чертой прямоугольника является то, что все его углы прямые. У квадрата являются равными все четыре стороны. Кроме того, все углы у квадрата являются прямыми.

Если у многоугольника все стороны и углы равны, он называется правильным. Такой многоугольник всегда будет выпуклым.

[spoiler title=”источники:”]

http://elementy.ru/nauchno-populyarnaya_biblioteka/435285/Zamknutye_samoperesekayushchiesya_lomanye

http://liveposts.ru/articles/education-articles/matematika/kak-vyglyadit-zamknutaya-lomanaya-liniya

[/spoiler]

МБОУ лицей № 1 им. академика Б.Н. Петрова

Тема урока:

«Ломаная линия. Длина ломаной линии. Периметр»

Цели урока:

Образовательные:

1. Создать условия для формирования представления о длине ломаной, периметре многоугольника, способность в простейших случаях к их нахождению на основе измерений и вычислений.

2. Проверить уровень усвоения изученного материала.

Развивающие:

1. Развивать вычислительные навыки и математическую речь.

2. Развивать умение формулировать проблемы и предлагать пути их решения, самостоятельность при выполнении практических задач.

3. Развивать умения осуществлять самоконтроль, самокоррекцию учебной деятельности.

4. Развивать коммуникативные качества, монологическую и диалогическую речь.

Воспитательные:

1. Воспитывать познавательный интерес к предмету.

2. Воспитывать навыки умственного труда.

3. Воспитывать уважительное отношение друг к другу, работая в парах и коллективно.

Планируемые результаты

Личностные результаты:

– положительное отношение к учению;

– учебно-познавательный интерес к новому учебному материалу и способам решения новых задач;

– способность к оценке своей деятельности;

– уважение к собеседнику.

Метапредметные результаты:

Регулятивные:

– умение определять и формулировать цель на уроке с помощью учителя;

– проговаривание последовательности действий на уроке;

– планирование своего действия в соответствии с поставленной задачей;

– внесение необходимых корректив в действие после его завершения на основе его оценки и учёта характера сделанных ошибок;

– оценивание правильности выполнения действия на уровне адекватной ретроспективной оценки.

Познавательные:

– умение ориентироваться в своей системе знаний, отличать новое от уже известного;

– умение с помощью учителя добывать новые знания;

– осуществление синтеза как составление целого из частей;

– нахождение ответов на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке.

Коммуникативные:

– умение с достаточной полнотой и точностью выражать свои мысли,

– готовность слушать и понимать речь других;

– умение работать в паре;

– формулирование своего мнения и позиции.

Предметные результаты:

– осваивание опыта самостоятельной математической деятельности по получению нового знания, его преобразованию и применению для решения учебно-познавательных и учебно-практических задач;

– использование приобретённые математические знания для описания и объяснения окружающих предметов, процессов, явлений;

– умение решать текстовые задачи;

– приобретение начального опыта применения математических знаний для решения учебно-познавательных и учебно-практических задач.

Оборудование: доска, компьютер, интерактивная доска, карточки, раздаточный материал, учебник математики (2 часть), автор Л.Г. Петерсон М. “Ювента”, 2006 г.

Ход урока.

1. Мотивация к учебной деятельности.

(Слайд 1)

– Сегодняшний урок я хочу начать словами французского философа Ж.Ж. Руссо (1712–1778 гг.): «Вы талантливые дети! Когда-нибудь вы сами приятно поразитесь, какие вы умные, как много и хорошо умеете, если будете постоянно работать над собой, ставить новые цели и стремиться к их достижению…» Я желаю вам уже сегодня на уроке убедиться в словах Ж.Ж. Руссо.

– Вы готовы к работе? Тогда в путь.

2. Актуализация знаний.

– Сегодня на уроке, ребята, вас ожидает много интересных заданий, новых открытий, а помощниками вам будут: внимание, находчивость, смекалка. Итак, проверим, насколько вы внимательны.

(Слайд 2, 3, 4)

–

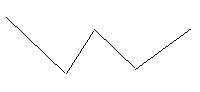
– Сколько фигур изображено? (5)

– Какая из них лишняя? Почему?

– Нарисуйте их по памяти.

– Проверим.

– Молодцы! Теперь, когда мы знаем, что все мы внимательные, продолжаем наш урок.

3. Постановка темы и цели урока.

(Слайд 5)

– Найти на чертеже прямую линию и назвать ее свойства. (Прямая не имеет начала и конца – она бесконечна, поэтому ее нельзя измерить).

– Без конца и края, линия прямая!

Хоть сто лет по ней иди,

Не найдешь конца пути!

– Покажите на чертеже отрезок. Назовите его свойства. (Отрезок – часть прямой, ограниченный двумя точками. У отрезка есть начало и конец, поэтому его можно измерить с помощью линейки).

– Покажите на чертеже луч. Что называется лучом? Назовите его свойства. (Если отметить точку и из нее провести часть прямой, то получится изображение луча. Точка из которой проведена часть прямой называется началом луча. Конца у луча нет поэтому его измерить нельзя).

– Вспомните, как называется страна, в которой живут прямая, луч, отрезок и фигуры, которые мы изображали по памяти? (Геометрия).

– Верно. Сегодня мы продолжим путешествие по этой стране – Геометрии.

– Посмотрите, что у меня в руках? (Проволока).

– Какую геометрическую фигуру она напоминает? (Прямую).

– Посмотрите, что я сделаю с этой проволокой. (Согнуть в нескольких местах).

– Можно ли теперь сказать, что это прямая? (Нет).

– Вспомните, как называется такая геометрическая фигура? (Ломаная линия).

– Скажите, чему будет посвящён сегодняшний урок?

– Сегодня на уроке мы попытаемся выявить признаки и свойства ломаной линии, научимся находить её длину, а так же вспомним, что такое периметр фигуры и как его находить.

4. «Открытие» нового знания.

– У вас на партах лежат куски проволоки. Давайте сделаем модели ломаных линий.

– Что можно сказать об этой ломаной линии. Из скольких частей она состоит. (Из 4)

– Как называется каждая часть ломаной? (Отрезок или звено).

– Найдите и покажите вершины ломаной. Сколько их? (3).

(Слайд 6)

– Верно. Каждая ломаная состоит из звеньев, которые не лежат на одной прямой. Конец одного отрезка является началом второго отрезка, конец второго отрезка – началом третьего. Места соединения отрезков называются вершинами ломаной, а отрезки – звеньями ломаной.

– У вас на партах лежат разноцветные отрезки. Постройте из них ломаные линии.

(Работа по вариантам)

I вариант II вариант

(2 учащихся строят такие же линии на магнитной доске)

– Какая ломаная имеет больше звеньев? Сколько их?

– А во II ломаной сколько звеньев?

– Какая ломаная самая длинная? Как доказать? (Нужно измерить длину).

– Как найти длину ломаной? (Измерить длины линий и результаты сложить).

(Слайд 7)

– Измерьте длину своей ломаной и результаты запишите в тетради.

(2 учащихся выполняют это у доски)

5+7+6+8=26 (см) 4+7+3+5+6=25 (см)

– Какая же ломаная получилась длиннее? (I)

– I ломаная состоит из 4 звеньев, а II из 5, но I оказалась длиннее. Какой вывод можно сделать? (Длина ломаной не зависит от количества звеньев, а от их длины).

– Вы сейчас пользовались линейками. А знаете ли вы сколько ей лет?

(Учащиеся рассказывают историю линейки)

Линейке исполнилось 224 года. Однако линейкой пользовались и в более ранние времена. В Средневековье, например, немецкие монахи для разметки линий на пергаменте (так называлась бумага) пользовались тонкими свинцовыми пластинками. А в ряде стран Европы, в том числе и в Древней Руси, для этих целей применялись железные прутья. Их называли шильцами. В разных странах люди измеряли одно и тоже расстояние по-разному. Это было очень неудобно . Наконец, во Франции в 1789 году решено было ввести единую систему мер. В Париже изготовили платиновые линейки с делениями, которые стали образцами мерок для всего мира. По их образцу изготовили деревянные линейки. В Россию линейка попала после войны 1812 года в качестве трофея.

– Итак, что же нужно сделать, что бы найти длину ломаной линии?

– А где мы можем в окружающем нас мире увидеть ломаные линии?

– Давайте закроем глаза и вспомним звездное небо.

(Слайды 8, 9, 10, 11).

– Можем ли мы созвездие Цефея или сам ковш Большой Медведицы назвать ломаными? (Да)

– Чем они отличаются от предыдущих? (Это замкнутые ломаные).

– Можем ли мы найти длины этих ломаных?

– Что нужно для этого сделать?

– Замкнутые линии образуют многоугольники. Находя длину замкнутой ломаной, вы находите сумму длин сторон многоугольника. Вспомните, как называется сумма длин сторон многоугольника? (Периметр).

– Что такое периметр многоугольника?

(Слайд 12)

– Найдите длину замкнутой ломаной линии или периметр многоугольников лежащих у вас на парте.

(Дети работают в парах)

Физкультминутка

5. Первичное закрепление.

– Используя полученные знания, мы решим некоторые задания. Работа по учебнику стр. 16 № 1

(Учащиеся выполняют задание).

– Выполним задание №1 на карточке:

Найдите длину ломаной, I звено которой 14 см., II звено на 7 см. длиннее, а II столько сколько I и II вместе.

– Прочитаем эту задачу.

– Что известно в задаче?

– Что нужно узнать?

– Длина ломаной – это целое или часть? (Целое).

– А на сколько частей оно разделено? (На 3).

– Можем ли мы сразу узнать это целое? (Нет, не знаем вторую и третью части).

– Значит, найдем сначала их.

– К доске пойдет … решать эту задачу. (Один ученик выполняет задание у доски, а остальные в тетрадях)

– Выполним задание №2:

Начертите ломаную состоящую из 3 одинаковых частей, длина которой 15 см.

– Чему будет равно каждое звено ломаной (5 см.)

– Начертите эту ломаную в тетради.

6.Самостоятельная работа по новой теме.

– Самостоятельно выполните задание №3

Длина ломаной линии 70 см, 1 звено 32 см, 2 звено на 13 см короче. Чему равно 3 звено?

(Учащиеся самостоятельно выполняют задание в тетради)

– Теперь поменяйтесь тетрадями и проверьте работу своего соседа.

(На доске записано решение)

7. Рефлексия учебной деятельности.

– Какую цель мы ставили в начале урока? Достигли мы её?

– Как найти длину ломаной?

– Что такое периметр?

(Слайд 13)

– Как вы думаете, зачем мы учимся находить длину ломаной линии, периметр, пригодится ли нам это в жизни? Для чего?

– А сейчас напишем графический диктант: отступите от предыдущей работы 4 клеточки вниз и в нижнем левом углу 5 клеточки поставьте точку, 2 клеточки вправо, 3 клеточки вверх – поставьте точку, 2 клеточки вправо, 4 клеточки вниз – поставьте точку, 3 клеточки вправо, 3 клеточки вверх поставьте точку, 4 клеточки вправо, 2 клеточки вниз – поставьте точку, 4 клеточки вправо, 3 клеточки вверх- поставьте точку, 3 клеточки вправо, 2 клеточки вниз – поставьте точку

– Нарисуйте в тетради ломаную линию, соединив точки, в соответствии со схемой вашего настроения, если вы хорошо поработали на уроке – зелёным цветом, если вам не всё удалось и нужно ещё поработать над данной темой – красным.

– У кого зелёная ломаная?

– У кого красная? Что на уроке не получалось?

– Вы преодолели трудность? Что помогло вам её преодолеть?

– Спасибо за работу.

Технологическая карта урока

Этапы урока

Формируемые УУД

Деятельность учителя

Деятельность обучающегося

1. Мотивация учебной деятельности

Регулятивные УУД:

планировать своё действие в соответствии с поставленной задачей;

Личностные УУД:

положительное отношение к учению;

Обеспечивает мотивацию к учебной деятельности. Проверяет готовность обучающихся к уроку.

Проверяют свою готовность к уроку.

2.Актуализация знаний

Личностные УУД:

способность к оценке своей деятельности;

Регулятивные УУД:

вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок

Проверяет у обучающихся знание геометрического материала.

Повторяют геометрический материал: сравнивают прямую, луч, отрезок, описывают их свойства.

3. Постановка темы и цели урока

Регулятивные УУД:

уметь определять и формулировать цель на уроке с помощью учителя;

Озвучивает цель урока

Определяют цель урока

4. «Открытие» нового знания

Личностные УУД:

учебно-познавательный интерес к новому учебному материалу и способам решения новых задач;

Познавательные УУД:

с помощью учителя добывать новые знания;

Коммуникативные УУД:

учиться работать в паре;

Создаёт условия для формирования представления о длине ломаной, периметре многоугольника, способность в простейших случаях к их нахождению на основе измерений и вычислений.

Строят с помощью линейки ломаные линии, измеряют с помощью линейки звенья ломаной. Строят общий способ нахождения длины ломаной и периметра многоугольника, применяют его для решения задач.

5. Первичное закрепление

Познавательные УУД:

уметь ориентироваться в своей системе знаний, отличать новое от уже известного;

Проверяет уровень усвоения изученного материала.

Применяют знания и способы действий в поисковых ситуациях.

6.Самостоятельная работа по новой теме

Познавательные УУД:

находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке.

Регулятивные УУД:

оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки

Контролирует выполнение работы. Организует взаимопроверку.

Применяют изученные способы действий для решения задач в типовых ситуациях.

Осуществляют взаимопроверку.

7. Рефлексия учебной деятельности

Личностные УУД:

способность к оценке своей деятельности;

Коммуникативные УУД:

формулировать своё мнение и позицию.

Организует беседу по уточнению и конкретизации первичных знаний, оценочные высказывания обучающихся.

Называют основные позиции нового материала, и как они их усвоили (что получилось, что не получилось и почему)